相似三角形判定1(灵)
图片预览

文档简介
(共13张PPT)
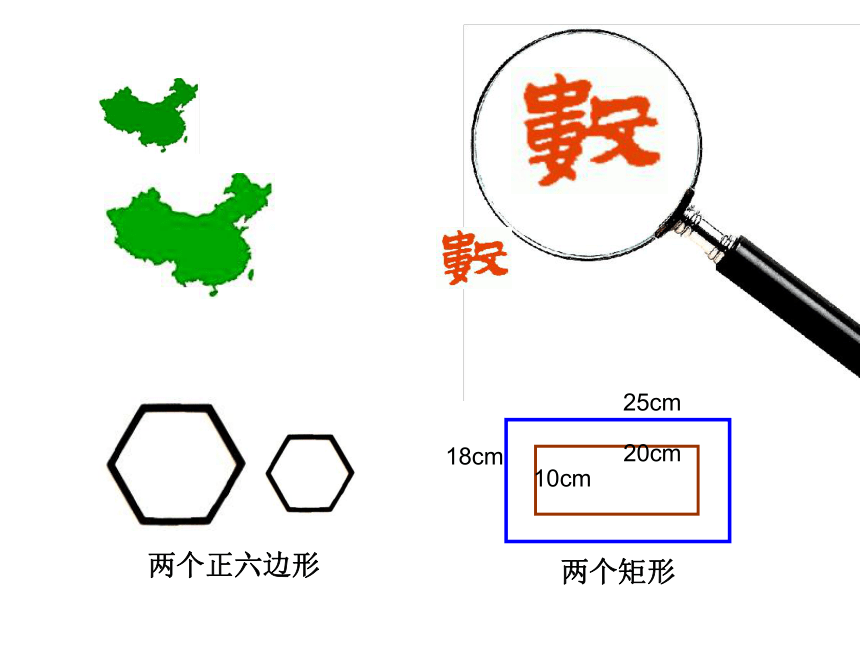
两个正六边形
两个矩形
25cm
20cm
18cm
10cm
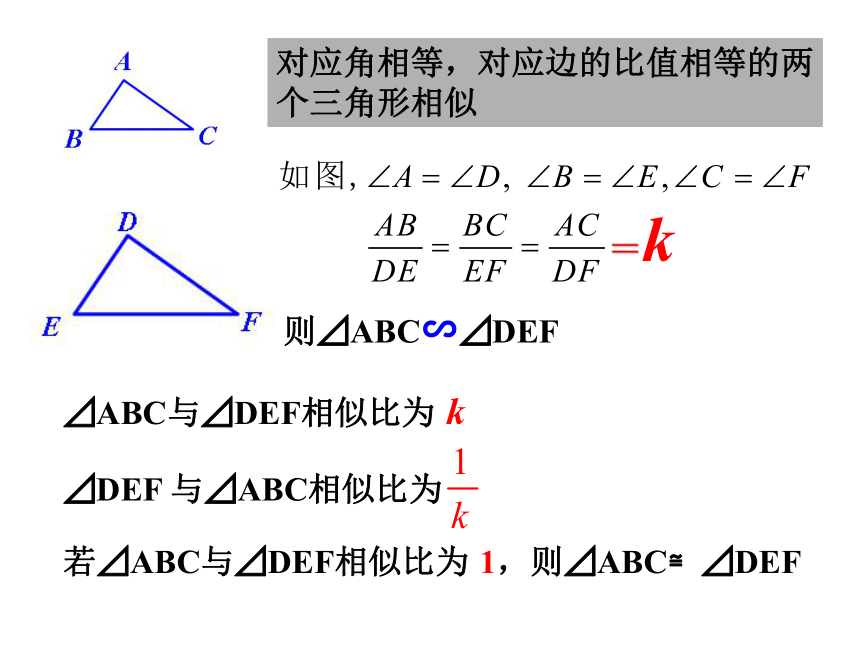
对应角相等,对应边的比值相等的两个三角形相似
则⊿ABC与⊿DEF相似
则⊿ABC∽⊿DEF
=k
⊿ABC与⊿DEF相似比为 k
⊿DEF 与⊿ABC相似比为
若⊿ABC与⊿DEF相似比为 1,则⊿ABC≌⊿DEF
人教版义务教育标准实验教材九年级(下)
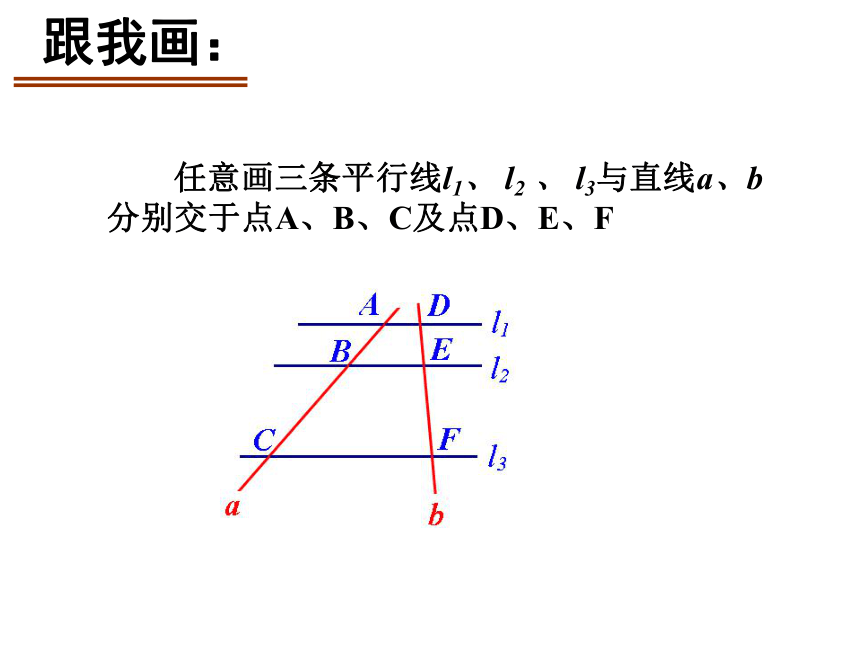
跟我画:
任意画三条平行线l1、 l2 、 l3与直线a、b分别交于点A、B、C及点D、E、F
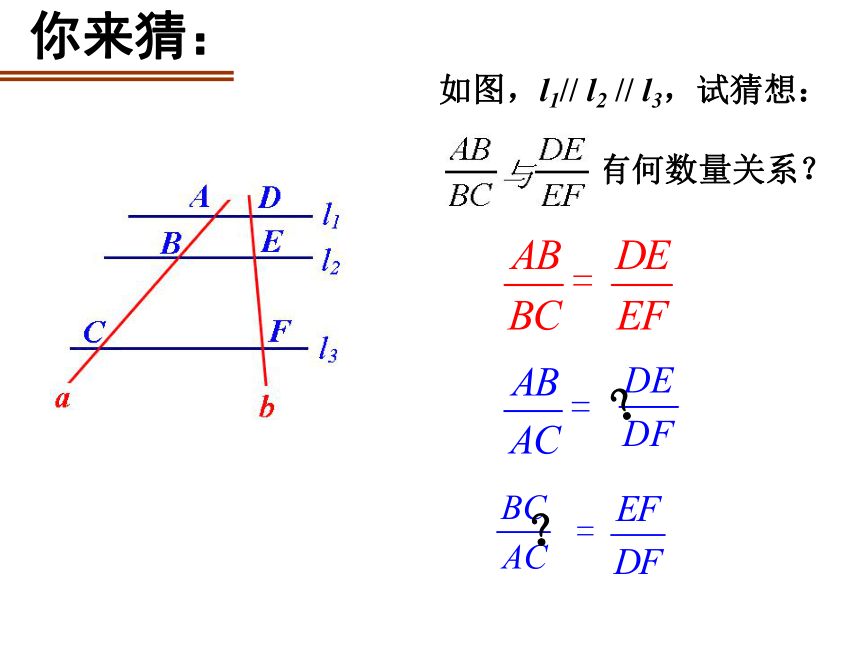
如图,l1// l2 // l3,试猜想:
有何数量关系?
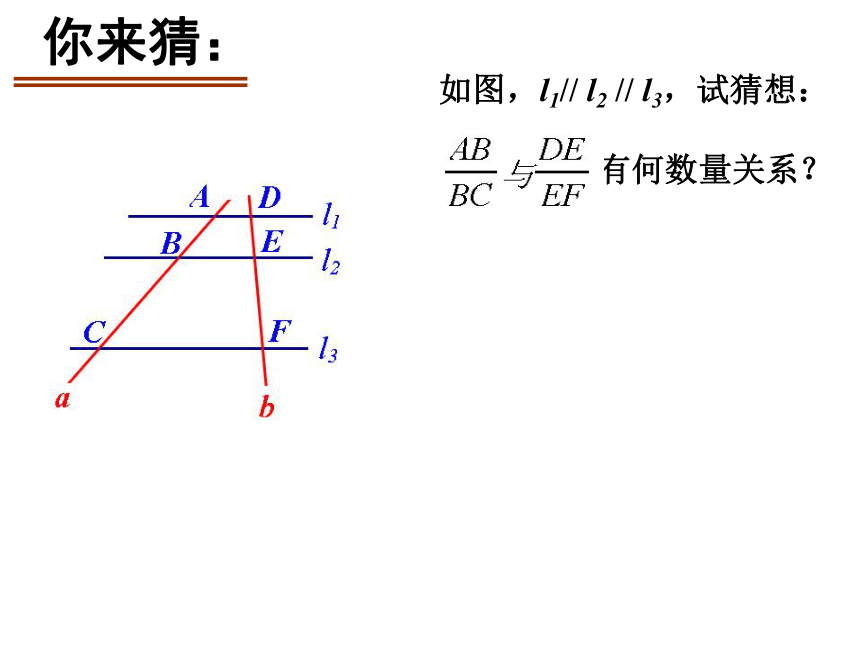
你来猜:
如图,l1// l2 // l3,试猜想:
有何数量关系?
你来猜:
?
?
三条平行线截两条直线所得的对应线段的比相等
平行线分线段成比例定理:
∵ l1// l2 // l3
∴
分析归纳:
推论:平行于三角形一边的直线截其它两边(或两边的延长线),所得的对应线段的比相等.
发展变化:
变化创新:
如图,已知AD//ME//BC,且DF//AB,则下
列与 相等的有 .
①
②
③
④
=
=
变式:如图,在⊿ABC中,ME//BC;
(1)
相等的线段比.
找出与
(2)图中的⊿AME与⊿ABC相似吗?
F
反思归纳:
∵ DE//BC
∴⊿ADE∽⊿ABC
【判定三角形相似的定理】
平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似.
“A字型”
如图,D、E、F分别在⊿ABC的三边上,DE//BC,EF//AB,且AD=2,BD=3.
(1)说出下列线段的比值
(2)图中有几对相似三角形?
并说出它们的相似比.
(3)若DE=6cm,求CF的长
展示自我:
谈谈收获,
说说疑问.
小结梳理:
一个推论:
两个定理:
三种方法:
平行线分线段成比例定理
判定三角形相似的定理
相似三角形的定义
判定三角形相似的定理
相似三角形的传递性
“A”
“X”
平行→成比例线段
平行→相似
平行→相似
?
如图,AB、CD相交于点O,AC//BD;
问:⊿AOC与⊿BOD相似吗?为什么?
思考题:
两个正六边形
两个矩形
25cm
20cm
18cm
10cm
对应角相等,对应边的比值相等的两个三角形相似
则⊿ABC与⊿DEF相似
则⊿ABC∽⊿DEF
=k
⊿ABC与⊿DEF相似比为 k
⊿DEF 与⊿ABC相似比为
若⊿ABC与⊿DEF相似比为 1,则⊿ABC≌⊿DEF
人教版义务教育标准实验教材九年级(下)
跟我画:
任意画三条平行线l1、 l2 、 l3与直线a、b分别交于点A、B、C及点D、E、F
如图,l1// l2 // l3,试猜想:
有何数量关系?
你来猜:
如图,l1// l2 // l3,试猜想:
有何数量关系?
你来猜:
?
?
三条平行线截两条直线所得的对应线段的比相等
平行线分线段成比例定理:
∵ l1// l2 // l3
∴
分析归纳:
推论:平行于三角形一边的直线截其它两边(或两边的延长线),所得的对应线段的比相等.
发展变化:
变化创新:
如图,已知AD//ME//BC,且DF//AB,则下
列与 相等的有 .
①
②
③
④
=
=
变式:如图,在⊿ABC中,ME//BC;
(1)
相等的线段比.
找出与
(2)图中的⊿AME与⊿ABC相似吗?
F
反思归纳:
∵ DE//BC
∴⊿ADE∽⊿ABC
【判定三角形相似的定理】
平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似.
“A字型”
如图,D、E、F分别在⊿ABC的三边上,DE//BC,EF//AB,且AD=2,BD=3.
(1)说出下列线段的比值
(2)图中有几对相似三角形?
并说出它们的相似比.
(3)若DE=6cm,求CF的长
展示自我:
谈谈收获,
说说疑问.
小结梳理:
一个推论:
两个定理:
三种方法:
平行线分线段成比例定理
判定三角形相似的定理
相似三角形的定义
判定三角形相似的定理
相似三角形的传递性
“A”
“X”
平行→成比例线段
平行→相似
平行→相似
?
如图,AB、CD相交于点O,AC//BD;
问:⊿AOC与⊿BOD相似吗?为什么?
思考题:
