2020-2021学年北京版小学六年级数学下册《第2章 比和比例》单元测试题(有答案)
文档属性
| 名称 | 2020-2021学年北京版小学六年级数学下册《第2章 比和比例》单元测试题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 253.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览




文档简介
2020-2021学年北京版小学六年级数学下册《第2章
比和比例》单元测试题
一.选择题(共8小题)
1.比的前项相当于分数中的( )
A.分子
B.分母
C.分数线
2.完成同一份稿件,甲用小时,乙用小时,甲、乙的工作效率比是( )
A.6:5
B.不能确定
C.5:6
D.25:36
3.一个长方体,宽是长的,宽是高的.这个长方体长、宽、高的最简整数比是( )
A.10:5:6
B.6:5:1
C.10:5:2
4.下列各比中能与12:6组成比例的是( )
A.2:4
B.0.8:0.04
C.9:3
D.6:3
5.如果x=y,那么x与y成( )比例。
A.正
B.反
C.不成
D.无法确定
6.圆的周长和直径( )
A.成正比例
B.成反比例
C.不成比例
7.x、y、z是三个非零自然数,且x×=y×=z×,那么x、y、z按照从大到小的顺序排列应是( )
A.x>y>z
B.z>y>x
C.y>x>z
D.y>z>x
8.学校操场的长是200米,把它画在比例尺是1:10000的图上,应画( )
A.2分米
B.2厘米
C.2毫米
二.填空题(共10小题)
9.=Y,XY成
比例;=Y,XY成
比例.
10.是
比例尺,把它改写成数值比例尺是
。
11.在2:5中,如果比的前项乘4,要使比值不变,后项应加上
.
12.已知,求x.
13.把改写成数值比例尺是
.
14.在一幅比例尺是的地图上,量得甲、乙两地的距离是8.2厘米,它的实际距离是
千米,如果把一个长1.2毫米的零件,在图上用24厘米表示,则这幅地图的比例尺是
.
15.在比例中,两个外项的积一定,两个两内项成
比例.
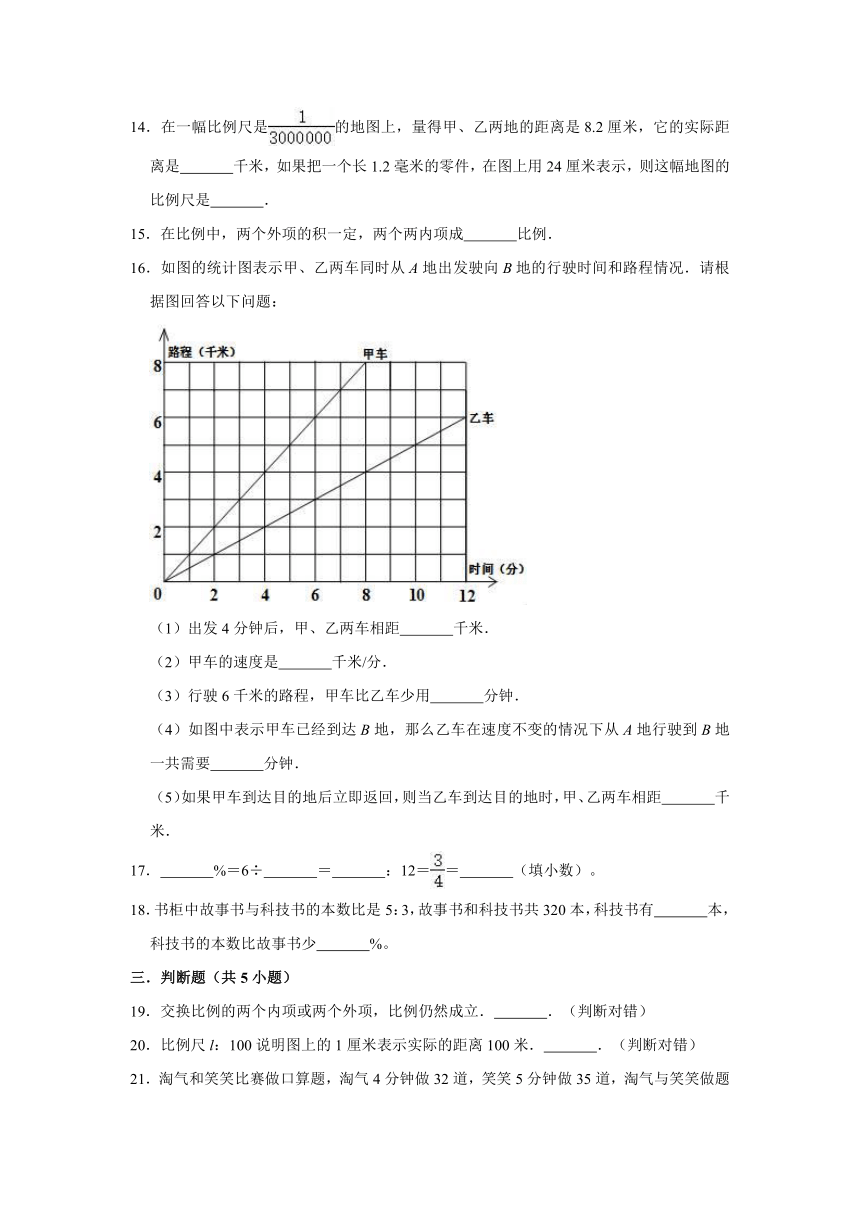
16.如图的统计图表示甲、乙两车同时从A地出发驶向B地的行驶时间和路程情况.请根据图回答以下问题:
(1)出发4分钟后,甲、乙两车相距
千米.
(2)甲车的速度是
千米/分.
(3)行驶6千米的路程,甲车比乙车少用
分钟.
(4)如图中表示甲车已经到达B地,那么乙车在速度不变的情况下从A地行驶到B地一共需要
分钟.
(5)如果甲车到达目的地后立即返回,则当乙车到达目的地时,甲、乙两车相距
千米.
17.
%=6÷
=
:12==
(填小数)。
18.书柜中故事书与科技书的本数比是5:3,故事书和科技书共320本,科技书有
本,科技书的本数比故事书少
%。
三.判断题(共5小题)
19.交换比例的两个内项或两个外项,比例仍然成立.
.(判断对错)
20.比例尺l:100说明图上的1厘米表示实际的距离100米.
.(判断对错)
21.淘气和笑笑比赛做口算题,淘气4分钟做32道,笑笑5分钟做35道,淘气与笑笑做题的速度比是32:35。
(判断对错)
22.y=(k一定),x和y成反比例.
.
23.今年小军的年龄和爸爸的年龄比是1:6,那么5年后小军和爸爸的年龄比仍然是1:6。
(判断对错)
四.计算题(共1小题)
24.求未知数x的值。
0.75:x=1.25:
=
35%x﹣x=0.5
五.操作题(共1小题)
25.如图每个方格的边长表示1厘米。画一个长方形,面积是24平方厘米,长与宽的比是3:2。再画长方形,周长是24厘米,长与宽的比是2:1。
六.应用题(共7小题)
26.广场上摆放了一些盆花,兰花和茶花数量的比是2:3.如果兰花摆放60盆,茶花需要多少盆?
27.甲、乙两个粮仓的存粮数的比是4:3,如果从甲粮仓拿出1200千克放入乙粮仓,这时甲粮仓存粮数是乙粮仓存粮数的.
①甲、乙两粮仓共有粮多少千克?
②甲粮仓原有粮多少千克?
28.六(2)班有40人参加运动会,男女运动员人数之比是5:3,女运动员中有获奖,获奖的女运动员有多少人?
29.张师傅两天加工一批零件,第一天完成的个数比零件总个数的多60个,第二天完成的个数与第一天完成的比是1:3。这批零件一共有多少个?
30.学校购买了一批新书,分给高年级后,剩下的按4:3分给中年级和低年级,已知中年级分得240本.这批新书一共有多少本?
31.某小学六(三)班女生人数与男生人数的比是5:4,女生有30人.这个班的学生数占全校学生总数的5%,这所学校共有学生多少人?
32.一把刀售价3元.如果小明买这把刀,剩下的钱与小强的钱数比是2:5,现在小强买了这把刀而小明没买,小明的钱与小强剩下钱数的比是8:13,小明原有多少钱?
参考答案与试题解析
一.选择题(共8小题)
1.解:比的前项相当于分数中的分子.
故选:A.
2.解:设这份稿件的工作总量为10,
10÷=30
10÷=25
30:25=6:5
答:甲、乙的工作效率比是6:5。
故选:A。
3.解:宽是长的,
长与宽的比是2:1,
宽是高的,宽与高的比5:6,
长与宽的比是2:1=10:5,
所以长方体长、宽、高的最简整数比是10:5:6.
故选:A.
4.解:12:6
=12÷6
=2
A.2:4
=2÷4
=
B.0.8:0.04
=0.8÷0.04
=20
C.9:3
=9÷3
=3
D.6:3
=6÷3
=2
所以12:6能与6:3组成比例。
故选:D。
5.解:如果x=y,即x:y=(一定),是比值一定,那么x与y成正比例。
故选:A。
6.解:圆的周长公式:C=πd,
可以推出:C:d=π(一定);
圆的周长和直径是两种相关联的量,圆的周长随直径的变化而变化,π一定,也就是圆的周长和对应的直径的比值一定,所以圆的周长和直径是成正比例关系.
故选:A。
7.解:由x×,利用比例的基本性质可得:
x:y=:=():()=40:42=20:21,
所以x<y,
由y×=z×,利用比例的基本性质可得:
y:z==():()=70:72=35:36,
所以y<z,
所以x<y<z.
故选:B。
8.解:200米=20000厘米,
20000×=2(厘米)
答:应画2厘米;
故选:B.
二.填空题(共12小题)
9.解:因为,=Y,则X:Y=5(一定);
所以,XY成正比例;
因为,=Y,则XY=5(一定);
所以,XY成反比例.
故答案为:正,反.
10.解:是线段比例尺。
80千米=8000000厘米
数值比例尺是1:8000000
答:是线段比例尺,把它改写成数值比例尺是1:8000000。
11.解:5×4﹣5=15
在2:5中,如果比的前项乘4,要使比值不变,后项应加上15.
故答案为:15.
12.解:1.8:x=2:3
x×2=1.8×3
x=×
x=6
x=6
x=6×
x=
故答案为:.
13.解:由题意可知:此线段比例尺表示的是图上距离1厘米代表实际距离40千米,
又因40千米=4000000厘米,
则1厘米:4000000厘米=1:4000000;
故答案为:1:4000000.
14.解:8.2÷=24600000(厘米)=246(千米);
24厘米=240毫米,
240:1.2=200:1.
故答案为:246、200:1.
15.解:内项×内项=外项×外项(一定),
可以看出,两内项是两种相关联的量,一内项随另一内项的变化而变化,
两外项的积一定,也就是两内项相对应数的乘积一定,所以两内项成反比例关系.
故答案为:反.
16.解:(1)甲车4分钟行驶4千米,乙车4分钟行驶2千米,
4﹣2=2(千米);
答:出发4分钟后,甲、乙两车相距2千米.
(2)从图中可以看出,甲车的速度是1千米/分;
(3)从图中可以看出,甲车行驶6千米,用6分钟;乙车行驶6千米,用12分钟,
12﹣6=6(分钟);
答:甲车比乙车少用6分钟.
(4)根据乙车4分钟行驶2千米,
8÷(2÷4)
=8÷0.5
=16(分钟);
答:乙车在速度不变的情况下从A地行驶到B地一共需要16分钟.
(5)8÷8=1(小时)
12÷6=2(小时)
2﹣1=1(小时)
8×1=8(千米)
答:甲、乙两车相距8千米.
故答案为:2;1;6;16;8.
17.解:75%=6÷8=9:12==0.75
故答案为:75,8,9,0.75。
18.解:320×
=320×
=120(本)
(5﹣3)÷5
=2÷5
=0.4
=40%
答:科技书有120本,科技书的本数比故事书少40%。
故答案为:120,40。
三.判断题(共5小题)
19.解:在一个比例中,两个外项交换位置后,两内项之积仍然等于两外项之积,
所以仍是比例;
例如:2:3=4:6,
6:3=4:2;
故答案为:√.
20.解:比例尺l:100说明图上的1厘米表示实际的距离100厘米.
故答案为:×
21.解:(32÷4):(35÷5)=8:7
所以原题说法错误。
故答案为:×。
22.解:因为
y=(k一定),
所以XY=2K﹣1
(一定)(K一定,2和1是常量,所以2K﹣1也一定),
可以看出,X和Y是两种相关联的量,X随Y的变化而变化,
2K﹣1是一定的,也就是X与Y相对应数的乘积一定,所以X与Y成反比例关系.
故答案为:正确.
23.解:假设小军今年5岁,爸爸今年30岁,
他们的年龄比为5:30=1:6,
5年后,小军10岁,爸爸35岁,
他们的年龄比为10:35=2:7;
原题说法错误。
故答案为:×。
四.计算题(共1小题)
24.解:(1)0.75:x=1.25:
1.25x=0.75×
1.25x÷1.25=0.75×÷1.25
x=0.2
(2)=
0.6x=2×0.15
0.6x÷0.6=2×0.15÷0.6
x=0.5
(3)35%x﹣x=0.5
0.1x=0.5
0.1x÷0.1=0.5÷0.1
x=5
五.操作题(共1小题)
25.解:24=24×1=12÷2=6×4,即长24厘米,宽1厘米或长12厘米,宽2厘米或长6厘米,宽4厘米的长方形面积都是24平方厘米,只有长6厘米,宽4厘米的长方形长与宽的比是6:4=3:2;
24÷2=12(厘米),即长方形的长、宽之和是12厘米,12=11+1=10+2+9+3+8+4=7+5,即可画长11厘米,宽1厘米或长10厘米,宽2厘米或长9厘米,宽3厘米,宽长8厘米,宽4厘米或长7厘米,宽5厘米的长方形,只有长8厘米,宽4厘米的长方形长与宽的比是8:4=2:1。
画图如下(红色部分为面积是24平方厘米的长方形,绿色部分为周长是24厘米的长方形):
六.应用题(共7小题)
26.解:60÷2×3
=30×3
=90(盆)
答:茶花需要90盆.
27.解:①1200÷(﹣)
=1200÷(﹣)
=1200÷
=7000(千克)
答:甲、乙两粮仓共有粮7000千克.
②7000×
=7000×
=4000(千克)
答:甲粮仓原有粮4000千克.
28.解:40××
=40××
=15×
=10(人)
答:获奖的女运动员有10人.
29.解:60÷(1﹣﹣)
=60÷(1﹣﹣)
=60÷
=400(个)
答:这批零件一共有400个。
30.解:240÷÷(1﹣)
=240÷÷
=420÷
=700(本)
答:这批新书一共有700本。
31.解:女生人数与男生人数的比是5:4,把女生人数看成5份,男生人数就是4份,
30÷5×4
=6×4
=24(人)
(30+24)÷5%
=54÷5%
=1080(人)
答:这所学校共有学生1080人.
32.解:设小明买下这把刀剩下的钱为2x元,则小强原有5x元,
(2x+3):(5x﹣3)=8:13
(5x﹣3)×8=(2x+3)×13
40x﹣24=26x+39
14x=63
x=4.5
4.5×2+3
=9+3
=12(元)
答:小明原有12元钱.
比和比例》单元测试题
一.选择题(共8小题)
1.比的前项相当于分数中的( )
A.分子
B.分母
C.分数线
2.完成同一份稿件,甲用小时,乙用小时,甲、乙的工作效率比是( )
A.6:5
B.不能确定
C.5:6
D.25:36
3.一个长方体,宽是长的,宽是高的.这个长方体长、宽、高的最简整数比是( )
A.10:5:6
B.6:5:1
C.10:5:2
4.下列各比中能与12:6组成比例的是( )
A.2:4
B.0.8:0.04
C.9:3
D.6:3
5.如果x=y,那么x与y成( )比例。
A.正
B.反
C.不成
D.无法确定
6.圆的周长和直径( )
A.成正比例
B.成反比例
C.不成比例
7.x、y、z是三个非零自然数,且x×=y×=z×,那么x、y、z按照从大到小的顺序排列应是( )
A.x>y>z
B.z>y>x
C.y>x>z
D.y>z>x
8.学校操场的长是200米,把它画在比例尺是1:10000的图上,应画( )
A.2分米
B.2厘米
C.2毫米
二.填空题(共10小题)
9.=Y,XY成
比例;=Y,XY成
比例.
10.是
比例尺,把它改写成数值比例尺是
。
11.在2:5中,如果比的前项乘4,要使比值不变,后项应加上
.
12.已知,求x.
13.把改写成数值比例尺是
.
14.在一幅比例尺是的地图上,量得甲、乙两地的距离是8.2厘米,它的实际距离是
千米,如果把一个长1.2毫米的零件,在图上用24厘米表示,则这幅地图的比例尺是
.
15.在比例中,两个外项的积一定,两个两内项成
比例.
16.如图的统计图表示甲、乙两车同时从A地出发驶向B地的行驶时间和路程情况.请根据图回答以下问题:
(1)出发4分钟后,甲、乙两车相距
千米.
(2)甲车的速度是
千米/分.
(3)行驶6千米的路程,甲车比乙车少用
分钟.
(4)如图中表示甲车已经到达B地,那么乙车在速度不变的情况下从A地行驶到B地一共需要
分钟.
(5)如果甲车到达目的地后立即返回,则当乙车到达目的地时,甲、乙两车相距
千米.
17.
%=6÷
=
:12==
(填小数)。
18.书柜中故事书与科技书的本数比是5:3,故事书和科技书共320本,科技书有
本,科技书的本数比故事书少
%。
三.判断题(共5小题)
19.交换比例的两个内项或两个外项,比例仍然成立.
.(判断对错)
20.比例尺l:100说明图上的1厘米表示实际的距离100米.
.(判断对错)
21.淘气和笑笑比赛做口算题,淘气4分钟做32道,笑笑5分钟做35道,淘气与笑笑做题的速度比是32:35。
(判断对错)
22.y=(k一定),x和y成反比例.
.
23.今年小军的年龄和爸爸的年龄比是1:6,那么5年后小军和爸爸的年龄比仍然是1:6。
(判断对错)
四.计算题(共1小题)
24.求未知数x的值。
0.75:x=1.25:
=
35%x﹣x=0.5
五.操作题(共1小题)
25.如图每个方格的边长表示1厘米。画一个长方形,面积是24平方厘米,长与宽的比是3:2。再画长方形,周长是24厘米,长与宽的比是2:1。
六.应用题(共7小题)
26.广场上摆放了一些盆花,兰花和茶花数量的比是2:3.如果兰花摆放60盆,茶花需要多少盆?
27.甲、乙两个粮仓的存粮数的比是4:3,如果从甲粮仓拿出1200千克放入乙粮仓,这时甲粮仓存粮数是乙粮仓存粮数的.
①甲、乙两粮仓共有粮多少千克?
②甲粮仓原有粮多少千克?
28.六(2)班有40人参加运动会,男女运动员人数之比是5:3,女运动员中有获奖,获奖的女运动员有多少人?
29.张师傅两天加工一批零件,第一天完成的个数比零件总个数的多60个,第二天完成的个数与第一天完成的比是1:3。这批零件一共有多少个?
30.学校购买了一批新书,分给高年级后,剩下的按4:3分给中年级和低年级,已知中年级分得240本.这批新书一共有多少本?
31.某小学六(三)班女生人数与男生人数的比是5:4,女生有30人.这个班的学生数占全校学生总数的5%,这所学校共有学生多少人?
32.一把刀售价3元.如果小明买这把刀,剩下的钱与小强的钱数比是2:5,现在小强买了这把刀而小明没买,小明的钱与小强剩下钱数的比是8:13,小明原有多少钱?
参考答案与试题解析
一.选择题(共8小题)
1.解:比的前项相当于分数中的分子.
故选:A.
2.解:设这份稿件的工作总量为10,
10÷=30
10÷=25
30:25=6:5
答:甲、乙的工作效率比是6:5。
故选:A。
3.解:宽是长的,
长与宽的比是2:1,
宽是高的,宽与高的比5:6,
长与宽的比是2:1=10:5,
所以长方体长、宽、高的最简整数比是10:5:6.
故选:A.
4.解:12:6
=12÷6
=2
A.2:4
=2÷4
=
B.0.8:0.04
=0.8÷0.04
=20
C.9:3
=9÷3
=3
D.6:3
=6÷3
=2
所以12:6能与6:3组成比例。
故选:D。
5.解:如果x=y,即x:y=(一定),是比值一定,那么x与y成正比例。
故选:A。
6.解:圆的周长公式:C=πd,
可以推出:C:d=π(一定);
圆的周长和直径是两种相关联的量,圆的周长随直径的变化而变化,π一定,也就是圆的周长和对应的直径的比值一定,所以圆的周长和直径是成正比例关系.
故选:A。
7.解:由x×,利用比例的基本性质可得:
x:y=:=():()=40:42=20:21,
所以x<y,
由y×=z×,利用比例的基本性质可得:
y:z==():()=70:72=35:36,
所以y<z,
所以x<y<z.
故选:B。
8.解:200米=20000厘米,
20000×=2(厘米)
答:应画2厘米;
故选:B.
二.填空题(共12小题)
9.解:因为,=Y,则X:Y=5(一定);
所以,XY成正比例;
因为,=Y,则XY=5(一定);
所以,XY成反比例.
故答案为:正,反.
10.解:是线段比例尺。
80千米=8000000厘米
数值比例尺是1:8000000
答:是线段比例尺,把它改写成数值比例尺是1:8000000。
11.解:5×4﹣5=15
在2:5中,如果比的前项乘4,要使比值不变,后项应加上15.
故答案为:15.
12.解:1.8:x=2:3
x×2=1.8×3
x=×
x=6
x=6
x=6×
x=
故答案为:.
13.解:由题意可知:此线段比例尺表示的是图上距离1厘米代表实际距离40千米,
又因40千米=4000000厘米,
则1厘米:4000000厘米=1:4000000;
故答案为:1:4000000.
14.解:8.2÷=24600000(厘米)=246(千米);
24厘米=240毫米,
240:1.2=200:1.
故答案为:246、200:1.
15.解:内项×内项=外项×外项(一定),
可以看出,两内项是两种相关联的量,一内项随另一内项的变化而变化,
两外项的积一定,也就是两内项相对应数的乘积一定,所以两内项成反比例关系.
故答案为:反.
16.解:(1)甲车4分钟行驶4千米,乙车4分钟行驶2千米,
4﹣2=2(千米);
答:出发4分钟后,甲、乙两车相距2千米.
(2)从图中可以看出,甲车的速度是1千米/分;
(3)从图中可以看出,甲车行驶6千米,用6分钟;乙车行驶6千米,用12分钟,
12﹣6=6(分钟);
答:甲车比乙车少用6分钟.
(4)根据乙车4分钟行驶2千米,
8÷(2÷4)
=8÷0.5
=16(分钟);
答:乙车在速度不变的情况下从A地行驶到B地一共需要16分钟.
(5)8÷8=1(小时)
12÷6=2(小时)
2﹣1=1(小时)
8×1=8(千米)
答:甲、乙两车相距8千米.
故答案为:2;1;6;16;8.
17.解:75%=6÷8=9:12==0.75
故答案为:75,8,9,0.75。
18.解:320×
=320×
=120(本)
(5﹣3)÷5
=2÷5
=0.4
=40%
答:科技书有120本,科技书的本数比故事书少40%。
故答案为:120,40。
三.判断题(共5小题)
19.解:在一个比例中,两个外项交换位置后,两内项之积仍然等于两外项之积,
所以仍是比例;
例如:2:3=4:6,
6:3=4:2;
故答案为:√.
20.解:比例尺l:100说明图上的1厘米表示实际的距离100厘米.
故答案为:×
21.解:(32÷4):(35÷5)=8:7
所以原题说法错误。
故答案为:×。
22.解:因为
y=(k一定),
所以XY=2K﹣1
(一定)(K一定,2和1是常量,所以2K﹣1也一定),
可以看出,X和Y是两种相关联的量,X随Y的变化而变化,
2K﹣1是一定的,也就是X与Y相对应数的乘积一定,所以X与Y成反比例关系.
故答案为:正确.
23.解:假设小军今年5岁,爸爸今年30岁,
他们的年龄比为5:30=1:6,
5年后,小军10岁,爸爸35岁,
他们的年龄比为10:35=2:7;
原题说法错误。
故答案为:×。
四.计算题(共1小题)
24.解:(1)0.75:x=1.25:
1.25x=0.75×
1.25x÷1.25=0.75×÷1.25
x=0.2
(2)=
0.6x=2×0.15
0.6x÷0.6=2×0.15÷0.6
x=0.5
(3)35%x﹣x=0.5
0.1x=0.5
0.1x÷0.1=0.5÷0.1
x=5
五.操作题(共1小题)
25.解:24=24×1=12÷2=6×4,即长24厘米,宽1厘米或长12厘米,宽2厘米或长6厘米,宽4厘米的长方形面积都是24平方厘米,只有长6厘米,宽4厘米的长方形长与宽的比是6:4=3:2;
24÷2=12(厘米),即长方形的长、宽之和是12厘米,12=11+1=10+2+9+3+8+4=7+5,即可画长11厘米,宽1厘米或长10厘米,宽2厘米或长9厘米,宽3厘米,宽长8厘米,宽4厘米或长7厘米,宽5厘米的长方形,只有长8厘米,宽4厘米的长方形长与宽的比是8:4=2:1。
画图如下(红色部分为面积是24平方厘米的长方形,绿色部分为周长是24厘米的长方形):
六.应用题(共7小题)
26.解:60÷2×3
=30×3
=90(盆)
答:茶花需要90盆.
27.解:①1200÷(﹣)
=1200÷(﹣)
=1200÷
=7000(千克)
答:甲、乙两粮仓共有粮7000千克.
②7000×
=7000×
=4000(千克)
答:甲粮仓原有粮4000千克.
28.解:40××
=40××
=15×
=10(人)
答:获奖的女运动员有10人.
29.解:60÷(1﹣﹣)
=60÷(1﹣﹣)
=60÷
=400(个)
答:这批零件一共有400个。
30.解:240÷÷(1﹣)
=240÷÷
=420÷
=700(本)
答:这批新书一共有700本。
31.解:女生人数与男生人数的比是5:4,把女生人数看成5份,男生人数就是4份,
30÷5×4
=6×4
=24(人)
(30+24)÷5%
=54÷5%
=1080(人)
答:这所学校共有学生1080人.
32.解:设小明买下这把刀剩下的钱为2x元,则小强原有5x元,
(2x+3):(5x﹣3)=8:13
(5x﹣3)×8=(2x+3)×13
40x﹣24=26x+39
14x=63
x=4.5
4.5×2+3
=9+3
=12(元)
答:小明原有12元钱.
