8.3.2(1)圆柱、圆锥、圆台、球的表面积和体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册复习巩固训练
文档属性
| 名称 | 8.3.2(1)圆柱、圆锥、圆台、球的表面积和体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册复习巩固训练 |  | |
| 格式 | doc | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 15:08:09 | ||
图片预览


文档简介
8.3.2(1)圆柱、圆锥、圆台、球的表面积和体积
一、知识梳理
1. 圆柱、圆锥、圆台的表面积
⑴ ,圆柱的侧面展开图为________.
⑵,圆锥的侧面展开图为________.
⑶,圆台的侧面展开图为________.
2. 圆柱、圆锥、圆台的体积
⑴。
⑵。
⑶。
二、重要题型
知识点一: 圆柱、圆锥、圆台的表面积
1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
A.4π B.3π C.2π D.π
2.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )
A.7 B.6 C.5 D.3
3.若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的表面积是________.
4.表面积为3π的圆锥,它的侧面展开图是一个半圆面,则该圆锥的底面直径为________.
知识点二 : 圆柱、圆锥、圆台的体积
5.已知圆锥的母线长是8,底面周长为6π,则它的体积是( )
A.9π B.9
C.3π D.3
6.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( )
A.π B.2π C.4π D.8π
7.已知某圆台的上、下底面面积分别是π,4π,侧面积是6π,则这个圆台的体积是________.
知识点三:侧面展开图的应用
8.已知某圆柱的底面周长为12,高为2,矩形ABCD是该圆柱的轴截面,则在此圆柱侧面上,从A到C的路径中,最短路径的长度为( )
A.2 B.2
C.3 D.2
9.如图所示,已知圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A.求:
(1)绳子的最短长度的平方f(x);
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
三、巩固练习
1.用边长分别为2与4的矩形作圆柱的侧面,则这个圆柱的体积为( )
A. B. C.或 D.或
2.在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B. C. D.2π
3.圆台的上、下底面半径分别是10 cm和20 cm,它的侧面展开图扇环的圆心角是180°(如图),那么圆台的体积是________.
4.圆台的上、下底面半径和高的比为1∶4∶4,若母线长为10,则圆台的表面积为________.
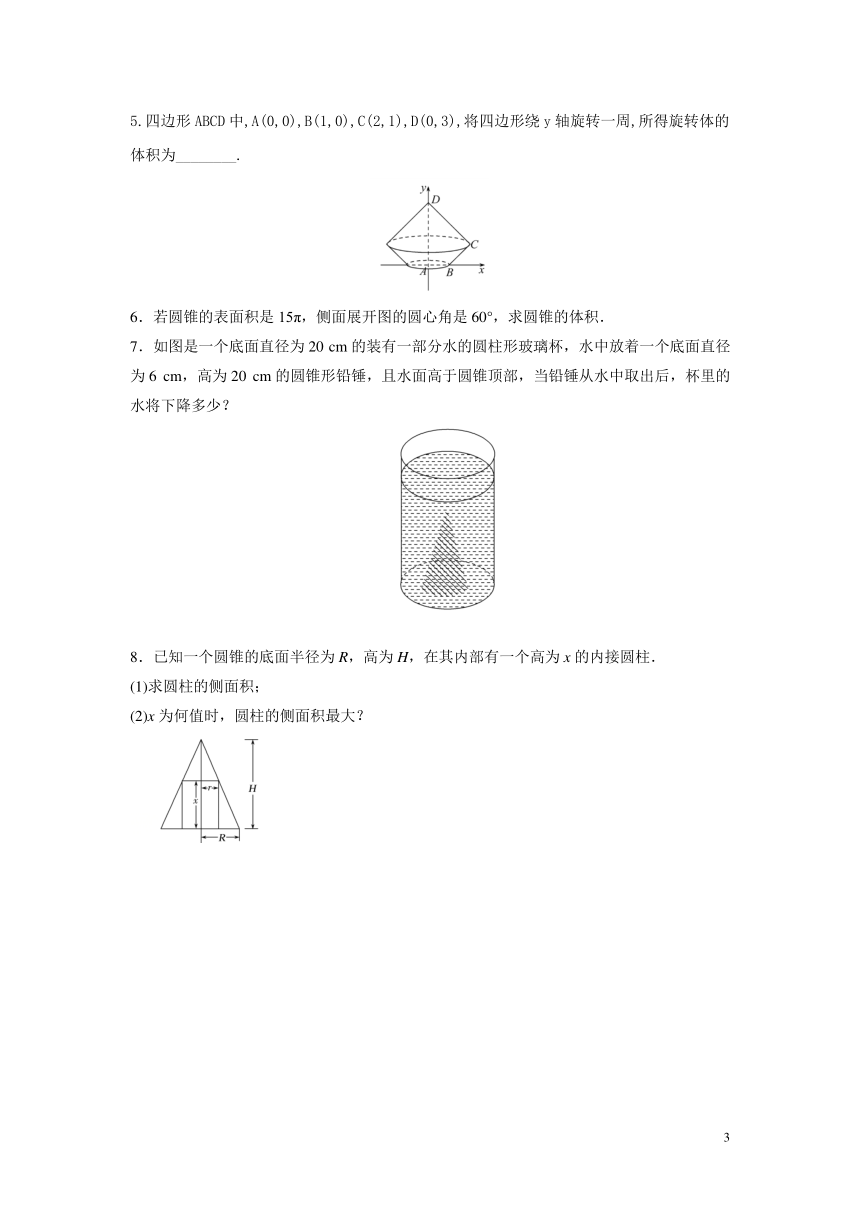
5.四边形ABCD中,A(0,0),B(1,0),C(2,1),D(0,3),将四边形绕y轴旋转一周,所得旋转体的体积为________.?
6.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积.
7.如图是一个底面直径为20 cm的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6 cm,高为20 cm的圆锥形铅锤,且水面高于圆锥顶部,当铅锤从水中取出后,杯里的水将下降多少?
8.已知一个圆锥的底面半径为R,高为H,在其内部有一个高为x的内接圆柱.
(1)求圆柱的侧面积;
(2)x为何值时,圆柱的侧面积最大?
8.3.2圆柱、圆锥、圆台、球的表面积和体积 答案
一、知识梳理
1. ⑴,矩形。⑵。⑶,扇环。
2. ⑴。⑵,。⑶,。
二、重要题型
1.C 底面圆半径为1,高为1,侧面积S=2πrh=2π×1×1=2π.故选C.
2.A 设圆台较小底面的半径为r,则另一底面的半径为3r.由S侧=π(r+3r)·3=84π,解得r=7.
3.3π 设圆锥的底面半径为r,由于轴截面面积为,则r=1,母线长为2.
∴S侧=×2×2π=2π,S底=π×12=π,∴S表=2π+π=3π.
4.2 设圆锥的母线为l,圆锥底面半径为r,由题意可知,πrl+πr2=3π,且πl=2πr,解得r=1,即直径为2.
5.C 设圆锥底面圆的半径为r,则2πr=6π,∴r=3.设圆锥的高为h,
则h==,∴V圆锥=πr2h=3π.
6.B 设圆柱的底面半径为r,则圆柱的母线长为2r,由题意得S圆柱侧=2πr×2r=4πr2=4π,所以r=1,所以V圆柱=πr2×2r=2πr3=2π.故选B.
7. 设圆台的上、下底面半径分别为r和R,母线长为l,高为h,则上底面的面积为πr2=π,所以r=1,下底面的面积为πR2=4π,所以R=2,所以侧面积为
π(R+r)l=6π,所以l=2,h=,所以V=π(12+22+1×2)×=.
8.A 圆柱的侧面展开图如图,圆柱的侧面展开图是矩形,且矩形的长为12,宽为2,则在此圆柱侧面上从A到C的最短路径为线段AC,AC==2.故选A.
9.解:将圆锥的侧面沿SA展开在平面上,如图所示,则该图为扇形,且弧AA′的长度L就是圆O的周长,∴L=2πr=2π.∴∠ASM=360°·=×360°=90°.
(1)由题意知绳子长度的最小值为展开图中的AM,其值为AM=(0≤x≤4).
f(x)=AM2=x2+16(0≤x≤4).
(2)绳子最短时,在展开图中作SR⊥AM,垂足为R,则SR的长度为顶点S到绳子的最短距离.在△SAM中,∵S△SAM=SA·SM=AM·SR,∴SR==(0≤x≤4),即绳子最短时,顶点到绳子的最短距离为(0≤x≤4).
(3)∵f(x)=x2+16(0≤x≤4)是增函数,∴f(x)的最大值为f(4)=32.
三、巩固练习
1.D 圆柱的侧面展开图是边长为2与4的矩形,当母线为2时,圆柱的底面半径是=,此时圆柱体积是π×2×2=;当母线为4时,圆柱的底面半径是=,此时圆柱的体积是π×2×4=.综上,所求圆柱的体积是或.故选D.
2.C 如图所示,过点D作BC的垂线,垂足为H.则由旋转体的定义可知,该梯形绕AD所在的直线旋转一周而形成的曲面所围成的几何体为一个圆柱挖去一个圆锥.其中圆柱的底面半径R=AB=1,高h1=BC=2,其体积V1=πR2h1=π×12×2=2π;圆锥的底面半径r=DH=1,高h2=HC=1,其体积V2=πr2h2=π×12×1=.故所求几何体的体积为V=V1-V2=2π-=.
3. cm3 180°=×360°,∴l=20,h=10,
V=π(r+r+r1r2)·h= (cm3).
4.168π 先画轴截面,再利用上、下底面半径和高的比求解.圆台的轴截面如图所示,设上底面半径为r,下底面半径为R,则它的母线长为l===5r=10,所以r=2,R=8.故S侧=π(R+r)l=π(8+2)×10=100π,S表=S侧+πr2+πR2=100π+4π+64π=168π.
5. 5π 因为C(2,1),D(0,3),所以圆锥的底面半径r=2,高h=2.
所以V圆锥=πr2h=π×22×2=π.因为B(1,0),C(2,1),
所以圆台的两个底面半径R=2,R′=1,高h′=1.
所以V圆台=πh′(R2+R′2+RR′)=π×1×(22+12+2×1)=π,所以V=V圆锥+V圆台=5π.
6.解:设圆锥的底面半径为r,母线为l,则2πr=πl,得l=6r.
又S锥=πr2+πr·6r=7πr2=15π,得r=,圆锥的高h=×,
V=πr2h=π×××=π.
7.解:因为圆锥形铅锤的体积为×π××20=60π(cm3),设水面下降的高度为x cm,则小圆柱的体积为πx=100πx.所以有60π=100πx,解此方程得x=0.6.
故杯里的水将下降0.6 cm.
8.解:(1)作圆锥的轴截面,如图所示.设圆柱底面半径为r,
因为=,所以r=R-x.所以S圆柱侧=2πrx=2πRx-x2(0(2)因为-<0,所以当x==时,S圆柱侧最大.故当x=时,即圆柱的高为圆锥高的一半时,圆柱的侧面积最大.
1
一、知识梳理
1. 圆柱、圆锥、圆台的表面积
⑴ ,圆柱的侧面展开图为________.
⑵,圆锥的侧面展开图为________.
⑶,圆台的侧面展开图为________.
2. 圆柱、圆锥、圆台的体积
⑴。
⑵。
⑶。
二、重要题型
知识点一: 圆柱、圆锥、圆台的表面积
1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
A.4π B.3π C.2π D.π
2.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )
A.7 B.6 C.5 D.3
3.若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的表面积是________.
4.表面积为3π的圆锥,它的侧面展开图是一个半圆面,则该圆锥的底面直径为________.
知识点二 : 圆柱、圆锥、圆台的体积
5.已知圆锥的母线长是8,底面周长为6π,则它的体积是( )
A.9π B.9
C.3π D.3
6.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( )
A.π B.2π C.4π D.8π
7.已知某圆台的上、下底面面积分别是π,4π,侧面积是6π,则这个圆台的体积是________.
知识点三:侧面展开图的应用
8.已知某圆柱的底面周长为12,高为2,矩形ABCD是该圆柱的轴截面,则在此圆柱侧面上,从A到C的路径中,最短路径的长度为( )
A.2 B.2
C.3 D.2
9.如图所示,已知圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A.求:
(1)绳子的最短长度的平方f(x);
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
三、巩固练习
1.用边长分别为2与4的矩形作圆柱的侧面,则这个圆柱的体积为( )
A. B. C.或 D.或
2.在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B. C. D.2π
3.圆台的上、下底面半径分别是10 cm和20 cm,它的侧面展开图扇环的圆心角是180°(如图),那么圆台的体积是________.
4.圆台的上、下底面半径和高的比为1∶4∶4,若母线长为10,则圆台的表面积为________.
5.四边形ABCD中,A(0,0),B(1,0),C(2,1),D(0,3),将四边形绕y轴旋转一周,所得旋转体的体积为________.?
6.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积.
7.如图是一个底面直径为20 cm的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6 cm,高为20 cm的圆锥形铅锤,且水面高于圆锥顶部,当铅锤从水中取出后,杯里的水将下降多少?
8.已知一个圆锥的底面半径为R,高为H,在其内部有一个高为x的内接圆柱.
(1)求圆柱的侧面积;
(2)x为何值时,圆柱的侧面积最大?
8.3.2圆柱、圆锥、圆台、球的表面积和体积 答案
一、知识梳理
1. ⑴,矩形。⑵。⑶,扇环。
2. ⑴。⑵,。⑶,。
二、重要题型
1.C 底面圆半径为1,高为1,侧面积S=2πrh=2π×1×1=2π.故选C.
2.A 设圆台较小底面的半径为r,则另一底面的半径为3r.由S侧=π(r+3r)·3=84π,解得r=7.
3.3π 设圆锥的底面半径为r,由于轴截面面积为,则r=1,母线长为2.
∴S侧=×2×2π=2π,S底=π×12=π,∴S表=2π+π=3π.
4.2 设圆锥的母线为l,圆锥底面半径为r,由题意可知,πrl+πr2=3π,且πl=2πr,解得r=1,即直径为2.
5.C 设圆锥底面圆的半径为r,则2πr=6π,∴r=3.设圆锥的高为h,
则h==,∴V圆锥=πr2h=3π.
6.B 设圆柱的底面半径为r,则圆柱的母线长为2r,由题意得S圆柱侧=2πr×2r=4πr2=4π,所以r=1,所以V圆柱=πr2×2r=2πr3=2π.故选B.
7. 设圆台的上、下底面半径分别为r和R,母线长为l,高为h,则上底面的面积为πr2=π,所以r=1,下底面的面积为πR2=4π,所以R=2,所以侧面积为
π(R+r)l=6π,所以l=2,h=,所以V=π(12+22+1×2)×=.
8.A 圆柱的侧面展开图如图,圆柱的侧面展开图是矩形,且矩形的长为12,宽为2,则在此圆柱侧面上从A到C的最短路径为线段AC,AC==2.故选A.
9.解:将圆锥的侧面沿SA展开在平面上,如图所示,则该图为扇形,且弧AA′的长度L就是圆O的周长,∴L=2πr=2π.∴∠ASM=360°·=×360°=90°.
(1)由题意知绳子长度的最小值为展开图中的AM,其值为AM=(0≤x≤4).
f(x)=AM2=x2+16(0≤x≤4).
(2)绳子最短时,在展开图中作SR⊥AM,垂足为R,则SR的长度为顶点S到绳子的最短距离.在△SAM中,∵S△SAM=SA·SM=AM·SR,∴SR==(0≤x≤4),即绳子最短时,顶点到绳子的最短距离为(0≤x≤4).
(3)∵f(x)=x2+16(0≤x≤4)是增函数,∴f(x)的最大值为f(4)=32.
三、巩固练习
1.D 圆柱的侧面展开图是边长为2与4的矩形,当母线为2时,圆柱的底面半径是=,此时圆柱体积是π×2×2=;当母线为4时,圆柱的底面半径是=,此时圆柱的体积是π×2×4=.综上,所求圆柱的体积是或.故选D.
2.C 如图所示,过点D作BC的垂线,垂足为H.则由旋转体的定义可知,该梯形绕AD所在的直线旋转一周而形成的曲面所围成的几何体为一个圆柱挖去一个圆锥.其中圆柱的底面半径R=AB=1,高h1=BC=2,其体积V1=πR2h1=π×12×2=2π;圆锥的底面半径r=DH=1,高h2=HC=1,其体积V2=πr2h2=π×12×1=.故所求几何体的体积为V=V1-V2=2π-=.
3. cm3 180°=×360°,∴l=20,h=10,
V=π(r+r+r1r2)·h= (cm3).
4.168π 先画轴截面,再利用上、下底面半径和高的比求解.圆台的轴截面如图所示,设上底面半径为r,下底面半径为R,则它的母线长为l===5r=10,所以r=2,R=8.故S侧=π(R+r)l=π(8+2)×10=100π,S表=S侧+πr2+πR2=100π+4π+64π=168π.
5. 5π 因为C(2,1),D(0,3),所以圆锥的底面半径r=2,高h=2.
所以V圆锥=πr2h=π×22×2=π.因为B(1,0),C(2,1),
所以圆台的两个底面半径R=2,R′=1,高h′=1.
所以V圆台=πh′(R2+R′2+RR′)=π×1×(22+12+2×1)=π,所以V=V圆锥+V圆台=5π.
6.解:设圆锥的底面半径为r,母线为l,则2πr=πl,得l=6r.
又S锥=πr2+πr·6r=7πr2=15π,得r=,圆锥的高h=×,
V=πr2h=π×××=π.
7.解:因为圆锥形铅锤的体积为×π××20=60π(cm3),设水面下降的高度为x cm,则小圆柱的体积为πx=100πx.所以有60π=100πx,解此方程得x=0.6.
故杯里的水将下降0.6 cm.
8.解:(1)作圆锥的轴截面,如图所示.设圆柱底面半径为r,
因为=,所以r=R-x.所以S圆柱侧=2πrx=2πRx-x2(0
1
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
