人教版八年级下册数学第十六章分式16.1.1《从分数到分式》
文档属性
| 名称 | 人教版八年级下册数学第十六章分式16.1.1《从分数到分式》 |

|
|
| 格式 | zip | ||
| 文件大小 | 475.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-18 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
(共18课时)
16.1 分式 4课时
16.2 分式的运算 7课时
16.3 分式方程 5课时
小结与复习 2课时
(教师用书安排14课时)
(一)课时安排
(二)课标要求
1.抽象出分式概念;
2.类比分数的基本性质,了解分式的基本性质;掌握分式的约分和通分法则
3.类比分数的四则运算法则,探究分式的四则运算,掌握这些运算法则;
4.结合分式的运算,将指数的讨论范围从正整数扩大到全体整数,构建和发展相联系的知识体系;
5.结合分析和解决实际问题,讨论可化为一元一次方程的分式方程,掌握这种方程的解法,体会解方程中的化归思想;利用分式方程解决实际问题,体会建模思想.
(三)教材简析
分数的类比--------分式学习的引路人
整式相关知识------分式学习必备基础
分式是分数、整式相关知识的应用与延伸
第一节 分式是整章的理论基础部分;
第二节 分式的运算是第一节理论的实践阶段, 是整章的核心;
第三节 分式方程是对分式的发展,其解法及应用充分体现了“化归”与“建模”两类重要思想.
让学生充分动起来
观察、类比、猜想、尝试(思维活动)
发现法则、理解法则、应用法则
发展学生的合情推理能力
对算理的理解、代数表达、运算能力的培养
运算复杂、出错机会增多
控制好题目的难度,不要盲目加大运算量
(四)教学建议
第1课时 §16.1.1 从分数到分式
第2课时 §16.1.2 分式的基本性质
第3课时 §16.1.2 分式的约分
第4课时 §16.1.2 分式的通分
第5课时 §16.2.1 分式的乘除
第6课时 §16.2.1 分式的乘方
第7课时 §16.2.2 分式的加减
第8课时 §16.2.2 分式的混合运算
第9课时 §16.2.2 分式的应用
第10课时 §16.2.3 负整数指数幂
第11课时 §16.2.3 科学记数法
第12课时 §16.3 分式方程
第13课时 §16.3 分式方程(2)
第14课时 §16.3 分式方程的应用(1)
第15课时 §16.3 分式方程的应用(2)
第16课时 §16.3 分式方程的应用(3)
第17课时 《分式》小结与复习(1)
第18课时 《分式》小结与复习(2)
第十六章 分式课时计划
第1课时
教学目标
1.了解分式的概念;
2.理解并能熟练分式有意义的条件,分式的值为零的条件.
重点:分式的概念,
分式有意义、分式的值为零的条件.
难点:熟练求出分式有意义、分式的值为零的条件.
利用分式与分数有许多类似之处,从分数入手,研究出分式的有关概念,同时还要讲清分式与分数的联系与区别.
突破难点的方法:
教学重点、难点
第1课时 16.1.1 从分数到分式
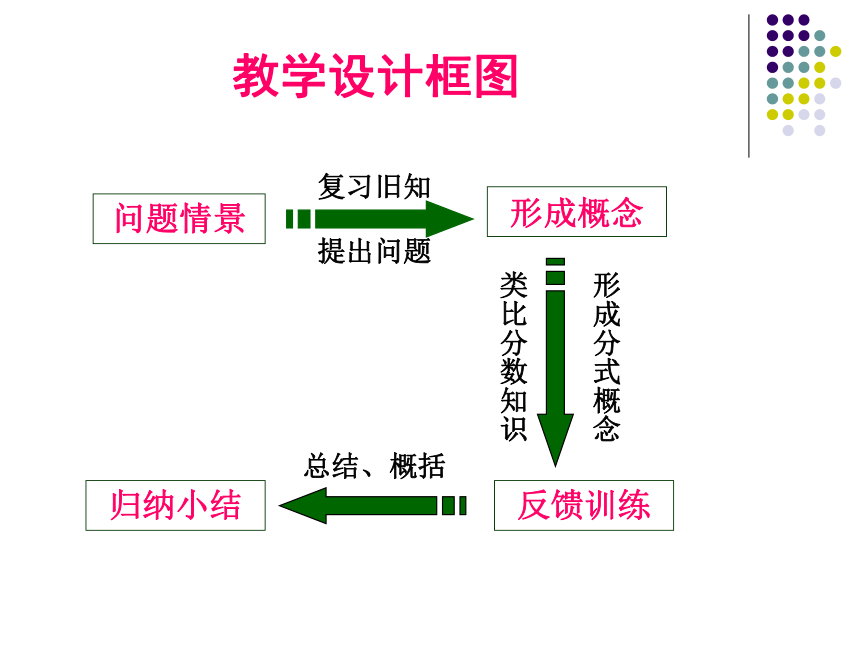
问题情景
形成概念
反馈训练
归纳小结
教学设计框图
复习旧知
类比分数知识
形成分式概念
总结、概括
提出问题
(一)问题情景(复习+问题)
(二)形成概念(类比+归纳)
(三)例题设计(原1+补3)
(四)配套练习(课本P4+补充)
(五)归纳小结(3点+2个)
(六)课后作业(课本P8-2,3,8,13)
教学过程六环节
我们学过的代数式中有单项式、多项式、整式,请你判定下列说法是否正确
(1)2x是单项式,也是整式 ( )
(2) 和0都是单项式,也都是整式 ( )
(3)2x-1是多项式,也是整式 ( )
(4) 是多项式,也是整式 ( )
单项式、多项式统称整式
(一)问题情景
整式
多项式
单项式、多项式统称整式
单项式
(5) 是单项式,也是整式 ( )
(6) 是多项式,也是整式 ( )
既不是单项式又不是多项式,即不是整式的另一类式子----新旧知识的碰撞
1.长方形的面积为10cm ,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______;
S
a
实际问题(课本P2)
2.把体积为200cm 的水倒入底面积为
33cm 的圆柱形容器中,水面高度为
_____cm;把体积为V的水倒入底面积为S
的圆柱形容器中,水面高度为______;
V
S
观察式子 和 , 和 ,辨析它们的相同点和不同点.
都具有分数的形式
相同点
不同点
(观察分母)
分母中有无字母
辨析、思考
两个整式相除的商,分数线可以理解为除号
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式。其中A叫做分式的分子,B为分式的分母。
注意:分式是不同于整式的另一类有理式,且分母中含有字母是分式的一大特点。
(二)形成概念
整式
多项式
单项式
分式
有理式
例1(补充)下面的式子哪些是分式?
(三)例题设计
探究(1)(补充)
思考1 根据下列 的值填表.
……
……
……
……
……
……
0
1
问题: 分式 在什么条件下有意义?
结论:(1)分式中B≠0时,分式 有意义;
(2)分式中B=0,分式 无意义.
该怎样做?
变式练习 若把题目要求改为:“当 取何值时下列分式无意义?”
例2 (补充)当x取什么值时,下列分式有意义?
; (2) ;
(3) ; (4) .
(三)例题设计
思考2 分式 在什么条件下值为0?
归纳 分式的值要为0,需满足的条件是:分子的值等于0且分母值不为0.
仅仅是 就可以了吗?
例3(补充)当 是什么值时,分式的 值是0?
探究(2)
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
例4(补充).已知分式 ,
(3) 当x为何值时,分式的值为零
三种形式
的值为负;
的值为正.
当x 时,
例5(补充)当x 时,
探究(3)附加问题
思考3 分式 在什么条件下值为正?
分式 在什么条件下值为负?
归纳 (1)当A、B同号时,分式 的值为正;
(2)当A、B同号时,分式 的值为负.
1.列式表示下列各量:
(1)某村有n个人,耕地40公顷,人均耕地
面积为_____________公顷;
(2)△ABC的面积为S,BC边长为a,
高AD为_____________;
(3)一辆汽车行驶 千米用 小时,它的平均
速度为____千米/时;一列火车行驶 千米比
这辆汽车少用t小时,它的平均车速为____千米/时.
课本P4 练习 1-3
(四)配套练习(课本P4+例1+补充)
(课本P3例1-当作练习)
练习:下列各式中,无论x取何值,分式都有意义的是( )
C.
A.
B.
D.
(补充)
★ 学习内容:分式的概念 数学思想:类比
1.分式 有意义的条件是__________.
3.分式 值为0的条件是_____________.
2.分式 无意义的条件是__________.
4.分式 值为正的条件是_____________.
5.分式 值为负的条件是_____________.
(五)归纳小结(3个+2点)
分式有意义的条件:
分式的分母不等于零
分式的值为零的条件:
分式的分子等于零
且分母不等于零
分式无意义的条件:
分式的分母等于零
分式的值为正或负的条件:
同号得正,异号得负
(六)课后作业
课本P8-1(直接写在课本) 课本P8-2,3,13
(一)创设情景(复习+问题)
(二)形成概念(类比+归纳)
(三)例题设计(原1+补3)
(四)配套练习(课本P4+补充)
(五)归纳小结(3点+1个)
(六)课后作业(课本P8-2,3,8,13)
四、教学过程六环节
问题 :一艘轮船在静水中的最大航速是20千米/时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少
附带说明:
2、类似,应用分式表示的实际问题待学习 分式的加减乘除乘方运算后再处理,安排在第9课时进行
1、章头问题移到分式方程处理
(共18课时)
16.1 分式 4课时
16.2 分式的运算 7课时
16.3 分式方程 5课时
小结与复习 2课时
(教师用书安排14课时)
(一)课时安排
(二)课标要求
1.抽象出分式概念;
2.类比分数的基本性质,了解分式的基本性质;掌握分式的约分和通分法则
3.类比分数的四则运算法则,探究分式的四则运算,掌握这些运算法则;
4.结合分式的运算,将指数的讨论范围从正整数扩大到全体整数,构建和发展相联系的知识体系;
5.结合分析和解决实际问题,讨论可化为一元一次方程的分式方程,掌握这种方程的解法,体会解方程中的化归思想;利用分式方程解决实际问题,体会建模思想.
(三)教材简析
分数的类比--------分式学习的引路人
整式相关知识------分式学习必备基础
分式是分数、整式相关知识的应用与延伸
第一节 分式是整章的理论基础部分;
第二节 分式的运算是第一节理论的实践阶段, 是整章的核心;
第三节 分式方程是对分式的发展,其解法及应用充分体现了“化归”与“建模”两类重要思想.
让学生充分动起来
观察、类比、猜想、尝试(思维活动)
发现法则、理解法则、应用法则
发展学生的合情推理能力
对算理的理解、代数表达、运算能力的培养
运算复杂、出错机会增多
控制好题目的难度,不要盲目加大运算量
(四)教学建议
第1课时 §16.1.1 从分数到分式
第2课时 §16.1.2 分式的基本性质
第3课时 §16.1.2 分式的约分
第4课时 §16.1.2 分式的通分
第5课时 §16.2.1 分式的乘除
第6课时 §16.2.1 分式的乘方
第7课时 §16.2.2 分式的加减
第8课时 §16.2.2 分式的混合运算
第9课时 §16.2.2 分式的应用
第10课时 §16.2.3 负整数指数幂
第11课时 §16.2.3 科学记数法
第12课时 §16.3 分式方程
第13课时 §16.3 分式方程(2)
第14课时 §16.3 分式方程的应用(1)
第15课时 §16.3 分式方程的应用(2)
第16课时 §16.3 分式方程的应用(3)
第17课时 《分式》小结与复习(1)
第18课时 《分式》小结与复习(2)
第十六章 分式课时计划
第1课时
教学目标
1.了解分式的概念;
2.理解并能熟练分式有意义的条件,分式的值为零的条件.
重点:分式的概念,
分式有意义、分式的值为零的条件.
难点:熟练求出分式有意义、分式的值为零的条件.
利用分式与分数有许多类似之处,从分数入手,研究出分式的有关概念,同时还要讲清分式与分数的联系与区别.
突破难点的方法:
教学重点、难点
第1课时 16.1.1 从分数到分式
问题情景
形成概念
反馈训练
归纳小结
教学设计框图
复习旧知
类比分数知识
形成分式概念
总结、概括
提出问题
(一)问题情景(复习+问题)
(二)形成概念(类比+归纳)
(三)例题设计(原1+补3)
(四)配套练习(课本P4+补充)
(五)归纳小结(3点+2个)
(六)课后作业(课本P8-2,3,8,13)
教学过程六环节
我们学过的代数式中有单项式、多项式、整式,请你判定下列说法是否正确
(1)2x是单项式,也是整式 ( )
(2) 和0都是单项式,也都是整式 ( )
(3)2x-1是多项式,也是整式 ( )
(4) 是多项式,也是整式 ( )
单项式、多项式统称整式
(一)问题情景
整式
多项式
单项式、多项式统称整式
单项式
(5) 是单项式,也是整式 ( )
(6) 是多项式,也是整式 ( )
既不是单项式又不是多项式,即不是整式的另一类式子----新旧知识的碰撞
1.长方形的面积为10cm ,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______;
S
a
实际问题(课本P2)
2.把体积为200cm 的水倒入底面积为
33cm 的圆柱形容器中,水面高度为
_____cm;把体积为V的水倒入底面积为S
的圆柱形容器中,水面高度为______;
V
S
观察式子 和 , 和 ,辨析它们的相同点和不同点.
都具有分数的形式
相同点
不同点
(观察分母)
分母中有无字母
辨析、思考
两个整式相除的商,分数线可以理解为除号
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式。其中A叫做分式的分子,B为分式的分母。
注意:分式是不同于整式的另一类有理式,且分母中含有字母是分式的一大特点。
(二)形成概念
整式
多项式
单项式
分式
有理式
例1(补充)下面的式子哪些是分式?
(三)例题设计
探究(1)(补充)
思考1 根据下列 的值填表.
……
……
……
……
……
……
0
1
问题: 分式 在什么条件下有意义?
结论:(1)分式中B≠0时,分式 有意义;
(2)分式中B=0,分式 无意义.
该怎样做?
变式练习 若把题目要求改为:“当 取何值时下列分式无意义?”
例2 (补充)当x取什么值时,下列分式有意义?
; (2) ;
(3) ; (4) .
(三)例题设计
思考2 分式 在什么条件下值为0?
归纳 分式的值要为0,需满足的条件是:分子的值等于0且分母值不为0.
仅仅是 就可以了吗?
例3(补充)当 是什么值时,分式的 值是0?
探究(2)
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
例4(补充).已知分式 ,
(3) 当x为何值时,分式的值为零
三种形式
的值为负;
的值为正.
当x 时,
例5(补充)当x 时,
探究(3)附加问题
思考3 分式 在什么条件下值为正?
分式 在什么条件下值为负?
归纳 (1)当A、B同号时,分式 的值为正;
(2)当A、B同号时,分式 的值为负.
1.列式表示下列各量:
(1)某村有n个人,耕地40公顷,人均耕地
面积为_____________公顷;
(2)△ABC的面积为S,BC边长为a,
高AD为_____________;
(3)一辆汽车行驶 千米用 小时,它的平均
速度为____千米/时;一列火车行驶 千米比
这辆汽车少用t小时,它的平均车速为____千米/时.
课本P4 练习 1-3
(四)配套练习(课本P4+例1+补充)
(课本P3例1-当作练习)
练习:下列各式中,无论x取何值,分式都有意义的是( )
C.
A.
B.
D.
(补充)
★ 学习内容:分式的概念 数学思想:类比
1.分式 有意义的条件是__________.
3.分式 值为0的条件是_____________.
2.分式 无意义的条件是__________.
4.分式 值为正的条件是_____________.
5.分式 值为负的条件是_____________.
(五)归纳小结(3个+2点)
分式有意义的条件:
分式的分母不等于零
分式的值为零的条件:
分式的分子等于零
且分母不等于零
分式无意义的条件:
分式的分母等于零
分式的值为正或负的条件:
同号得正,异号得负
(六)课后作业
课本P8-1(直接写在课本) 课本P8-2,3,13
(一)创设情景(复习+问题)
(二)形成概念(类比+归纳)
(三)例题设计(原1+补3)
(四)配套练习(课本P4+补充)
(五)归纳小结(3点+1个)
(六)课后作业(课本P8-2,3,8,13)
四、教学过程六环节
问题 :一艘轮船在静水中的最大航速是20千米/时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少
附带说明:
2、类似,应用分式表示的实际问题待学习 分式的加减乘除乘方运算后再处理,安排在第9课时进行
1、章头问题移到分式方程处理
