5.2运动的合成与分解 同步训练(word版含答案)
文档属性
| 名称 | 5.2运动的合成与分解 同步训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 454.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-10 16:29:33 | ||
图片预览




文档简介
5.2运动的合成与分解
一、单选题
已知河水的流速为ν1,小船在静水中的速度为ν2,且ν2>ν1,下面用小箭头表示小船船头的指向,则下图中能正确反映小船用最短时间渡河、最短位移渡河的情景分别是(??? )
???????
A. ①② B. ①⑤ C. ④⑤ D. ②③
如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面斜向右上方以速度ν匀速运动,运动中始终保持悬线竖直,下列说法正确的是(??? )
A. 橡皮的速度大小为2ν
B. 橡皮的速度大小为3ν
C. 橡皮的速度与水平方向成30°角
D. 橡皮的速度与水平方向成45°角
如图所示,蜡烛块可以在竖直玻璃管内的水中匀速上升,若在蜡烛块从A点开始匀速上升的同时,玻璃管水平向右做匀速直线运动,蜡烛块最终达到C点.蜡烛块从A点到C点的运动轨迹可能是图中的(????)
A. 曲线1 B. 曲线2 C. 直线3 D. 曲线4
如下图所示,有人在河面上方20m的岸上用跨过定滑轮的长绳拴住一条小船,开始时绳与水面的夹角为30°.人以恒定的速率ν=3m/s拉绳使小船靠岸,那么(??? )
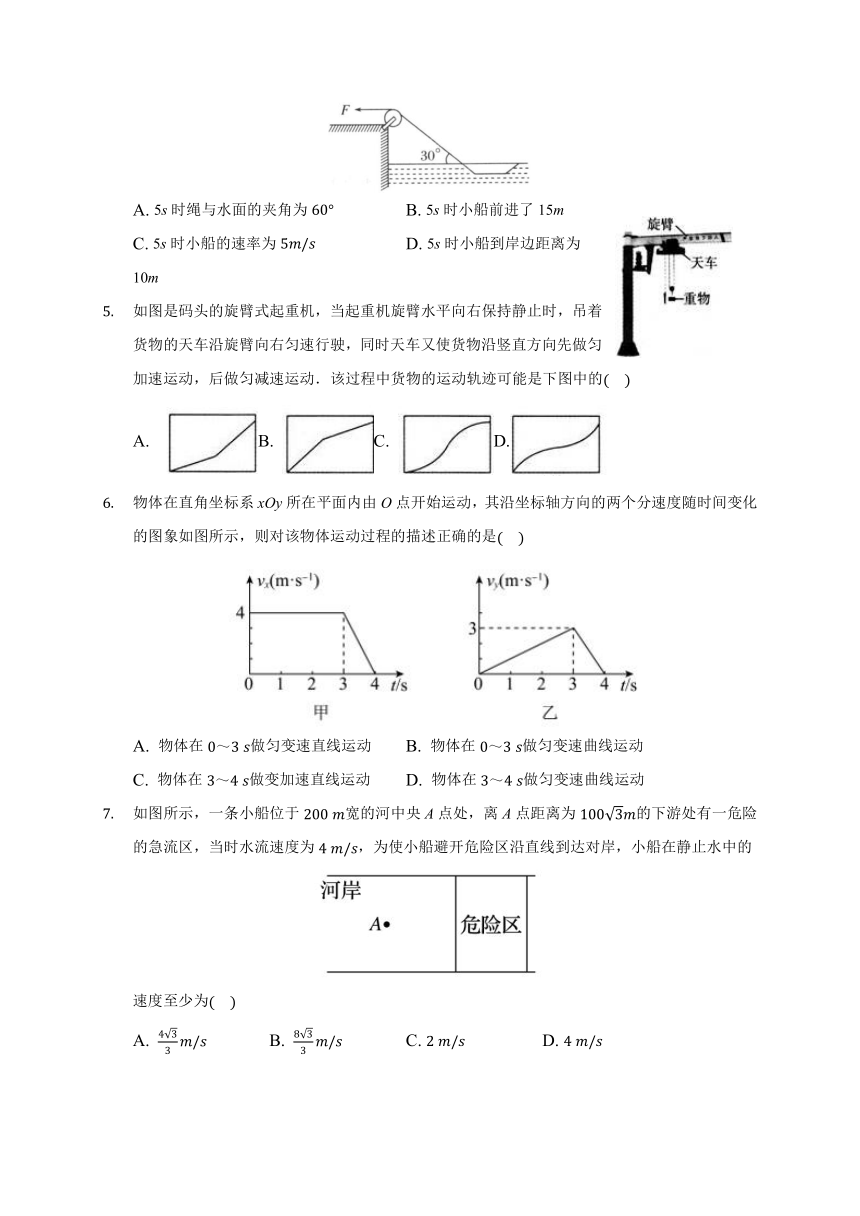
A. 5s时绳与水面的夹角为60° B. 5s时小船前进了15m
C. 5s时小船的速率为5m/s D. 5s时小船到岸边距离为10m
如图是码头的旋臂式起重机,当起重机旋臂水平向右保持静止时,吊着货物的天车沿旋臂向右匀速行驶,同时天车又使货物沿竖直方向先做匀加速运动,后做匀减速运动.该过程中货物的运动轨迹可能是下图中的(????)
A. B. C. D.
物体在直角坐标系xOy所在平面内由O点开始运动,其沿坐标轴方向的两个分速度随时间变化的图象如图所示,则对该物体运动过程的描述正确的是(????)
A. 物体在0~3?s做匀变速直线运动 B. 物体在0~3?s做匀变速曲线运动
C. 物体在3~4?s做变加速直线运动 D. 物体在3~4?s做匀变速曲线运动
如图所示,一条小船位于200?m宽的河中央A点处,离A点距离为1003m的下游处有一危险的急流区,当时水流速度为4?m/s,为使小船避开危险区沿直线到达对岸,小船在静止水中的速度至少为(????)
A. 433m/s B. 833m/s C. 2?m/s D. 4?m/s
小船匀速渡河,已知船在静水中的速度为v1=10m/s,水流速度为v2=4m/s,河宽为d=120m,在船头方向保持不变的情况下,小船渡河时间为t=20s,则以下判断一定正确的是(????)
A. 小船的位移恰好垂直于河岸
B. 小船船头与河岸夹角为θ=37°指向上游方向
C. 小船渡河位移大小为2052m
D. 小船到达对岸时可能在出发点下游240m处
某人划船横渡一条河,河水流速处处相同且恒定,船的划行速率恒定。此人过河的最短时间为t1;若此人用最短的位移过河,则所需时间为t2。已知船的划行速度大于水速,则船的滑行速率与水流速率之比为(? )
A. t2t22?t12 B. t2t1 C. t1t12?t22 D. t1t2
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则(??? )
A. 船的加速度为
B. 船的加速度为F?fm
C. 人拉绳行走的速度为v
D. 人拉绳行走的速度为
如图所示,若小船渡河时船头指向③方向,则所用时间为100?s。已知小船在静水中的速度为2?m/s,②方向与河岸成60°角,河水的流速为4m/s,则(????)。
A. 河的宽度为400?m
B. 在小船渡河过程中船头指向③方向时,小船到达对岸的位置与出发点间的距离为400m
C. 在小船渡河过程中船头指向②方向时,渡河的位移最小
D. 在小船渡河过程中船头指向④方向时,船的实际速度可以达到3.5?m/s
质量为1kg的物体在水平面内运动,已知该物体在两个互相垂直方向上的分运动的速度—时间图像分别如图甲、乙所示,则下列说法正确的是(????)
A. 2s末物体速度大小为7m/s
B. 物体所受的合外力大小为3N
C. 物体的初速度大小为5m/s
D. 物体初速度的方向与合外力方向垂直,做匀变速曲线运动
二、多选题
一只小船渡河,水流速度各处相同且恒定不变,方向平行于岸边.小船相对于水分别做匀加速、匀减速、匀速直线运动,其运动轨迹如图所示.船相对于水的初速度大小均相同,且方向垂直于河岸,船在渡河过程中船头方向始终不变.由此可知(????)
A. 小船沿三条不同轨迹渡河的时间相同
B. 沿AC轨迹渡河所用时间最短
C. 沿AC和AD轨迹小船都是做匀变速运动
D. AD是匀减速运动的轨迹
(多选)如下图所示,一人以恒定速度ν0通过光滑轻质定滑轮竖直向下拉绳使小车在水平面上运动,当运动到绳与水平方向成45°角时(??? )
A. 小车运动的速度为12ν0 B. 小车运动的速度为2ν0
C. 小车在水平面上做加速运动 D. 小车在水平面上做减速运动
物块B套在倾斜杆上,并用轻绳与物块A相连,今使物块B沿杆由点M匀速下滑到N点,运动中连接A、B的轻绳始终保持绷紧状态,在下滑过程中,下列说法不正确的是(????)
A. 物块A的速度先变大后变小
B. 绳上的拉力先大于物体A的重力,再小于物体A的重力
C. 物块A先处于超重状态再处于失重状态
D. 物块A始终处于超重状态
如图所示,套在竖直细杆上的轻环A由跨过定滑轮的不可伸长的轻绳与重物B相连,施加外力让A沿杆以速度v匀速上升,从图中M位置上升至与定滑轮的连线处于水平N位置,已知AO与竖直杆成θ角,则(????)
A. 刚开始时B的速度vB=vcosθ
B. 刚开始时B的速度vB=vcosθ
C. A匀速上升时,重物B减速下降
D. 重物B下降过程,绳对B的拉力小于B的重力
(多选)一根细绳通过定滑轮且两端分别系着A和B两物体,如下图所示,物体A在外力作用下,向左以vA匀速运动,当连A的绳子与水平方向成α角,连B的绳子与水平方向成β角时,B物体的速度为vB,则(???)
A. A物体的速度vA与B物体的速度vB的大小相等
B. A物体的速度vA与B物体的速度vB的大小关系满足νBcosβ=νAcosα
C. 此后B物体以速度vB做匀速运动
D. 此后B物体的速度越来越大,所以做加速运动
如图甲、乙所示,河的宽度为d,船在静水中的速率为v1,水流速为v2,现以甲、乙两种方式渡河,则下列说法正确的是
A. 甲比乙渡河时间长
B. 渡河最短时间为dv1
C. 若v1D. 若v1>v2,如图乙,则渡河时间为dv1cosθ
三、填空题
如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,当A物体以速度v向左运动时,系A、B的绳分别与水平方向成α、β角,此时B物体的速度大小为______,方向______.
一只船在40m宽的河中横渡,水流速度是3m/s,船在静水中的航速是4m/s。现欲使小船以最短时间渡过河去,则应使船头方向______河岸(填“垂直”或“不垂直”)行驶,过河时间为______s,过河距离为______m。
如图,河宽L=60m,一只小船在河的正中央航行,经过O点时发现在距船S=40m的下游有一瀑布,为了使小船在A点安全靠岸,在O点立即调整好船头的指向,不至被冲进瀑布中.若河水的流速大小恒为5m/s,则小船的最小航行速率为______ m/s.若河水的流速与到河岸的最短距离x成正比,即v水=kx(x≤L2,k为一常量),小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,则小船在平行河岸方向做______ 运动.
答案解析
1.C
【解析】船的实际速度是v1和v2的合速度,v1与河岸平行,对渡河时间没有影响,所以v2与河岸垂直即船头指向对岸时,渡河时间最短,为tmin=dv2,式中d为河宽,此时合速度与河岸成一定夹角,船的实际路线应为④所示.最短位移即为d,应使合速度垂直河岸,则v2应指向河岸上游,实际路线为⑤所示.故C正确,ABD错误。故选C。
2.B
【解析】
橡皮参与了平行于斜面方向的匀速直线运动和竖直方向上的匀速直线运动,两个分速度大小相等,都为v,
根据平行四边形定则知:v合=2vcos30°=3v.合速度的方向与水平方向的夹角为60°,故B正确,ACD错误。故选B。
3.C
【解析】当合速度的方向与合力(合加速度)的方向不在同一条直线上,物体将做曲线运动,且轨迹夹在速度与合力(合加速度)方向之间,轨迹的凹向大致指向合力的方向。?
而本题两个方向均做匀速直线运动,因此蜡块将沿着合速度的方向做匀速直线运动,故C正确,ABD错误。?
故选:C。
4.C
【解析】AD、如图
由几何关系可知,开始时河面上的绳长为?sin30?=40m;此时船离岸的距离x1=203m;5s后,绳子向左移动了vt=15m,则河面上绳长为40m?15m=25m;则此时,小船离河边的距离为:x2=252?202m=15m,5s时绳与水面的夹角为α,则有:tanα=2015,解得:α=53°,故AD错误;
B、5s时刻小船前进的距离为:x=203m?15m=19.6m,故B错误;
C、船的速度为合速度,由绳收缩的速度及绳摆动的速度合成得出,则由几何关系可知,cosα=35,则船速v船=vcosα=5m/s,故C正确;故选:C。
5.C
【解析】货物在水平方向上做匀速直线运动,竖直方向上先做匀加速直线运动,加速度方向向上,因为合加速度的方向竖直向上,与合速度不在同一条直线上,合运动的轨迹为曲线。因为加速度的方向(即合力的方向)大致指向轨迹凹的一向,即先向上弯曲;然后货物在竖直方向做减速运动,同上分析可知,在后一段弯曲的方向向下,故ABD错误,故C正确。
故选C。
6.B
【解析】AB.物体在0~3s内,x轴方向做匀速直线运动,y轴方向做匀加速直线运动,所以合初速度与加速度不共线,物体的轨迹为曲线,且加速度恒定,所以是匀变速曲线运动,故A错误;B正确;
CD.物体在3~4s内两个方向的分运动都是匀减速运动,在3s末,合速度v与水平方向夹角为37°,ax=?4m/s2,ay=?3m/s2,合加速度方向与水平方向成37°角且与速度方向相反,则做匀减速直线运动,故CD错误。故选B。
7.C
【解析】小船刚好避开危险区域时,小船合运动方向与水流方向的夹角设为θ,如图所示:
则tan?θ=1001003=33,则θ=30°,当船头垂直合运动方向渡河时,小船在静水中的速度最小,在静水中的最小速度vmin=v水sin?30°=2?m/s,故C正确,ABD错误。故选C。
8.D
【解析】根据题意:河宽为d=120m,在船头方向保持不变的情况下,小船渡河时间为t=20s,那么船在垂直河岸方向的速度大小为v1=dt=12020m/s=6m/s,由于船在静水中的速度为v1=10m/s,根据矢量的合成法则,则船在平行于水流方向分速度大小为v2=8m/s
A.由上分析可知,船的位移不可能垂直河岸,故A错误;
B.当船在平行于水流方向分速度方向逆着水流方向时,则船头与河岸夹角才为θ=37°指向上游方向;若船在平行于水流方向分速度方向顺着水流方向时,则船头与河岸夹角为θ=37°指向下游方向,故B错误;
C.当偏向上游时,则位移为s=1202+[(8?4)×20]2m=2052m;
若偏向下游时,则位移为s'=1202+[(8+4)×20]2m=1205m,故C错误;
D.由上分析可知,到达对岸时可能在出发点下游x=(8+4)×20m=240m处,故D正确。故选:D。
9.A
【解析】设河宽为d,设船在静水中的速率为v1,水流速为v2。当最短时间过河时,静水速与河岸垂直有:t1=dv1①
当最小位移过河时如图所示:
v合=v12?v22,则:t2=dv合=dv12?v22②
联立①②计算得出:v1v2=t2t22?t12。
故A正确,BCD错误。故选A。
10.A
【解析】AB、对小船受力分析,如下图所示,则有Fcosθ?f=ma,因此船的加速度大小为a=Fcosθ?fm,故A正确,B错误;
CD、船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度。如图所示根据平行四边形定则有,v人=vcosθ.故CD错误;故选:A。
11.C
【解析】A.当船头垂直指向对岸时,渡河时间最短,小船渡河时船头指向③方向,则所用时间最短为100?s,有:d=v船·tmin=200m,故A错误;
B.在小船渡河过程中船头指向③方向时,沿河岸的距离为:L=v水·tmin=400m,故小船到达对岸的位置与出发点间的距离为:s=d2+L2=2005m,故B错误;
C.因为v船D.当小船渡河过程中船头指向④方向时,根据平行四边形定则可知,船的实际速度大于水速的4m/s,故D错误。故选:C。
12.D
【解析】A、据题意,物体在两个互相垂直方向上运动,即x与y方向垂直,且质点在x方向做初速度为零的匀加速直线运动,在y方向做匀速直线运动,2s末,vx=3m/s,vy=4m/s,
因而v=vx2+vy2=5m/s,故A错误;
B、ax=ΔvΔt=1.5m/s2,ay=0
根据牛顿第二定律
Fx=max=1×1.5N=1.5N
Fy=0
因而F=1.5N,故B错误;
C、t=0时,vx=0,vy=4m/s
因而v0=4m/s,故C错误;
D、由于初速度v0=4m/s沿y方向,F=1.5N沿x方向,速度方向与合力方向不在同一条直线上,故物体做匀变速曲线运动,故D正确;故选:D。
13.BCD
【解析】A.船相对于水的初速度大小均相同,方向垂直于岸边,因运动的性质不同,则渡河时间也不同,故A错误;
CD.沿AB轨迹,合速度不变,说明船相对于水的速度不变;沿AC轨迹运动,由图可知,弯曲的方向向上,所以沿垂直于河岸的方向做加速运动;而沿AD轨迹运动,弯曲的方向向下,可知小船沿垂直于河岸的方向做减速运动,故CD正确;
B.沿AC轨迹,船是匀加速运动,则船到达对岸的速度最大,所以使用的时间最短,故B正确。故选BCD。
14.BC
【解析】AB? 将小车速度沿绳方向与垂直绳方向进行分解,如下图所示
人拉绳的速度与小车沿绳方向的分速度大小是相等的,则νcos45°=ν0,可得ν=ν0cos45?=2ν0,B正确,A错误;
CD.小车向左运动,绳与水平方向的夹角越来越大,设夹角为α,由ν=ν0cosα知,ν越来越大,则小车在水平面上做加速运动,C正确,D错误.故选BC.
15.ABC
【解析】
A.将B的速度分解为沿绳子方向和垂直于绳子方向,如图:
根据平行四边形定则,沿绳子方向的速度为
可知θ在增大到90°的过程中,A的速度方向向下,且逐渐减小;由图可知,当B到达P点时,B与滑轮之间的距离最短,θ=90°,A的速度等于0,随后A向上运动,且速度增大。所以在B沿杆由点M匀速下滑到N点的过程中,A的速度先向下减小,然后向上增大,故A错误;
BCD.物体A向下做减速运动和向上做加速运动的过程中,加速度的方向都向上,所以A始终处于超重状态,绳上的拉力始终大于物体A的重力,故D正确,BC错误。故选ABC。
16.BC
【解析】
AB、对于A它的速度如图中标出的v,这个速度是A的合速度,其分速度分别是va,vb;其中va等于B的速度vB(同一根绳子,大小相同),刚开始时B的速度为vB=va=vcosθ,所以A错误,B正确;
CD、根据vB=vcosθ,A匀速上升时,夹角θ增大,因此B做减速运动,由牛顿第二定律,可知绳对B的拉力大于B的重力,故D错误,C正确;故选:BC。
17.BD
【解析】对A物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vAcosα;对B物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vBcosβ,由于沿着绳子方向速度大小相等,所以则有vAcosα=vBcosβ,因此vB=cosαcosβvA,α角越来越小,β角越来越大,所以此后B物体的速度越来越大,所以做加速运动,故AC错误,BD正确。故选BD。
18.BC
【解析】A、甲渡河时间为dv1,乙渡河时间为dv1sinθ,故A错误;
B、当船头方向正对河岸时,渡河时间最短,为dv1,故B正确;
C、若要想到达正对岸,应该按照图乙方式渡河,则有v1cosθ=v2,得v1>v2,若v1D、根据A选项可知,图乙渡河时间为dv1sinθ,故D错误。故选BC。
19.cosαcosβv;水平向右
【解析】对A物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vAcosα;对B物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vBcosβ,由于沿着绳子方向速度大小相等,所以则有vcosα=vBcosβ,因此vB=cosαcosβv,且向右运动;
故答案为:cosαcosβv;水平向右.
分别对A、B物体速度沿着绳子方向与垂直绳子方向进行分解,根据三角函数关系及沿着绳子方向速度大小相等,可知两物体的速度大小关系.
考查学会对物体进行运动的分解,涉及到平行四边形定则与三角函数知识,同时本题的突破口是沿着绳子的方向速度大小相等.
20.垂直? 10? 50
【解析】将小船的运动分解为垂直河岸和沿河岸方向,在垂直于河岸的方向上,河宽一定,当在该方向上的速度最大时,渡河时间最短。可知当船头方向垂直河岸,在该方向上的速度等于静水航速,时间最短,即为:t=dvc=404=10s。
该过程中船沿河岸方向的位移为:y=vs?t=3×10=30m
所以船的总位移为:s=x2+y2=402+302=50m.故答案为:垂直,10,50
21.3;匀减速
【解析】解:要使小船避开危险区沿直线到达对岸,则有合运动的最大位移为OA=302+402m=50m.
根据题目中的图,那个30m和40m要构成一个直角三角形的两条边,那么斜边就是50m了,那么正弦就是35,
这是一个路程的三角形,再找一个速度的三角形,就是船速和水流速为直角边的,水流速是5m/s,而且这两个是相似三角形,
所以那个正弦乘以5m/s就行了,5×35=3m/s,
因此船的速度最小速率为3m/s,
若河水的流速与到河岸的最短距离x成正比,小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,
v水=kx=kv船t,则小船在平行河岸方向速度在均匀减小,则做匀减速直线运动,故答案为:3,匀减速.
一、单选题
已知河水的流速为ν1,小船在静水中的速度为ν2,且ν2>ν1,下面用小箭头表示小船船头的指向,则下图中能正确反映小船用最短时间渡河、最短位移渡河的情景分别是(??? )
???????
A. ①② B. ①⑤ C. ④⑤ D. ②③
如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面斜向右上方以速度ν匀速运动,运动中始终保持悬线竖直,下列说法正确的是(??? )
A. 橡皮的速度大小为2ν
B. 橡皮的速度大小为3ν
C. 橡皮的速度与水平方向成30°角
D. 橡皮的速度与水平方向成45°角
如图所示,蜡烛块可以在竖直玻璃管内的水中匀速上升,若在蜡烛块从A点开始匀速上升的同时,玻璃管水平向右做匀速直线运动,蜡烛块最终达到C点.蜡烛块从A点到C点的运动轨迹可能是图中的(????)
A. 曲线1 B. 曲线2 C. 直线3 D. 曲线4
如下图所示,有人在河面上方20m的岸上用跨过定滑轮的长绳拴住一条小船,开始时绳与水面的夹角为30°.人以恒定的速率ν=3m/s拉绳使小船靠岸,那么(??? )
A. 5s时绳与水面的夹角为60° B. 5s时小船前进了15m
C. 5s时小船的速率为5m/s D. 5s时小船到岸边距离为10m
如图是码头的旋臂式起重机,当起重机旋臂水平向右保持静止时,吊着货物的天车沿旋臂向右匀速行驶,同时天车又使货物沿竖直方向先做匀加速运动,后做匀减速运动.该过程中货物的运动轨迹可能是下图中的(????)
A. B. C. D.
物体在直角坐标系xOy所在平面内由O点开始运动,其沿坐标轴方向的两个分速度随时间变化的图象如图所示,则对该物体运动过程的描述正确的是(????)
A. 物体在0~3?s做匀变速直线运动 B. 物体在0~3?s做匀变速曲线运动
C. 物体在3~4?s做变加速直线运动 D. 物体在3~4?s做匀变速曲线运动
如图所示,一条小船位于200?m宽的河中央A点处,离A点距离为1003m的下游处有一危险的急流区,当时水流速度为4?m/s,为使小船避开危险区沿直线到达对岸,小船在静止水中的速度至少为(????)
A. 433m/s B. 833m/s C. 2?m/s D. 4?m/s
小船匀速渡河,已知船在静水中的速度为v1=10m/s,水流速度为v2=4m/s,河宽为d=120m,在船头方向保持不变的情况下,小船渡河时间为t=20s,则以下判断一定正确的是(????)
A. 小船的位移恰好垂直于河岸
B. 小船船头与河岸夹角为θ=37°指向上游方向
C. 小船渡河位移大小为2052m
D. 小船到达对岸时可能在出发点下游240m处
某人划船横渡一条河,河水流速处处相同且恒定,船的划行速率恒定。此人过河的最短时间为t1;若此人用最短的位移过河,则所需时间为t2。已知船的划行速度大于水速,则船的滑行速率与水流速率之比为(? )
A. t2t22?t12 B. t2t1 C. t1t12?t22 D. t1t2
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则(??? )
A. 船的加速度为
B. 船的加速度为F?fm
C. 人拉绳行走的速度为v
D. 人拉绳行走的速度为
如图所示,若小船渡河时船头指向③方向,则所用时间为100?s。已知小船在静水中的速度为2?m/s,②方向与河岸成60°角,河水的流速为4m/s,则(????)。
A. 河的宽度为400?m
B. 在小船渡河过程中船头指向③方向时,小船到达对岸的位置与出发点间的距离为400m
C. 在小船渡河过程中船头指向②方向时,渡河的位移最小
D. 在小船渡河过程中船头指向④方向时,船的实际速度可以达到3.5?m/s
质量为1kg的物体在水平面内运动,已知该物体在两个互相垂直方向上的分运动的速度—时间图像分别如图甲、乙所示,则下列说法正确的是(????)
A. 2s末物体速度大小为7m/s
B. 物体所受的合外力大小为3N
C. 物体的初速度大小为5m/s
D. 物体初速度的方向与合外力方向垂直,做匀变速曲线运动
二、多选题
一只小船渡河,水流速度各处相同且恒定不变,方向平行于岸边.小船相对于水分别做匀加速、匀减速、匀速直线运动,其运动轨迹如图所示.船相对于水的初速度大小均相同,且方向垂直于河岸,船在渡河过程中船头方向始终不变.由此可知(????)
A. 小船沿三条不同轨迹渡河的时间相同
B. 沿AC轨迹渡河所用时间最短
C. 沿AC和AD轨迹小船都是做匀变速运动
D. AD是匀减速运动的轨迹
(多选)如下图所示,一人以恒定速度ν0通过光滑轻质定滑轮竖直向下拉绳使小车在水平面上运动,当运动到绳与水平方向成45°角时(??? )
A. 小车运动的速度为12ν0 B. 小车运动的速度为2ν0
C. 小车在水平面上做加速运动 D. 小车在水平面上做减速运动
物块B套在倾斜杆上,并用轻绳与物块A相连,今使物块B沿杆由点M匀速下滑到N点,运动中连接A、B的轻绳始终保持绷紧状态,在下滑过程中,下列说法不正确的是(????)
A. 物块A的速度先变大后变小
B. 绳上的拉力先大于物体A的重力,再小于物体A的重力
C. 物块A先处于超重状态再处于失重状态
D. 物块A始终处于超重状态
如图所示,套在竖直细杆上的轻环A由跨过定滑轮的不可伸长的轻绳与重物B相连,施加外力让A沿杆以速度v匀速上升,从图中M位置上升至与定滑轮的连线处于水平N位置,已知AO与竖直杆成θ角,则(????)
A. 刚开始时B的速度vB=vcosθ
B. 刚开始时B的速度vB=vcosθ
C. A匀速上升时,重物B减速下降
D. 重物B下降过程,绳对B的拉力小于B的重力
(多选)一根细绳通过定滑轮且两端分别系着A和B两物体,如下图所示,物体A在外力作用下,向左以vA匀速运动,当连A的绳子与水平方向成α角,连B的绳子与水平方向成β角时,B物体的速度为vB,则(???)
A. A物体的速度vA与B物体的速度vB的大小相等
B. A物体的速度vA与B物体的速度vB的大小关系满足νBcosβ=νAcosα
C. 此后B物体以速度vB做匀速运动
D. 此后B物体的速度越来越大,所以做加速运动
如图甲、乙所示,河的宽度为d,船在静水中的速率为v1,水流速为v2,现以甲、乙两种方式渡河,则下列说法正确的是
A. 甲比乙渡河时间长
B. 渡河最短时间为dv1
C. 若v1
三、填空题
如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,当A物体以速度v向左运动时,系A、B的绳分别与水平方向成α、β角,此时B物体的速度大小为______,方向______.
一只船在40m宽的河中横渡,水流速度是3m/s,船在静水中的航速是4m/s。现欲使小船以最短时间渡过河去,则应使船头方向______河岸(填“垂直”或“不垂直”)行驶,过河时间为______s,过河距离为______m。
如图,河宽L=60m,一只小船在河的正中央航行,经过O点时发现在距船S=40m的下游有一瀑布,为了使小船在A点安全靠岸,在O点立即调整好船头的指向,不至被冲进瀑布中.若河水的流速大小恒为5m/s,则小船的最小航行速率为______ m/s.若河水的流速与到河岸的最短距离x成正比,即v水=kx(x≤L2,k为一常量),小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,则小船在平行河岸方向做______ 运动.
答案解析
1.C
【解析】船的实际速度是v1和v2的合速度,v1与河岸平行,对渡河时间没有影响,所以v2与河岸垂直即船头指向对岸时,渡河时间最短,为tmin=dv2,式中d为河宽,此时合速度与河岸成一定夹角,船的实际路线应为④所示.最短位移即为d,应使合速度垂直河岸,则v2应指向河岸上游,实际路线为⑤所示.故C正确,ABD错误。故选C。
2.B
【解析】
橡皮参与了平行于斜面方向的匀速直线运动和竖直方向上的匀速直线运动,两个分速度大小相等,都为v,
根据平行四边形定则知:v合=2vcos30°=3v.合速度的方向与水平方向的夹角为60°,故B正确,ACD错误。故选B。
3.C
【解析】当合速度的方向与合力(合加速度)的方向不在同一条直线上,物体将做曲线运动,且轨迹夹在速度与合力(合加速度)方向之间,轨迹的凹向大致指向合力的方向。?
而本题两个方向均做匀速直线运动,因此蜡块将沿着合速度的方向做匀速直线运动,故C正确,ABD错误。?
故选:C。
4.C
【解析】AD、如图
由几何关系可知,开始时河面上的绳长为?sin30?=40m;此时船离岸的距离x1=203m;5s后,绳子向左移动了vt=15m,则河面上绳长为40m?15m=25m;则此时,小船离河边的距离为:x2=252?202m=15m,5s时绳与水面的夹角为α,则有:tanα=2015,解得:α=53°,故AD错误;
B、5s时刻小船前进的距离为:x=203m?15m=19.6m,故B错误;
C、船的速度为合速度,由绳收缩的速度及绳摆动的速度合成得出,则由几何关系可知,cosα=35,则船速v船=vcosα=5m/s,故C正确;故选:C。
5.C
【解析】货物在水平方向上做匀速直线运动,竖直方向上先做匀加速直线运动,加速度方向向上,因为合加速度的方向竖直向上,与合速度不在同一条直线上,合运动的轨迹为曲线。因为加速度的方向(即合力的方向)大致指向轨迹凹的一向,即先向上弯曲;然后货物在竖直方向做减速运动,同上分析可知,在后一段弯曲的方向向下,故ABD错误,故C正确。
故选C。
6.B
【解析】AB.物体在0~3s内,x轴方向做匀速直线运动,y轴方向做匀加速直线运动,所以合初速度与加速度不共线,物体的轨迹为曲线,且加速度恒定,所以是匀变速曲线运动,故A错误;B正确;
CD.物体在3~4s内两个方向的分运动都是匀减速运动,在3s末,合速度v与水平方向夹角为37°,ax=?4m/s2,ay=?3m/s2,合加速度方向与水平方向成37°角且与速度方向相反,则做匀减速直线运动,故CD错误。故选B。
7.C
【解析】小船刚好避开危险区域时,小船合运动方向与水流方向的夹角设为θ,如图所示:
则tan?θ=1001003=33,则θ=30°,当船头垂直合运动方向渡河时,小船在静水中的速度最小,在静水中的最小速度vmin=v水sin?30°=2?m/s,故C正确,ABD错误。故选C。
8.D
【解析】根据题意:河宽为d=120m,在船头方向保持不变的情况下,小船渡河时间为t=20s,那么船在垂直河岸方向的速度大小为v1=dt=12020m/s=6m/s,由于船在静水中的速度为v1=10m/s,根据矢量的合成法则,则船在平行于水流方向分速度大小为v2=8m/s
A.由上分析可知,船的位移不可能垂直河岸,故A错误;
B.当船在平行于水流方向分速度方向逆着水流方向时,则船头与河岸夹角才为θ=37°指向上游方向;若船在平行于水流方向分速度方向顺着水流方向时,则船头与河岸夹角为θ=37°指向下游方向,故B错误;
C.当偏向上游时,则位移为s=1202+[(8?4)×20]2m=2052m;
若偏向下游时,则位移为s'=1202+[(8+4)×20]2m=1205m,故C错误;
D.由上分析可知,到达对岸时可能在出发点下游x=(8+4)×20m=240m处,故D正确。故选:D。
9.A
【解析】设河宽为d,设船在静水中的速率为v1,水流速为v2。当最短时间过河时,静水速与河岸垂直有:t1=dv1①
当最小位移过河时如图所示:
v合=v12?v22,则:t2=dv合=dv12?v22②
联立①②计算得出:v1v2=t2t22?t12。
故A正确,BCD错误。故选A。
10.A
【解析】AB、对小船受力分析,如下图所示,则有Fcosθ?f=ma,因此船的加速度大小为a=Fcosθ?fm,故A正确,B错误;
CD、船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度。如图所示根据平行四边形定则有,v人=vcosθ.故CD错误;故选:A。
11.C
【解析】A.当船头垂直指向对岸时,渡河时间最短,小船渡河时船头指向③方向,则所用时间最短为100?s,有:d=v船·tmin=200m,故A错误;
B.在小船渡河过程中船头指向③方向时,沿河岸的距离为:L=v水·tmin=400m,故小船到达对岸的位置与出发点间的距离为:s=d2+L2=2005m,故B错误;
C.因为v船
12.D
【解析】A、据题意,物体在两个互相垂直方向上运动,即x与y方向垂直,且质点在x方向做初速度为零的匀加速直线运动,在y方向做匀速直线运动,2s末,vx=3m/s,vy=4m/s,
因而v=vx2+vy2=5m/s,故A错误;
B、ax=ΔvΔt=1.5m/s2,ay=0
根据牛顿第二定律
Fx=max=1×1.5N=1.5N
Fy=0
因而F=1.5N,故B错误;
C、t=0时,vx=0,vy=4m/s
因而v0=4m/s,故C错误;
D、由于初速度v0=4m/s沿y方向,F=1.5N沿x方向,速度方向与合力方向不在同一条直线上,故物体做匀变速曲线运动,故D正确;故选:D。
13.BCD
【解析】A.船相对于水的初速度大小均相同,方向垂直于岸边,因运动的性质不同,则渡河时间也不同,故A错误;
CD.沿AB轨迹,合速度不变,说明船相对于水的速度不变;沿AC轨迹运动,由图可知,弯曲的方向向上,所以沿垂直于河岸的方向做加速运动;而沿AD轨迹运动,弯曲的方向向下,可知小船沿垂直于河岸的方向做减速运动,故CD正确;
B.沿AC轨迹,船是匀加速运动,则船到达对岸的速度最大,所以使用的时间最短,故B正确。故选BCD。
14.BC
【解析】AB? 将小车速度沿绳方向与垂直绳方向进行分解,如下图所示
人拉绳的速度与小车沿绳方向的分速度大小是相等的,则νcos45°=ν0,可得ν=ν0cos45?=2ν0,B正确,A错误;
CD.小车向左运动,绳与水平方向的夹角越来越大,设夹角为α,由ν=ν0cosα知,ν越来越大,则小车在水平面上做加速运动,C正确,D错误.故选BC.
15.ABC
【解析】
A.将B的速度分解为沿绳子方向和垂直于绳子方向,如图:
根据平行四边形定则,沿绳子方向的速度为
可知θ在增大到90°的过程中,A的速度方向向下,且逐渐减小;由图可知,当B到达P点时,B与滑轮之间的距离最短,θ=90°,A的速度等于0,随后A向上运动,且速度增大。所以在B沿杆由点M匀速下滑到N点的过程中,A的速度先向下减小,然后向上增大,故A错误;
BCD.物体A向下做减速运动和向上做加速运动的过程中,加速度的方向都向上,所以A始终处于超重状态,绳上的拉力始终大于物体A的重力,故D正确,BC错误。故选ABC。
16.BC
【解析】
AB、对于A它的速度如图中标出的v,这个速度是A的合速度,其分速度分别是va,vb;其中va等于B的速度vB(同一根绳子,大小相同),刚开始时B的速度为vB=va=vcosθ,所以A错误,B正确;
CD、根据vB=vcosθ,A匀速上升时,夹角θ增大,因此B做减速运动,由牛顿第二定律,可知绳对B的拉力大于B的重力,故D错误,C正确;故选:BC。
17.BD
【解析】对A物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vAcosα;对B物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vBcosβ,由于沿着绳子方向速度大小相等,所以则有vAcosα=vBcosβ,因此vB=cosαcosβvA,α角越来越小,β角越来越大,所以此后B物体的速度越来越大,所以做加速运动,故AC错误,BD正确。故选BD。
18.BC
【解析】A、甲渡河时间为dv1,乙渡河时间为dv1sinθ,故A错误;
B、当船头方向正对河岸时,渡河时间最短,为dv1,故B正确;
C、若要想到达正对岸,应该按照图乙方式渡河,则有v1cosθ=v2,得v1>v2,若v1
19.cosαcosβv;水平向右
【解析】对A物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vAcosα;对B物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vBcosβ,由于沿着绳子方向速度大小相等,所以则有vcosα=vBcosβ,因此vB=cosαcosβv,且向右运动;
故答案为:cosαcosβv;水平向右.
分别对A、B物体速度沿着绳子方向与垂直绳子方向进行分解,根据三角函数关系及沿着绳子方向速度大小相等,可知两物体的速度大小关系.
考查学会对物体进行运动的分解,涉及到平行四边形定则与三角函数知识,同时本题的突破口是沿着绳子的方向速度大小相等.
20.垂直? 10? 50
【解析】将小船的运动分解为垂直河岸和沿河岸方向,在垂直于河岸的方向上,河宽一定,当在该方向上的速度最大时,渡河时间最短。可知当船头方向垂直河岸,在该方向上的速度等于静水航速,时间最短,即为:t=dvc=404=10s。
该过程中船沿河岸方向的位移为:y=vs?t=3×10=30m
所以船的总位移为:s=x2+y2=402+302=50m.故答案为:垂直,10,50
21.3;匀减速
【解析】解:要使小船避开危险区沿直线到达对岸,则有合运动的最大位移为OA=302+402m=50m.
根据题目中的图,那个30m和40m要构成一个直角三角形的两条边,那么斜边就是50m了,那么正弦就是35,
这是一个路程的三角形,再找一个速度的三角形,就是船速和水流速为直角边的,水流速是5m/s,而且这两个是相似三角形,
所以那个正弦乘以5m/s就行了,5×35=3m/s,
因此船的速度最小速率为3m/s,
若河水的流速与到河岸的最短距离x成正比,小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,
v水=kx=kv船t,则小船在平行河岸方向速度在均匀减小,则做匀减速直线运动,故答案为:3,匀减速.
