六年级数学下册课件 第5单元鸽巢问题 人教版 42张
文档属性
| 名称 | 六年级数学下册课件 第5单元鸽巢问题 人教版 42张 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 09:56:57 | ||
图片预览







文档简介
(共42张PPT)
鸽
巢
问
题
·六年级下册
犍为县龙孔中心小学
曾秀芳
通过学习,你想解决哪些问题?
通过同学们的回答发现大家最想知道的是:
“鸽巢问题”是怎样的?
这里的“鸽巢”是指什么?
运用“鸽巢问题”能解决哪些问题?
怎样运用“鸽巢问题”解决问题?
3支铅笔放进2个盒子
3支铅笔放进2个盒子
4支铅笔放进3个盒子
第一个盒子里放4支,另外连个盒子里不放。
可以将这种放法记为(4,0,0)。
除了这种放法,还有其他的放法吗?
4支铅笔放进3个盒子
4支铅笔放进3个盒子
四支铅笔放进三个盒子
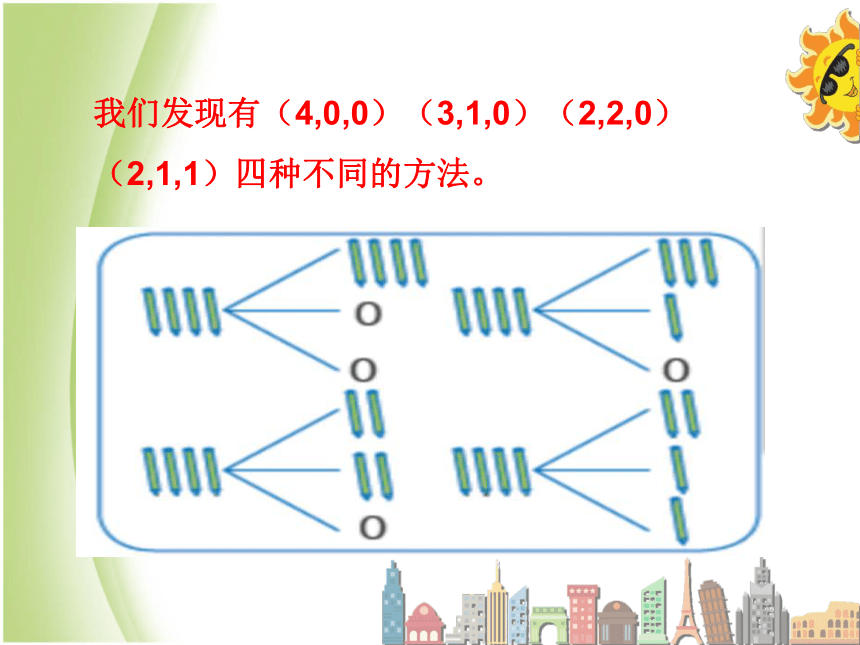
我们发现有(4,0,0)(3,1,0)(2,2,0)(2,1,1)四种不同的方法。
还有不同的放法吗?
通过刚才的操作,你能发现什么?
“总有”是什么意思?
不管怎么放,总有一个盒子里至少有2枝铅笔。
一定有
“至少”有2枝什么意思?
就是不能少于2枝。
上面这样的问题就是“鸽巢问题”,在这里,“4枝铅笔”就是“4个要分放的物体”,“3个盒子”相当于“3个鸽巢”。把此问题用“鸽巢问题”的语言描述就是:把4个物体放进3个鸽巢中,总有一个鸽巢中至少有2个物体。
“鸽巢原理”也称“抽屉原理”,鸽巢可以看作是抽屉。
把5枝铅笔放进4个盒子,总有一个盒子至少要放进几枝铅笔?说一说,并且说一说为什么?
把4枝笔放进3个盒子里,和把5枝笔放进4个盒子里,不管怎么放,总有一个盒子里至少有2枝铅笔。这是我们通过实际操作发现的这个结论。那么,我们能不能找到一种更为直接的方法,只摆一种情况,也能得到这个结论呢?
4支铅笔放进3个盒子
哪一组同学能把你们的想法汇报一下?
我们发现如果每个盒子里放1枝铅笔,最多放3枝,剩下的1枝不管放进哪一个盒子里,总有一个盒子里至少有2枝铅笔。
4支铅笔放进3个盒子
你能结合操作给大家讲一讲吗?
同桌之间说一说自己的想法好吗?
这种分法,实际上是先怎么分的?
平均分。
4支铅笔放进3个盒子
怎样用算式表示这种方法?
(4÷3=1枝……1枝
1+1=2枝)
算式中的两个“1”是什么意思?
为什么要先平均分?
因为先平均分,使每个盒子的笔尽可能少一点,方便找到“至少数”,先平均分,余下1枝,不管放在哪个盒子里,一定会出现“总有一个盒子里至少有2枝”。
这样分,只分一次就能确定总有一个盒子至少有几枝笔了,
同意吗?那么把5枝笔放进4个盒子里呢?
哪位同学能把你的想法汇报一下?
5枝铅笔放在4个盒子里,不管怎么放,总有一个盒子里至少有2枝铅笔。
5枝笔放进4个盒子
把6枝笔放进5个盒子里呢?还用摆吗?
6枝铅笔放在5个盒子里,不管怎么放,总有一个盒子里至少有2枝铅笔。
把7枝笔放进6个盒子里呢?
把8枝笔放进7个盒子里呢?
把9枝笔放进8个盒子里呢?……
铅笔的枝数比盒子数多1,不管怎么放,总有一个盒子里至少有2枝铅笔。
你们的发现和他一样吗
把100枝铅笔放进99个文具盒里会有什么结论?一起说。
你发现什么?
5枝铅笔放进3个盒子呢?你又打算怎样放?
总有一个盒子里至少有2枝还是3枝?为什么?
那么,铅笔的枝数比盒子数量不是只多1呢?还是这种情况吗?
先平均分每个盒子放进1枝笔,余下2只再平均分放进2个不同的盒子里,所以至少2只。
5÷3=1枝……2枝
为什么第二次平均分?
保证“至少”。
只要铅笔数比盒子的数量多,总有一个盒子中至少放进2支铅笔。
“鸽巢原理”(一):把m个物体任意分放进n个鸽巢中(m>n,m和n是非0自然数),那么一定有一个鸽巢中至少放进了2个物体。
你发现什么?
现在我要把把7枝铅笔放进3个盒子。枝数最多的那个盒子至少要放多少枝?
用你喜欢的方法,具体放一放,分一分,画一画,看看会是什么结果。同方同学可以交流。看看至少几枝铅笔会放进同一个盒子?
如果把笔和盒子的数量进一步增加呢?
有更简单的方法吗?需要说明的是数量最多的那个盒子?
(1)7枝笔放进3个盒子,至少几枝放进同一个盒子?
7÷3=2(枝)…1(枝)?
1+1=2(枝)
(2)14枝笔放进4个盒子,至少几枝放进同一个盒子?
14÷4=3(枝)…2(枝)?
3+1=4(枝)
(3)23枝笔放进4个盒子,至少几枝放进同一个盒子?
23÷4=5(枝)…3(枝)?
5+1=6(枝)
对比算式,你发现什么规律?
有没有谁可以用字母来把我们的鸽巢原理表示出来?
要求至少数,都先平均分,再用所得的“商+1”
至少数和余数有没有关系?
与余数无关,不管余多少,都要再平均分,所以就只加1。
物体数÷鸽巢数=商……余数
至少数=商+1
前面我们归纳出了鸽巢原理(一):把m个物体任意分放进n个鸽巢中(m>n,m和n是非0自然数),那么一定有一个鸽巢中至少放进了2个物体。
kn÷n=k……c
(k是正整数,n、c是非0自然数),
至少数=k+1
谁能用自己的话概括我们刚才研究的原理吗?
“鸽巢原理”(二):把多于kn个的物体任意放进n个鸽巢中(k是正整数,n是非0自然数),那么一定有一个鸽巢中至少放进了(k+1)个物体。
谁能用字母把鸽巢原理表示出来?
当c=0时呢?也就是平均分没有余数的时候呢?
至少数该是多少?
课堂小结
通过这节课的学习,你有哪些新的收获呢?
我们学会了简单的鸽巢问题。
可以用动手操作、列举法、画图法来帮助我们分析,也可以用除法的意义来解答。
鸽
巢
问
题
·六年级下册
犍为县龙孔中心小学
曾秀芳
通过学习,你想解决哪些问题?
通过同学们的回答发现大家最想知道的是:
“鸽巢问题”是怎样的?
这里的“鸽巢”是指什么?
运用“鸽巢问题”能解决哪些问题?
怎样运用“鸽巢问题”解决问题?
3支铅笔放进2个盒子
3支铅笔放进2个盒子
4支铅笔放进3个盒子
第一个盒子里放4支,另外连个盒子里不放。
可以将这种放法记为(4,0,0)。
除了这种放法,还有其他的放法吗?
4支铅笔放进3个盒子
4支铅笔放进3个盒子
四支铅笔放进三个盒子
我们发现有(4,0,0)(3,1,0)(2,2,0)(2,1,1)四种不同的方法。
还有不同的放法吗?
通过刚才的操作,你能发现什么?
“总有”是什么意思?
不管怎么放,总有一个盒子里至少有2枝铅笔。
一定有
“至少”有2枝什么意思?
就是不能少于2枝。
上面这样的问题就是“鸽巢问题”,在这里,“4枝铅笔”就是“4个要分放的物体”,“3个盒子”相当于“3个鸽巢”。把此问题用“鸽巢问题”的语言描述就是:把4个物体放进3个鸽巢中,总有一个鸽巢中至少有2个物体。
“鸽巢原理”也称“抽屉原理”,鸽巢可以看作是抽屉。
把5枝铅笔放进4个盒子,总有一个盒子至少要放进几枝铅笔?说一说,并且说一说为什么?
把4枝笔放进3个盒子里,和把5枝笔放进4个盒子里,不管怎么放,总有一个盒子里至少有2枝铅笔。这是我们通过实际操作发现的这个结论。那么,我们能不能找到一种更为直接的方法,只摆一种情况,也能得到这个结论呢?
4支铅笔放进3个盒子
哪一组同学能把你们的想法汇报一下?
我们发现如果每个盒子里放1枝铅笔,最多放3枝,剩下的1枝不管放进哪一个盒子里,总有一个盒子里至少有2枝铅笔。
4支铅笔放进3个盒子
你能结合操作给大家讲一讲吗?
同桌之间说一说自己的想法好吗?
这种分法,实际上是先怎么分的?
平均分。
4支铅笔放进3个盒子
怎样用算式表示这种方法?
(4÷3=1枝……1枝
1+1=2枝)
算式中的两个“1”是什么意思?
为什么要先平均分?
因为先平均分,使每个盒子的笔尽可能少一点,方便找到“至少数”,先平均分,余下1枝,不管放在哪个盒子里,一定会出现“总有一个盒子里至少有2枝”。
这样分,只分一次就能确定总有一个盒子至少有几枝笔了,
同意吗?那么把5枝笔放进4个盒子里呢?
哪位同学能把你的想法汇报一下?
5枝铅笔放在4个盒子里,不管怎么放,总有一个盒子里至少有2枝铅笔。
5枝笔放进4个盒子
把6枝笔放进5个盒子里呢?还用摆吗?
6枝铅笔放在5个盒子里,不管怎么放,总有一个盒子里至少有2枝铅笔。
把7枝笔放进6个盒子里呢?
把8枝笔放进7个盒子里呢?
把9枝笔放进8个盒子里呢?……
铅笔的枝数比盒子数多1,不管怎么放,总有一个盒子里至少有2枝铅笔。
你们的发现和他一样吗
把100枝铅笔放进99个文具盒里会有什么结论?一起说。
你发现什么?
5枝铅笔放进3个盒子呢?你又打算怎样放?
总有一个盒子里至少有2枝还是3枝?为什么?
那么,铅笔的枝数比盒子数量不是只多1呢?还是这种情况吗?
先平均分每个盒子放进1枝笔,余下2只再平均分放进2个不同的盒子里,所以至少2只。
5÷3=1枝……2枝
为什么第二次平均分?
保证“至少”。
只要铅笔数比盒子的数量多,总有一个盒子中至少放进2支铅笔。
“鸽巢原理”(一):把m个物体任意分放进n个鸽巢中(m>n,m和n是非0自然数),那么一定有一个鸽巢中至少放进了2个物体。
你发现什么?
现在我要把把7枝铅笔放进3个盒子。枝数最多的那个盒子至少要放多少枝?
用你喜欢的方法,具体放一放,分一分,画一画,看看会是什么结果。同方同学可以交流。看看至少几枝铅笔会放进同一个盒子?
如果把笔和盒子的数量进一步增加呢?
有更简单的方法吗?需要说明的是数量最多的那个盒子?
(1)7枝笔放进3个盒子,至少几枝放进同一个盒子?
7÷3=2(枝)…1(枝)?
1+1=2(枝)
(2)14枝笔放进4个盒子,至少几枝放进同一个盒子?
14÷4=3(枝)…2(枝)?
3+1=4(枝)
(3)23枝笔放进4个盒子,至少几枝放进同一个盒子?
23÷4=5(枝)…3(枝)?
5+1=6(枝)
对比算式,你发现什么规律?
有没有谁可以用字母来把我们的鸽巢原理表示出来?
要求至少数,都先平均分,再用所得的“商+1”
至少数和余数有没有关系?
与余数无关,不管余多少,都要再平均分,所以就只加1。
物体数÷鸽巢数=商……余数
至少数=商+1
前面我们归纳出了鸽巢原理(一):把m个物体任意分放进n个鸽巢中(m>n,m和n是非0自然数),那么一定有一个鸽巢中至少放进了2个物体。
kn÷n=k……c
(k是正整数,n、c是非0自然数),
至少数=k+1
谁能用自己的话概括我们刚才研究的原理吗?
“鸽巢原理”(二):把多于kn个的物体任意放进n个鸽巢中(k是正整数,n是非0自然数),那么一定有一个鸽巢中至少放进了(k+1)个物体。
谁能用字母把鸽巢原理表示出来?
当c=0时呢?也就是平均分没有余数的时候呢?
至少数该是多少?
课堂小结
通过这节课的学习,你有哪些新的收获呢?
我们学会了简单的鸽巢问题。
可以用动手操作、列举法、画图法来帮助我们分析,也可以用除法的意义来解答。
