第三单元《变量之间的关系》质量检测试卷A(含解析)
文档属性
| 名称 | 第三单元《变量之间的关系》质量检测试卷A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 18:35:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2020-20201年七年级(下)第三章变量间的关系检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
下面每个选项中都给出了某个变化过程中的两个变量
和
,其中
不是
的函数的是
A.
:正方形的面积,:这个正方形的边长
B.
:某班学生的身高,:这个班学生的学号
C.
:圆的面积,:这个圆的直径
D.
:一个正数的平方根,:这个正数
2.
小明和哥哥从家里出发去买书,从家出发走了
分钟到一个离家
米的书店.小明买了书后随即按原路返回;哥哥看了
分钟书后,用
分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系
A.
B.
C.
D.
3.
李师傅到单位附近的加油站加油,如图是其所用的加油机上的数据显示牌,则其中的常量是
A.
金额
B.
数量
C.
单价
D.
金额和数量
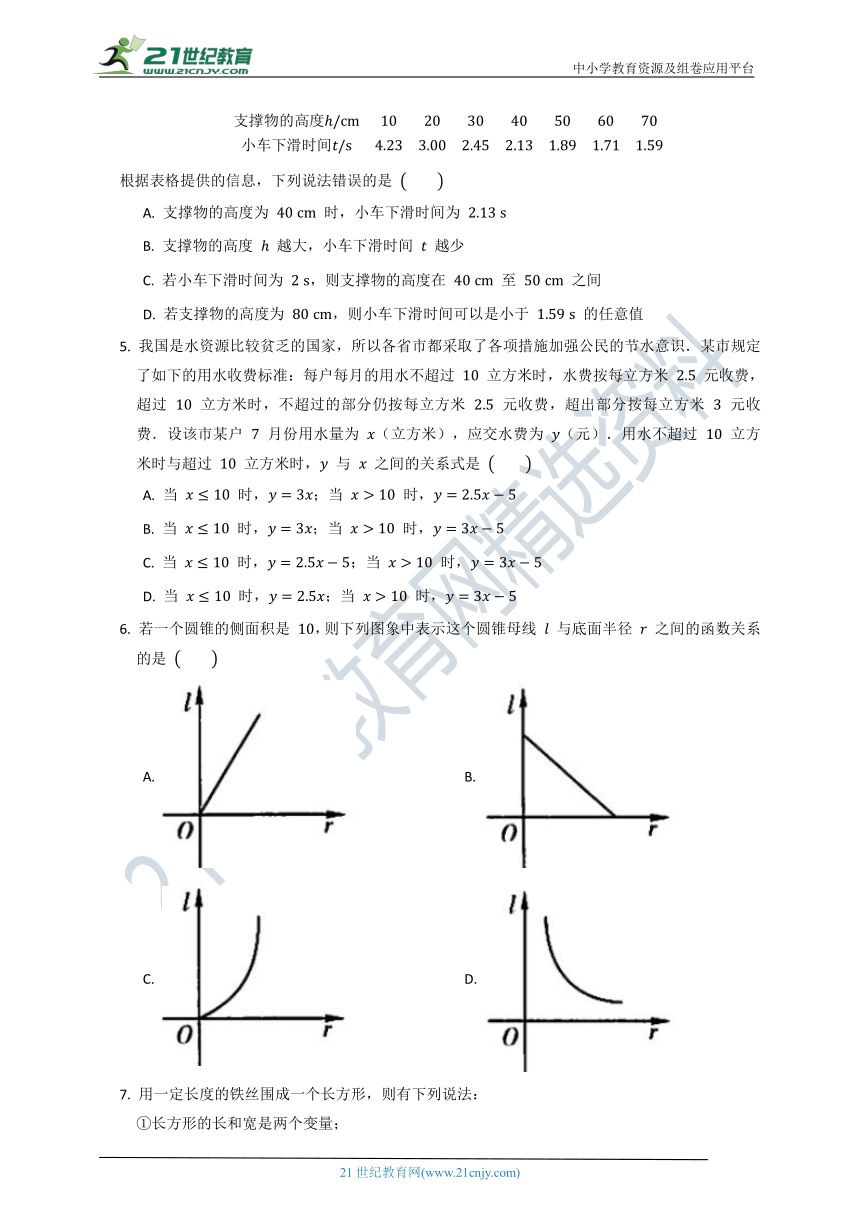
4.
某校七年级数学兴趣小组利用同一块木板测量小车从不同高度斜放的木板上从顶部滑到底部所用的时间,支撑物的高度
与小车下滑时间
之间的关系如下表所示:
根据表格提供的信息,下列说法错误的是
A.
支撑物的高度为
时,小车下滑时间为
B.
支撑物的高度
越大,小车下滑时间
越少
C.
若小车下滑时间为
,则支撑物的高度在
至
之间
D.
若支撑物的高度为
,则小车下滑时间可以是小于
的任意值
5.
我国是水资源比较贫乏的国家,所以各省市都采取了各项措施加强公民的节水意识.某市规定了如下的用水收费标准:每户每月的用水不超过
立方米时,水费按每立方米
元收费,超过
立方米时,不超过的部分仍按每立方米
元收费,超出部分按每立方米
元收费.设该市某户
月份用水量为
(立方米),应交水费为
(元).用水不超过
立方米时与超过
立方米时,
与
之间的关系式是
A.
当
时,;当
时,
B.
当
时,;当
时,
C.
当
时,;当
时,
D.
当
时,;当
时,
6.
若一个圆锥的侧面积是
,则下列图象中表示这个圆锥母线
与底面半径
之间的函数关系的是
A.
B.
C.
D.
7.
用一定长度的铁丝围成一个长方形,则有下列说法:
①长方形的长和宽是两个变量;
②长方形的周长是自变量时,它的宽是因变量;
③长方形的长是自变量时,它的宽是因变量;
④长方形的宽是自变量时,它的长是因变量;
⑤长方形的长是自变量时,它的面积是因变量.
其中正确的说法有
A.
个
B.
个
C.
个
D.
个
8.
笔记本每个
元,买
个笔记本共支出
元,在这个问题中:①
是常量时,
是变量;②
是变量时,
是常量;③
是变量时,
也是变量;④
,
可以都是常量或都是变量.上述判断正确的有
A.
个
B.
个
C.
个
D.
个
9.
某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
下列说法中错误的是
A.
在这个变化过程中,自变量是温度,因变量是声速
B.
温度越高,声速越快
C.
当空气温度为
时,
内声音可以传播
D.
温度每升高
,声速增加
10.
如图①,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度
(单位:)与运动时间
(单位:)的关系的图象如图②,则该小球的运动路程
(单位:)与运动时间
(单位:)之间的关系的图象大致是
A.
B.
C.
D.
11.
一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离
(千米)与行驶时间
(时)的对应关系如图所示,下列叙述正确的是
A.
甲、乙两地相距
千米
B.
快车的速度是
千米/时
C.
慢车的速度是
千米/时
D.
快车到达甲地时,慢车距离乙地
千米
12.
按图
的方式摆放餐桌和椅子,照这样的方式维续摆放,如果摆放的餐桌为
张,摆放的椅子为
把,则
与
之间的关系式为
A.
B.
C.
D.
二、填空题(共6小题;每小题4分,共24分)
13.
河北给武汉运送抗疫物资,某汽车油箱内剩余油量
(升)与汽车行驶路程
(千米)有如下关系:
则该汽车每行驶
千米的耗油量为
?
升.
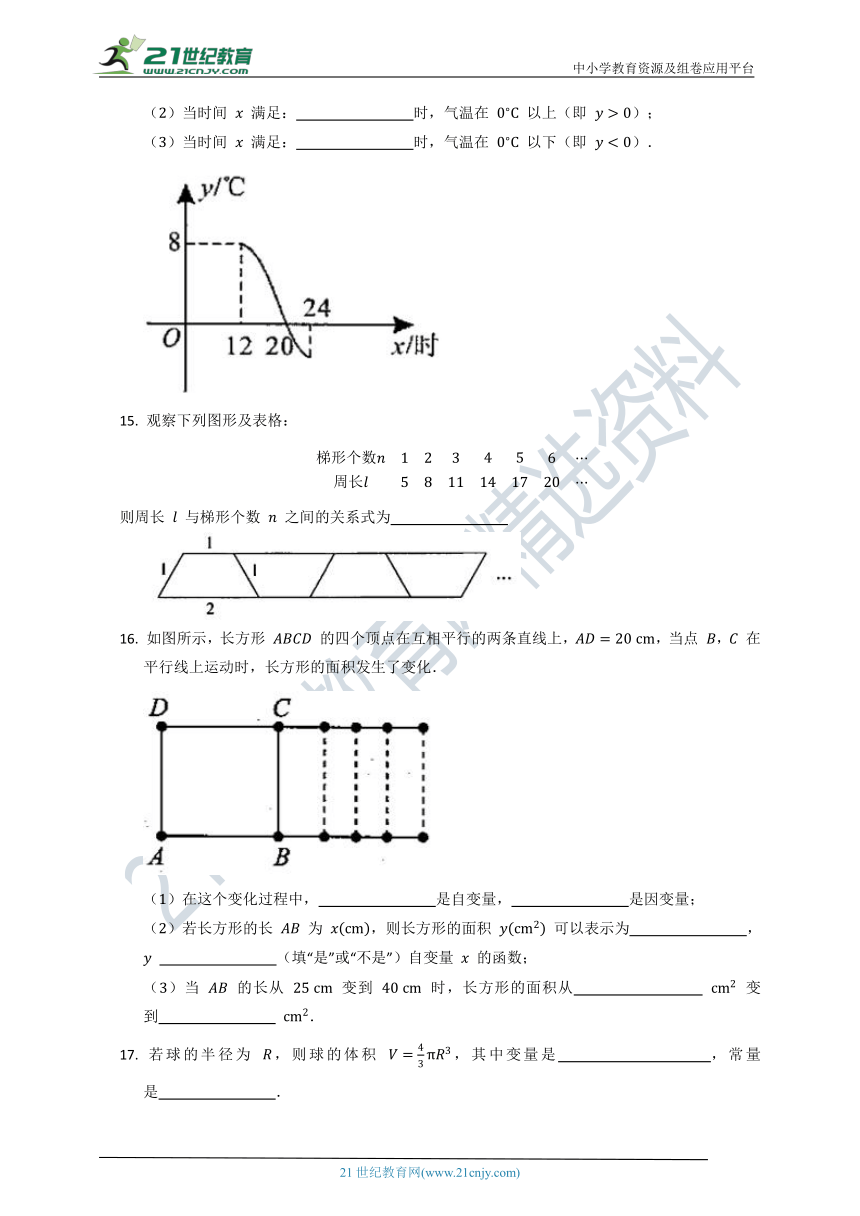
14.
对比学习:如图是某市
时到
时的气温变化图,回答下列问题:
()
?时,气温为
(即
);
()当时间
满足:
?时,气温在
以上(即
);
()当时间
满足:
?时,气温在
以下(即
).
15.
观察下列图形及表格:
则周长
与梯形个数
之间的关系式为
?
16.
如图所示,长方形
的四个顶点在互相平行的两条直线上,,当点
,
在平行线上运动时,长方形的面积发生了变化.
()在这个变化过程中,
?是自变量,
?是因变量;
()若长方形的长
为
,则长方形的面积
可以表示为
?,
?(填“是”或“不是”)自变量
的函数;
()当
的长从
变到
时,长方形的面积从
?
变到
?
.
17.
若球的半径为
,则球的体积
,其中变量是
?,常量是
?.
18.
火车匀速通过隧道时,火车在隧道内的长度
(米)与火车行驶时间
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为
米;
②火车的速度为
米/秒;
③火车整体都在隧道内的时间为
秒;
④隧道长度为
米.
其中正确的结论是
?.(把你认为正确结论的序号都填上)
三、解答题(共7小题;共60分)
19.
(6分)指出下列问题中的变量和常量:
某市的自来水价为
元/
,现要抽取若干户居民调查水费支出情况,记某户月用水量为
,月应交水费为
元.
20.
(10分)某药业集团研究了一种新药,在试验药效时发现,如果儿童按规定剂量服用,那么服用后
小时血液中的含药量最高,接着逐步衰减,每毫升血液中的含药量
(微克)随时间
(时)的变化情况如图所示,当儿童按规定剂量服药后.
(1)血液中的含药量最高是多少微克?
(2)
点表示什么意义?
(3)如果每毫升血液中含药量为
微克以上时治疗疾病有效,那么这个有效时间有多长?
21.
(10分)为了解某品牌轿车以
匀速行驶的耗油情况,进行了实验:该轿车油箱加满后,以
的速度匀速行驶,数据记录如下表:
(1)上表反映了哪两个变量之间的关系?自变量、因变量各是什么?
(2)写出油箱剩余油量
与轿车行驶的路程
之间的函数表达式(不必写出自变量的取值范围);
(3)若小明将油箱加满后,驾驶该轿车以
的速度匀速从A地驶往B地,到达B地时油箱剩余油量为
,求A,B两地之间的距离.
22.
(8分)将一个温度计从一杯热水中取出之后,立即放入一杯凉水中,下面是用表格表示的温度计的读数与时间之间的关系.
(1)上述哪些量在发生变化?自变量和因变量各是什么?
(2)根据表格,大致估计
秒后温度计的读数.
23.
(8分)判断下列变量间是否存在函数关系.
(1)汽车的速度为
千米/时,汽车所行驶的路程(千米)与行驶的时间(时);
(2)一次数学考试中某学生的成绩(分)与该学生的体重(千克);
(3)汽车行驶的速度(千米/时)与驾驶员的身高(厘米);
(4)某班支援灾区的捐款总额(元)与该班学生个人捐款平均数(元).
24.
(10分)如图,
的边
上的高是
,当三角形的顶点
沿边
所在的直线远离点
运动时,三角形的面积发生了变化.
(1)在这个变化过程中,变量有哪些,常量有哪些?
(2)若三角形的边
的长是
,则三角形的面积
可以表示为
?;
(3)当边
的长从
变化到
时,三角形的面积从
?
变化到
?
.
25.
(8分)某商店出售一种商品,质量
与售价
之间的关系如下表:
(1)写出售价
(元)与质量
(千克)的函数关系式;
(2)小张想买此种商品
千克,应付款多少元?
答案
第一部分
1.
D
2.
A
【解析】根据题意可知,从
分钟到
分钟哥哥在书店里看书,离家距离没有变化,是一条平行于横轴的线段故选A.
3.
C
4.
D
【解析】从题表中可以看出,随着支撑物高度的增加,小车下滑的时间在减少,支撑物高度为
时,小车下滑的时间一定比
小,但是它是一个固定值,不可以是小于
的任意值.
5.
D
【解析】当
时,;当
时,.
6.
D
7.
C
【解析】只有②错误,①③④⑤均正确.
8.
B
9.
C
【解析】易知在这个变化过程中,自变量是温度,因变量是声速,
选项A中的说法正确.
根据题表可得,温度越高,声速越快,
选项B中的说法正确.
,
当空气温度为
时,
内声音可以传播
,
选项C中的说法错误.
,,,,,
温度每升高
,声速增加
,
选项D中的说法正确.
10.
C
【解析】由题图可知,C选项中的图象符合要求,故选C.
11.
C
12.
D
【解析】有
张桌子时有
把椅子,
有
张桌子时有
把椅子,,
有
张桌子时有
把椅子,,
多一张餐桌,多放
把椅子,
第
张餐桌共有
.
第二部分
13.
【解析】由题表可得,该汽车每行驶
千米的耗油量为
(升).
14.
,,
15.
【解析】由表格数据找出规律或由图形找出答案.
16.
的长度(或
的长度),长方形
的面积,,是,,
17.
,,,
18.
②③
【解析】火车的长度是
米,故①错误;
如图,
在
段,所用的时间是
秒,路程是
米,则速度是
米/秒,故②正确;
火车整体都在隧道内的时间是
秒,故③正确;
隧道长是
米,故④错误.
故正确的是②③.
第三部分
19.
依题意得:.该函数式中,变量是
、
,常量是
.
20.
(1)
小时血液中的含药量最高,为
微克.
??????(2)
点表示体内的含药量衰减到
微克.
??????(3)
服药后每毫升血液中含药量达到
微克的时间是
时,衰减到
微克的时间是
时,
因此有效时间是
时.
21.
(1)
反映了轿车行驶的路程
和油箱剩余油量
之间的关系,其中轿车行驶的路程
是自变量,油箱剩余油量
是因变量.
??????(2)
.
??????(3)
将
代入
,得
解得
即A,B两地之间的距离为
.
22.
(1)
温度计的读数和时间在发生变化;自变量和因变量分别是时间、温度计的读数.
??????(2)
由表格可看出:随着时间的增加,温度计的读数越来越小,因此
秒时温度计的读数应小于
;
每隔
秒,温度差分别为
,,,,,即温度差越来越小,因此
秒时的温度应大于
,
所以
秒后温度计的读数的范围应为大于
且小于
,
秒后的温度可取这个范围内的任一值,比如可取
等.
23.
(1)
存在.
??????(2)
不存在.
??????(3)
不存在.
??????(4)
存在.
24.
(1)
变量有
的边
的长和面积,常量是高
.
??????(2)
??????(3)
;
25.
(1)
.
??????(2)
当
时,由()得,
.
答:应付
元.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
北师大版2020-20201年七年级(下)第三章变量间的关系检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
下面每个选项中都给出了某个变化过程中的两个变量
和
,其中
不是
的函数的是
A.
:正方形的面积,:这个正方形的边长
B.
:某班学生的身高,:这个班学生的学号
C.
:圆的面积,:这个圆的直径
D.
:一个正数的平方根,:这个正数
2.
小明和哥哥从家里出发去买书,从家出发走了
分钟到一个离家
米的书店.小明买了书后随即按原路返回;哥哥看了
分钟书后,用
分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系
A.
B.
C.
D.
3.
李师傅到单位附近的加油站加油,如图是其所用的加油机上的数据显示牌,则其中的常量是
A.
金额
B.
数量
C.
单价
D.
金额和数量
4.
某校七年级数学兴趣小组利用同一块木板测量小车从不同高度斜放的木板上从顶部滑到底部所用的时间,支撑物的高度
与小车下滑时间
之间的关系如下表所示:
根据表格提供的信息,下列说法错误的是
A.
支撑物的高度为
时,小车下滑时间为
B.
支撑物的高度
越大,小车下滑时间
越少
C.
若小车下滑时间为
,则支撑物的高度在
至
之间
D.
若支撑物的高度为
,则小车下滑时间可以是小于
的任意值
5.
我国是水资源比较贫乏的国家,所以各省市都采取了各项措施加强公民的节水意识.某市规定了如下的用水收费标准:每户每月的用水不超过
立方米时,水费按每立方米
元收费,超过
立方米时,不超过的部分仍按每立方米
元收费,超出部分按每立方米
元收费.设该市某户
月份用水量为
(立方米),应交水费为
(元).用水不超过
立方米时与超过
立方米时,
与
之间的关系式是
A.
当
时,;当
时,
B.
当
时,;当
时,
C.
当
时,;当
时,
D.
当
时,;当
时,
6.
若一个圆锥的侧面积是
,则下列图象中表示这个圆锥母线
与底面半径
之间的函数关系的是
A.
B.
C.
D.
7.
用一定长度的铁丝围成一个长方形,则有下列说法:
①长方形的长和宽是两个变量;
②长方形的周长是自变量时,它的宽是因变量;
③长方形的长是自变量时,它的宽是因变量;
④长方形的宽是自变量时,它的长是因变量;
⑤长方形的长是自变量时,它的面积是因变量.
其中正确的说法有
A.
个
B.
个
C.
个
D.
个
8.
笔记本每个
元,买
个笔记本共支出
元,在这个问题中:①
是常量时,
是变量;②
是变量时,
是常量;③
是变量时,
也是变量;④
,
可以都是常量或都是变量.上述判断正确的有
A.
个
B.
个
C.
个
D.
个
9.
某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
下列说法中错误的是
A.
在这个变化过程中,自变量是温度,因变量是声速
B.
温度越高,声速越快
C.
当空气温度为
时,
内声音可以传播
D.
温度每升高
,声速增加
10.
如图①,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度
(单位:)与运动时间
(单位:)的关系的图象如图②,则该小球的运动路程
(单位:)与运动时间
(单位:)之间的关系的图象大致是
A.
B.
C.
D.
11.
一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离
(千米)与行驶时间
(时)的对应关系如图所示,下列叙述正确的是
A.
甲、乙两地相距
千米
B.
快车的速度是
千米/时
C.
慢车的速度是
千米/时
D.
快车到达甲地时,慢车距离乙地
千米
12.
按图
的方式摆放餐桌和椅子,照这样的方式维续摆放,如果摆放的餐桌为
张,摆放的椅子为
把,则
与
之间的关系式为
A.
B.
C.
D.
二、填空题(共6小题;每小题4分,共24分)
13.
河北给武汉运送抗疫物资,某汽车油箱内剩余油量
(升)与汽车行驶路程
(千米)有如下关系:
则该汽车每行驶
千米的耗油量为
?
升.
14.
对比学习:如图是某市
时到
时的气温变化图,回答下列问题:
()
?时,气温为
(即
);
()当时间
满足:
?时,气温在
以上(即
);
()当时间
满足:
?时,气温在
以下(即
).
15.
观察下列图形及表格:
则周长
与梯形个数
之间的关系式为
?
16.
如图所示,长方形
的四个顶点在互相平行的两条直线上,,当点
,
在平行线上运动时,长方形的面积发生了变化.
()在这个变化过程中,
?是自变量,
?是因变量;
()若长方形的长
为
,则长方形的面积
可以表示为
?,
?(填“是”或“不是”)自变量
的函数;
()当
的长从
变到
时,长方形的面积从
?
变到
?
.
17.
若球的半径为
,则球的体积
,其中变量是
?,常量是
?.
18.
火车匀速通过隧道时,火车在隧道内的长度
(米)与火车行驶时间
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为
米;
②火车的速度为
米/秒;
③火车整体都在隧道内的时间为
秒;
④隧道长度为
米.
其中正确的结论是
?.(把你认为正确结论的序号都填上)
三、解答题(共7小题;共60分)
19.
(6分)指出下列问题中的变量和常量:
某市的自来水价为
元/
,现要抽取若干户居民调查水费支出情况,记某户月用水量为
,月应交水费为
元.
20.
(10分)某药业集团研究了一种新药,在试验药效时发现,如果儿童按规定剂量服用,那么服用后
小时血液中的含药量最高,接着逐步衰减,每毫升血液中的含药量
(微克)随时间
(时)的变化情况如图所示,当儿童按规定剂量服药后.
(1)血液中的含药量最高是多少微克?
(2)
点表示什么意义?
(3)如果每毫升血液中含药量为
微克以上时治疗疾病有效,那么这个有效时间有多长?
21.
(10分)为了解某品牌轿车以
匀速行驶的耗油情况,进行了实验:该轿车油箱加满后,以
的速度匀速行驶,数据记录如下表:
(1)上表反映了哪两个变量之间的关系?自变量、因变量各是什么?
(2)写出油箱剩余油量
与轿车行驶的路程
之间的函数表达式(不必写出自变量的取值范围);
(3)若小明将油箱加满后,驾驶该轿车以
的速度匀速从A地驶往B地,到达B地时油箱剩余油量为
,求A,B两地之间的距离.
22.
(8分)将一个温度计从一杯热水中取出之后,立即放入一杯凉水中,下面是用表格表示的温度计的读数与时间之间的关系.
(1)上述哪些量在发生变化?自变量和因变量各是什么?
(2)根据表格,大致估计
秒后温度计的读数.
23.
(8分)判断下列变量间是否存在函数关系.
(1)汽车的速度为
千米/时,汽车所行驶的路程(千米)与行驶的时间(时);
(2)一次数学考试中某学生的成绩(分)与该学生的体重(千克);
(3)汽车行驶的速度(千米/时)与驾驶员的身高(厘米);
(4)某班支援灾区的捐款总额(元)与该班学生个人捐款平均数(元).
24.
(10分)如图,
的边
上的高是
,当三角形的顶点
沿边
所在的直线远离点
运动时,三角形的面积发生了变化.
(1)在这个变化过程中,变量有哪些,常量有哪些?
(2)若三角形的边
的长是
,则三角形的面积
可以表示为
?;
(3)当边
的长从
变化到
时,三角形的面积从
?
变化到
?
.
25.
(8分)某商店出售一种商品,质量
与售价
之间的关系如下表:
(1)写出售价
(元)与质量
(千克)的函数关系式;
(2)小张想买此种商品
千克,应付款多少元?
答案
第一部分
1.
D
2.
A
【解析】根据题意可知,从
分钟到
分钟哥哥在书店里看书,离家距离没有变化,是一条平行于横轴的线段故选A.
3.
C
4.
D
【解析】从题表中可以看出,随着支撑物高度的增加,小车下滑的时间在减少,支撑物高度为
时,小车下滑的时间一定比
小,但是它是一个固定值,不可以是小于
的任意值.
5.
D
【解析】当
时,;当
时,.
6.
D
7.
C
【解析】只有②错误,①③④⑤均正确.
8.
B
9.
C
【解析】易知在这个变化过程中,自变量是温度,因变量是声速,
选项A中的说法正确.
根据题表可得,温度越高,声速越快,
选项B中的说法正确.
,
当空气温度为
时,
内声音可以传播
,
选项C中的说法错误.
,,,,,
温度每升高
,声速增加
,
选项D中的说法正确.
10.
C
【解析】由题图可知,C选项中的图象符合要求,故选C.
11.
C
12.
D
【解析】有
张桌子时有
把椅子,
有
张桌子时有
把椅子,,
有
张桌子时有
把椅子,,
多一张餐桌,多放
把椅子,
第
张餐桌共有
.
第二部分
13.
【解析】由题表可得,该汽车每行驶
千米的耗油量为
(升).
14.
,,
15.
【解析】由表格数据找出规律或由图形找出答案.
16.
的长度(或
的长度),长方形
的面积,,是,,
17.
,,,
18.
②③
【解析】火车的长度是
米,故①错误;
如图,
在
段,所用的时间是
秒,路程是
米,则速度是
米/秒,故②正确;
火车整体都在隧道内的时间是
秒,故③正确;
隧道长是
米,故④错误.
故正确的是②③.
第三部分
19.
依题意得:.该函数式中,变量是
、
,常量是
.
20.
(1)
小时血液中的含药量最高,为
微克.
??????(2)
点表示体内的含药量衰减到
微克.
??????(3)
服药后每毫升血液中含药量达到
微克的时间是
时,衰减到
微克的时间是
时,
因此有效时间是
时.
21.
(1)
反映了轿车行驶的路程
和油箱剩余油量
之间的关系,其中轿车行驶的路程
是自变量,油箱剩余油量
是因变量.
??????(2)
.
??????(3)
将
代入
,得
解得
即A,B两地之间的距离为
.
22.
(1)
温度计的读数和时间在发生变化;自变量和因变量分别是时间、温度计的读数.
??????(2)
由表格可看出:随着时间的增加,温度计的读数越来越小,因此
秒时温度计的读数应小于
;
每隔
秒,温度差分别为
,,,,,即温度差越来越小,因此
秒时的温度应大于
,
所以
秒后温度计的读数的范围应为大于
且小于
,
秒后的温度可取这个范围内的任一值,比如可取
等.
23.
(1)
存在.
??????(2)
不存在.
??????(3)
不存在.
??????(4)
存在.
24.
(1)
变量有
的边
的长和面积,常量是高
.
??????(2)
??????(3)
;
25.
(1)
.
??????(2)
当
时,由()得,
.
答:应付
元.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
