2020-2021学年北师大版八年级数学下册第二章2.5一元一次不等式和一次函数同步考点练(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册第二章2.5一元一次不等式和一次函数同步考点练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 912.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-10 22:10:21 | ||
图片预览


文档简介
2020-2021学年北师大版八年级数学下册第二章2.5一元一次不等式和一次函数同步考点练
一、单选题
1.下列关于一次函数y=﹣2x+2的图象的说法中,错误的是(
)
A.函数图象经过第一、二、四象限
B.函数图象与x轴的交点坐标为(2,0)
C.当x>0时,y<2
D.y的值随着x值的增大而减小
2.已知直线与直线的交点坐标为,则关于的不等式的解集为(
)
A.
B.
C.
D.
3.如图,函数y=ax+4和y=2x的图象相交于点A(1,m),则不等式ax+4>2x的解集为(
)
A.x>1
B.x<1
C.x>2
D.x<2
4.一次函数中与的部分对应值如下表,则不等式的解是(
)
x
-2
-1
0
1
y
5
3
1
-1
A.
B.
C.
D.
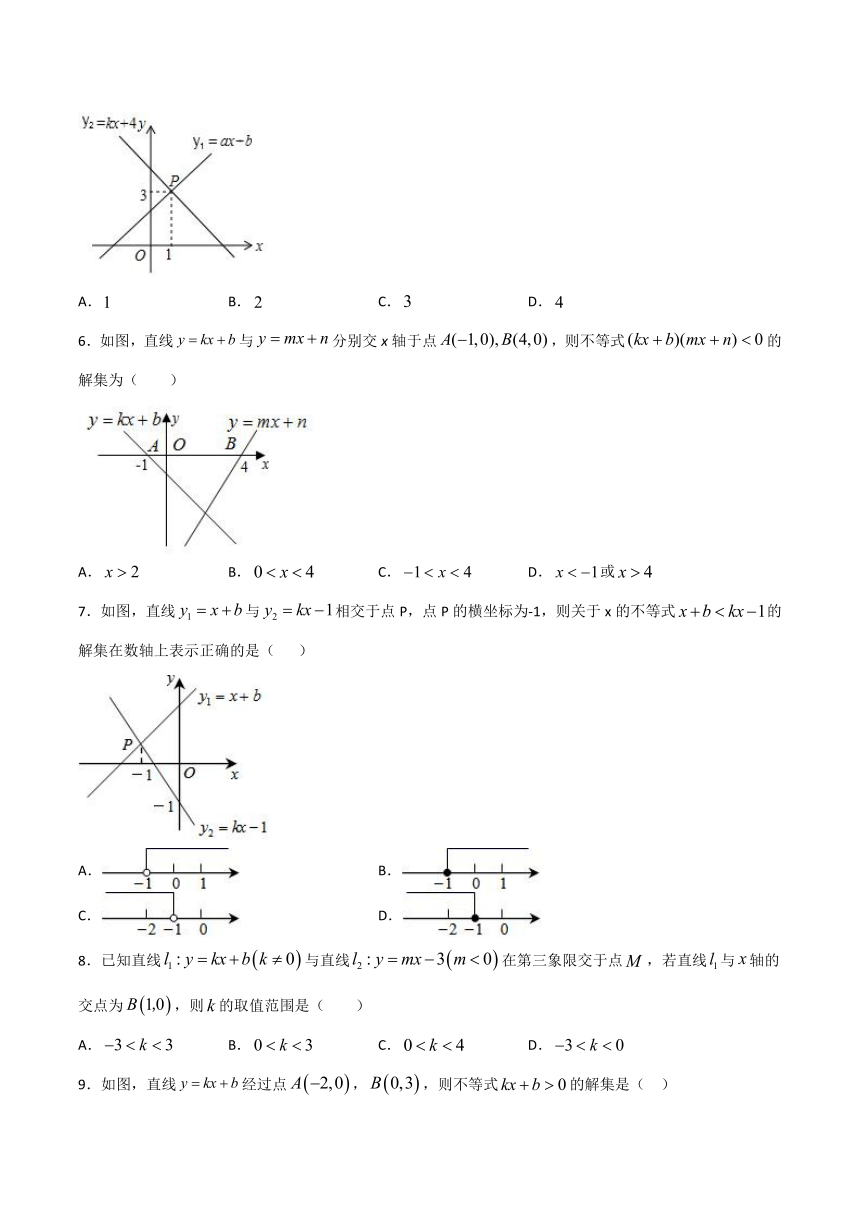
5.如图,一次函数与一次函数的图象交点,则下列说法正确的个数是(
)
①是方程的一个解;
②方程组的解是;③不等式的解集是;
④不等式的解集是.
A.
B.
C.
D.
6.如图,直线与分别交x轴于点,则不等式的解集为(
)
A.
B.
C.
D.或
7.如图,直线与相交于点P,点P的横坐标为-1,则关于x的不等式的解集在数轴上表示正确的是(
)
A.
B.
C.
D.
8.已知直线与直线在第三象限交于点,若直线与轴的交点为,则的取值范围是(
)
A.
B.
C.
D.
9.如图,直线经过点,,则不等式的解集是(
)
A.
B.
C.
D.
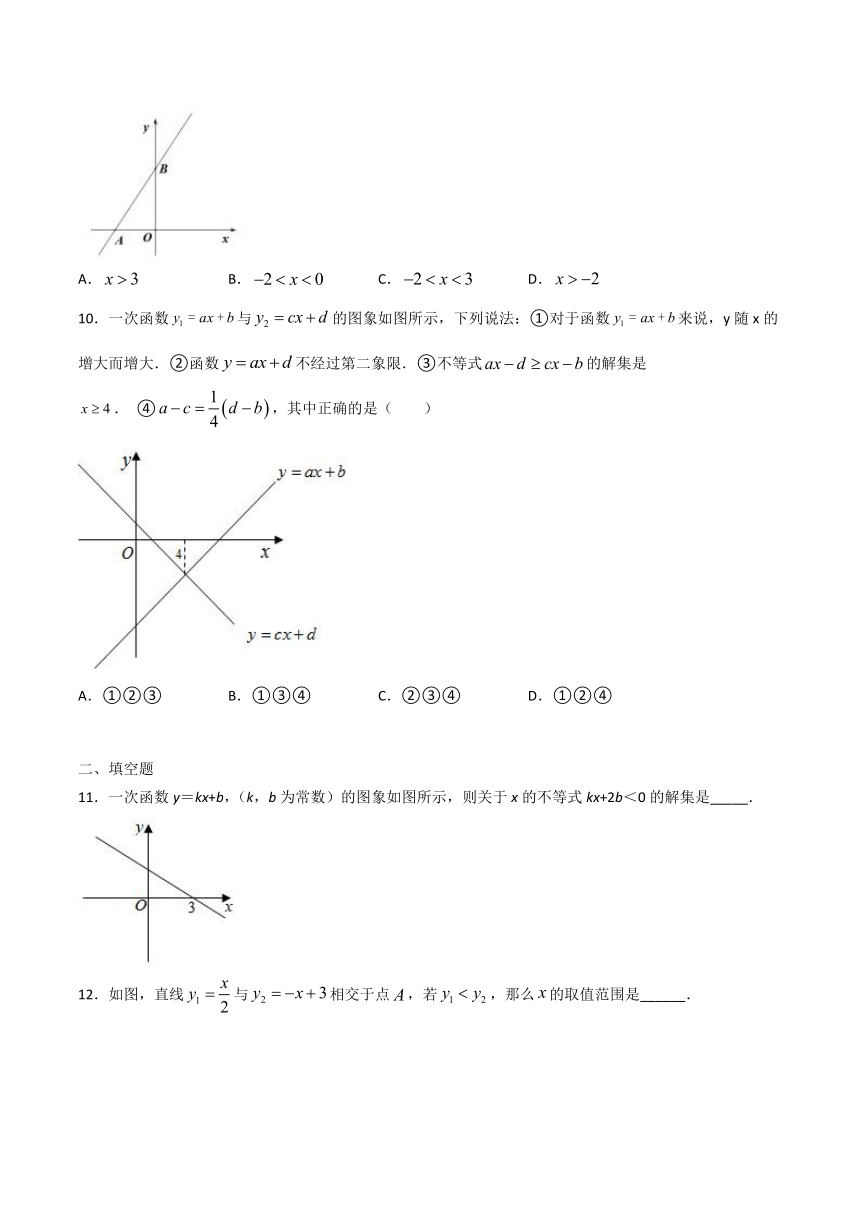
10.一次函数与的图象如图所示,下列说法:①对于函数来说,y随x的增大而增大.②函数不经过第二象限.③不等式的解集是.
④,其中正确的是(
)
A.①②③
B.①③④
C.②③④
D.①②④
二、填空题
11.一次函数y=kx+b,(k,b为常数)的图象如图所示,则关于x的不等式kx+2b<0的解集是_____.
12.如图,直线与相交于点,若,那么的取值范围是______.
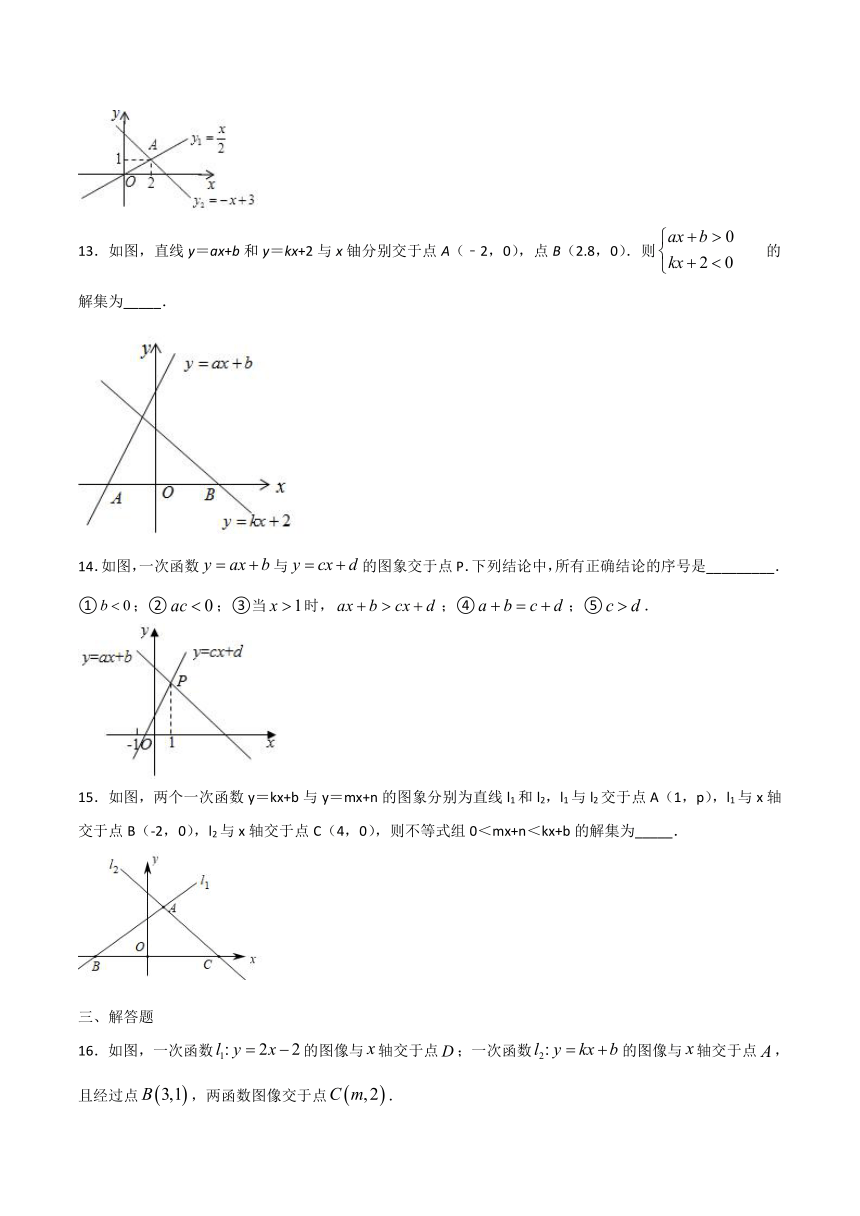
13.如图,直线y=ax+b和y=kx+2与x铀分别交于点A(﹣2,0),点B(2.8,0).则的解集为_____.
14.如图,一次函数与的图象交于点P.下列结论中,所有正确结论的序号是_________.
①;②;③当时,;④;⑤.
15.如图,两个一次函数y=kx+b与y=mx+n的图象分别为直线l1和l2,l1与l2交于点A(1,p),l1与x轴交于点B(-2,0),l2与x轴交于点C(4,0),则不等式组0<mx+n<kx+b的解集为_____.
三、解答题
16.如图,一次函数的图像与轴交于点;一次函数的图像与轴交于点,且经过点,两函数图像交于点.
(1)求,,的值;
(2)根据图象,直接写出的解集.
17.在平面直角坐标系中,直线:与轴交于点,与直线:交于点.
(1)分别求出直线和直线的表达式;
(2)直接写出不等式解集.
18.如图,在平面直角坐标系中,直线与x轴交于点A,直线与x轴交于点B,且与直线交于点.
(1)求m和b的值;
(2)求的面积;
(3)若将直线向下平移个单位长度后,所得到的直线与直线的交点在第一象限,直接写出t的取值范围.
19.如图,在平面直角坐标系中,一次函数y=﹣x+n图象与正比例函数y=2x的图象交于点A(m,4).
(1)求m,n的值;
(2)设一次函数y=﹣x+n的图象与x轴交于点B,与y轴交于点C,求点B,点C的坐标;
(3)直接写出使函数y=﹣x+n的值小于函数y=2x的值的自变量x的取值范围.
(4)在x轴上是否存在点P使△PAB为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
20.某校组织元旦汇演,准备购进,两种文具共40件作为奖品,设购进种文具件,总费用为元.,文具的费用与的函数关系如下表.
(件)
8
9
12
种文具费用(元)
120
135
______
种文具费用(元)
640
______
560
(1)将表格补充完整.
(2)求关于的函数表达式.
(3)当种文具的费用不大于种文具的费用时,求总费用的最小值.
21.小南根据学习函数的经验,对函数的图象与性质进行了探究.下表是小南探究过程中的部分信息:
…
-4
-3
-2
-1
0
1
2
3
4
…
…
3
2
1
0
-1
-2
-2
-1
…
请按要求完成下列各小题:
(1)该函数的解析式为
,自变量
x
的取值范围为
;
(2)的值为
;点
该函数图象上;(填“在”或“不在”)
(3)在如图所示的平面直角坐标系中,描全上表中以各对对应值为
坐标的点,并画出该函数的图象;
(4)结合函数的图象,解决问题:
①写出该函数的一条性质:
;
②如图,在同一坐标系中是一次函数的图象,根据象回答,当时,自变量
x
的取值范围为
.
参考答案
1.B
解:A、∵k=﹣2<0,b=2>0,∴函数图象经过第一、二、四象限,说法正确;
B、∵y=0时,x=1,∴函数图象与x轴的交点坐标为(1,0),说法错误;
C、当x=0时,y=2,由k=﹣2<0,∴y的值随着x值的增大而减小,∴当x>0时,y<2,说法正确;
D、∵k=﹣2<0,∴y的值随着x值的增大而减小,说法正确;
2.A
解:∵k<0,
∴中随x的增大而减小,
∵m>0,
∴中随x的增大而增大,
∵两直线交点坐标为,
∴当x>时,的图像在上方,
∴不等式的解集为为x>,
3.B
解:∵函数y=2x的图象经过点A(1,m),
∴m=2,
∴点A(1,2),
所以,当x<1时,2x<ax+4,
即不等式2x<ax+4的解集为x<1.
故选:B.
4.D
把x=0,y=1;x=1,y=?1分别代入y=kx+b中,得:
解得:
所以一次函数的解析式为:y=?2x+1
解方程:?2x+1=0,得x=0.5
所以?2x+1>0的解为:x<0.5
故选:D
5.C
解:①如图所示,一次函数与一次函数的图象交于点,则点位于直线上,所以是方程的一个解,故①说法正确.
②如图所示,一次函数与一次函数的图象交于点,则方程组的解是,故②说法错误.
③如图所示,一次函数与一次函数的图象交于点,则不等式的解集是,故③说法正确.
④如图所示,一次函数与一次函数的图象交于点,且直线与轴的交点是,则不等式的解集是,故④说法正确.
综上所述,说法正确的个数是3,
故选:.
6.D
解:
∵直线y=kx+b与直线y=mx+n分别交x轴于点A(?1,0),B(4,0),
∴或时,且或者且,
∴不等式的解集为:或.
7.C
由图像可知当x<-1时,,
∴可在数轴上表示为:
故选C.
8.B
解:∵直线与x轴的交点为B(1,0),
∴k+b=0,则b=?k,
∴y=kx?k,
直线与y轴的交点坐标为(0,?3),
则与y轴交点(0,?k)在原点和点(0,?3)之间,
即:?3<?k<0,
解得:0<k<3,
9.D
解:∵直线y=kx+b交x轴于A(-2,0),
结合函数图形可知不等式kx+b>0解集对应直线在x轴上方部分图象上点的横坐标的集合;
∴不等式kx+b>0的解集是x>-2,
10.B
解:由图象可得:对于函数来说,从左到右,图象上升,y随x的增大而增大,故①正确;
由图象可知,a>0,d>0,所以函数的图象经过第一,二,三象限,即不经过第四象限,故②错误,
由图象可得当时,一次函数图象在的图象上方,
不等式的解集是,
移项可得,,解集是,故③正确;
∵一次函数与的图象的交点的横坐标为4,
∴
∴,
∴,故④正确,
11.x>6
解:把(3,0)代入y=kx+b得,3k+b=0,
∴b=﹣3k,
∵kx+2b<0,
∴kx<6k,
由图象可知k<0,
∴x>6,
故答案为x>6.
12.x<2
解:从图象上得出,当y1<y2时,x<2.
故答案为:x<2.
13.x>2.8
解:由图象得直线y=ax+b中y随x的增大而增大,与x铀交于点A(﹣2,0),
∴不等式解集为x>-2,
由图象得直线y=kx+2中y随x的增大而减小,与x铀交于点B(2.8,0),
∴不等式解集为x>2.8,
∴的解集为x>2.8.
故答案为:x>2.8
14.②④⑤
解:①由图象可得:一次函数y=ax+b图象经过一、二、四象限,
∴a<0,b>0,故①错误;
②由图象可得:一次函数y=cx+d图象经过一、二、三象限,
∴c>0,d>0,
∴ac<0,故②正确;
③由图象可得:当x>1时,一次函数y=ax+b图象在y=cx+d的图象下方,
∴ax+b<cx+d,故③错误;
④∵一次函数y=ax+b与y=cx+d的图象的交点P的横坐标为1,
∴a+b=c+d,故④正确;
⑤∵一次函数y=cx+d图象与x轴的交点坐标为(,0),且>-1,c>0,
∴c>d.故⑤正确.
故答案为:②④⑤.
15.1<x<4
解:
不等式0<mx+n,
上的点在轴的上方,
<
mx+n<kx+b,
上的点在的上方,
,
>
不等式组0<mx+n<kx+b的解集为1<<4,
故答案为:1<<4,
16.解:(1)点在直线上,
,
解得;
点、在直线上,
,
解得:;
(2)由图象可得,不等式组的解集为.
17.
解:(1)把点,代入直线:,
得,
解得,
直线的表达式为;
将代入直线:,
得,,
解得,
直线的表达式为;
(2)不等式,
根据图像直线:在直线的下方,
在交点A右侧部分满足条件,
所以.
18.
解:(1)把代入,得
,
把代入,得
,
∴b=4;
(2)当时,
解得x=2,
∴A(2,0);
当时,
解得x=-2,
∴B(-2,0);
∴AB=4,
∴的面积=;
(3)设平移后的解析式为,
当x=0时,,
∴D(0,),
把D(0,)代入,得
,
∴t=;
把A(2,0)代入,得
,
∴t=8;
∴t的取值范围19.
解:(1)正比例函数y=2x的图象过点A(m,4).
∴4=2m,
∴m=2.
又∵一次函数y=﹣x+n的图象过点A(2,4).
∴4=﹣2+n,
∴n=6.
(2)一次函数y=﹣x+n的图象与x轴交于点B,
∴令y=0,则0=﹣x+6
∴x=6,
∴点B坐标为(6,0),
令x=0,则y=6,
∴点C坐标为(0,6);
(3)由图象可知,在交点A的右侧,函数y=﹣x+n的值小于函数y=2x的值,此时自变量的取值范围是:x>2;
(4)∵点A(2,4),点B坐标为(6,0),
∴AB=,
当AB=BP=4时,则点P(6+4,0)或(6﹣4,0);
当AB=AP时,如图,过点A作AE⊥BO于E,则点E(2,0),
∵AB=AP,AE⊥BO,
∴PE=BE=4,
∴点P(﹣2,0);
当PA=PB时,
∴∠PBA=∠PAB=45°,
∴∠APB=90°,
∴点P(2,0),
20.
(1)
(件)
8
9
12
种文具费用(元)
120
135
180
种文具费用(元)
640
620
560
(2)由题意,种文具15元/件,种文具20元/件,
设购进种文具件,则种文具数量为件,
∴;
(3)∵,
∴,
∵,,
∴随着的增大而减小,
∴当时,,
答:总费用最少为690元.
21.解:(1)把x=-4,y=3;x=-3,y=2代入,
得,
解得,,
∴该函数的解析式为;自变量
x
的取值范围为全体实数;
故答案是:;全体实数;
(2)在中,当x=2时,,
∴n=-3.
当x=时,,
∴点不在函数的图象上;
故答案为:-3;不在;
(3)该函数的图象如图:
(4)①从图象可以看出,该函数有最小值为-3;
故答案为:函数有最小值为-3;
②从图象可以看出,当时的图象位于的图象的下方,
∴当时,自变量
x
的取值范围为.
故答案为:.
试卷第1页,总3页
一、单选题
1.下列关于一次函数y=﹣2x+2的图象的说法中,错误的是(
)
A.函数图象经过第一、二、四象限
B.函数图象与x轴的交点坐标为(2,0)
C.当x>0时,y<2
D.y的值随着x值的增大而减小
2.已知直线与直线的交点坐标为,则关于的不等式的解集为(
)
A.
B.
C.
D.
3.如图,函数y=ax+4和y=2x的图象相交于点A(1,m),则不等式ax+4>2x的解集为(
)
A.x>1
B.x<1
C.x>2
D.x<2
4.一次函数中与的部分对应值如下表,则不等式的解是(
)
x
-2
-1
0
1
y
5
3
1
-1
A.
B.
C.
D.
5.如图,一次函数与一次函数的图象交点,则下列说法正确的个数是(
)
①是方程的一个解;
②方程组的解是;③不等式的解集是;
④不等式的解集是.
A.
B.
C.
D.
6.如图,直线与分别交x轴于点,则不等式的解集为(
)
A.
B.
C.
D.或
7.如图,直线与相交于点P,点P的横坐标为-1,则关于x的不等式的解集在数轴上表示正确的是(
)
A.
B.
C.
D.
8.已知直线与直线在第三象限交于点,若直线与轴的交点为,则的取值范围是(
)
A.
B.
C.
D.
9.如图,直线经过点,,则不等式的解集是(
)
A.
B.
C.
D.
10.一次函数与的图象如图所示,下列说法:①对于函数来说,y随x的增大而增大.②函数不经过第二象限.③不等式的解集是.
④,其中正确的是(
)
A.①②③
B.①③④
C.②③④
D.①②④
二、填空题
11.一次函数y=kx+b,(k,b为常数)的图象如图所示,则关于x的不等式kx+2b<0的解集是_____.
12.如图,直线与相交于点,若,那么的取值范围是______.
13.如图,直线y=ax+b和y=kx+2与x铀分别交于点A(﹣2,0),点B(2.8,0).则的解集为_____.
14.如图,一次函数与的图象交于点P.下列结论中,所有正确结论的序号是_________.
①;②;③当时,;④;⑤.
15.如图,两个一次函数y=kx+b与y=mx+n的图象分别为直线l1和l2,l1与l2交于点A(1,p),l1与x轴交于点B(-2,0),l2与x轴交于点C(4,0),则不等式组0<mx+n<kx+b的解集为_____.
三、解答题
16.如图,一次函数的图像与轴交于点;一次函数的图像与轴交于点,且经过点,两函数图像交于点.
(1)求,,的值;
(2)根据图象,直接写出的解集.
17.在平面直角坐标系中,直线:与轴交于点,与直线:交于点.
(1)分别求出直线和直线的表达式;
(2)直接写出不等式解集.
18.如图,在平面直角坐标系中,直线与x轴交于点A,直线与x轴交于点B,且与直线交于点.
(1)求m和b的值;
(2)求的面积;
(3)若将直线向下平移个单位长度后,所得到的直线与直线的交点在第一象限,直接写出t的取值范围.
19.如图,在平面直角坐标系中,一次函数y=﹣x+n图象与正比例函数y=2x的图象交于点A(m,4).
(1)求m,n的值;
(2)设一次函数y=﹣x+n的图象与x轴交于点B,与y轴交于点C,求点B,点C的坐标;
(3)直接写出使函数y=﹣x+n的值小于函数y=2x的值的自变量x的取值范围.
(4)在x轴上是否存在点P使△PAB为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
20.某校组织元旦汇演,准备购进,两种文具共40件作为奖品,设购进种文具件,总费用为元.,文具的费用与的函数关系如下表.
(件)
8
9
12
种文具费用(元)
120
135
______
种文具费用(元)
640
______
560
(1)将表格补充完整.
(2)求关于的函数表达式.
(3)当种文具的费用不大于种文具的费用时,求总费用的最小值.
21.小南根据学习函数的经验,对函数的图象与性质进行了探究.下表是小南探究过程中的部分信息:
…
-4
-3
-2
-1
0
1
2
3
4
…
…
3
2
1
0
-1
-2
-2
-1
…
请按要求完成下列各小题:
(1)该函数的解析式为
,自变量
x
的取值范围为
;
(2)的值为
;点
该函数图象上;(填“在”或“不在”)
(3)在如图所示的平面直角坐标系中,描全上表中以各对对应值为
坐标的点,并画出该函数的图象;
(4)结合函数的图象,解决问题:
①写出该函数的一条性质:
;
②如图,在同一坐标系中是一次函数的图象,根据象回答,当时,自变量
x
的取值范围为
.
参考答案
1.B
解:A、∵k=﹣2<0,b=2>0,∴函数图象经过第一、二、四象限,说法正确;
B、∵y=0时,x=1,∴函数图象与x轴的交点坐标为(1,0),说法错误;
C、当x=0时,y=2,由k=﹣2<0,∴y的值随着x值的增大而减小,∴当x>0时,y<2,说法正确;
D、∵k=﹣2<0,∴y的值随着x值的增大而减小,说法正确;
2.A
解:∵k<0,
∴中随x的增大而减小,
∵m>0,
∴中随x的增大而增大,
∵两直线交点坐标为,
∴当x>时,的图像在上方,
∴不等式的解集为为x>,
3.B
解:∵函数y=2x的图象经过点A(1,m),
∴m=2,
∴点A(1,2),
所以,当x<1时,2x<ax+4,
即不等式2x<ax+4的解集为x<1.
故选:B.
4.D
把x=0,y=1;x=1,y=?1分别代入y=kx+b中,得:
解得:
所以一次函数的解析式为:y=?2x+1
解方程:?2x+1=0,得x=0.5
所以?2x+1>0的解为:x<0.5
故选:D
5.C
解:①如图所示,一次函数与一次函数的图象交于点,则点位于直线上,所以是方程的一个解,故①说法正确.
②如图所示,一次函数与一次函数的图象交于点,则方程组的解是,故②说法错误.
③如图所示,一次函数与一次函数的图象交于点,则不等式的解集是,故③说法正确.
④如图所示,一次函数与一次函数的图象交于点,且直线与轴的交点是,则不等式的解集是,故④说法正确.
综上所述,说法正确的个数是3,
故选:.
6.D
解:
∵直线y=kx+b与直线y=mx+n分别交x轴于点A(?1,0),B(4,0),
∴或时,且或者且,
∴不等式的解集为:或.
7.C
由图像可知当x<-1时,,
∴可在数轴上表示为:
故选C.
8.B
解:∵直线与x轴的交点为B(1,0),
∴k+b=0,则b=?k,
∴y=kx?k,
直线与y轴的交点坐标为(0,?3),
则与y轴交点(0,?k)在原点和点(0,?3)之间,
即:?3<?k<0,
解得:0<k<3,
9.D
解:∵直线y=kx+b交x轴于A(-2,0),
结合函数图形可知不等式kx+b>0解集对应直线在x轴上方部分图象上点的横坐标的集合;
∴不等式kx+b>0的解集是x>-2,
10.B
解:由图象可得:对于函数来说,从左到右,图象上升,y随x的增大而增大,故①正确;
由图象可知,a>0,d>0,所以函数的图象经过第一,二,三象限,即不经过第四象限,故②错误,
由图象可得当时,一次函数图象在的图象上方,
不等式的解集是,
移项可得,,解集是,故③正确;
∵一次函数与的图象的交点的横坐标为4,
∴
∴,
∴,故④正确,
11.x>6
解:把(3,0)代入y=kx+b得,3k+b=0,
∴b=﹣3k,
∵kx+2b<0,
∴kx<6k,
由图象可知k<0,
∴x>6,
故答案为x>6.
12.x<2
解:从图象上得出,当y1<y2时,x<2.
故答案为:x<2.
13.x>2.8
解:由图象得直线y=ax+b中y随x的增大而增大,与x铀交于点A(﹣2,0),
∴不等式解集为x>-2,
由图象得直线y=kx+2中y随x的增大而减小,与x铀交于点B(2.8,0),
∴不等式解集为x>2.8,
∴的解集为x>2.8.
故答案为:x>2.8
14.②④⑤
解:①由图象可得:一次函数y=ax+b图象经过一、二、四象限,
∴a<0,b>0,故①错误;
②由图象可得:一次函数y=cx+d图象经过一、二、三象限,
∴c>0,d>0,
∴ac<0,故②正确;
③由图象可得:当x>1时,一次函数y=ax+b图象在y=cx+d的图象下方,
∴ax+b<cx+d,故③错误;
④∵一次函数y=ax+b与y=cx+d的图象的交点P的横坐标为1,
∴a+b=c+d,故④正确;
⑤∵一次函数y=cx+d图象与x轴的交点坐标为(,0),且>-1,c>0,
∴c>d.故⑤正确.
故答案为:②④⑤.
15.1<x<4
解:
不等式0<mx+n,
上的点在轴的上方,
<
mx+n<kx+b,
上的点在的上方,
,
>
不等式组0<mx+n<kx+b的解集为1<<4,
故答案为:1<<4,
16.解:(1)点在直线上,
,
解得;
点、在直线上,
,
解得:;
(2)由图象可得,不等式组的解集为.
17.
解:(1)把点,代入直线:,
得,
解得,
直线的表达式为;
将代入直线:,
得,,
解得,
直线的表达式为;
(2)不等式,
根据图像直线:在直线的下方,
在交点A右侧部分满足条件,
所以.
18.
解:(1)把代入,得
,
把代入,得
,
∴b=4;
(2)当时,
解得x=2,
∴A(2,0);
当时,
解得x=-2,
∴B(-2,0);
∴AB=4,
∴的面积=;
(3)设平移后的解析式为,
当x=0时,,
∴D(0,),
把D(0,)代入,得
,
∴t=;
把A(2,0)代入,得
,
∴t=8;
∴t的取值范围
解:(1)正比例函数y=2x的图象过点A(m,4).
∴4=2m,
∴m=2.
又∵一次函数y=﹣x+n的图象过点A(2,4).
∴4=﹣2+n,
∴n=6.
(2)一次函数y=﹣x+n的图象与x轴交于点B,
∴令y=0,则0=﹣x+6
∴x=6,
∴点B坐标为(6,0),
令x=0,则y=6,
∴点C坐标为(0,6);
(3)由图象可知,在交点A的右侧,函数y=﹣x+n的值小于函数y=2x的值,此时自变量的取值范围是:x>2;
(4)∵点A(2,4),点B坐标为(6,0),
∴AB=,
当AB=BP=4时,则点P(6+4,0)或(6﹣4,0);
当AB=AP时,如图,过点A作AE⊥BO于E,则点E(2,0),
∵AB=AP,AE⊥BO,
∴PE=BE=4,
∴点P(﹣2,0);
当PA=PB时,
∴∠PBA=∠PAB=45°,
∴∠APB=90°,
∴点P(2,0),
20.
(1)
(件)
8
9
12
种文具费用(元)
120
135
180
种文具费用(元)
640
620
560
(2)由题意,种文具15元/件,种文具20元/件,
设购进种文具件,则种文具数量为件,
∴;
(3)∵,
∴,
∵,,
∴随着的增大而减小,
∴当时,,
答:总费用最少为690元.
21.解:(1)把x=-4,y=3;x=-3,y=2代入,
得,
解得,,
∴该函数的解析式为;自变量
x
的取值范围为全体实数;
故答案是:;全体实数;
(2)在中,当x=2时,,
∴n=-3.
当x=时,,
∴点不在函数的图象上;
故答案为:-3;不在;
(3)该函数的图象如图:
(4)①从图象可以看出,该函数有最小值为-3;
故答案为:函数有最小值为-3;
②从图象可以看出,当时的图象位于的图象的下方,
∴当时,自变量
x
的取值范围为.
故答案为:.
试卷第1页,总3页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
