2020-2021学年北师大版七年级数学下册第四章《三角形》章末同步单元练习题(word版,含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第四章《三角形》章末同步单元练习题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 171.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 00:00:00 | ||
图片预览




文档简介
2020-2021学年北师大版七年级数学下册第四章
三角形
章末同步单元练习题
A组(基础题)
一、填空题
1.如图,在△ABC中,BD=DE=EC,则AD,AE分别是___________的中线.
2.(1)三角形的三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是_________三角形.
(2)已知AD为△ABC的中线,AB=5
cm,且△ACD的周长比△ABD的周长少2
cm,则AC=_________.
3.如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=_________.
4.(1)等腰三角形有两边长分别为5和10,则它的周长为_________.
(2)(2020·成都青羊区期末)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD交AD的延长线于点E.若∠DBE=25°,则∠CAB=_________.
二、选择题
5.已知直线a∥b,Rt△DCB按如图所示的方式放置,点C在直线b上,∠DCB=90°,若∠B=20°,则∠1+∠2的度数为(
)
A.90°
B.70°
C.60°
D.45°
6.下列说法中,正确的个数有(
)
①三角形具有稳定性;
②如果两个角相等,那么这两个角是对顶角;
③三角形的角平分线是射线;
④直线外一点到这条直线的垂线段叫做这点到直线的距离;
⑤任何一个三角形都有三条高、三条中线、三条角平分线;
⑥三角形的三条角平分线交于一点,且这点在三角形内.
A.2
B.3
C.4
D.5
7.如图,已知:△AFD和△CEB,点A,E,F,C在同一直线上,在给出的下列条件中,①AE=CF,②∠D=∠B,③AD=CB,④DF∥BE,选出三个条件可以证明△AFD≌△CEB的有____组(
)
A.4
B.3
C.2
D.1
8.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC.其中正确的结论是(
)
A.①②
B.①②③
C.①③
D.②③
三、解答题
9.(1)如图,已知△ADC中,∠A=30°,∠ADC=110°,BE⊥AC,垂足为E,求∠B的度数.
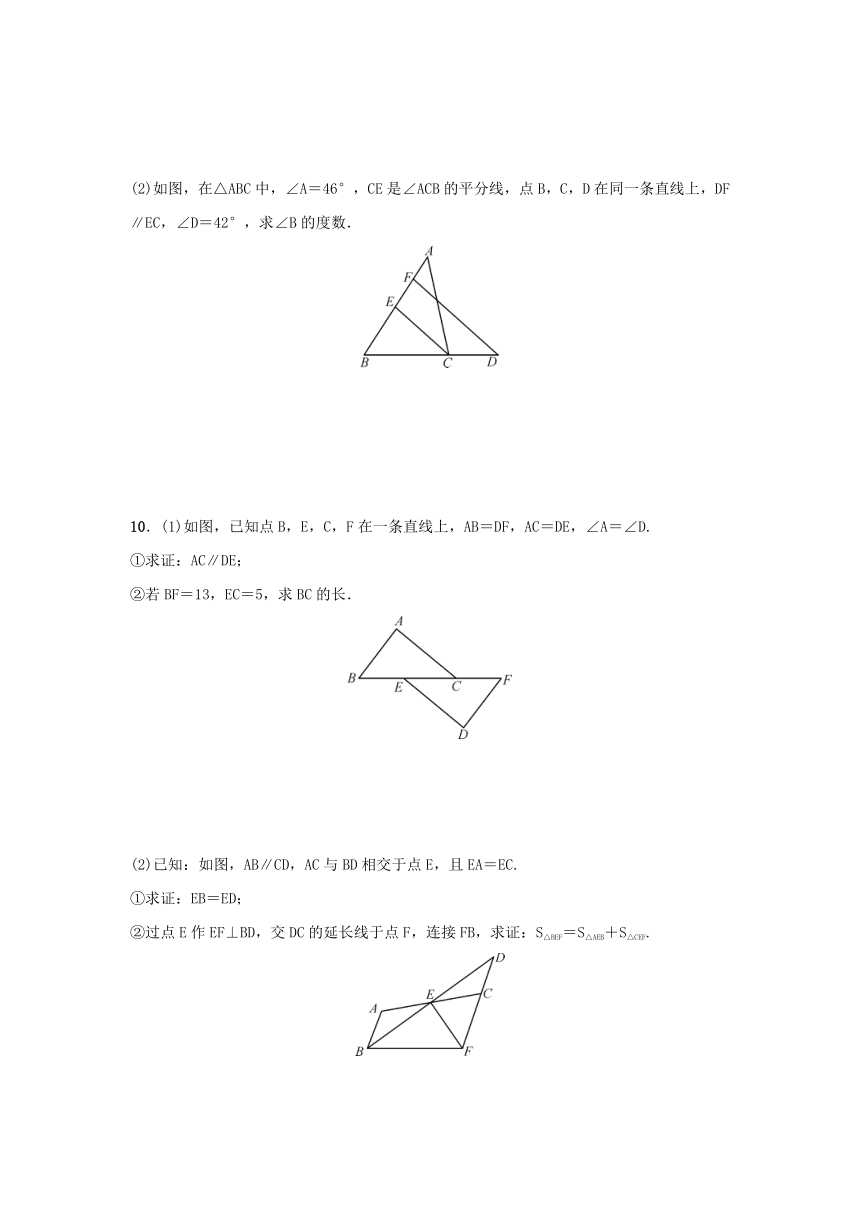
(2)如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,点B,C,D在同一条直线上,DF∥EC,∠D=42°,求∠B的度数.
10.(1)如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
①求证:AC∥DE;
②若BF=13,EC=5,求BC的长.
(2)已知:如图,AB∥CD,AC与BD相交于点E,且EA=EC.
①求证:EB=ED;
②过点E作EF⊥BD,交DC的延长线于点F,连接FB,求证:S△BEF=S△AEB+S△CEF.
B组(中档题)
一、填空题
11.如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m-n=_________.
12.如果在一个三角形中一个角等于另一个角的2倍,那么我们称这个三角形为“倍角三角形”.已知“倍角三角形”中一个角为50°,则这个“倍角三角形”中最大角的度数为_________.
13.如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,则∠AOB的度数为_________.
二、解答题
14.如图1,∠ACB=90°,点D在AC上,DE⊥AB,垂足为E,交BC的延长线于点F,DE=EB,EG=EB.
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图2,找出图中与AB相等的线段,并证明.
图1 图2
C组(综合题)
15.在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE=_________度;
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段BC上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时α与β之间的数量关系(不需证明)
参考答案
2020-2021学年北师大版七年级数学下册第四章
三角形
章末同步单元练习题
A组(基础题)
一、填空题
1.如图,在△ABC中,BD=DE=EC,则AD,AE分别是△ABE和△ADC的中线.
2.(1)三角形的三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是等边三角形.
(2)已知AD为△ABC的中线,AB=5
cm,且△ACD的周长比△ABD的周长少2
cm,则AC=3_cm.
3.如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=52°.
4.(1)等腰三角形有两边长分别为5和10,则它的周长为25.
(2)(2020·成都青羊区期末)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD交AD的延长线于点E.若∠DBE=25°,则∠CAB=50°.
二、选择题
5.已知直线a∥b,Rt△DCB按如图所示的方式放置,点C在直线b上,∠DCB=90°,若∠B=20°,则∠1+∠2的度数为(B)
A.90°
B.70°
C.60°
D.45°
6.下列说法中,正确的个数有(B)
①三角形具有稳定性;
②如果两个角相等,那么这两个角是对顶角;
③三角形的角平分线是射线;
④直线外一点到这条直线的垂线段叫做这点到直线的距离;
⑤任何一个三角形都有三条高、三条中线、三条角平分线;
⑥三角形的三条角平分线交于一点,且这点在三角形内.
A.2
B.3
C.4
D.5
7.如图,已知:△AFD和△CEB,点A,E,F,C在同一直线上,在给出的下列条件中,①AE=CF,②∠D=∠B,③AD=CB,④DF∥BE,选出三个条件可以证明△AFD≌△CEB的有____组(C)
A.4
B.3
C.2
D.1
8.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC.其中正确的结论是(B)
A.①②
B.①②③
C.①③
D.②③
三、解答题
9.(1)如图,已知△ADC中,∠A=30°,∠ADC=110°,BE⊥AC,垂足为E,求∠B的度数.
解:在△ADC中,∠A=30°,∠ADC=110°,
∴∠C=180°-∠A-∠ADC=40°.
∵BE⊥AC,∴∠BEC=90°.
∴∠B=90°-∠C=50°.
(2)如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,点B,C,D在同一条直线上,DF∥EC,∠D=42°,求∠B的度数.
解:∵FD∥EC,
∴∠BCE=∠D=42°.
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°.
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
10.(1)如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
①求证:AC∥DE;
②若BF=13,EC=5,求BC的长.
解:①证明:在△ABC和△DFE中,
∴△ABC≌△DFE(SAS).
∴∠ACE=∠DEF.
∴AC∥DE.
②∵△ABC≌△DFE,
∴BC=EF.
∴CB-EC=EF-EC,即EB=CF.
∵BF=13,EC=5,∴EB==4.
∴CB=4+5=9.
(2)已知:如图,AB∥CD,AC与BD相交于点E,且EA=EC.
①求证:EB=ED;
②过点E作EF⊥BD,交DC的延长线于点F,连接FB,求证:S△BEF=S△AEB+S△CEF.
证明:①∵AB∥CD,
∴∠ABE=∠D.
在△ABE和△CDE中,
∴△ABE≌△CDE(AAS).
∴EB=ED.
②∵△ABE≌△CDE,
∴S△AEB=S△DEC.
∵EB=ED,
∴S△BEF=S△DEF.
∵S△DEF=S△DEC+S△CEF,
∴S△BEF=S△AEB+S△CEF.
B组(中档题)
一、填空题
11.如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m-n=3.
12.如果在一个三角形中一个角等于另一个角的2倍,那么我们称这个三角形为“倍角三角形”.已知“倍角三角形”中一个角为50°,则这个“倍角三角形”中最大角的度数为100°或()°或105°.
13.如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,则∠AOB的度数为110°.
二、解答题
14.如图1,∠ACB=90°,点D在AC上,DE⊥AB,垂足为E,交BC的延长线于点F,DE=EB,EG=EB.
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图2,找出图中与AB相等的线段,并证明.
图1 图2
解:(1)证明:∵DE=EB,EG=EB,DE⊥AB,
∴DE-EB=EG.
∴∠EGD=∠EDG=∠EDB=∠EBD=45°.
∴∠AGD=∠FDB=135°.
∵∠ACB=90°,∠AED=90°,∠ADE=∠FDC,
∴∠A=∠F.
∴∠ADG=∠FBD.
在△ADG和△FDB中,
∴△ADG≌△FBD(ASA).
∴AG=DF.
(2)AB=DM.证明如下:
∵DE=EB,EG=EB,
∴DE=EB=EG.
∵DE⊥AB,∴∠AED=∠MEG=90°.
在△AED和△MEG中,
∴△AED≌△MEG(AAS).
∴AE=ME.
∴AE+EB=EM+DE,
即AB=DM.
C组(综合题)
15.在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE=90度;
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段BC上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时α与β之间的数量关系(不需证明)
解:①α+β=180°.证明:
∵∠BAC=∠DAE,
∴∠BAD+∠DAC=∠DAC+∠CAE.
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
∴∠ACE=∠B.
∵∠B+∠ACB=180°-α,
∴∠DCE=∠ACE+∠ACB=180°-α=β.
∴α+β=180°.
②补充图形如图,α=β.
三角形
章末同步单元练习题
A组(基础题)
一、填空题
1.如图,在△ABC中,BD=DE=EC,则AD,AE分别是___________的中线.
2.(1)三角形的三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是_________三角形.
(2)已知AD为△ABC的中线,AB=5
cm,且△ACD的周长比△ABD的周长少2
cm,则AC=_________.
3.如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=_________.
4.(1)等腰三角形有两边长分别为5和10,则它的周长为_________.
(2)(2020·成都青羊区期末)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD交AD的延长线于点E.若∠DBE=25°,则∠CAB=_________.
二、选择题
5.已知直线a∥b,Rt△DCB按如图所示的方式放置,点C在直线b上,∠DCB=90°,若∠B=20°,则∠1+∠2的度数为(
)
A.90°
B.70°
C.60°
D.45°
6.下列说法中,正确的个数有(
)
①三角形具有稳定性;
②如果两个角相等,那么这两个角是对顶角;
③三角形的角平分线是射线;
④直线外一点到这条直线的垂线段叫做这点到直线的距离;
⑤任何一个三角形都有三条高、三条中线、三条角平分线;
⑥三角形的三条角平分线交于一点,且这点在三角形内.
A.2
B.3
C.4
D.5
7.如图,已知:△AFD和△CEB,点A,E,F,C在同一直线上,在给出的下列条件中,①AE=CF,②∠D=∠B,③AD=CB,④DF∥BE,选出三个条件可以证明△AFD≌△CEB的有____组(
)
A.4
B.3
C.2
D.1
8.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC.其中正确的结论是(
)
A.①②
B.①②③
C.①③
D.②③
三、解答题
9.(1)如图,已知△ADC中,∠A=30°,∠ADC=110°,BE⊥AC,垂足为E,求∠B的度数.
(2)如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,点B,C,D在同一条直线上,DF∥EC,∠D=42°,求∠B的度数.
10.(1)如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
①求证:AC∥DE;
②若BF=13,EC=5,求BC的长.
(2)已知:如图,AB∥CD,AC与BD相交于点E,且EA=EC.
①求证:EB=ED;
②过点E作EF⊥BD,交DC的延长线于点F,连接FB,求证:S△BEF=S△AEB+S△CEF.
B组(中档题)
一、填空题
11.如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m-n=_________.
12.如果在一个三角形中一个角等于另一个角的2倍,那么我们称这个三角形为“倍角三角形”.已知“倍角三角形”中一个角为50°,则这个“倍角三角形”中最大角的度数为_________.
13.如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,则∠AOB的度数为_________.
二、解答题
14.如图1,∠ACB=90°,点D在AC上,DE⊥AB,垂足为E,交BC的延长线于点F,DE=EB,EG=EB.
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图2,找出图中与AB相等的线段,并证明.
图1 图2
C组(综合题)
15.在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE=_________度;
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段BC上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时α与β之间的数量关系(不需证明)
参考答案
2020-2021学年北师大版七年级数学下册第四章
三角形
章末同步单元练习题
A组(基础题)
一、填空题
1.如图,在△ABC中,BD=DE=EC,则AD,AE分别是△ABE和△ADC的中线.
2.(1)三角形的三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是等边三角形.
(2)已知AD为△ABC的中线,AB=5
cm,且△ACD的周长比△ABD的周长少2
cm,则AC=3_cm.
3.如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=52°.
4.(1)等腰三角形有两边长分别为5和10,则它的周长为25.
(2)(2020·成都青羊区期末)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD交AD的延长线于点E.若∠DBE=25°,则∠CAB=50°.
二、选择题
5.已知直线a∥b,Rt△DCB按如图所示的方式放置,点C在直线b上,∠DCB=90°,若∠B=20°,则∠1+∠2的度数为(B)
A.90°
B.70°
C.60°
D.45°
6.下列说法中,正确的个数有(B)
①三角形具有稳定性;
②如果两个角相等,那么这两个角是对顶角;
③三角形的角平分线是射线;
④直线外一点到这条直线的垂线段叫做这点到直线的距离;
⑤任何一个三角形都有三条高、三条中线、三条角平分线;
⑥三角形的三条角平分线交于一点,且这点在三角形内.
A.2
B.3
C.4
D.5
7.如图,已知:△AFD和△CEB,点A,E,F,C在同一直线上,在给出的下列条件中,①AE=CF,②∠D=∠B,③AD=CB,④DF∥BE,选出三个条件可以证明△AFD≌△CEB的有____组(C)
A.4
B.3
C.2
D.1
8.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC.其中正确的结论是(B)
A.①②
B.①②③
C.①③
D.②③
三、解答题
9.(1)如图,已知△ADC中,∠A=30°,∠ADC=110°,BE⊥AC,垂足为E,求∠B的度数.
解:在△ADC中,∠A=30°,∠ADC=110°,
∴∠C=180°-∠A-∠ADC=40°.
∵BE⊥AC,∴∠BEC=90°.
∴∠B=90°-∠C=50°.
(2)如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,点B,C,D在同一条直线上,DF∥EC,∠D=42°,求∠B的度数.
解:∵FD∥EC,
∴∠BCE=∠D=42°.
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°.
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
10.(1)如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
①求证:AC∥DE;
②若BF=13,EC=5,求BC的长.
解:①证明:在△ABC和△DFE中,
∴△ABC≌△DFE(SAS).
∴∠ACE=∠DEF.
∴AC∥DE.
②∵△ABC≌△DFE,
∴BC=EF.
∴CB-EC=EF-EC,即EB=CF.
∵BF=13,EC=5,∴EB==4.
∴CB=4+5=9.
(2)已知:如图,AB∥CD,AC与BD相交于点E,且EA=EC.
①求证:EB=ED;
②过点E作EF⊥BD,交DC的延长线于点F,连接FB,求证:S△BEF=S△AEB+S△CEF.
证明:①∵AB∥CD,
∴∠ABE=∠D.
在△ABE和△CDE中,
∴△ABE≌△CDE(AAS).
∴EB=ED.
②∵△ABE≌△CDE,
∴S△AEB=S△DEC.
∵EB=ED,
∴S△BEF=S△DEF.
∵S△DEF=S△DEC+S△CEF,
∴S△BEF=S△AEB+S△CEF.
B组(中档题)
一、填空题
11.如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m-n=3.
12.如果在一个三角形中一个角等于另一个角的2倍,那么我们称这个三角形为“倍角三角形”.已知“倍角三角形”中一个角为50°,则这个“倍角三角形”中最大角的度数为100°或()°或105°.
13.如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,则∠AOB的度数为110°.
二、解答题
14.如图1,∠ACB=90°,点D在AC上,DE⊥AB,垂足为E,交BC的延长线于点F,DE=EB,EG=EB.
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图2,找出图中与AB相等的线段,并证明.
图1 图2
解:(1)证明:∵DE=EB,EG=EB,DE⊥AB,
∴DE-EB=EG.
∴∠EGD=∠EDG=∠EDB=∠EBD=45°.
∴∠AGD=∠FDB=135°.
∵∠ACB=90°,∠AED=90°,∠ADE=∠FDC,
∴∠A=∠F.
∴∠ADG=∠FBD.
在△ADG和△FDB中,
∴△ADG≌△FBD(ASA).
∴AG=DF.
(2)AB=DM.证明如下:
∵DE=EB,EG=EB,
∴DE=EB=EG.
∵DE⊥AB,∴∠AED=∠MEG=90°.
在△AED和△MEG中,
∴△AED≌△MEG(AAS).
∴AE=ME.
∴AE+EB=EM+DE,
即AB=DM.
C组(综合题)
15.在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE=90度;
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段BC上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时α与β之间的数量关系(不需证明)
解:①α+β=180°.证明:
∵∠BAC=∠DAE,
∴∠BAD+∠DAC=∠DAC+∠CAE.
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
∴∠ACE=∠B.
∵∠B+∠ACB=180°-α,
∴∠DCE=∠ACE+∠ACB=180°-α=β.
∴α+β=180°.
②补充图形如图,α=β.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
