2020-2021学年华东师大版八年级数学下册:第17章函数及其图像复习课课件(共22张ppt)
文档属性
| 名称 | 2020-2021学年华东师大版八年级数学下册:第17章函数及其图像复习课课件(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 337.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 21:11:54 | ||
图片预览







文档简介
(共20张PPT)
1.课本
2.导学案
3.练习本
4.双色笔
全力投入会使你与众不同,你是优秀的,你一定能做得更好!
课前准备
一般地,如果
y
=
k
x
+b
(k,
b为常数,k≠0),那么y叫做x的一次函数.
特别地,当b=0时,y
=
k
x
+b
就成为
y
=
k
x,这时,y叫做x的正比例函数.
注意:正比例函数是一种特殊的一次函数。
知识梳理
一、知识要点:
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
4、直线y=kx+b(k≠0)的图象可以由y=kx(k≠0)的图象沿_________平移得到。
5、正比例函数y=k
x
(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
6、一次函数y=k
x
+
b
(k
≠
0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=k
x+
b(k
≠
0)的草图回答出各图
中k、b的符号:
k___0,b___0
k___0,b___0
k___0,b___0
k___0,b___0
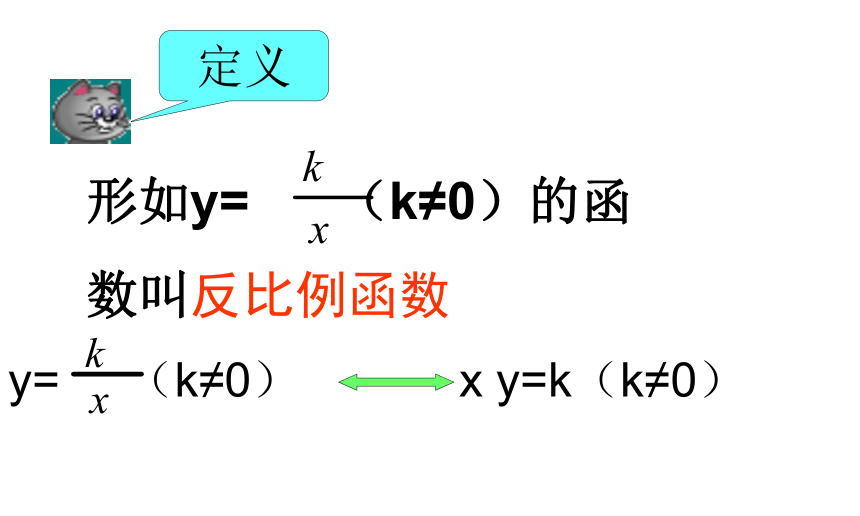
形如y=
(k≠0)的函
数叫反比例函数
定义
y=
(k≠0)
x
y=k(k≠0)
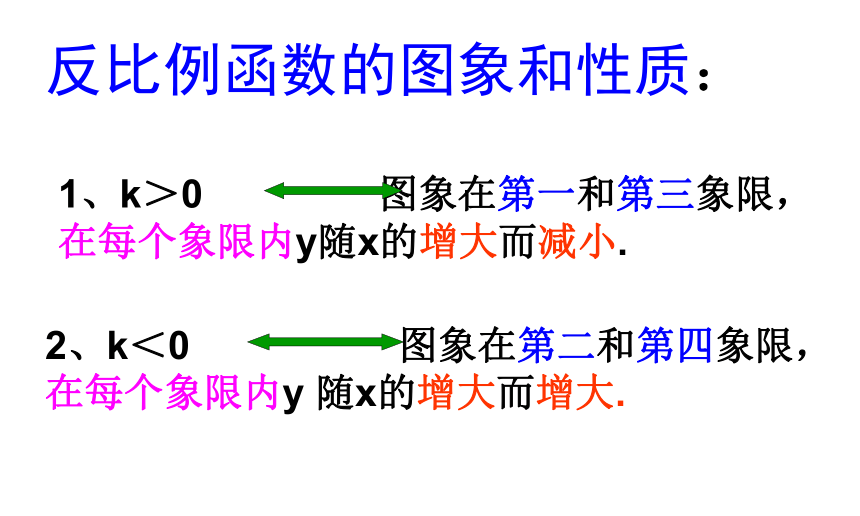
反比例函数的图象和性质:
1、k>0
图象在第一和第三象限,在每个象限内y随x的增大而减小.
2、k<0
图象在第二和第四象限,在每个象限内y
随x的增大而增大.
学以至用
数学来源于生活
生活离不开数学
十七章复习(二)
学习目标
1、熟练掌握一次函数、正比例函数、反比例函数的概念及它们的图像和性质以及一次函数的应用;
2、
通过小组合作,质疑探究,体会数形结合的思想;
3、
积极投入,全力以赴,培养细致认真的学习态度。
重点
:一次函数、正比例函数、反比例函数的图像和性质。
难点
:一次函数的应用。
预习反馈
1.优秀小组:
优秀个人:
2.存在的问题:
(1)、针对一次函数、反比例函数的性质掌握不好。
(2)、根据图像求反比例函数解析式掌握不好。
高效讨论、实现目标:6分钟
重点讨论:
1、一次函数、正比例函数、反比例函数的概念及它们的图像和性质、
2、一次函数的应用
3、预习中出现的问题
讨论方式:
1.先一对一讨论,再组内互相交流,疑问用红笔
标出,边讨论边
改错。
2.
注意总结题目的解题规律、方法和易错点
,规范步骤,多拓展,
注重知识的总结与掌握
。
3.
有展示点评任务的小组小组长做好展示、点评分工。
展示内容
展示小组
探究点一
组
拓展提升
组
探究点二
组
探究点三
1
组
探究点三
2
组
高效展示
要求:⑴口头展示,声音洪亮、清楚;书面展示要分层次、要点化,书写要认真、
规范。
⑵非展示同学巩固基础知识、整理落实学案,做好拓展。不浪费一分钟,小组长做好安排和检查。
要求:
⑴先点评对错,再点评思路方法,应该注意的问题,力争进行必要的变形拓展。
⑵其他同学认真倾听、积极思考、记好笔记、大胆质疑。
精彩点评
点评内容
点评小组
探究点一、拓展提升
组
探究点二
组
探究点三
1
组
探究点三
2
组
小试牛刀
下列函数中哪些是正比例函数?
①
②
③
④
⑤
⑥
⑦
⑧
y
=
3x-1
y
=
2x2
y
=
2x
3
y
=
x
1
y
=
3x
y
=
3
2x
y
=
1
3x
y
=
X
1
2、已知点P(x1,3)和点Q(-2,y1)满
足反比例函数y=
,则x1= ,y1= .
3、已知点P(2,-3)满足反比例函数
y=
,则k= .
x
k
1.
已知k<0,则函数
y1=k
x,
y2=
在同一坐标系中的图象大致是
(
)
x
y
0
x
y
0
x
y
0
x
y
0
(C)
(D)
(A)
(B)
2.若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数
的图象上,则(
)
A、y1>y2>y3
B、y2>y1>y3
C、y3>y1>y2
D、y3>y2>y1
能力提高
当堂检测
1、要求:独立完成
2、时间:2分钟左右
回扣目标
总结收获
课堂小结
函数
正比例函数
反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=k
x
(
k≠0
)
(
k是常数,k≠0
)
y
=
x
k
直线
双曲线
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
一三象限
二四象限
作
业
1、完善导学案
2、完成课本习题
谢谢
1.课本
2.导学案
3.练习本
4.双色笔
全力投入会使你与众不同,你是优秀的,你一定能做得更好!
课前准备
一般地,如果
y
=
k
x
+b
(k,
b为常数,k≠0),那么y叫做x的一次函数.
特别地,当b=0时,y
=
k
x
+b
就成为
y
=
k
x,这时,y叫做x的正比例函数.
注意:正比例函数是一种特殊的一次函数。
知识梳理
一、知识要点:
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
4、直线y=kx+b(k≠0)的图象可以由y=kx(k≠0)的图象沿_________平移得到。
5、正比例函数y=k
x
(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
6、一次函数y=k
x
+
b
(k
≠
0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=k
x+
b(k
≠
0)的草图回答出各图
中k、b的符号:
k___0,b___0
k___0,b___0
k___0,b___0
k___0,b___0
形如y=
(k≠0)的函
数叫反比例函数
定义
y=
(k≠0)
x
y=k(k≠0)
反比例函数的图象和性质:
1、k>0
图象在第一和第三象限,在每个象限内y随x的增大而减小.
2、k<0
图象在第二和第四象限,在每个象限内y
随x的增大而增大.
学以至用
数学来源于生活
生活离不开数学
十七章复习(二)
学习目标
1、熟练掌握一次函数、正比例函数、反比例函数的概念及它们的图像和性质以及一次函数的应用;
2、
通过小组合作,质疑探究,体会数形结合的思想;
3、
积极投入,全力以赴,培养细致认真的学习态度。
重点
:一次函数、正比例函数、反比例函数的图像和性质。
难点
:一次函数的应用。
预习反馈
1.优秀小组:
优秀个人:
2.存在的问题:
(1)、针对一次函数、反比例函数的性质掌握不好。
(2)、根据图像求反比例函数解析式掌握不好。
高效讨论、实现目标:6分钟
重点讨论:
1、一次函数、正比例函数、反比例函数的概念及它们的图像和性质、
2、一次函数的应用
3、预习中出现的问题
讨论方式:
1.先一对一讨论,再组内互相交流,疑问用红笔
标出,边讨论边
改错。
2.
注意总结题目的解题规律、方法和易错点
,规范步骤,多拓展,
注重知识的总结与掌握
。
3.
有展示点评任务的小组小组长做好展示、点评分工。
展示内容
展示小组
探究点一
组
拓展提升
组
探究点二
组
探究点三
1
组
探究点三
2
组
高效展示
要求:⑴口头展示,声音洪亮、清楚;书面展示要分层次、要点化,书写要认真、
规范。
⑵非展示同学巩固基础知识、整理落实学案,做好拓展。不浪费一分钟,小组长做好安排和检查。
要求:
⑴先点评对错,再点评思路方法,应该注意的问题,力争进行必要的变形拓展。
⑵其他同学认真倾听、积极思考、记好笔记、大胆质疑。
精彩点评
点评内容
点评小组
探究点一、拓展提升
组
探究点二
组
探究点三
1
组
探究点三
2
组
小试牛刀
下列函数中哪些是正比例函数?
①
②
③
④
⑤
⑥
⑦
⑧
y
=
3x-1
y
=
2x2
y
=
2x
3
y
=
x
1
y
=
3x
y
=
3
2x
y
=
1
3x
y
=
X
1
2、已知点P(x1,3)和点Q(-2,y1)满
足反比例函数y=
,则x1= ,y1= .
3、已知点P(2,-3)满足反比例函数
y=
,则k= .
x
k
1.
已知k<0,则函数
y1=k
x,
y2=
在同一坐标系中的图象大致是
(
)
x
y
0
x
y
0
x
y
0
x
y
0
(C)
(D)
(A)
(B)
2.若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数
的图象上,则(
)
A、y1>y2>y3
B、y2>y1>y3
C、y3>y1>y2
D、y3>y2>y1
能力提高
当堂检测
1、要求:独立完成
2、时间:2分钟左右
回扣目标
总结收获
课堂小结
函数
正比例函数
反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=k
x
(
k≠0
)
(
k是常数,k≠0
)
y
=
x
k
直线
双曲线
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
一三象限
二四象限
作
业
1、完善导学案
2、完成课本习题
谢谢
