3.3相似三角形的性质和判定课件

(共14张PPT)
3.3 相似三角形
的性质和预备判定
永华中学
A
B
C
D
E
蓦然回首
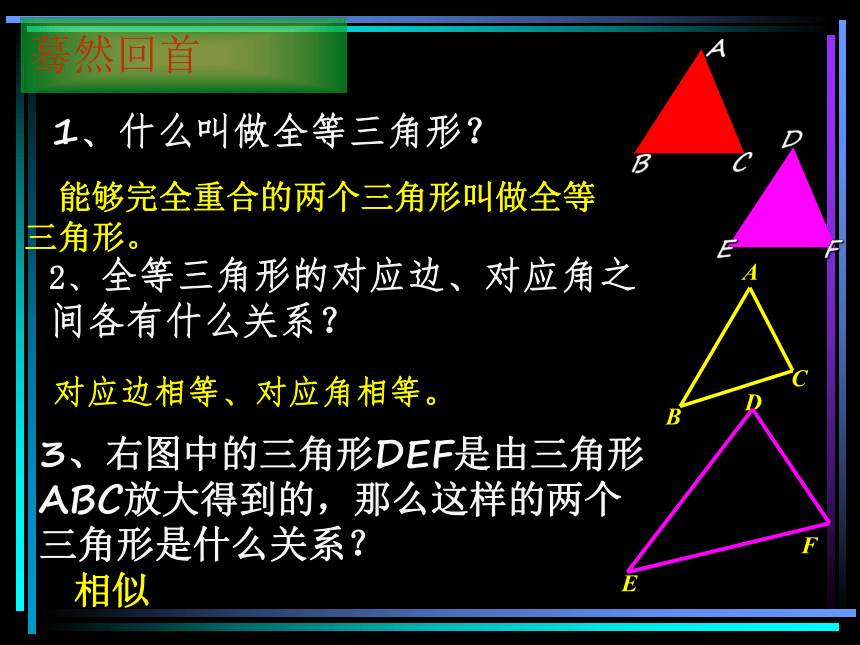
1、什么叫做全等三角形？
能够完全重合的两个三角形叫做全等三角形。
2、全等三角形的对应边、对应角之间各有什么关系？
对应边相等、对应角相等。
A
B
C
D
E
F
A
B
C
E
D
F
3、右图中的三角形DEF是由三角形
ABC放大得到的，那么这样的两个
三角形是什么关系？
相似
A
B
C
E
D
F
1㎝
1.5㎝
1.3㎝
2㎝
3㎝
2.6㎝
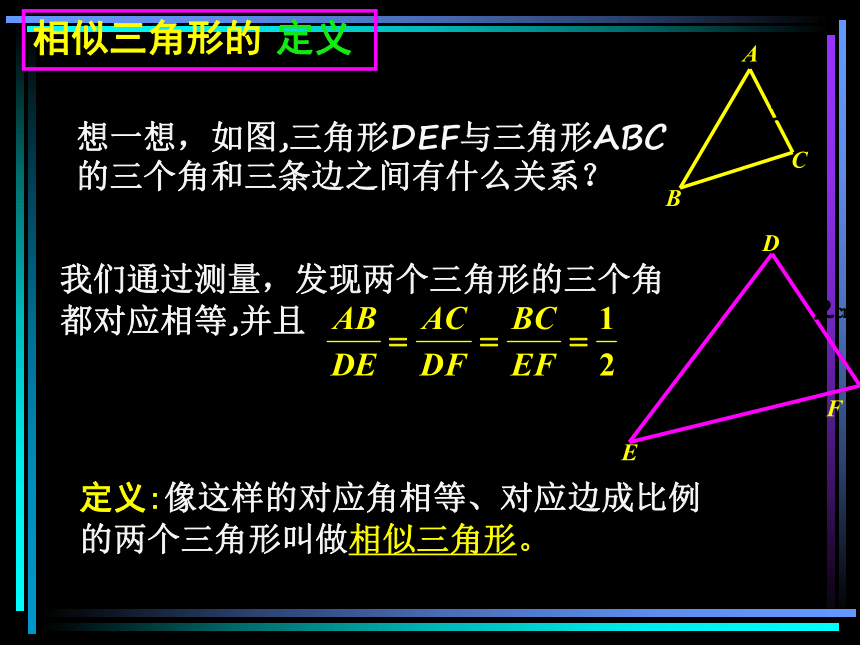
想一想，如图,三角形DEF与三角形ABC
的三个角和三条边之间有什么关系？
我们通过测量，发现两个三角形的三个角
都对应相等,并且
定义:像这样的对应角相等、对应边成比例
的两个三角形叫做相似三角形。
相似三角形的 定义
探究新知
A
B
C
E
D
F
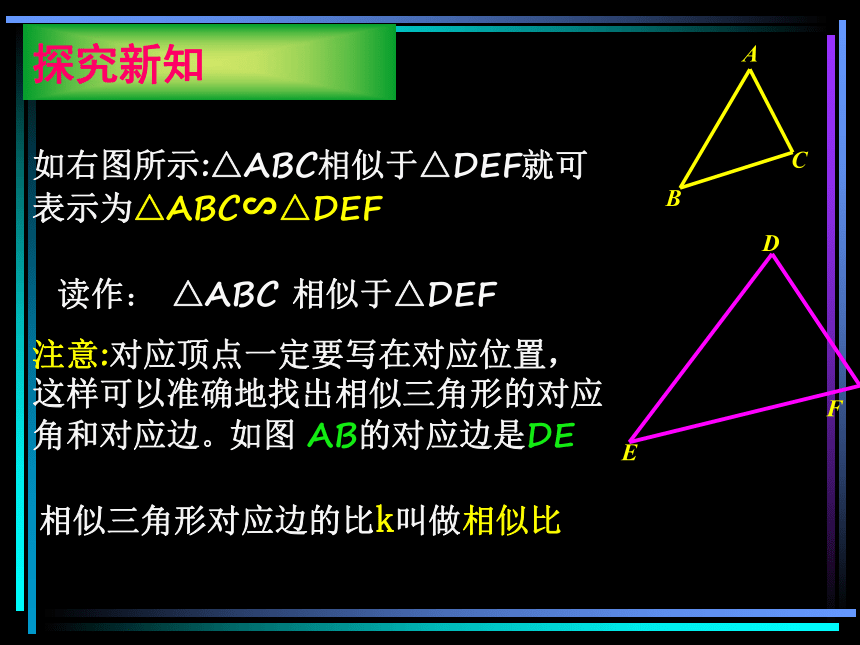
读作： △ABC 相似于△DEF
如右图所示:△ABC相似于△DEF就可表示为△ABC∽△DEF
注意:对应顶点一定要写在对应位置，这样可以准确地找出相似三角形的对应角和对应边。如图,AB的对应边是DE
相似三角形对应边的比k叫做相似比
证明: ∵
∠A= ∠D
∠B=∠F
∠C=∠E
∴
△ ABC∽ △ DEF
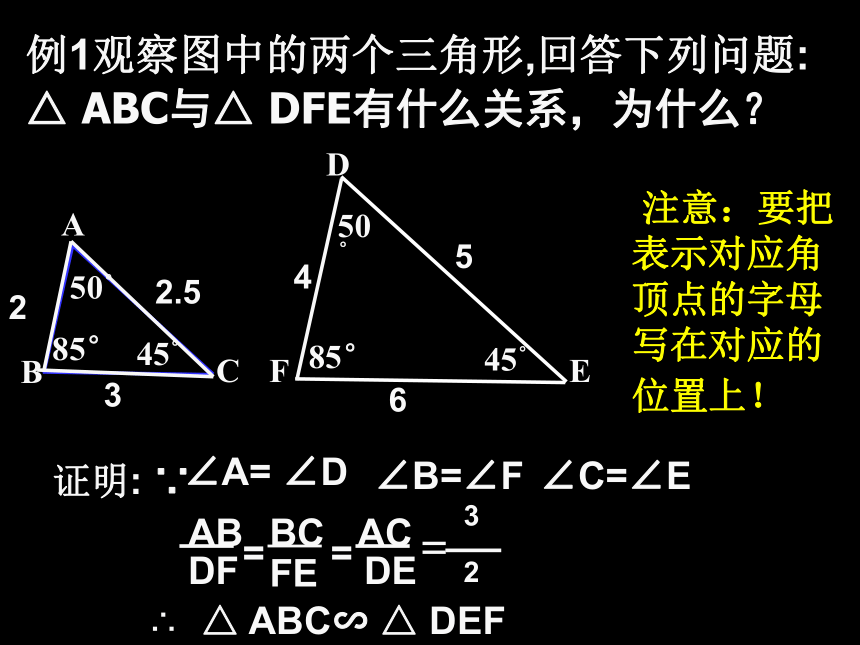
注意：要把表示对应角顶点的字母写在对应的位置上！
例1观察图中的两个三角形,回答下列问题: △ ABC与△ DFE有什么关系，为什么？
D
E
F
45°
85°
50°
6
A
B
C
45°
85°
50°
3
2
4
2.5
5
AB
DF
=
BC
AC
=
DE
FE
=
3
2
A
c
B
D
E
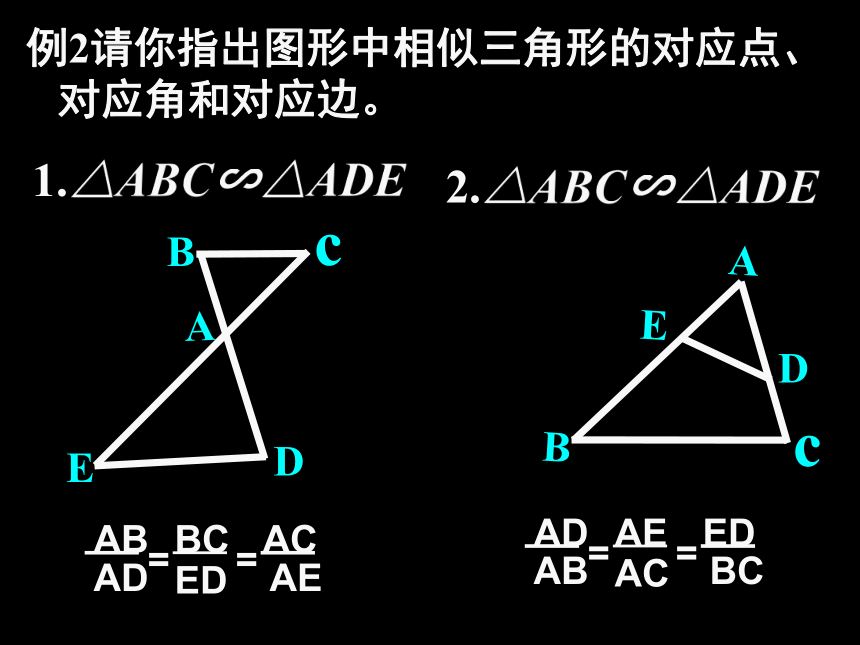
1.△ABC∽△ADE
c
A
B
D
E
2.△ABC∽△ADE
例2请你指出图形中相似三角形的对应点、对应角和对应边。
AB
AD
=
BC
AC
=
AE
ED
AD
AB
=
AE
ED
=
BC
AC
x
20
33
48
22
30
B
A
E
D
C
　例３．在下面的图形中，有两个相似三角形， △ABC∽△ADE，试确定x的值。
例４.在下面的图形中，有两个相似三角形， △ABC∽△DEF，试确定 y、m、n的值。
A
C
m°
50°
45°
2a
y
D
E
F
45°
85°
3a
10
n°
B
例5.△ ABC与△ DEF相似,且相似比是
则△ DEF 与△ ABC的相似比是( )
2
3
A
2
3
B
4
9
C
3
2
D
2
3
C
注意：相似比是有顺序的．
若两相似三角形△ABC与△A`B`C`的相似比为k1， △A`B`C`与△ABC的相似比为k2，则
k1 k2 ＝1。
平行于三角形一边的直线和其他两边(或两边的延长线)相交所构成的三角形与三角形相似吗 为什么
猜猜看!
A
B
C
D
E
F
已知:DE∥BC
求证:△ADE∽△ABC
∴
证明:
过点作EF∥AB
∴四边形DBFE是平行四边形
∴DE=BF
∵DE ∥BC
∴
又∵ EF∥AB
又∠A=∠A,∠ADE=∠B, ∠AED=∠C
∴△ADE∽△ABC
∴
预备定理：平行于三角形一边的直线
和其他两边相交，所构成的三角形与
原三角形相似
∵ DE∥BC
∴ △ADE ∽△ABC
A
B
C
D
E
１、如图，
ＤＥ∥ＦＧ∥ＢＣ，
图中共有相似
三角形（　　）对。
Ａ
Ｂ
Ｃ
Ｇ
Ｅ
Ｄ
Ｆ
2、如图在平行四边形ABCD中，E
为AD上一点，连结CE并延长交BA
的延长线于点F，请找出相似的三角
形并表示出来。
小结：
2、相似三角形判定的预备定理
全等三角形
对应角
对应边
表示符号
相等
相等
相等
成比例
≌
∽
相似三角形
1、
平行于三角形一边的直线和其他两边相交，
所构成的三角形与原三角形相似