4.1.3 认识三角形课件(共25张PPT)
文档属性
| 名称 | 4.1.3 认识三角形课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 00:00:00 | ||
图片预览







文档简介
第1节 认识三角形
(第3课时)
第四章 三角形
2021年春北师大版七年级数学下册
1 了解三角形的角平分线、中线的概念并掌握其性质,会用工具准确画出三角形的角平分线、中线; (重点)
2 学会用数学知识解决实际问题的能力.(重点)
学习目标
{ED083AE6-46FA-4A59-8FB0-9F97EB10719F}
定义
图示
垂线
线段中点
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
新课导入
三角形的中线
如图,用铅笔可以支起一张均匀的三角形卡片.
你知道怎样确定这个点的位置吗?
“重心”
探究新知
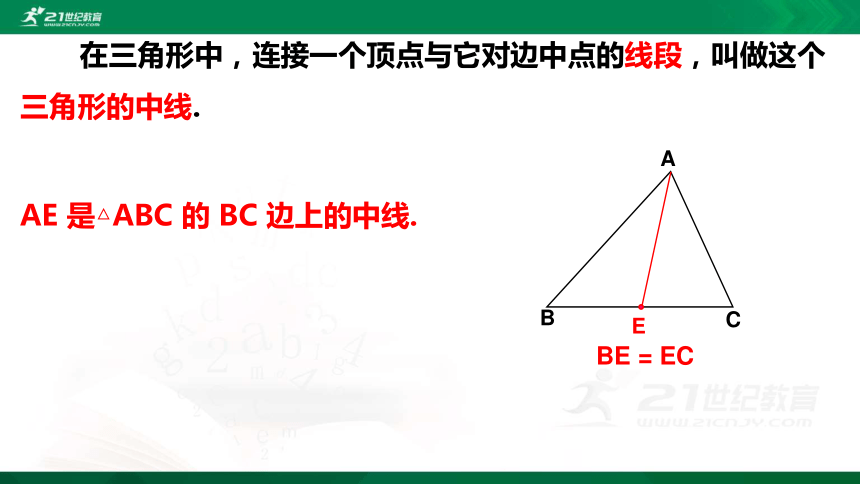
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线.
AE 是△ABC 的 BC 边上的中线.
A
B
C
E
BE = EC
2 表达方式:
(1)AD是△ABC中BC边上的中线.
(2)点D是BC边的中点.
(3)BD=DC或BD= BC或DC= BC
或BD=DC= BC.
拓展:如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?你能发现什么规律?
B
C
D
E
A
相等,因为两个三角形等底同高,所以它们面积相等.
发现:三角形的中线能将三角形的面积平分.
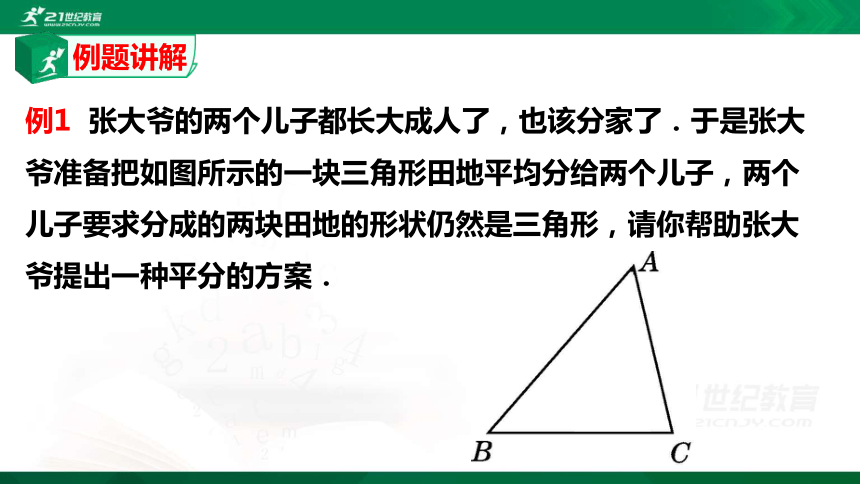
例1 张大爷的两个儿子都长大成人了,也该分家了.于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子,两个儿子要求分成的两块田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.
例题讲解
解:根据要求,平分田地的直线只能经过三角形的顶点.画△ABC的中线AD(如图),则AD就把△ABC的面积平分成两份.
这是因为AD是△ABC的中线,
所以BD=DC.过点A作AE⊥BC于点E.在△ABD和△ACD中,
因为BD,CD边上的高都是AE,
所以由三角形的面积计算公式,知△ABD和△ACD的面积相等,
因此,要把△ABC平分成两个三角形,只需画中线AD即可,这是
一种平分方法.
议一议
你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗?观察它们中线的交点你会发现什么规律?
发现:三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
O
O
O
任何三角形的三条中线都交于一点,且该点在三角形的内部,如图,这个点叫三角形的重心.
A
C
B
F
E
D
O
则AB边上的中线是______.
AC边上的中线是______.
CF
BE
AD
∵BE是中线
∴____=_____=
∴AB=2____=2____
∵CF是中线
AE
CE
AF
BF
BC边上的中线是______.
AC
1
2
例2 如图,点D、E、F分别是边BC、AC、AB上的中点
例题讲解
三角形的角平分线
如果现在你手上有一张画着一个三角形的薄纸,你能想办法画出它的一个内角的平分线吗?
你能通过折纸的方法得到它吗?
探究新知
将纸上画出的三角形剪下,将它的一个角对折, 使其两边重合.
折痕AD即为三角形的∠A的角平分线.
A
B
C
A
D
三角形的角平分线的定义
B
A
C
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
三角形的一个角的平分线叫做三角形的角平分线.这句话对吗?
D
∠1=∠2
1
2
“三角形的角平分线”是一条线段
每人准备锐角三角形、钝角三角形和直角三角形纸片各一个.
(1) 你能分别画出这三个三角形的三条角平分线吗?
(2) 你能用折纸的办法得到它们吗?
(3) 在每个三角形中,这三条角平分线之间有怎样的位置关系?
做一做
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴______=______ =12______
?
∴∠ACB=2______ =2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
三角形的三条角平分线线交于一点
例3 关于三角形的角平分线,下列说法正确的是( )
A.是线段
B.是射线
C.是直线
D.可以是射线或线段
A
例题讲解
1 三角形的角平分线是( )
A.直线 B.射线 C.线段 D.不确定
课堂练习
2 若AD是△ABC的中线,则下列结论中错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
3 如图, ∠1=∠2,∠3=∠4,下列结论错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
4 有一个三边均不等长的三角形,若在此三角形内找一点O,使得△OAB、△OAC、△OBC的面积相等.判断下列作法哪个正确?( )
A.做中线AD,再取AD的中点O
B.分别作中线AD、BE,再取两中线的交点O
C.分别作高线AD、DE,再取两高线交点O
D.分别作∠A 、∠B的角平分线,再取此两角平分线的交点O
5 如图,AE是△ABC的角平分线.已知∠B=45°,∠C=60°,求∠BAE和∠AEB的度数.
????
?
????
?
????
?
????
?
三角形重要线段
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
课堂小结
谢谢聆听
(第3课时)
第四章 三角形
2021年春北师大版七年级数学下册
1 了解三角形的角平分线、中线的概念并掌握其性质,会用工具准确画出三角形的角平分线、中线; (重点)
2 学会用数学知识解决实际问题的能力.(重点)
学习目标
{ED083AE6-46FA-4A59-8FB0-9F97EB10719F}
定义
图示
垂线
线段中点
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
新课导入
三角形的中线
如图,用铅笔可以支起一张均匀的三角形卡片.
你知道怎样确定这个点的位置吗?
“重心”
探究新知
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线.
AE 是△ABC 的 BC 边上的中线.
A
B
C
E
BE = EC
2 表达方式:
(1)AD是△ABC中BC边上的中线.
(2)点D是BC边的中点.
(3)BD=DC或BD= BC或DC= BC
或BD=DC= BC.
拓展:如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?你能发现什么规律?
B
C
D
E
A
相等,因为两个三角形等底同高,所以它们面积相等.
发现:三角形的中线能将三角形的面积平分.
例1 张大爷的两个儿子都长大成人了,也该分家了.于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子,两个儿子要求分成的两块田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.
例题讲解
解:根据要求,平分田地的直线只能经过三角形的顶点.画△ABC的中线AD(如图),则AD就把△ABC的面积平分成两份.
这是因为AD是△ABC的中线,
所以BD=DC.过点A作AE⊥BC于点E.在△ABD和△ACD中,
因为BD,CD边上的高都是AE,
所以由三角形的面积计算公式,知△ABD和△ACD的面积相等,
因此,要把△ABC平分成两个三角形,只需画中线AD即可,这是
一种平分方法.
议一议
你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗?观察它们中线的交点你会发现什么规律?
发现:三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
O
O
O
任何三角形的三条中线都交于一点,且该点在三角形的内部,如图,这个点叫三角形的重心.
A
C
B
F
E
D
O
则AB边上的中线是______.
AC边上的中线是______.
CF
BE
AD
∵BE是中线
∴____=_____=
∴AB=2____=2____
∵CF是中线
AE
CE
AF
BF
BC边上的中线是______.
AC
1
2
例2 如图,点D、E、F分别是边BC、AC、AB上的中点
例题讲解
三角形的角平分线
如果现在你手上有一张画着一个三角形的薄纸,你能想办法画出它的一个内角的平分线吗?
你能通过折纸的方法得到它吗?
探究新知
将纸上画出的三角形剪下,将它的一个角对折, 使其两边重合.
折痕AD即为三角形的∠A的角平分线.
A
B
C
A
D
三角形的角平分线的定义
B
A
C
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
三角形的一个角的平分线叫做三角形的角平分线.这句话对吗?
D
∠1=∠2
1
2
“三角形的角平分线”是一条线段
每人准备锐角三角形、钝角三角形和直角三角形纸片各一个.
(1) 你能分别画出这三个三角形的三条角平分线吗?
(2) 你能用折纸的办法得到它们吗?
(3) 在每个三角形中,这三条角平分线之间有怎样的位置关系?
做一做
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴______=______ =12______
?
∴∠ACB=2______ =2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
三角形的三条角平分线线交于一点
例3 关于三角形的角平分线,下列说法正确的是( )
A.是线段
B.是射线
C.是直线
D.可以是射线或线段
A
例题讲解
1 三角形的角平分线是( )
A.直线 B.射线 C.线段 D.不确定
课堂练习
2 若AD是△ABC的中线,则下列结论中错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
3 如图, ∠1=∠2,∠3=∠4,下列结论错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
4 有一个三边均不等长的三角形,若在此三角形内找一点O,使得△OAB、△OAC、△OBC的面积相等.判断下列作法哪个正确?( )
A.做中线AD,再取AD的中点O
B.分别作中线AD、BE,再取两中线的交点O
C.分别作高线AD、DE,再取两高线交点O
D.分别作∠A 、∠B的角平分线,再取此两角平分线的交点O
5 如图,AE是△ABC的角平分线.已知∠B=45°,∠C=60°,求∠BAE和∠AEB的度数.
????
?
????
?
????
?
????
?
三角形重要线段
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
