2020-2021学年七年级数学苏科版下册《第9章整式乘法与因式分解》课后能力提升作业(word附答案)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册《第9章整式乘法与因式分解》课后能力提升作业(word附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 58.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 21:03:17 | ||
图片预览



文档简介
2021年苏科版七年级数学下册《第9章整式乘法与因式分解》课后能力提升作业(附答案)
1.已知多项式ax+b与2x2+2x+3的乘积展开式中不含x的一次项,且常数项为﹣9,则ab的值为( )
A.
B.
C.﹣8
D.﹣6
2.已知x﹣y=3,xy=3,则(x+y)2的值为( )
A.24
B.18
C.21
D.12
3.下列运算中,不能用平方差公式运算的是( )
A.(﹣b﹣c)(﹣b+c)
B.﹣(x+y)(﹣x﹣y)
C.(x+y)(x﹣y)
D.(x+y)(2x﹣2y)
4.若x2+2(m﹣1)x+16是完全平方式,则m的值为( )
A.±8
B.﹣3或5
C.﹣3
D.5
5.已知:a+b=2,ab=﹣1,计算:(a﹣2)(b﹣2)的结果是( )
A.1
B.3
C.﹣1
D.﹣5
6.下列因式分解正确的是( )
A.x2﹣xy+y2=(x﹣y)2
B.x2﹣5x﹣6=(x﹣2)(x﹣3)
C.x3﹣4x=x(x2﹣4)
D.9m2﹣4n2=(3m+2n)(3m﹣2n)
7.若a=2020×2021+1,b=20202﹣2020×2021+20212,在下列判断结果正确是( )
A.a<b
B.a=b
C.a>b
D.无法判断
8.若a2﹣b2=,a+b=,则a﹣b的值为( )
A.
B.
C.
D.2
9.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
10.若实数x满足x2﹣2x﹣1=0,则2x3﹣7x2+4x+2023的值为( )
A.2020
B.2021
C.2022
D.2023
11.已知a,b,c是△ABC的三条边的长度,且满足a2﹣b2=c(a﹣b),
则△ABC一定是
三角形.
12.计算:108×112﹣1102的结果为
.
13.若(2x﹣a)(x+1)的积中不含x的一次项,则a的值为
.
14.分解因式:4a3b2﹣6a2b2=
.
15.分解因式:a2b﹣4ab+4b=
.
16.计算(x+2y﹣z)(x﹣2y+z)=
.
17.若a2+a﹣1=0,则a4+a3﹣2a2﹣a+2021的值为
.
18.设(2a+3b)2=(2a﹣3b)2+A,则A=
.
19.若ab=3,a﹣b=5,则2a2b﹣2ab2=
.
20.计算:2019×2021﹣20202=
.
21.因式分解:x3+3x2y﹣4x﹣12y.
22.因式分解:(x2+4x)2﹣2(x2+4x)﹣15.
23.先化简,再求值:(﹣x﹣2y)(2y﹣x)+(x+2y)2﹣x(2y﹣x),其中x=﹣,y=2.
24.先化简,再求值:(x﹣1)(x+1)+(2x﹣1)2﹣2x(2x﹣1),其中x=4.
25.已知(a+b)2=25,(a﹣b)2=9.求a2﹣6ab+b2.
26.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成相等的四个小长方形,然后按图②的方式拼成一个正方形.
(1)图②中阴影部分的正方形的边长等于
;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积:
方法一:
;
方法二:
;
(3)根据(2),直接写出(m﹣n)2,(m+n)2,mn这三个代数式之间的等量关系.
(4)根据(3)中的等量关系,解决如下问题:
对于任意的有理数x和y,若x+y=9,xy=18,求x﹣y的值.
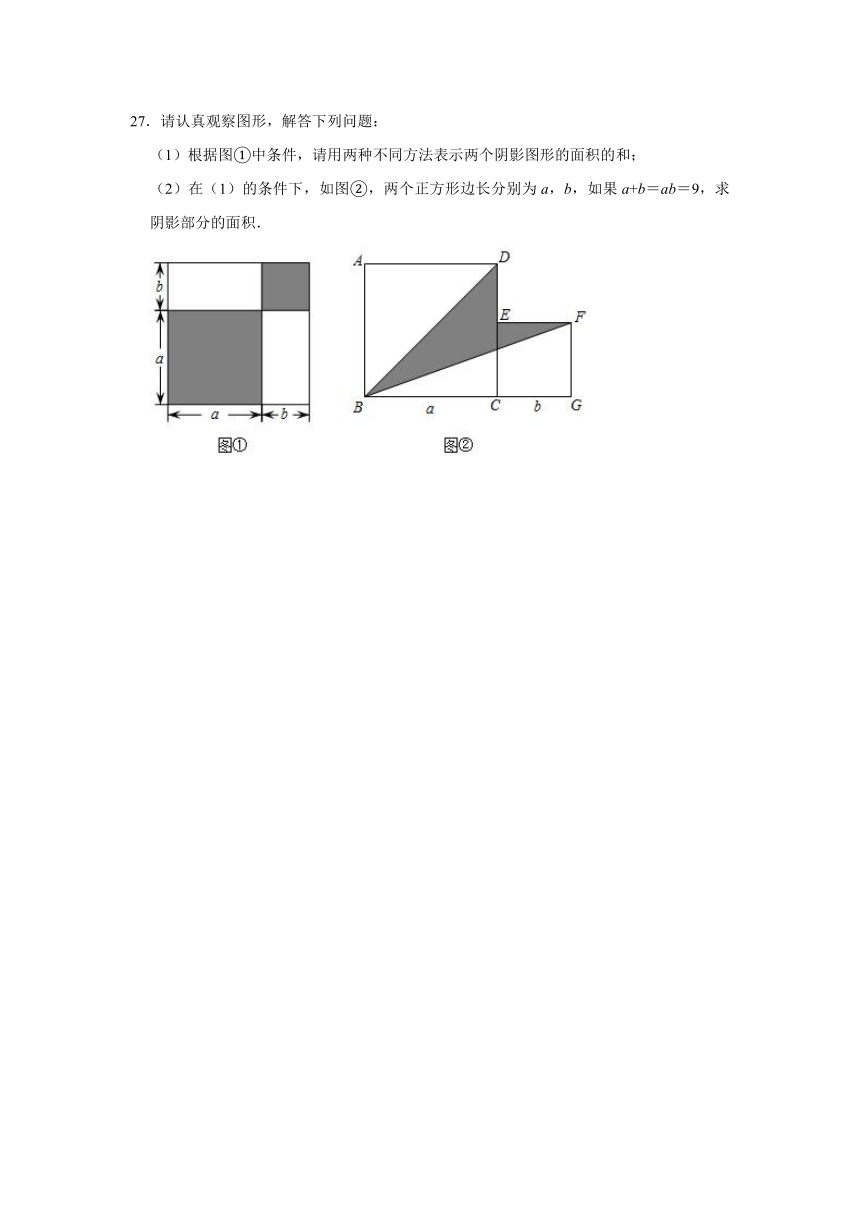
27.请认真观察图形,解答下列问题:
(1)根据图①中条件,请用两种不同方法表示两个阴影图形的面积的和;
(2)在(1)的条件下,如图②,两个正方形边长分别为a,b,如果a+b=ab=9,求阴影部分的面积.
参考答案
1.解:(ax+b)(2x2+2x+3)
=2ax3+2ax2+3ax+2bx2+2bx+3b
=2ax3+(2a+b)x2+(3a+2b)x+3b,
∵乘积展开式中不含x的一次项,且常数项为﹣9,
∴3a+2b=0且3b=﹣9,
则a=2,b=﹣3,
∴ab=2﹣3=,
故选:A.
2.解:∵x﹣y=3,xy=3,
∴(x+y)2=(x﹣y)2+4xy=32+4×3=21,故选:C.
3.解:A、(﹣b﹣c)(﹣b+c)符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意;
B、﹣(x+y)(﹣x﹣y)=(x+y)(x+y),不符合平方差公式的特点,不能用平方差公式计算,故本选项符合题意;
C、(x+y)(x﹣y)符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意;
D、(x+y)(2x﹣2y)=2(x+y)(x﹣y)符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意.
故选:B.
4.解:∵x2+2(m﹣1)x+16是完全平方式,而16=42,
∴m﹣1=4或m﹣1=﹣4,
∴m=5或﹣3.
故选:B.
5.解:∵a+b=2,ab=﹣1,
∴原式=ab﹣2a﹣2b+4
=ab﹣2(a+b)+4
=﹣1﹣4+4
=﹣1.
故选:C.
6.解:A、x2﹣xy+y2≠(x﹣y)2,因式分解错误,不符合题意.
B、x2﹣5x﹣6=(x﹣6)(x+1),因式分解错误,不符合题意.
C、x3﹣4x=x(x2﹣4)=x(x+2)(x﹣2),因式分解错误,不符合题意.
D、9m2﹣4n2=(3m+2n)(3m﹣2n),因式分解正确,符合题意.
故选:D.
7.解:a=2020×2021+1,
b=20202﹣2020×2021+20212
=(2020﹣2021)2+2020×2021
=2020×2021+1,
故a=b.
故选:B.
8.解:∵(a+b)(a﹣b)=a2﹣b2,
∴×(a﹣b)=,
∴a﹣b=.
故选:B.
9.解:多项式8a3b2+12a3bc﹣4a2b中各项的公因式是4a2b,
故选:C.
10.解:∵x2﹣2x﹣1=0,
∴2x3﹣7x2+4x+2023
=2x(x2﹣2x﹣1)﹣3(x2﹣2x﹣1)+2020
=2x×0﹣3×0+2020
=0+0+2020
=2020,
故选:A.
11.解:由a2﹣b2=c(a﹣b),
(a+b)(a﹣b)=c(a﹣b),
(a+b)(a﹣b)﹣c(a﹣b)=0,
(a﹣b)(a+b﹣c)=0,
∵三角形两边之和大于第三边,即a+b>c,
∴a+b﹣c≠0,
∴a﹣b=0,即a=b,
即△ABC一定是等腰三角形.
故答案为:等腰.
12.解:108×112﹣1102
=(110+2)(110﹣2)﹣1102
=1102﹣22﹣1102
=﹣4.
13.解:(2x﹣a)(x+1)=2x2+(2﹣a)x﹣a,
∵积中不含x的一次项,
∴2﹣a=0,
∴a=2,
故答案为:2.
14.解:4a3b2﹣6a2b2=2a2b2(2a﹣3).
故答案为:2a2b2(2a﹣3).
15.解:a2b﹣4ab+4b=b(a2﹣4a+4)=b(a﹣2)2
故答案为:b(a﹣2)2
16.解:(x+2y﹣z)(x﹣2y+z)
=x2﹣(2y﹣z)2
=x2﹣4y2+4yz﹣z2.
故答案是:x2﹣4y2+4yz﹣z2.
17.解:∵a2+a﹣1=0,
∴a4+a3﹣2a2﹣a+2021
=a2(a2+a﹣1)﹣(a2+a﹣1)+2020
=a2×0﹣0+2020
=0+0+2020
=2020,
故答案为:2020.
18.解:∵(2a+3b)2=4a2+12ab+9b2,
(2a﹣3b)2=4a2﹣12ab+9b2,
∴(2a+3b)2=(2a﹣3b)2+24ab,
∴A=24ab,
故答案为:24ab.
19.解:原式=2ab(a﹣b)=2×3×5=30,
故答案为:30.
20.解:2019×2021﹣20202
=(2020﹣1)×(2020+1)﹣20202=20202﹣1﹣20202=﹣1.
故答案为:﹣1.
21.解:x3+3x2y﹣4x﹣12y=(x3+3x2y)﹣(4x+12y)
=x2(x+3y)﹣4(x+3y)
=(x+3y)(x2﹣4)
=(x+3y)(x+2)(x﹣2).
22.解:原式=(x2+4x﹣5)(x2+4x+3)
=(x+5)(x﹣1)(x+3)(x+1).
23.解:原式=x2﹣4y2+x2+4xy+4y2﹣2xy+x2
=3x2+2xy,
当时,
原式=3×(﹣)2+2×(﹣)×2
=﹣.
24.解:原式=x2﹣1+4x2﹣4x+1﹣4x2+2x
=x2﹣2x,
当x=4时,原式=16﹣2×4=16﹣8=8.
25.解:因为(a+b)2=25,(a﹣b)2=9,
所以(a+b)2﹣(a﹣b)2=4ab=16,
所以a2﹣6ab+b2=(a﹣b)2﹣4ab=9﹣16=﹣7.
26.解:(1)图①被分割的四个小长方形的长为m,宽为n,拼成的图②整体是边长为m+n的正方形,中间是边长为m﹣n的小正方形,
故答案为:m﹣n;
(2)方法一:阴影部分是边长为m﹣n的正方形,因此面积为(m﹣n)2,
方法二:大正方形的面积减去四个长方形的面积,即(m+n)2﹣4mn,
故答案为:(m﹣n)2,(m+n)2﹣4mn;
(3)由(2)得,(m﹣n)2=(m+n)2﹣4mn;
答:(m﹣n)2,(m+n)2,mn这三个代数式之间的等量关系为(m﹣n)2=(m+n)2﹣4mn;
(4)由(3)得,(x﹣y)2=(x+y)2﹣4xy,
所以(x﹣y)2=92﹣4×18=9,
因此x﹣y=3或x﹣y=﹣3,
答:x﹣y的值为3或﹣3.
27.解:(1)方法一:两个正方形的面积和,即a2+b2,
方法二:边长为a+b的正方形的面积减去两个空白的长方形的面积,即(a+b)2﹣2ab,
因此有a2+b2=(a+b)2﹣2ab,
(2)图②阴影部分的面积是两个边长分别为a、b的正方形的面积和减去两个直角三角形的面积,
即a2+b2﹣a×a﹣(a+b)×b=a2+b2﹣ab=(a2+b2﹣ab)
=[(a+b)2﹣3ab],
当a+b=ab=9时,原式=×(81﹣27)=27,
答:阴影部分的面积为27.
1.已知多项式ax+b与2x2+2x+3的乘积展开式中不含x的一次项,且常数项为﹣9,则ab的值为( )
A.
B.
C.﹣8
D.﹣6
2.已知x﹣y=3,xy=3,则(x+y)2的值为( )
A.24
B.18
C.21
D.12
3.下列运算中,不能用平方差公式运算的是( )
A.(﹣b﹣c)(﹣b+c)
B.﹣(x+y)(﹣x﹣y)
C.(x+y)(x﹣y)
D.(x+y)(2x﹣2y)
4.若x2+2(m﹣1)x+16是完全平方式,则m的值为( )
A.±8
B.﹣3或5
C.﹣3
D.5
5.已知:a+b=2,ab=﹣1,计算:(a﹣2)(b﹣2)的结果是( )
A.1
B.3
C.﹣1
D.﹣5
6.下列因式分解正确的是( )
A.x2﹣xy+y2=(x﹣y)2
B.x2﹣5x﹣6=(x﹣2)(x﹣3)
C.x3﹣4x=x(x2﹣4)
D.9m2﹣4n2=(3m+2n)(3m﹣2n)
7.若a=2020×2021+1,b=20202﹣2020×2021+20212,在下列判断结果正确是( )
A.a<b
B.a=b
C.a>b
D.无法判断
8.若a2﹣b2=,a+b=,则a﹣b的值为( )
A.
B.
C.
D.2
9.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
10.若实数x满足x2﹣2x﹣1=0,则2x3﹣7x2+4x+2023的值为( )
A.2020
B.2021
C.2022
D.2023
11.已知a,b,c是△ABC的三条边的长度,且满足a2﹣b2=c(a﹣b),
则△ABC一定是
三角形.
12.计算:108×112﹣1102的结果为
.
13.若(2x﹣a)(x+1)的积中不含x的一次项,则a的值为
.
14.分解因式:4a3b2﹣6a2b2=
.
15.分解因式:a2b﹣4ab+4b=
.
16.计算(x+2y﹣z)(x﹣2y+z)=
.
17.若a2+a﹣1=0,则a4+a3﹣2a2﹣a+2021的值为
.
18.设(2a+3b)2=(2a﹣3b)2+A,则A=
.
19.若ab=3,a﹣b=5,则2a2b﹣2ab2=
.
20.计算:2019×2021﹣20202=
.
21.因式分解:x3+3x2y﹣4x﹣12y.
22.因式分解:(x2+4x)2﹣2(x2+4x)﹣15.
23.先化简,再求值:(﹣x﹣2y)(2y﹣x)+(x+2y)2﹣x(2y﹣x),其中x=﹣,y=2.
24.先化简,再求值:(x﹣1)(x+1)+(2x﹣1)2﹣2x(2x﹣1),其中x=4.
25.已知(a+b)2=25,(a﹣b)2=9.求a2﹣6ab+b2.
26.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成相等的四个小长方形,然后按图②的方式拼成一个正方形.
(1)图②中阴影部分的正方形的边长等于
;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积:
方法一:
;
方法二:
;
(3)根据(2),直接写出(m﹣n)2,(m+n)2,mn这三个代数式之间的等量关系.
(4)根据(3)中的等量关系,解决如下问题:
对于任意的有理数x和y,若x+y=9,xy=18,求x﹣y的值.
27.请认真观察图形,解答下列问题:
(1)根据图①中条件,请用两种不同方法表示两个阴影图形的面积的和;
(2)在(1)的条件下,如图②,两个正方形边长分别为a,b,如果a+b=ab=9,求阴影部分的面积.
参考答案
1.解:(ax+b)(2x2+2x+3)
=2ax3+2ax2+3ax+2bx2+2bx+3b
=2ax3+(2a+b)x2+(3a+2b)x+3b,
∵乘积展开式中不含x的一次项,且常数项为﹣9,
∴3a+2b=0且3b=﹣9,
则a=2,b=﹣3,
∴ab=2﹣3=,
故选:A.
2.解:∵x﹣y=3,xy=3,
∴(x+y)2=(x﹣y)2+4xy=32+4×3=21,故选:C.
3.解:A、(﹣b﹣c)(﹣b+c)符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意;
B、﹣(x+y)(﹣x﹣y)=(x+y)(x+y),不符合平方差公式的特点,不能用平方差公式计算,故本选项符合题意;
C、(x+y)(x﹣y)符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意;
D、(x+y)(2x﹣2y)=2(x+y)(x﹣y)符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意.
故选:B.
4.解:∵x2+2(m﹣1)x+16是完全平方式,而16=42,
∴m﹣1=4或m﹣1=﹣4,
∴m=5或﹣3.
故选:B.
5.解:∵a+b=2,ab=﹣1,
∴原式=ab﹣2a﹣2b+4
=ab﹣2(a+b)+4
=﹣1﹣4+4
=﹣1.
故选:C.
6.解:A、x2﹣xy+y2≠(x﹣y)2,因式分解错误,不符合题意.
B、x2﹣5x﹣6=(x﹣6)(x+1),因式分解错误,不符合题意.
C、x3﹣4x=x(x2﹣4)=x(x+2)(x﹣2),因式分解错误,不符合题意.
D、9m2﹣4n2=(3m+2n)(3m﹣2n),因式分解正确,符合题意.
故选:D.
7.解:a=2020×2021+1,
b=20202﹣2020×2021+20212
=(2020﹣2021)2+2020×2021
=2020×2021+1,
故a=b.
故选:B.
8.解:∵(a+b)(a﹣b)=a2﹣b2,
∴×(a﹣b)=,
∴a﹣b=.
故选:B.
9.解:多项式8a3b2+12a3bc﹣4a2b中各项的公因式是4a2b,
故选:C.
10.解:∵x2﹣2x﹣1=0,
∴2x3﹣7x2+4x+2023
=2x(x2﹣2x﹣1)﹣3(x2﹣2x﹣1)+2020
=2x×0﹣3×0+2020
=0+0+2020
=2020,
故选:A.
11.解:由a2﹣b2=c(a﹣b),
(a+b)(a﹣b)=c(a﹣b),
(a+b)(a﹣b)﹣c(a﹣b)=0,
(a﹣b)(a+b﹣c)=0,
∵三角形两边之和大于第三边,即a+b>c,
∴a+b﹣c≠0,
∴a﹣b=0,即a=b,
即△ABC一定是等腰三角形.
故答案为:等腰.
12.解:108×112﹣1102
=(110+2)(110﹣2)﹣1102
=1102﹣22﹣1102
=﹣4.
13.解:(2x﹣a)(x+1)=2x2+(2﹣a)x﹣a,
∵积中不含x的一次项,
∴2﹣a=0,
∴a=2,
故答案为:2.
14.解:4a3b2﹣6a2b2=2a2b2(2a﹣3).
故答案为:2a2b2(2a﹣3).
15.解:a2b﹣4ab+4b=b(a2﹣4a+4)=b(a﹣2)2
故答案为:b(a﹣2)2
16.解:(x+2y﹣z)(x﹣2y+z)
=x2﹣(2y﹣z)2
=x2﹣4y2+4yz﹣z2.
故答案是:x2﹣4y2+4yz﹣z2.
17.解:∵a2+a﹣1=0,
∴a4+a3﹣2a2﹣a+2021
=a2(a2+a﹣1)﹣(a2+a﹣1)+2020
=a2×0﹣0+2020
=0+0+2020
=2020,
故答案为:2020.
18.解:∵(2a+3b)2=4a2+12ab+9b2,
(2a﹣3b)2=4a2﹣12ab+9b2,
∴(2a+3b)2=(2a﹣3b)2+24ab,
∴A=24ab,
故答案为:24ab.
19.解:原式=2ab(a﹣b)=2×3×5=30,
故答案为:30.
20.解:2019×2021﹣20202
=(2020﹣1)×(2020+1)﹣20202=20202﹣1﹣20202=﹣1.
故答案为:﹣1.
21.解:x3+3x2y﹣4x﹣12y=(x3+3x2y)﹣(4x+12y)
=x2(x+3y)﹣4(x+3y)
=(x+3y)(x2﹣4)
=(x+3y)(x+2)(x﹣2).
22.解:原式=(x2+4x﹣5)(x2+4x+3)
=(x+5)(x﹣1)(x+3)(x+1).
23.解:原式=x2﹣4y2+x2+4xy+4y2﹣2xy+x2
=3x2+2xy,
当时,
原式=3×(﹣)2+2×(﹣)×2
=﹣.
24.解:原式=x2﹣1+4x2﹣4x+1﹣4x2+2x
=x2﹣2x,
当x=4时,原式=16﹣2×4=16﹣8=8.
25.解:因为(a+b)2=25,(a﹣b)2=9,
所以(a+b)2﹣(a﹣b)2=4ab=16,
所以a2﹣6ab+b2=(a﹣b)2﹣4ab=9﹣16=﹣7.
26.解:(1)图①被分割的四个小长方形的长为m,宽为n,拼成的图②整体是边长为m+n的正方形,中间是边长为m﹣n的小正方形,
故答案为:m﹣n;
(2)方法一:阴影部分是边长为m﹣n的正方形,因此面积为(m﹣n)2,
方法二:大正方形的面积减去四个长方形的面积,即(m+n)2﹣4mn,
故答案为:(m﹣n)2,(m+n)2﹣4mn;
(3)由(2)得,(m﹣n)2=(m+n)2﹣4mn;
答:(m﹣n)2,(m+n)2,mn这三个代数式之间的等量关系为(m﹣n)2=(m+n)2﹣4mn;
(4)由(3)得,(x﹣y)2=(x+y)2﹣4xy,
所以(x﹣y)2=92﹣4×18=9,
因此x﹣y=3或x﹣y=﹣3,
答:x﹣y的值为3或﹣3.
27.解:(1)方法一:两个正方形的面积和,即a2+b2,
方法二:边长为a+b的正方形的面积减去两个空白的长方形的面积,即(a+b)2﹣2ab,
因此有a2+b2=(a+b)2﹣2ab,
(2)图②阴影部分的面积是两个边长分别为a、b的正方形的面积和减去两个直角三角形的面积,
即a2+b2﹣a×a﹣(a+b)×b=a2+b2﹣ab=(a2+b2﹣ab)
=[(a+b)2﹣3ab],
当a+b=ab=9时,原式=×(81﹣27)=27,
答:阴影部分的面积为27.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
