2012高考数学模拟题(有答案)
文档属性
| 名称 | 2012高考数学模拟题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-19 00:00:00 | ||
图片预览




文档简介
2012年数学高考模拟题(理科)
时间:120分 满分;150分
选择题(12×5分,每题5分)。在每小题的四个选项中,只有一个符合要求。)
1. 已知集合,
则集合中的元素个数为 ( )
A.2个 B.1个 C.0个 D.无穷多个
2.过点且垂直于直线的直线方程为
A. B.
C. D.
3.已知,则的值等于 ( )
A. B. C. D.
4.若是真命题,是假命题,则
(A)是真命题 (B)是假命题
(C)是真命题 (D)是真命题
5. 4.设为奇函数,对任意R,均有,若,则等于( )
A.3 B. C.4 D.-4
6. 若,的最小值是( )
A B C -1 D
7. 连续抛掷一枚硬币3次,则至少有一次正面向上的概率是( )
A. B.
C. D.
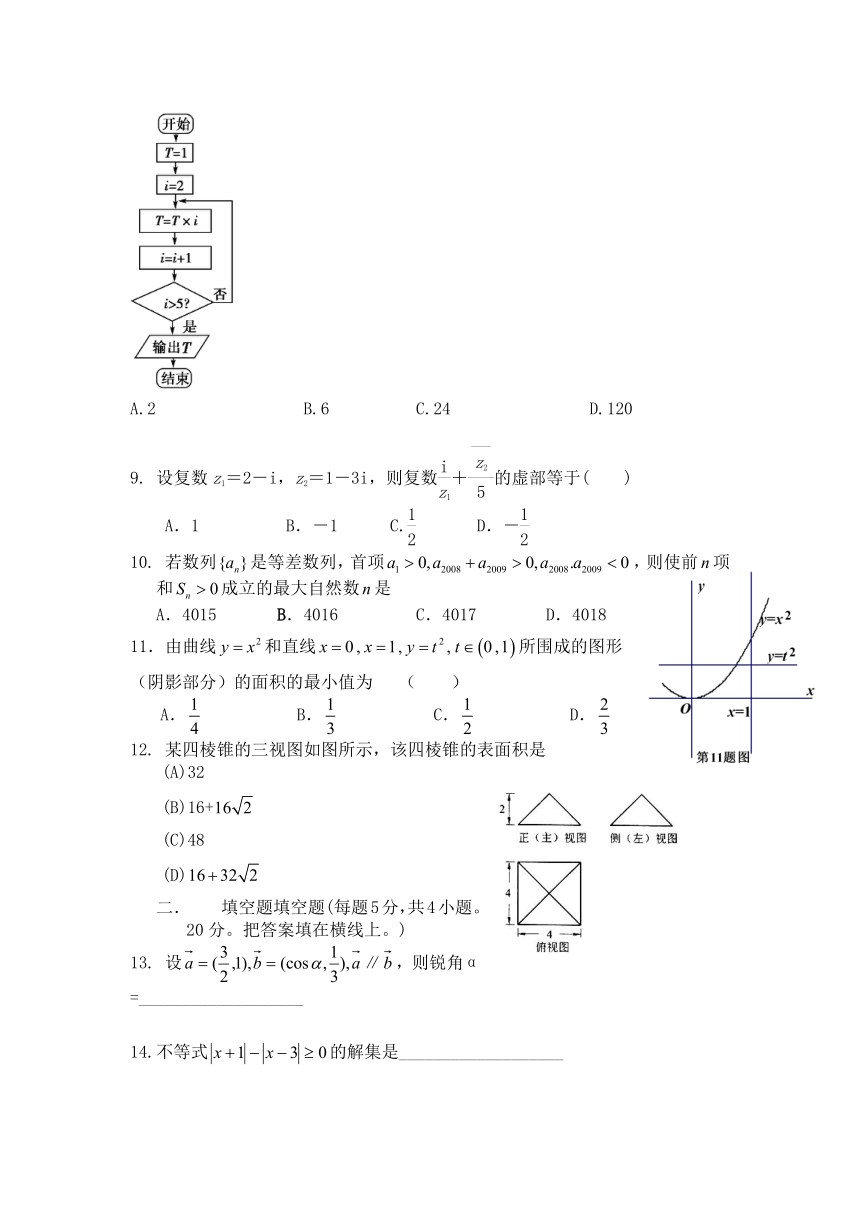
8.下图是一个算法的程序框图,输出结果是( )
A.2 B.6 C.24 D.120
9. 设复数z1=2-i,z2=1-3i,则复数+的虚部等于( )
A.1 B.-1 C. D.-
10. 若数列是等差数列,首项,则使前项
和成立的最大自然数是
A.4015 B.4016 C.4017 D.4018
11.由曲线和直线所围成的图形
(阴影部分)的面积的最小值为 ( )
A. B. C. D.
12. 某四棱锥的三视图如图所示,该四棱锥的表面积是
(A)32
(B)16+
(C)48
(D)
填空题填空题(每题5分,共4小题。20分。把答案填在横线上。)
13. 设∥,则锐角α=___________________
14.不等式的解集是___________________
15. 函数图象如右图所示,则函数的
单调递减区间为 .
16.设分别是椭圆的左右焦点,点在椭圆上,若则点A的坐标是 .
三.解答题。(共6小题,70分。解答时写出文字说明,或演算步骤。)
17.(本小题满分10分)直线经过点,且与两坐标轴的正半轴围成的三角形面积为4,求直线的方程.
18.(本小题满分12分)
已知实数列等比数列,其中,且成等差数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)数列的前项和记为,证明:<128…).
19.(本小题满分12分)
在中,内角对边的边长分别是,已知,.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
20. (本小题满分12分)如图,在四棱锥中,平面,底面是菱形,.
(Ⅰ)求证:平面
(Ⅱ)若求与所成角的余弦值;
(Ⅲ)当平面与平面垂直时,求的长.
21.(本小题满分12分)
(Ⅰ)已知函数,,求函数的最大值;
(Ⅱ)设…,均为正数,证明:
(1)若……,则;
(2)若…=1,则
22.( 本小题满分12分)已知抛物线C:x=2py(p>0)的焦点为F,A B是抛物线C上异于坐标原点O的不同两点,抛物线C在A B处的切线分别为l l,且l⊥l,l与l相交于点D.
(1)求点D的纵坐标;
(2)证明:A B F三点共线.
参考答案
1. A
2.D
3. C
4. D
5. B
6. A
7. B
8.D
9. A
10. B
11.A
12. B
13.
14.
15.
16.(0,)
17.解:设方程,则由题意:
当时,由得a=2,b=4,此时方程为
18.解:(Ⅰ)设等比数列的公比为,
由,得,从而,,.
因为成等差数列,所以,
即,.
所以.故
(Ⅱ).
19.解:(Ⅰ)由余弦定理得,,
又因为的面积等于,
所以,得.
联立方程组解得,.
(Ⅱ)由题意得,
当时,;
当时, 得,由正弦定理得,
联立方程组解得,.
所以的面积.
20.
证明:(Ⅰ)因为四边形ABCD是菱形,
所以AC⊥BD.
又因为PA⊥平面ABCD.
所以PA⊥BD.
所以BD⊥平面PAC.
(Ⅱ)设AC∩BD=O.
因为∠BAD=60°,PA=PB=2,
所以BO=1,AO=CO=.
如图,以O为坐标原点,建立空间直角坐标系O—xyz,则
P(0,—,2),A(0,—,0),B(1,0,0),C(0,,0).
所以
设PB与AC所成角为,则
.
(Ⅲ)由(Ⅱ)知
设P(0,-,t)(t>0),
则
设平面PBC的法向量,
则
所以
令则
所以
同理,平面PDC的法向量
因为平面PCB⊥平面PDC,
所以=0,即
解得
所以PA=
21.解:(I)的定义域为,令
当在(0,1)内是增函数;
当时,内是减函数;
故函数处取得最大值
(II)(1)由(I)知,当时,
有
,从而有,
得,
求和得
即
(2)①先证
令
则于是
由(1)得,即
②再证
记,
则,
于是由(1)得
即
综合①②,(2)得证。
22.
时间:120分 满分;150分
选择题(12×5分,每题5分)。在每小题的四个选项中,只有一个符合要求。)
1. 已知集合,
则集合中的元素个数为 ( )
A.2个 B.1个 C.0个 D.无穷多个
2.过点且垂直于直线的直线方程为
A. B.
C. D.
3.已知,则的值等于 ( )
A. B. C. D.
4.若是真命题,是假命题,则
(A)是真命题 (B)是假命题
(C)是真命题 (D)是真命题
5. 4.设为奇函数,对任意R,均有,若,则等于( )
A.3 B. C.4 D.-4
6. 若,的最小值是( )
A B C -1 D
7. 连续抛掷一枚硬币3次,则至少有一次正面向上的概率是( )
A. B.
C. D.
8.下图是一个算法的程序框图,输出结果是( )
A.2 B.6 C.24 D.120
9. 设复数z1=2-i,z2=1-3i,则复数+的虚部等于( )
A.1 B.-1 C. D.-
10. 若数列是等差数列,首项,则使前项
和成立的最大自然数是
A.4015 B.4016 C.4017 D.4018
11.由曲线和直线所围成的图形
(阴影部分)的面积的最小值为 ( )
A. B. C. D.
12. 某四棱锥的三视图如图所示,该四棱锥的表面积是
(A)32
(B)16+
(C)48
(D)
填空题填空题(每题5分,共4小题。20分。把答案填在横线上。)
13. 设∥,则锐角α=___________________
14.不等式的解集是___________________
15. 函数图象如右图所示,则函数的
单调递减区间为 .
16.设分别是椭圆的左右焦点,点在椭圆上,若则点A的坐标是 .
三.解答题。(共6小题,70分。解答时写出文字说明,或演算步骤。)
17.(本小题满分10分)直线经过点,且与两坐标轴的正半轴围成的三角形面积为4,求直线的方程.
18.(本小题满分12分)
已知实数列等比数列,其中,且成等差数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)数列的前项和记为,证明:<128…).
19.(本小题满分12分)
在中,内角对边的边长分别是,已知,.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
20. (本小题满分12分)如图,在四棱锥中,平面,底面是菱形,.
(Ⅰ)求证:平面
(Ⅱ)若求与所成角的余弦值;
(Ⅲ)当平面与平面垂直时,求的长.
21.(本小题满分12分)
(Ⅰ)已知函数,,求函数的最大值;
(Ⅱ)设…,均为正数,证明:
(1)若……,则;
(2)若…=1,则
22.( 本小题满分12分)已知抛物线C:x=2py(p>0)的焦点为F,A B是抛物线C上异于坐标原点O的不同两点,抛物线C在A B处的切线分别为l l,且l⊥l,l与l相交于点D.
(1)求点D的纵坐标;
(2)证明:A B F三点共线.
参考答案
1. A
2.D
3. C
4. D
5. B
6. A
7. B
8.D
9. A
10. B
11.A
12. B
13.
14.
15.
16.(0,)
17.解:设方程,则由题意:
当时,由得a=2,b=4,此时方程为
18.解:(Ⅰ)设等比数列的公比为,
由,得,从而,,.
因为成等差数列,所以,
即,.
所以.故
(Ⅱ).
19.解:(Ⅰ)由余弦定理得,,
又因为的面积等于,
所以,得.
联立方程组解得,.
(Ⅱ)由题意得,
当时,;
当时, 得,由正弦定理得,
联立方程组解得,.
所以的面积.
20.
证明:(Ⅰ)因为四边形ABCD是菱形,
所以AC⊥BD.
又因为PA⊥平面ABCD.
所以PA⊥BD.
所以BD⊥平面PAC.
(Ⅱ)设AC∩BD=O.
因为∠BAD=60°,PA=PB=2,
所以BO=1,AO=CO=.
如图,以O为坐标原点,建立空间直角坐标系O—xyz,则
P(0,—,2),A(0,—,0),B(1,0,0),C(0,,0).
所以
设PB与AC所成角为,则
.
(Ⅲ)由(Ⅱ)知
设P(0,-,t)(t>0),
则
设平面PBC的法向量,
则
所以
令则
所以
同理,平面PDC的法向量
因为平面PCB⊥平面PDC,
所以=0,即
解得
所以PA=
21.解:(I)的定义域为,令
当在(0,1)内是增函数;
当时,内是减函数;
故函数处取得最大值
(II)(1)由(I)知,当时,
有
,从而有,
得,
求和得
即
(2)①先证
令
则于是
由(1)得,即
②再证
记,
则,
于是由(1)得
即
综合①②,(2)得证。
22.
