2020-2021学年湘教版(2012)初中数学八年级下册 2.1.1 多边形 多边形的内角和 课件(共15张ppt)
文档属性
| 名称 | 2020-2021学年湘教版(2012)初中数学八年级下册 2.1.1 多边形 多边形的内角和 课件(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 326.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 21:27:42 | ||
图片预览





文档简介
(共15张PPT)
第2章
四边形
2.1
多边形
第1课时
多边形的内角和
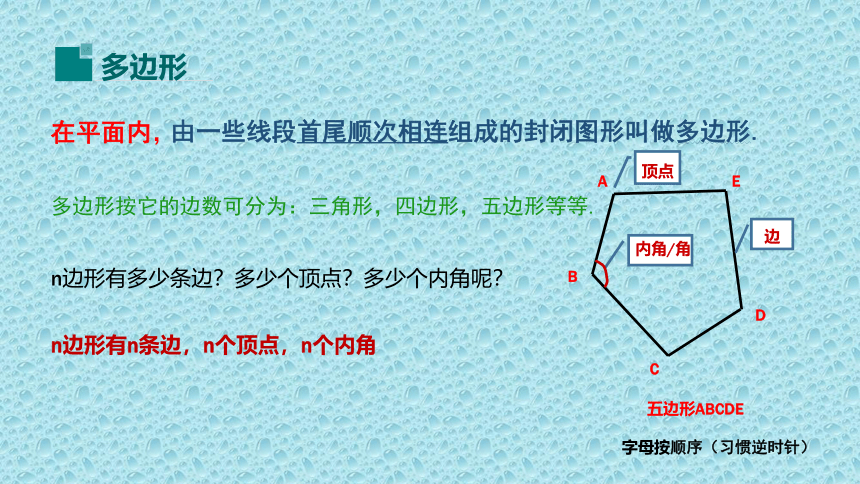
找一找:你能从图中找出一些由线段首尾相连所组成的图形吗?
由一些线段首尾顺次相连组成的封闭图形叫做多边形.
在平面内,
A
B
C
E
D
五边形ABCDE
n边形有多少条边?多少个顶点?多少个内角呢?
n边形有n条边,n个顶点,n个内角
多边形按它的边数可分为:三角形,四边形,五边形等等.
字母按顺序(习惯逆时针)
边
顶点
内角/角
多边形
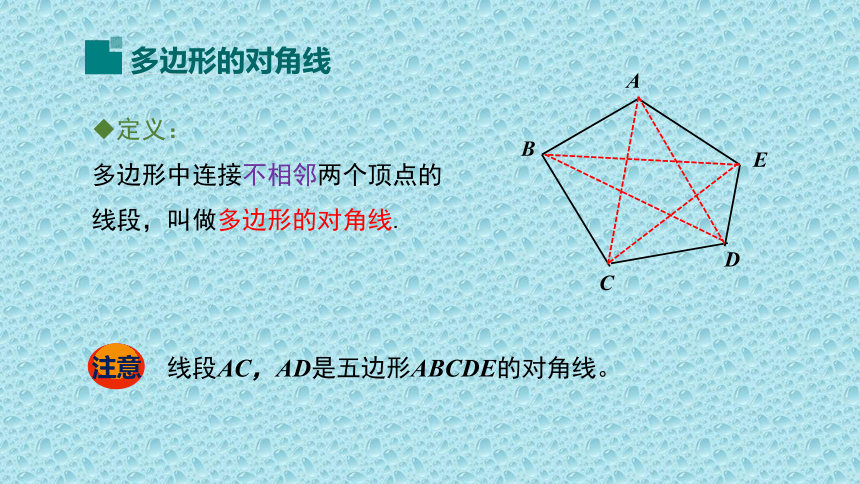
多边形的对角线
A
B
C
D
E
定义:
多边形中连接不相邻两个顶点的线段,叫做多边形的对角线.
线段AC,AD是五边形ABCDE的对角线。
注意
探究:请画出下列图形从某一顶点出发的对角线:
三角形
四边形
五边形
六边形
n边形
三角形
四边形
五边形
六边形
n边形
同一顶点对角线条数
对角线总条数
0
1
2
3
n-3
0
1
2
3
4
n-2
180?
2×180?
3×180?
4×180?
(
n
-2
)·180?
多边形的内角和
分割成的三角形个数
如果要探究多边形的内角和,分析上面的图,你会有什么启示?
探究2:过多边形中任一点作辅助线,构建三角形,探究多边形内角和公式
o
n边形的内角和
=n·180?-360?
=(
n
-2
)·180?
=n个三角形的内角和度数-中心圆周角度数
n边形的内角和等于(
n
-2
)·180?
1.九边形的内角和是多少?
2.一个多边形的内角和等于1980°,它是几边形?
解:(9-2)×180°=1260°
解:设这个多边形的边数为n,则
(n-2)×180°=1980°
解得:n=13
所以这是一个十三边形.
练一练
正多边形
三
定义:
在平面内,边相等、角也都相等的多边形叫作正多边形.
正三角形
正方形
正五边形
正六边形
想一想:下列多边形是正多边形吗?如不是,请说明为什么?
(四条边都相等)
(四个角都相等)
答:都不是,第一个图形不符合四个角都相等;第二个图形不符合各边都相等.
判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备.
注意
算一算:算出下列正多边形一个内角的度数
正十边形
正十二边形
例
如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
解析:根据五边形的内角和等于540°,由∠C,∠D,∠E的度数可求∠EAB+∠ABC的度数,再根据角平分线的定义可得∠PAB与∠PBA的角度和,进一步求得∠P的度数.
可运用
整体思想
解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°-100°-75°-135°=230°.
∵AP平分∠EAB,
∴∠PAB=
∠EAB,
同理可得∠ABP=
∠ABC,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°-∠PAB-∠PBA
=180°?
(∠EAB+∠ABC)=180°?
×230°=65°.
通过本节课的学习,你有何收获?
困惑?
温馨提醒?
课堂小结
2.若从一个多边形的一个顶点出发,最多可以引10条对角线,则这是
边形.
十三
3.过八边形的一个顶点画对角线,把这个八边形分割成
个三角形.
六
当堂练习
1.一个多边形的内角和不可能是(
)
A.1800°
B.540
°
C.720
°
D.810
°
D
一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
解:∵1800÷180=10,
∴原多边形边数为10+2=12.
∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1.
∴新多边形的边数可能是11,12,13,
∴新多边形的内角和可能是1620°,1800°,1980°.
拓展探究
第2章
四边形
2.1
多边形
第1课时
多边形的内角和
找一找:你能从图中找出一些由线段首尾相连所组成的图形吗?
由一些线段首尾顺次相连组成的封闭图形叫做多边形.
在平面内,
A
B
C
E
D
五边形ABCDE
n边形有多少条边?多少个顶点?多少个内角呢?
n边形有n条边,n个顶点,n个内角
多边形按它的边数可分为:三角形,四边形,五边形等等.
字母按顺序(习惯逆时针)
边
顶点
内角/角
多边形
多边形的对角线
A
B
C
D
E
定义:
多边形中连接不相邻两个顶点的线段,叫做多边形的对角线.
线段AC,AD是五边形ABCDE的对角线。
注意
探究:请画出下列图形从某一顶点出发的对角线:
三角形
四边形
五边形
六边形
n边形
三角形
四边形
五边形
六边形
n边形
同一顶点对角线条数
对角线总条数
0
1
2
3
n-3
0
1
2
3
4
n-2
180?
2×180?
3×180?
4×180?
(
n
-2
)·180?
多边形的内角和
分割成的三角形个数
如果要探究多边形的内角和,分析上面的图,你会有什么启示?
探究2:过多边形中任一点作辅助线,构建三角形,探究多边形内角和公式
o
n边形的内角和
=n·180?-360?
=(
n
-2
)·180?
=n个三角形的内角和度数-中心圆周角度数
n边形的内角和等于(
n
-2
)·180?
1.九边形的内角和是多少?
2.一个多边形的内角和等于1980°,它是几边形?
解:(9-2)×180°=1260°
解:设这个多边形的边数为n,则
(n-2)×180°=1980°
解得:n=13
所以这是一个十三边形.
练一练
正多边形
三
定义:
在平面内,边相等、角也都相等的多边形叫作正多边形.
正三角形
正方形
正五边形
正六边形
想一想:下列多边形是正多边形吗?如不是,请说明为什么?
(四条边都相等)
(四个角都相等)
答:都不是,第一个图形不符合四个角都相等;第二个图形不符合各边都相等.
判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备.
注意
算一算:算出下列正多边形一个内角的度数
正十边形
正十二边形
例
如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
解析:根据五边形的内角和等于540°,由∠C,∠D,∠E的度数可求∠EAB+∠ABC的度数,再根据角平分线的定义可得∠PAB与∠PBA的角度和,进一步求得∠P的度数.
可运用
整体思想
解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°-100°-75°-135°=230°.
∵AP平分∠EAB,
∴∠PAB=
∠EAB,
同理可得∠ABP=
∠ABC,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°-∠PAB-∠PBA
=180°?
(∠EAB+∠ABC)=180°?
×230°=65°.
通过本节课的学习,你有何收获?
困惑?
温馨提醒?
课堂小结
2.若从一个多边形的一个顶点出发,最多可以引10条对角线,则这是
边形.
十三
3.过八边形的一个顶点画对角线,把这个八边形分割成
个三角形.
六
当堂练习
1.一个多边形的内角和不可能是(
)
A.1800°
B.540
°
C.720
°
D.810
°
D
一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
解:∵1800÷180=10,
∴原多边形边数为10+2=12.
∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1.
∴新多边形的边数可能是11,12,13,
∴新多边形的内角和可能是1620°,1800°,1980°.
拓展探究
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
