人教版数学八年级下册 第18章平行四边形单元同步提升专练(word解析版)
文档属性
| 名称 | 人教版数学八年级下册 第18章平行四边形单元同步提升专练(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 159.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 08:27:48 | ||
图片预览


文档简介
【平行四边形】单元同步提升专练
一.选择题
1.如图,菱形ABCD的对角线AC、BD相交于点O,∠ABD=30°,BC=4,则边AD与BC之间的距离为( )
A.2
B.2
C.
D.
2.?ABCD中,∠A:∠B:∠C:∠D的度数比可能是( )
A.1:1:2:3
B.1:2:1:2
C.1:1:2:2
D.1:2:2:1
3.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是( )
A.28
B.24
C.14
D.18
4.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
5.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,过点D作DF∥BE交AC于F,则EF的长等于( )
A.2
B.3
C.
D.
6.如图,四边形ABCD是菱形,E、F分别是BC、CD两边上的点,不能保证△ABE和△ADF一定全等的条件是( )
A.∠BAF=∠DAE
B.EC=FC
C.AE=AF
D.BE=DF
7.如图,四边形ABCD的两条对角线AC,BD交于点O,OA=OC,OB=OD.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD
B.AB=BC
C.AC=BD
D.∠BAC=∠DAC
8.如图,在Rt△ABC中,CD是斜边AB上的中线,DE⊥AC于点E,若DE=1,∠A=30°,则△ABC的面积为( )
A.
B.3
C.
D.
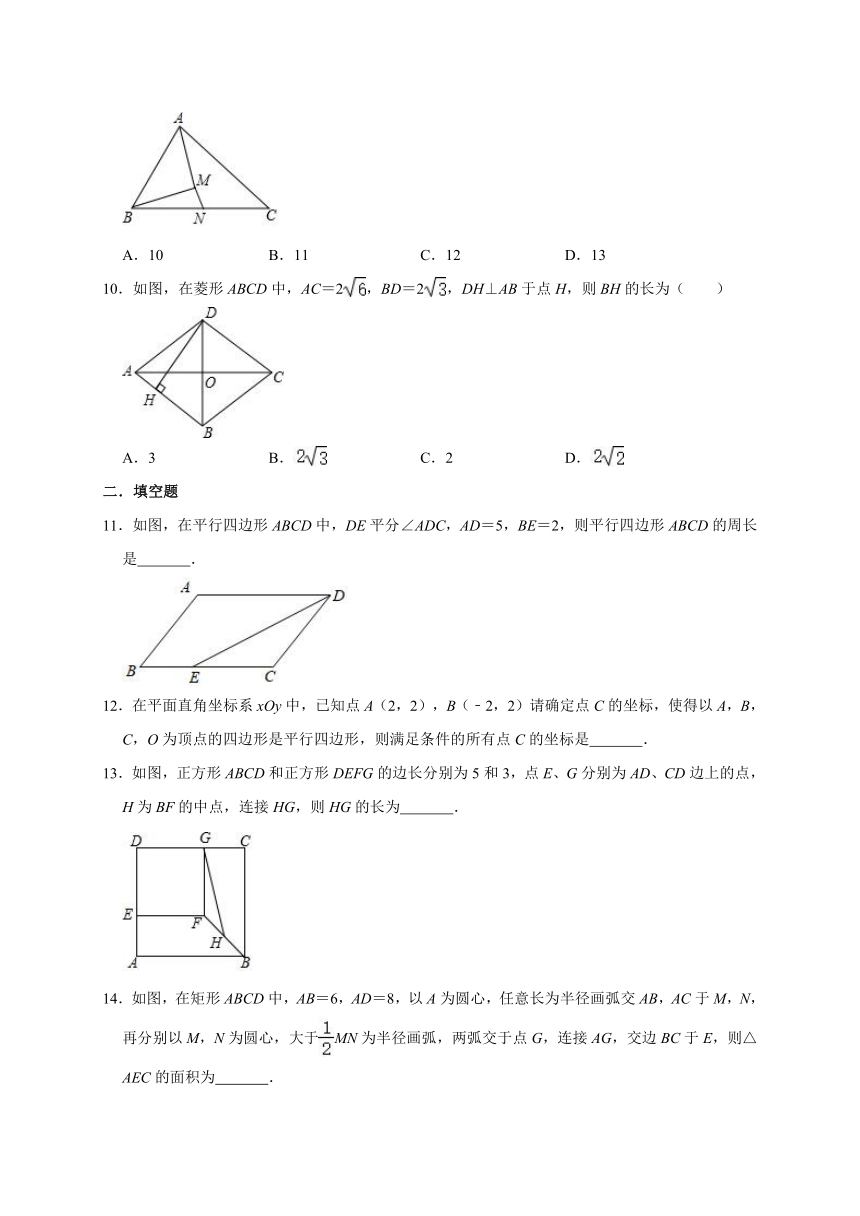
9.如图,△ABC中,N是BC边上的中点,AM平分∠BAC,BM⊥AM于点M,若AB=8,MN=2.则AC的长为( )
A.10
B.11
C.12
D.13
10.如图,在菱形ABCD中,AC=2,BD=2,DH⊥AB于点H,则BH的长为( )
A.3
B.
C.2
D.
二.填空题
11.如图,在平行四边形ABCD中,DE平分∠ADC,AD=5,BE=2,则平行四边形ABCD的周长是
.
12.在平面直角坐标系xOy中,已知点A(2,2),B(﹣2,2)请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是
.
13.如图,正方形ABCD和正方形DEFG的边长分别为5和3,点E、G分别为AD、CD边上的点,H为BF的中点,连接HG,则HG的长为
.
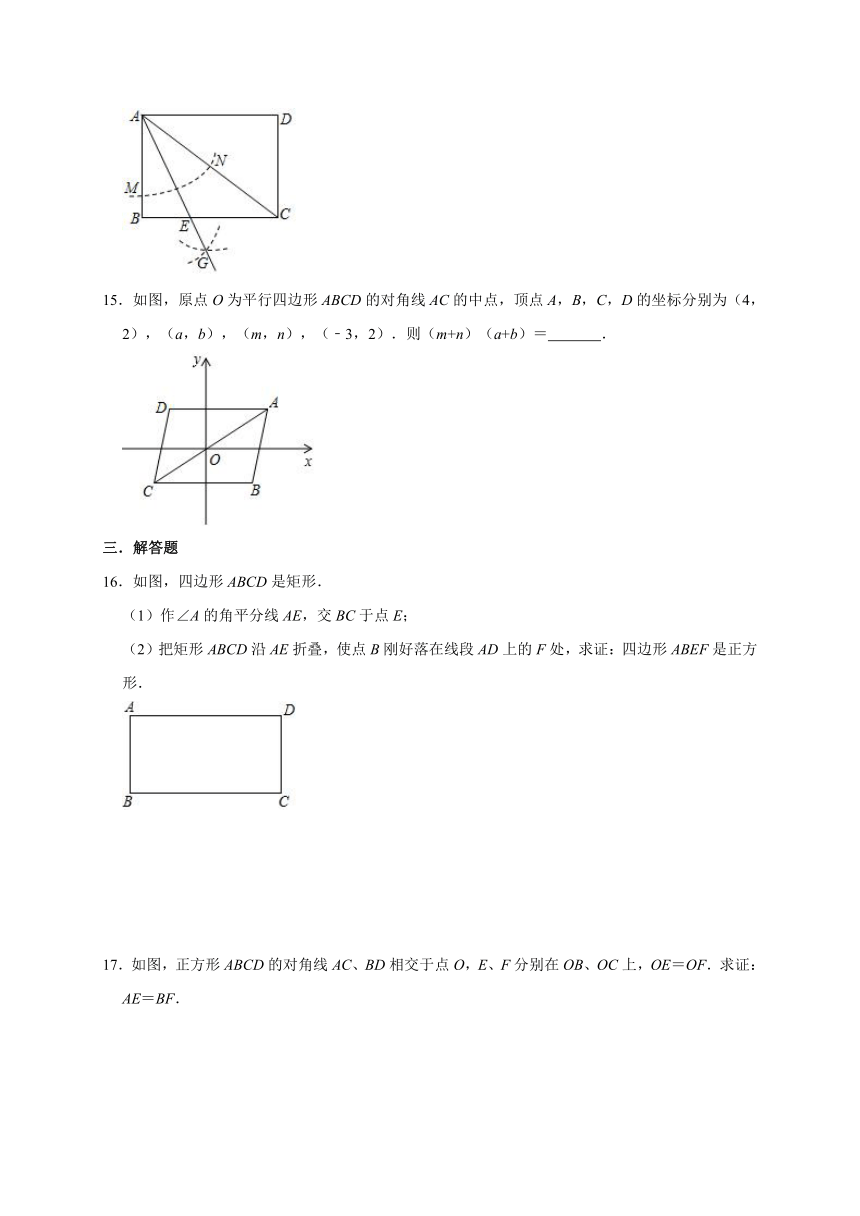
14.如图,在矩形ABCD中,AB=6,AD=8,以A为圆心,任意长为半径画弧交AB,AC于M,N,再分别以M,N为圆心,大于MN为半径画弧,两弧交于点G,连接AG,交边BC于E,则△AEC的面积为
.
15.如图,原点O为平行四边形ABCD的对角线AC的中点,顶点A,B,C,D的坐标分别为(4,2),(a,b),(m,n),(﹣3,2).则(m+n)(a+b)=
.
三.解答题
16.如图,四边形ABCD是矩形.
(1)作∠A的角平分线AE,交BC于点E;
(2)把矩形ABCD沿AE折叠,使点B刚好落在线段AD上的F处,求证:四边形ABEF是正方形.
17.如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.
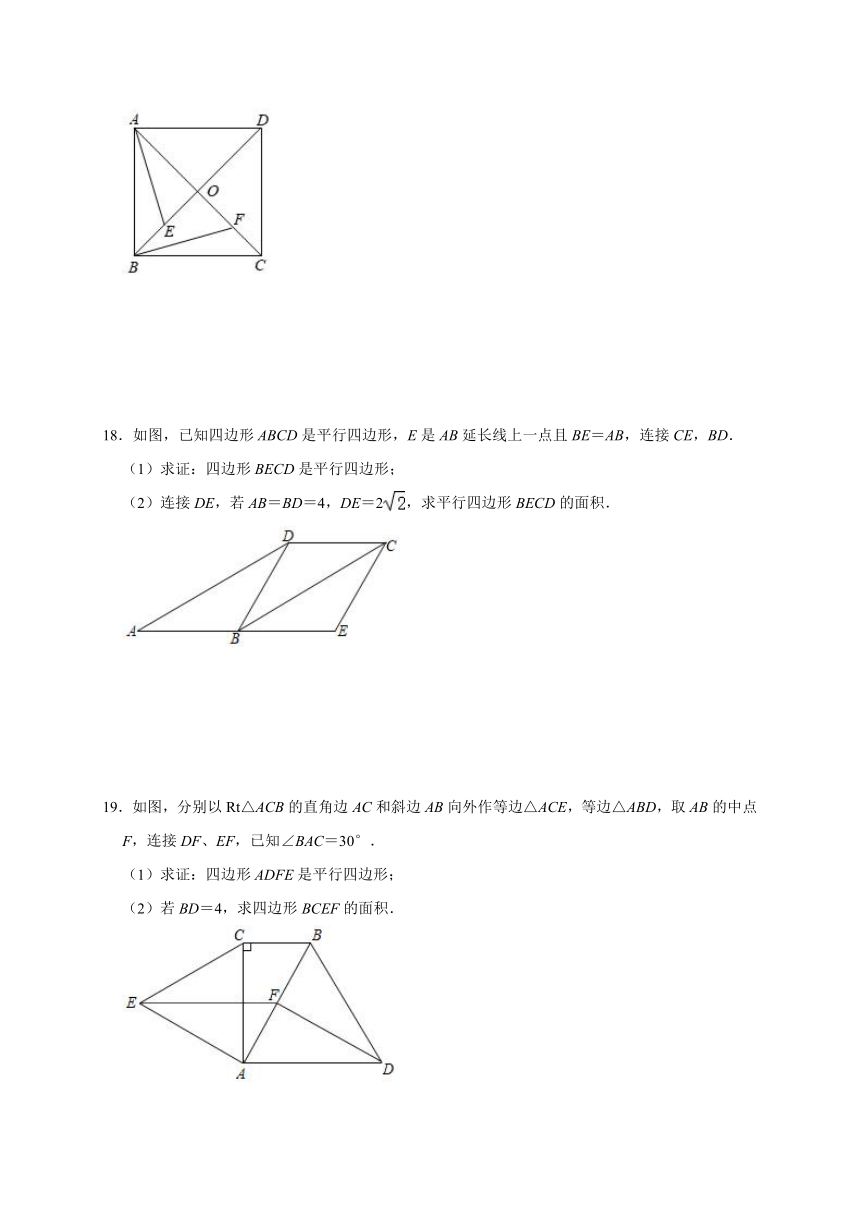
18.如图,已知四边形ABCD是平行四边形,E是AB延长线上一点且BE=AB,连接CE,BD.
(1)求证:四边形BECD是平行四边形;
(2)连接DE,若AB=BD=4,DE=2,求平行四边形BECD的面积.
19.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB的中点F,连接DF、EF,已知∠BAC=30°.
(1)求证:四边形ADFE是平行四边形;
(2)若BD=4,求四边形BCEF的面积.
20.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF,AE.
(1)求证:四边形BDCF为菱形;
(2)若四边形BDCF的面积为24,tan∠EAC=,求CF的长.
参考答案
一.选择题
1.解:过点A作AE⊥BC,
∵四边形ABCD为菱形,
∴∠ABD=∠CBD,AB=BC,
∵∠ABD=30°,
∴∠ABC=60°,
∴∠BAE=30°,
∴BE=2,AE=2.
即边AD与BC之间的距离为2.
故选:B.
2.解:根据平行四边形的两组对角分别相等,可知B正确.
故选:B.
3.解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,DE∥BC,
∵DE∥BC,EF∥DC,
∴四边形CDEF为平行四边形,
∴CD+DE=×10=5,
在Rt△ACB中,D是AB的中点,
∴AB=2CD,
∴AB+BC=2CD+2DE=2(CD+DE)=10,
∵AC=4,
∴△ABC的周长=AB+BC+AC=14(cm),
故选:C.
4.解:A、∵四边形ABCD是平行四边形,AC=BD,
∴四边形ABCD是矩形,正确,故本选项错误;
B、四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,正确,故本选项错误;
C、∵四边形ABCD是平行四边形,AC平分∠BAD,
∴四边形ABCD是菱形,正确,故本选项错误;
D、四边形ABCD是平行四边形,∠DAB=90°,
∴四边形ABCD是矩形,错误,故本选项正确;
故选:D.
5.解:∵DF∥BE,AD是△ABC的中线,
∴DF=BE=2,
∵AD⊥BE,DF=2,AD=4,
∴AF=,
∴EF=,
故选:C.
6.解:A.∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵∠BAF=∠DAE,
∴∠BAE=∠CAF,
∴△ABE≌△ADF(AAS),
故选项A不符合题意;
B..∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,BC=BD,
∵EC=FC,
∴BE=DF,
∴△ABE≌△ADF(SAS),
故选项B不符合题意;
C..∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵AE=AF,
∴△ABE和△ADF只满足两边和一边的对角相等,两个三角形不一定全等,
故选项C符合题意;
D..∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
又∵BE=DE,
∴△ABE≌△ADF(SAS),
故选项D不符合题意.
故选:C.
7.解:∵四边形ABCD中,OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
当AB=BC或AC⊥BD时,均可判定四边形ABCD是菱形;
当AC=BD时,可判定四边形ABCD是矩形;
当∠BAC=∠DAC时,
由AD∥BC得:∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴四边形ABCD是菱形;
故选:C.
8.解:∵在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD=BD=AB
∵DE⊥AC,∠A=30°,DE=1
∴AD=2
∴AB=4
∴BC=2
∴AC=2.
∴△ABC的面积为2.
故选:D.
9.解:延长BM交AC于D,如图所示:
∵BM⊥AM于点M,
∴∠AMB=∠AMD=90°,
∵AM平分∠BAC,
∴∠BAM=∠DAM,
在△BAM和△DAM中,
,
∴△BAM≌△DAM(ASA).
∴AD=AB=8,BM=MD,
∵N是BC边上的中点,
∴MN为△BCD的中位线,
∴DC=2MN=4,
∴AC=AD+DC=8+4=12.
故选:C.
10.解:在菱形ABCD中,AC=2,BD=2,
∴AO=CO=AC=,BO=DO=BD=,
∴AB===3,
∵DH×AB=AC×BD,
∴DH==2,
∴BH===2,
故选:C.
二.填空题
11.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DEC=∠CDE,
∴CD=CE=BC﹣BE=AD﹣BE=5﹣2=3,
∴平行四边形ABCD的周长是2AD+2DC=10+6=16.
故答案为:16.
12.解:如图,①当AB为该平行四边形的边时,AB=OC,
∵点A(2,2),B(﹣2,2),O(0,0)
∴点C坐标(﹣4,0)或(4,0)
②当AB为该平行四边形的对角线时,C(0,4).
故答案是:(﹣4,0)或(4,0)或(0,4).
13.解:延长GF交AB于P,过H作MN⊥CD于M,交AB于N,
∵四边形ABCD是正方形,
∴AB∥CD,BC⊥CD,
∴MN⊥AB,
∵四边形DEFG是正方形,
∴FG⊥CD,
∴FG∥HM∥BC,
∵H是BF的中点,
∴PN=BN=CM=GM=CG==1,
∴HN是△BFP的中位线,
∴HN=FP=1,
∴MH=5﹣1=4,
Rt△GHM中,由勾股定理得:GH==.
故答案为:.
14.解:作EF⊥AC于F,如图:
由题意得:AE平分∠BAC,
∵四边形ABCD是矩形,
∴∠B=90°,BC=AD=8,
∴AC===10,
EB⊥AB,
∵AE平分∠BAC,
∴EF=EB,
在Rt△AEF和Rt△AEB中,,
∴Rt△AEF≌Rt△AEB(HL),
∴AF=AB=6,
∴CF=AC﹣AF=4,
设EF=EB=x,则CE=8﹣x,
在Rt△CEF中,由勾股定理得:x2+42=(8﹣x)2,
解得:x=3,
∴EF=3,
∴△AEC的面积=AC×EF=×10×3=15;
故答案为:15.
15.解:
∵点O为平行四边形ABCD的对角线AC的中点,顶点A的坐标为(4,2),
∴顶点C的坐标为(﹣4,﹣2),
∴m=﹣4,n=﹣2,
∵顶点D的坐标为(﹣3,2),
∴顶点B的坐标为(3,﹣2),
∴a=3,b=﹣2,
∴(m+n)(a+b)=﹣6×1=﹣6,
故答案为:﹣6.
三.解答题
16.解:(1)如图,AE为所作;
(2)正方形的性质和翻折变换的性质可知,∠B=∠BAF=∠AFE=90°,
∴四边形ABEF是矩形,
由翻折变换的性质可知,AB=AF,
∴四边形ABEF是正方形.
17.证明:∵四边形ABCD为正方形,
∴OA=OB,AC⊥BD,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS)
∴AE=BF.
18.(1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AE,
∵AB=BE,
∴CD=BE,CD∥BE,
∴四边形BECD是平行四边形;
(2)解:过D作DH⊥AE于H,
∵AB=BD=4,
∴BE=AB=4,
∴BD2﹣BH2=DE2﹣EH2=DH2,
∴42﹣BH2=(2)2﹣(4﹣BH)2,
∴BH=3,
∴DH===,
∴平行四边形BECD的面积=BE?DH=4×=4.
19.(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABD是等边三角形,F是AB的中点,
∴AD=AB=BD,AB=2AF,DF⊥AB,
∴AF=BC,
在Rt△AFD和Rt△BCA中,
,
∴Rt△AFD≌Rt△BCA(HL),
∴DF=AC,
∵△ACE是等边三角形,
∴∠EAC=60°,AC=AE,
∴∠EAB=∠EAC+∠BAC=90°,
∴DF=AE,
又∵DF⊥AB,
∴DF∥AE,
∴四边形ADFE是平行四边形;
(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC=AB=2,AC=BC=2,
∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.
20.(1)证明:DE⊥BC,∠ACB=90°,
∴∠BED=∠ACB,
∴DF∥AC,
∵CF∥AB,
∴四边形ADFC是平行四边形,
∴AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,
∵BD∥CF,
∴四边形BDCF是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴DC=BD,
∴四边形BDCF是菱形;
(2)解:∵tan∠EAC==,
∴设CE=2x,AC=3x,
∵四边形BDCF是菱形,
∴BE=CE=2x,
∴BC=4x,
∵四边形ADFC是平行四边形,
∴DF=AC=3x,
∵四边形BDCF的面积为24,
∴=24,
∴,
解得:x=2(负数舍去),
∴CE=4,DF=6,
∴DE=EF=×6=3,
∵DE⊥BC,
∴∠CEF=90°,
∴由勾股定理得:CF===5.
一.选择题
1.如图,菱形ABCD的对角线AC、BD相交于点O,∠ABD=30°,BC=4,则边AD与BC之间的距离为( )
A.2
B.2
C.
D.
2.?ABCD中,∠A:∠B:∠C:∠D的度数比可能是( )
A.1:1:2:3
B.1:2:1:2
C.1:1:2:2
D.1:2:2:1
3.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是( )
A.28
B.24
C.14
D.18
4.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
5.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,过点D作DF∥BE交AC于F,则EF的长等于( )
A.2
B.3
C.
D.
6.如图,四边形ABCD是菱形,E、F分别是BC、CD两边上的点,不能保证△ABE和△ADF一定全等的条件是( )
A.∠BAF=∠DAE
B.EC=FC
C.AE=AF
D.BE=DF
7.如图,四边形ABCD的两条对角线AC,BD交于点O,OA=OC,OB=OD.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD
B.AB=BC
C.AC=BD
D.∠BAC=∠DAC
8.如图,在Rt△ABC中,CD是斜边AB上的中线,DE⊥AC于点E,若DE=1,∠A=30°,则△ABC的面积为( )
A.
B.3
C.
D.
9.如图,△ABC中,N是BC边上的中点,AM平分∠BAC,BM⊥AM于点M,若AB=8,MN=2.则AC的长为( )
A.10
B.11
C.12
D.13
10.如图,在菱形ABCD中,AC=2,BD=2,DH⊥AB于点H,则BH的长为( )
A.3
B.
C.2
D.
二.填空题
11.如图,在平行四边形ABCD中,DE平分∠ADC,AD=5,BE=2,则平行四边形ABCD的周长是
.
12.在平面直角坐标系xOy中,已知点A(2,2),B(﹣2,2)请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是
.
13.如图,正方形ABCD和正方形DEFG的边长分别为5和3,点E、G分别为AD、CD边上的点,H为BF的中点,连接HG,则HG的长为
.
14.如图,在矩形ABCD中,AB=6,AD=8,以A为圆心,任意长为半径画弧交AB,AC于M,N,再分别以M,N为圆心,大于MN为半径画弧,两弧交于点G,连接AG,交边BC于E,则△AEC的面积为
.
15.如图,原点O为平行四边形ABCD的对角线AC的中点,顶点A,B,C,D的坐标分别为(4,2),(a,b),(m,n),(﹣3,2).则(m+n)(a+b)=
.
三.解答题
16.如图,四边形ABCD是矩形.
(1)作∠A的角平分线AE,交BC于点E;
(2)把矩形ABCD沿AE折叠,使点B刚好落在线段AD上的F处,求证:四边形ABEF是正方形.
17.如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.
18.如图,已知四边形ABCD是平行四边形,E是AB延长线上一点且BE=AB,连接CE,BD.
(1)求证:四边形BECD是平行四边形;
(2)连接DE,若AB=BD=4,DE=2,求平行四边形BECD的面积.
19.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB的中点F,连接DF、EF,已知∠BAC=30°.
(1)求证:四边形ADFE是平行四边形;
(2)若BD=4,求四边形BCEF的面积.
20.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF,AE.
(1)求证:四边形BDCF为菱形;
(2)若四边形BDCF的面积为24,tan∠EAC=,求CF的长.
参考答案
一.选择题
1.解:过点A作AE⊥BC,
∵四边形ABCD为菱形,
∴∠ABD=∠CBD,AB=BC,
∵∠ABD=30°,
∴∠ABC=60°,
∴∠BAE=30°,
∴BE=2,AE=2.
即边AD与BC之间的距离为2.
故选:B.
2.解:根据平行四边形的两组对角分别相等,可知B正确.
故选:B.
3.解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,DE∥BC,
∵DE∥BC,EF∥DC,
∴四边形CDEF为平行四边形,
∴CD+DE=×10=5,
在Rt△ACB中,D是AB的中点,
∴AB=2CD,
∴AB+BC=2CD+2DE=2(CD+DE)=10,
∵AC=4,
∴△ABC的周长=AB+BC+AC=14(cm),
故选:C.
4.解:A、∵四边形ABCD是平行四边形,AC=BD,
∴四边形ABCD是矩形,正确,故本选项错误;
B、四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,正确,故本选项错误;
C、∵四边形ABCD是平行四边形,AC平分∠BAD,
∴四边形ABCD是菱形,正确,故本选项错误;
D、四边形ABCD是平行四边形,∠DAB=90°,
∴四边形ABCD是矩形,错误,故本选项正确;
故选:D.
5.解:∵DF∥BE,AD是△ABC的中线,
∴DF=BE=2,
∵AD⊥BE,DF=2,AD=4,
∴AF=,
∴EF=,
故选:C.
6.解:A.∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵∠BAF=∠DAE,
∴∠BAE=∠CAF,
∴△ABE≌△ADF(AAS),
故选项A不符合题意;
B..∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,BC=BD,
∵EC=FC,
∴BE=DF,
∴△ABE≌△ADF(SAS),
故选项B不符合题意;
C..∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵AE=AF,
∴△ABE和△ADF只满足两边和一边的对角相等,两个三角形不一定全等,
故选项C符合题意;
D..∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
又∵BE=DE,
∴△ABE≌△ADF(SAS),
故选项D不符合题意.
故选:C.
7.解:∵四边形ABCD中,OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
当AB=BC或AC⊥BD时,均可判定四边形ABCD是菱形;
当AC=BD时,可判定四边形ABCD是矩形;
当∠BAC=∠DAC时,
由AD∥BC得:∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴四边形ABCD是菱形;
故选:C.
8.解:∵在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD=BD=AB
∵DE⊥AC,∠A=30°,DE=1
∴AD=2
∴AB=4
∴BC=2
∴AC=2.
∴△ABC的面积为2.
故选:D.
9.解:延长BM交AC于D,如图所示:
∵BM⊥AM于点M,
∴∠AMB=∠AMD=90°,
∵AM平分∠BAC,
∴∠BAM=∠DAM,
在△BAM和△DAM中,
,
∴△BAM≌△DAM(ASA).
∴AD=AB=8,BM=MD,
∵N是BC边上的中点,
∴MN为△BCD的中位线,
∴DC=2MN=4,
∴AC=AD+DC=8+4=12.
故选:C.
10.解:在菱形ABCD中,AC=2,BD=2,
∴AO=CO=AC=,BO=DO=BD=,
∴AB===3,
∵DH×AB=AC×BD,
∴DH==2,
∴BH===2,
故选:C.
二.填空题
11.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DEC=∠CDE,
∴CD=CE=BC﹣BE=AD﹣BE=5﹣2=3,
∴平行四边形ABCD的周长是2AD+2DC=10+6=16.
故答案为:16.
12.解:如图,①当AB为该平行四边形的边时,AB=OC,
∵点A(2,2),B(﹣2,2),O(0,0)
∴点C坐标(﹣4,0)或(4,0)
②当AB为该平行四边形的对角线时,C(0,4).
故答案是:(﹣4,0)或(4,0)或(0,4).
13.解:延长GF交AB于P,过H作MN⊥CD于M,交AB于N,
∵四边形ABCD是正方形,
∴AB∥CD,BC⊥CD,
∴MN⊥AB,
∵四边形DEFG是正方形,
∴FG⊥CD,
∴FG∥HM∥BC,
∵H是BF的中点,
∴PN=BN=CM=GM=CG==1,
∴HN是△BFP的中位线,
∴HN=FP=1,
∴MH=5﹣1=4,
Rt△GHM中,由勾股定理得:GH==.
故答案为:.
14.解:作EF⊥AC于F,如图:
由题意得:AE平分∠BAC,
∵四边形ABCD是矩形,
∴∠B=90°,BC=AD=8,
∴AC===10,
EB⊥AB,
∵AE平分∠BAC,
∴EF=EB,
在Rt△AEF和Rt△AEB中,,
∴Rt△AEF≌Rt△AEB(HL),
∴AF=AB=6,
∴CF=AC﹣AF=4,
设EF=EB=x,则CE=8﹣x,
在Rt△CEF中,由勾股定理得:x2+42=(8﹣x)2,
解得:x=3,
∴EF=3,
∴△AEC的面积=AC×EF=×10×3=15;
故答案为:15.
15.解:
∵点O为平行四边形ABCD的对角线AC的中点,顶点A的坐标为(4,2),
∴顶点C的坐标为(﹣4,﹣2),
∴m=﹣4,n=﹣2,
∵顶点D的坐标为(﹣3,2),
∴顶点B的坐标为(3,﹣2),
∴a=3,b=﹣2,
∴(m+n)(a+b)=﹣6×1=﹣6,
故答案为:﹣6.
三.解答题
16.解:(1)如图,AE为所作;
(2)正方形的性质和翻折变换的性质可知,∠B=∠BAF=∠AFE=90°,
∴四边形ABEF是矩形,
由翻折变换的性质可知,AB=AF,
∴四边形ABEF是正方形.
17.证明:∵四边形ABCD为正方形,
∴OA=OB,AC⊥BD,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS)
∴AE=BF.
18.(1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AE,
∵AB=BE,
∴CD=BE,CD∥BE,
∴四边形BECD是平行四边形;
(2)解:过D作DH⊥AE于H,
∵AB=BD=4,
∴BE=AB=4,
∴BD2﹣BH2=DE2﹣EH2=DH2,
∴42﹣BH2=(2)2﹣(4﹣BH)2,
∴BH=3,
∴DH===,
∴平行四边形BECD的面积=BE?DH=4×=4.
19.(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABD是等边三角形,F是AB的中点,
∴AD=AB=BD,AB=2AF,DF⊥AB,
∴AF=BC,
在Rt△AFD和Rt△BCA中,
,
∴Rt△AFD≌Rt△BCA(HL),
∴DF=AC,
∵△ACE是等边三角形,
∴∠EAC=60°,AC=AE,
∴∠EAB=∠EAC+∠BAC=90°,
∴DF=AE,
又∵DF⊥AB,
∴DF∥AE,
∴四边形ADFE是平行四边形;
(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC=AB=2,AC=BC=2,
∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.
20.(1)证明:DE⊥BC,∠ACB=90°,
∴∠BED=∠ACB,
∴DF∥AC,
∵CF∥AB,
∴四边形ADFC是平行四边形,
∴AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,
∵BD∥CF,
∴四边形BDCF是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴DC=BD,
∴四边形BDCF是菱形;
(2)解:∵tan∠EAC==,
∴设CE=2x,AC=3x,
∵四边形BDCF是菱形,
∴BE=CE=2x,
∴BC=4x,
∵四边形ADFC是平行四边形,
∴DF=AC=3x,
∵四边形BDCF的面积为24,
∴=24,
∴,
解得:x=2(负数舍去),
∴CE=4,DF=6,
∴DE=EF=×6=3,
∵DE⊥BC,
∴∠CEF=90°,
∴由勾股定理得:CF===5.
