苏科版八年级数学下册 11.2 反比例函数的图象和性质强化提优试卷(word版含答案)
文档属性
| 名称 | 苏科版八年级数学下册 11.2 反比例函数的图象和性质强化提优试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 08:32:14 | ||
图片预览




文档简介
苏科版八年级数学下册《
11.2
反比例函数的图象和性质》强化提优试卷(1)
(时间:60分钟
满分:100分)
1.选择题(共16题;共32分)
1.已知反比例函数y=的图象过点A(1,-2),则k的值为(
)
A.
1
B.
2
C.
-2
D.
-1
2.已知点A(1,-3)关于x轴的对称点A′在反比例函数y=的图象上,则实数k的值为(
)
A.
3
B.
C.
-3
D.
-
3.若反比例函数y=的图象如图所示,则一次函数y=kx+b(k≠0)的图象可能是(
)
4.对于反比例函数y=-图象对称性的叙述错误的是(
)
A.关于原点对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
5.在平面直角坐标系xOy中,反比例函数y=的图象与y=的图象关于x轴对称,且过点A(m,3),则m的值是(
)
A.2
B.-2
C.1
D.-1
6.
若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在(
)
A.第一、二象限
B.第一、三象限
C.第二、三象限
D.第二、四象限
7.若点A(3,-4),B(-2,m)在同一个反比例函数的图象上,则m的值为(
)
A.6 B.-6 C.12 D.-12
8.如图,反比例函数y=(x<0)的图象经过点P,则k的值为(
)
A.-6
B.-5
C.6
D.5
第8题图
第9题图
第10题图
第11题图
9.如图,反比例函数y=的图象与经过原点的直线l相交于A,B两点,点A的坐标为(-2,1),那么点B的坐标为(
)
A.(-2,1)
B.(2,1)
C.(1,-2)
D.(2,-1)
10.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上.若AB=1,则k的值为(
)
A.
1
B.
C.
D.
2
11.如图,函数的图象经过斜边的中点,连结.如果那么的周长为(
)
A.
B.
C.
D.
12.双曲线的图象过点,,则的值是(
)
A.
B.
C.
D.
13.在平面直角坐标系中,点,,分别在三个不同的象限,若反比例函数的图象经过其中两点,则的值为(
)
A.
B.1
C.或1
D.不能确定
14.反比例的图象经过点(-1,3),则k的值为(
)
A.
B.
C.
D.
15.一次函数与反比例函数在同一坐标系中的图象可能是(
)
A.
B.
C.D.
16.函数与在同一平面直角坐标系中的图象不可能是(
)
A.B.C.D.
2.填空题(共14题;共28分)
17.若点(a,-2a)在反比例函数y=的图象上,则此反比例函数的图象在第_______象限.
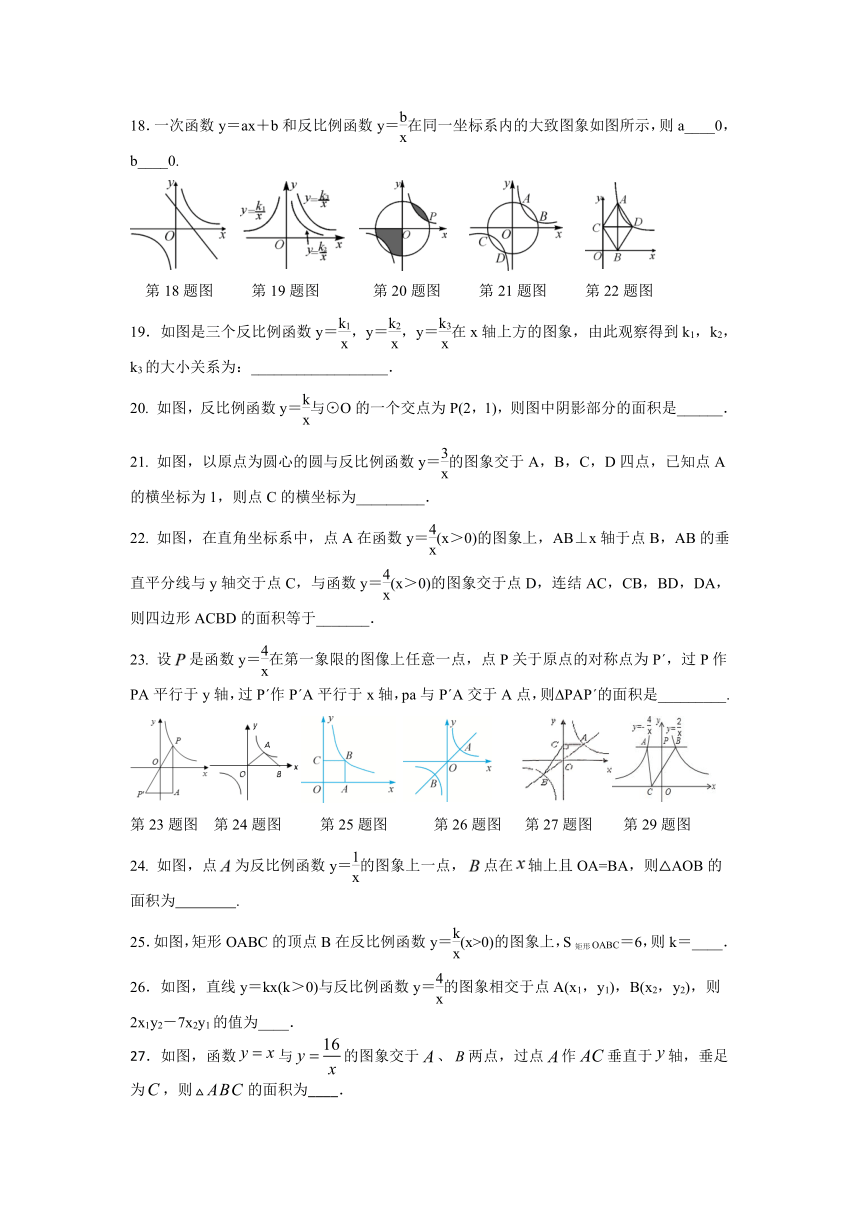
18.一次函数y=ax+b和反比例函数y=在同一坐标系内的大致图象如图所示,则a____0,b____0.
第18题图
第19题图
第20题图
第21题图
第22题图
19.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为:__________________.
20.
如图,反比例函数y=与⊙O的一个交点为P(2,1),则图中阴影部分的面积是______.
21.
如图,以原点为圆心的圆与反比例函数y=的图象交于A,B,C,D四点,已知点A的横坐标为1,则点C的横坐标为_________.
22.
如图,在直角坐标系中,点A在函数y=(x>0)的图象上,AB⊥x轴于点B,AB的垂直平分线与y轴交于点C,与函数y=(x>0)的图象交于点D,连结AC,CB,BD,DA,则四边形ACBD的面积等于_______.
23.
设是函数y=在第一象限的图像上任意一点,点P关于原点的对称点为P?,过P作PA平行于y轴,过P?作P?A平行于x轴,pa与P?A交于A点,则?PAP?的面积是_________.
第23题图
第24题图
第25题图
第26题图
第27题图
第29题图
24.
如图,点为反比例函数y=的图象上一点,点在轴上且OA=BA,则△AOB的面积为
.
25.如图,矩形OABC的顶点B在反比例函数y=(x>0)的图象上,S矩形OABC=6,则k=____.
26.如图,直线y=kx(k>0)与反比例函数y=的图象相交于点A(x1,y1),B(x2,y2),则2x1y2-7x2y1的值为____.
27.如图,函数与的图象交于、两点,过点作垂直于轴,垂足为,则的面积为____.
28.一个正比例函数的图象与反比例函数的图象交于,两点,则的值为_
___.
29.如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为_____.
3.解答题(共5小题
共40分)
30.(8分)如图,一次函数y=kx+b的图象与反比例函数y=-的图象相交于点A(-1,m),B(n,-1).
(1)求一次函数的表达式.
(2)求△AOB的面积.
31.(8分)如图,在?ABCD中,顶点A的坐标是(0,2),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是-4,?ABCD的面积是24.反比例函数y=的图象经过点B,D,求:
(1)反比例函数的表达式.
(2)AB所在直线的函数表达式.
32.(8分)如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,C分别在x轴、y轴的正半轴上,函数y=2x的图象与CB相交于点D,函数y=(k为常数,k≠0)的图象经过点D,与AB相交于点E,与函数y=2x的图象在第三象限相交于点F,连结AF,EF.
(1)求函数y=的表达式,并直接写出E,F两点的坐标.
(2)求△AEF的面积.
33.(8分)已知等腰三角形OAB(OA=OB)在平面直角坐标系中的位置如图所示,点A的坐标为(-3,3),点B的坐标为(-6,0).
(1)若△OAB关于y轴的轴对称图形是△OA′B′,请直接写出点A,B的对称点A′,B′的坐标.
(2)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=的图象上,求a的值.
(3)若将△OAB绕点O按逆时针方向旋转∠α(0°<∠α<90°).
①当∠α=30°时,点B恰好落在反比例函数y=的图象上,求k的值.
②点A,B能否同时落在①中的反比例函数的图象上?若能,请求出∠α的度数;若不能,请说明理由.
34.(8分)如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且B(4,3),反比例函数的图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及点E的坐标;
(2)求直线DE的解析式.
教师样卷
一.选择题(共16题;共32分)
1.已知反比例函数y=的图象过点A(1,-2),则k的值为(C)
A.
1
B.
2
C.
-2
D.
-1
2.已知点A(1,-3)关于x轴的对称点A′在反比例函数y=的图象上,则实数k的值为(A)
A.
3
B.
C.
-3
D.
-
3.若反比例函数y=的图象如图所示,则一次函数y=kx+b(k≠0)的图象可能是(D)
4.对于反比例函数y=-图象对称性的叙述错误的是(
D
)
A.关于原点对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
5.在平面直角坐标系xOy中,反比例函数y=的图象与y=的图象关于x轴对称,且过点A(m,3),则m的值是(
B
)
A.2
B.-2
C.1
D.-1
6.
若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在(
D
)
A.第一、二象限
B.第一、三象限
C.第二、三象限
D.第二、四象限
7.若点A(3,-4),B(-2,m)在同一个反比例函数的图象上,则m的值为(
A
)
A.6 B.-6 C.12 D.-12
8.如图,反比例函数y=(x<0)的图象经过点P,则k的值为(
A
)
A.-6
B.-5
C.6
D.5
第8题图
第9题图
第10题图
第11题图
9.如图,反比例函数y=的图象与经过原点的直线l相交于A,B两点,点A的坐标为(-2,1),那么点B的坐标为(
D
)
A.(-2,1)
B.(2,1)
C.(1,-2)
D.(2,-1)
10.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上.若AB=1,则k的值为(A)
A.
1
B.
C.
D.
2
11.如图,函数的图象经过斜边的中点,连结.如果那么的周长为(
D
)
A.
B.
C.
D.
解:如图1,过点C作CE⊥AO于E,∵点C是BO的中点∴AC=BC=CO=3,∴BO=6,∵CE⊥AO,AB⊥AO,∴AB∥CE,∴CE是的中位线,∴AB=2CE,AO=2EO,∵点在上,∴CE×EO=2,∴AB×AO=2
CE×2EO
=8,∵AB2+AO2=OB2=36,∴(AB+AO)2=36+16,∴AB+AO=
,∴△ABO的周长=AO+BO+AB=6+,故选:D.
12.双曲线的图象过点,,则的值是(
C
)
A.
B.
C.
D.
13.在平面直角坐标系中,点,,分别在三个不同的象限,若反比例函数的图象经过其中两点,则的值为(
A
)
A.
B.1
C.或1
D.不能确定
解:分三种情况:第一种情况,由,一个在第二象限,一个在第一象限,而反比例函数图象不能同时经过第一、二象限,故此情况无解;第二种情况,当反比函数经过A、C两点时,把由代入到得k=-2∴此时反比例函数的关系式为把代入得m=,
∴,其在第四象限和不在同一象限.∴m=;第三种情况,当反比函数经过B、C两点时,把代入到得k=6∴此时反比例函数的关系式为把代入得m=1,∴,其在第一象限和在同一象限.不合题意.故此情况下,无解.综上所述m=.故选:A.
14.反比例的图象经过点(-1,3),则k的值为(
C
)
A.
B.
C.
D.
15.一次函数与反比例函数在同一坐标系中的图象可能是(
D
)
A.
B.
C.D.
【详解】当时,则一次函数经过一、二、三象限,反比例函数经过一
、三象限,故排除A,C选项;当时,则一次函数经过二、三、四象限,反比例函数经过二、四象限,故排除B选项,故选择:D.
16.函数与在同一平面直角坐标系中的图象不可能是(
A
)
A.B.C.D.
二.
填空题(共14题;共28分)
17.若点(a,-2a)在反比例函数y=的图象上,则此反比例函数的图象在第二、四象限.
18.一次函数y=ax+b和反比例函数y=在同一坐标系内的大致图象如图所示,则a__<__0,b__>__0.
第18题图
第19题图
第20题图
第21题图
第22题图
19.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为:____k3>k2>k1_______________.
20.
如图,反比例函数y=与⊙O的一个交点为P(2,1),则图中阴影部分的面积是___π___.
21.
如图,以原点为圆心的圆与反比例函数y=的图象交于A,B,C,D四点,已知点A的横坐标为1,则点C的横坐标为___-3______.
22.
如图,在直角坐标系中,点A在函数y=(x>0)的图象上,AB⊥x轴于点B,AB的垂直平分线与y轴交于点C,与函数y=(x>0)的图象交于点D,连结AC,CB,BD,DA,则四边形ACBD的面积等于___4____.
23.
设是函数y=在第一象限的图像上任意一点,点P关于原点的对称点为P?,过P作PA平行于y轴,过P?作P?A平行于x轴,pa与P?A交于A点,则?PAP?的面积是____8_____.
第23题图
第24题图
第25题图
第26题图
第27题图
第29题图
24.
如图,点为反比例函数y=的图象上一点,点在轴上且OA=BA,则△AOB的面积为
1
.
25.如图,矩形OABC的顶点B在反比例函数y=(x>0)的图象上,S矩形OABC=6,则k=__6__.
26.如图,直线y=kx(k>0)与反比例函数y=的图象相交于点A(x1,y1),B(x2,y2),则2x1y2-7x2y1的值为__20__.
【解】 ∵点A(x1,y1)在反比例函数y=的图象上,∴y1=,即x1y1=4.∵A,B两点既在反比例函数y=的图象上,又在直线y=kx上,∴A(x1,y1),B(x2,y2)两点关于原点对称,即x1=-x2,y1=-y2,∴2x1y2-7x2y1=-2x1y1+7x1y1=5x1y1=5×4=20.
29.如图,函数与的图象交于、两点,过点作垂直于轴,垂足为,则的面积为__16__.
解:由函数与的图象交于、两点,则有点A、B关于原点对称,
∴点O为AB的中点,∴,∵AC⊥y轴,∴由反比例函数k的几何意义可得,∴,故答案为16.
30.一个正比例函数的图象与反比例函数的图象交于,两点,则的值为_
___.
解:,,两点在反比例函数的图象上,,,且,,,,,,故答案为:.
29.如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为____3_.
解:设,直线轴,,两点的纵坐标都为,而点在反比例函数的图象上,当,,即点坐标为,,又点在反比例函数的图象上,当,,即点坐标为,,,
.故答案为:3.
三.解答题(共5小题
共40分)
30.(8分)如图,一次函数y=kx+b的图象与反比例函数y=-的图象相交于点A(-1,m),B(n,-1).
(1)求一次函数的表达式.(2)求△AOB的面积.
【解】 (1)把点A(-1,m),B(n,-1)的坐标分别代入y=-,解得m=5,n=5,
∴点A(-1,5),B(5,-1).把点A(-1,5),B(5,-1)的坐标分别代入y=kx+b,得
5k+b=-1,))解得
b=4,))∴一次函数的表达式为y=-x+4.
(2)当x=0时,y=-x+4=4,∴OD=4,∴S△AOB=S△AOD+S△BOD=×4×1+×4×5=12.
31.(8分)如图,在?ABCD中,顶点A的坐标是(0,2),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是-4,?ABCD的面积是24.反比例函数y=的图象经过点B,D,求:
(1)反比例函数的表达式.(2)AB所在直线的函数表达式.
【解】 (1)∵顶点A的坐标是(0,2),顶点C的纵坐标是-4,∴AE=6.又∵?ABCD的面积是24,∴AD=BC=4,∴点D(4,2),∴k=4×2=8,∴反比例函数的表达式为y=.
(2)由题意可知,点B的纵坐标为-4,∴其横坐标为=-2,∴点B(-2,-4).设AB所在直线的函数表达式为y=kx+b,将点A(0,2),B(-2,-4)的坐标代入,得
-2k+b=-4,))解得
b=2.))∴AB所在直线的函数表达式为y=3x+2.
32.(8分)如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,C分别在x轴、y轴的正半轴上,函数y=2x的图象与CB相交于点D,函数y=(k为常数,k≠0)的图象经过点D,与AB相交于点E,与函数y=2x的图象在第三象限相交于点F,连结AF,EF.
(1)求函数y=的表达式,并直接写出E,F两点的坐标.(2)求△AEF的面积.
【解】 (1)∵正方形OABC的边长为2,
∴点D的纵坐标为2,即y=2.
将y=2代入y=2x,得x=1,∴点D的坐标为(1,2).∵函数y=的图象经过点D,∴2=,解得k=2,
∴函数y=的表达式为y=.易知点E(2,1),F(-1,-2).
(2)如解图,过点F作FG⊥AB,交BA的延长线于点G.
∵点E(2,1),F(-1,-2),∴AE=1,FG=2-(-1)=3,
∴S△AEF=AE·FG=×1×3=
33.(8分)已知等腰三角形OAB(OA=OB)在平面直角坐标系中的位置如图所示,点A的坐标为(-3,3),点B的坐标为(-6,0).
(1)若△OAB关于y轴的轴对称图形是△OA′B′,请直接写出点A,B的对称点A′,B′的坐标.
(2)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=的图象上,求a的值.
(3)若将△OAB绕点O按逆时针方向旋转∠α(0°<∠α<90°).
①当∠α=30°时,点B恰好落在反比例函数y=的图象上,求k的值.
②点A,B能否同时落在①中的反比例函数的图象上?若能,请求出∠α的度数;若不能,请说明理由.
【解】 (1)点A′(3,3),B′(6,0).
(2)当y=3时,3=,∴x=2,∴a=2-(-3)=5.
(3)①设点B旋转到点B1处,连结B1O,过点B1作B1C⊥x轴于点C.∵∠α=30°,即∠B1OC=30°,OB1=6,∴B1C=3,CO=3,∴点B1(-3,-3).把点B1(-3,-3)的坐标代入y=中,得k=9.②能.∵点A的坐标为(-3,3),∴OA=6,∴OB=6.由点A的坐标易得∠AOB=30°.当点A恰好落在反比例函数y=的图象上时,∠α=∠AOB+30°=60°,此时点B的坐标为(-3,-3).将点B的坐标代入y=,可知点B也在此反比例函数的图象上,∴∠α=60°.
34.(8分)如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且B(4,3),反比例函数的图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及点E的坐标;
(2)求直线DE的解析式.
【解】(1)∵
D(1,3)在图象上,∴∴,∴反比例函数的解析式为:,反比例函数
与AB交于点E,点B的坐标为(4,3),点E的横坐标为:4,把,代入,得,∴E.
(2)设直线DE的解析式为.∵D(1,3),E在直线DE上,
∴,解得∴直线DE的解析式为:
11.2
反比例函数的图象和性质》强化提优试卷(1)
(时间:60分钟
满分:100分)
1.选择题(共16题;共32分)
1.已知反比例函数y=的图象过点A(1,-2),则k的值为(
)
A.
1
B.
2
C.
-2
D.
-1
2.已知点A(1,-3)关于x轴的对称点A′在反比例函数y=的图象上,则实数k的值为(
)
A.
3
B.
C.
-3
D.
-
3.若反比例函数y=的图象如图所示,则一次函数y=kx+b(k≠0)的图象可能是(
)
4.对于反比例函数y=-图象对称性的叙述错误的是(
)
A.关于原点对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
5.在平面直角坐标系xOy中,反比例函数y=的图象与y=的图象关于x轴对称,且过点A(m,3),则m的值是(
)
A.2
B.-2
C.1
D.-1
6.
若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在(
)
A.第一、二象限
B.第一、三象限
C.第二、三象限
D.第二、四象限
7.若点A(3,-4),B(-2,m)在同一个反比例函数的图象上,则m的值为(
)
A.6 B.-6 C.12 D.-12
8.如图,反比例函数y=(x<0)的图象经过点P,则k的值为(
)
A.-6
B.-5
C.6
D.5
第8题图
第9题图
第10题图
第11题图
9.如图,反比例函数y=的图象与经过原点的直线l相交于A,B两点,点A的坐标为(-2,1),那么点B的坐标为(
)
A.(-2,1)
B.(2,1)
C.(1,-2)
D.(2,-1)
10.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上.若AB=1,则k的值为(
)
A.
1
B.
C.
D.
2
11.如图,函数的图象经过斜边的中点,连结.如果那么的周长为(
)
A.
B.
C.
D.
12.双曲线的图象过点,,则的值是(
)
A.
B.
C.
D.
13.在平面直角坐标系中,点,,分别在三个不同的象限,若反比例函数的图象经过其中两点,则的值为(
)
A.
B.1
C.或1
D.不能确定
14.反比例的图象经过点(-1,3),则k的值为(
)
A.
B.
C.
D.
15.一次函数与反比例函数在同一坐标系中的图象可能是(
)
A.
B.
C.D.
16.函数与在同一平面直角坐标系中的图象不可能是(
)
A.B.C.D.
2.填空题(共14题;共28分)
17.若点(a,-2a)在反比例函数y=的图象上,则此反比例函数的图象在第_______象限.
18.一次函数y=ax+b和反比例函数y=在同一坐标系内的大致图象如图所示,则a____0,b____0.
第18题图
第19题图
第20题图
第21题图
第22题图
19.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为:__________________.
20.
如图,反比例函数y=与⊙O的一个交点为P(2,1),则图中阴影部分的面积是______.
21.
如图,以原点为圆心的圆与反比例函数y=的图象交于A,B,C,D四点,已知点A的横坐标为1,则点C的横坐标为_________.
22.
如图,在直角坐标系中,点A在函数y=(x>0)的图象上,AB⊥x轴于点B,AB的垂直平分线与y轴交于点C,与函数y=(x>0)的图象交于点D,连结AC,CB,BD,DA,则四边形ACBD的面积等于_______.
23.
设是函数y=在第一象限的图像上任意一点,点P关于原点的对称点为P?,过P作PA平行于y轴,过P?作P?A平行于x轴,pa与P?A交于A点,则?PAP?的面积是_________.
第23题图
第24题图
第25题图
第26题图
第27题图
第29题图
24.
如图,点为反比例函数y=的图象上一点,点在轴上且OA=BA,则△AOB的面积为
.
25.如图,矩形OABC的顶点B在反比例函数y=(x>0)的图象上,S矩形OABC=6,则k=____.
26.如图,直线y=kx(k>0)与反比例函数y=的图象相交于点A(x1,y1),B(x2,y2),则2x1y2-7x2y1的值为____.
27.如图,函数与的图象交于、两点,过点作垂直于轴,垂足为,则的面积为____.
28.一个正比例函数的图象与反比例函数的图象交于,两点,则的值为_
___.
29.如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为_____.
3.解答题(共5小题
共40分)
30.(8分)如图,一次函数y=kx+b的图象与反比例函数y=-的图象相交于点A(-1,m),B(n,-1).
(1)求一次函数的表达式.
(2)求△AOB的面积.
31.(8分)如图,在?ABCD中,顶点A的坐标是(0,2),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是-4,?ABCD的面积是24.反比例函数y=的图象经过点B,D,求:
(1)反比例函数的表达式.
(2)AB所在直线的函数表达式.
32.(8分)如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,C分别在x轴、y轴的正半轴上,函数y=2x的图象与CB相交于点D,函数y=(k为常数,k≠0)的图象经过点D,与AB相交于点E,与函数y=2x的图象在第三象限相交于点F,连结AF,EF.
(1)求函数y=的表达式,并直接写出E,F两点的坐标.
(2)求△AEF的面积.
33.(8分)已知等腰三角形OAB(OA=OB)在平面直角坐标系中的位置如图所示,点A的坐标为(-3,3),点B的坐标为(-6,0).
(1)若△OAB关于y轴的轴对称图形是△OA′B′,请直接写出点A,B的对称点A′,B′的坐标.
(2)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=的图象上,求a的值.
(3)若将△OAB绕点O按逆时针方向旋转∠α(0°<∠α<90°).
①当∠α=30°时,点B恰好落在反比例函数y=的图象上,求k的值.
②点A,B能否同时落在①中的反比例函数的图象上?若能,请求出∠α的度数;若不能,请说明理由.
34.(8分)如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且B(4,3),反比例函数的图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及点E的坐标;
(2)求直线DE的解析式.
教师样卷
一.选择题(共16题;共32分)
1.已知反比例函数y=的图象过点A(1,-2),则k的值为(C)
A.
1
B.
2
C.
-2
D.
-1
2.已知点A(1,-3)关于x轴的对称点A′在反比例函数y=的图象上,则实数k的值为(A)
A.
3
B.
C.
-3
D.
-
3.若反比例函数y=的图象如图所示,则一次函数y=kx+b(k≠0)的图象可能是(D)
4.对于反比例函数y=-图象对称性的叙述错误的是(
D
)
A.关于原点对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
5.在平面直角坐标系xOy中,反比例函数y=的图象与y=的图象关于x轴对称,且过点A(m,3),则m的值是(
B
)
A.2
B.-2
C.1
D.-1
6.
若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在(
D
)
A.第一、二象限
B.第一、三象限
C.第二、三象限
D.第二、四象限
7.若点A(3,-4),B(-2,m)在同一个反比例函数的图象上,则m的值为(
A
)
A.6 B.-6 C.12 D.-12
8.如图,反比例函数y=(x<0)的图象经过点P,则k的值为(
A
)
A.-6
B.-5
C.6
D.5
第8题图
第9题图
第10题图
第11题图
9.如图,反比例函数y=的图象与经过原点的直线l相交于A,B两点,点A的坐标为(-2,1),那么点B的坐标为(
D
)
A.(-2,1)
B.(2,1)
C.(1,-2)
D.(2,-1)
10.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上.若AB=1,则k的值为(A)
A.
1
B.
C.
D.
2
11.如图,函数的图象经过斜边的中点,连结.如果那么的周长为(
D
)
A.
B.
C.
D.
解:如图1,过点C作CE⊥AO于E,∵点C是BO的中点∴AC=BC=CO=3,∴BO=6,∵CE⊥AO,AB⊥AO,∴AB∥CE,∴CE是的中位线,∴AB=2CE,AO=2EO,∵点在上,∴CE×EO=2,∴AB×AO=2
CE×2EO
=8,∵AB2+AO2=OB2=36,∴(AB+AO)2=36+16,∴AB+AO=
,∴△ABO的周长=AO+BO+AB=6+,故选:D.
12.双曲线的图象过点,,则的值是(
C
)
A.
B.
C.
D.
13.在平面直角坐标系中,点,,分别在三个不同的象限,若反比例函数的图象经过其中两点,则的值为(
A
)
A.
B.1
C.或1
D.不能确定
解:分三种情况:第一种情况,由,一个在第二象限,一个在第一象限,而反比例函数图象不能同时经过第一、二象限,故此情况无解;第二种情况,当反比函数经过A、C两点时,把由代入到得k=-2∴此时反比例函数的关系式为把代入得m=,
∴,其在第四象限和不在同一象限.∴m=;第三种情况,当反比函数经过B、C两点时,把代入到得k=6∴此时反比例函数的关系式为把代入得m=1,∴,其在第一象限和在同一象限.不合题意.故此情况下,无解.综上所述m=.故选:A.
14.反比例的图象经过点(-1,3),则k的值为(
C
)
A.
B.
C.
D.
15.一次函数与反比例函数在同一坐标系中的图象可能是(
D
)
A.
B.
C.D.
【详解】当时,则一次函数经过一、二、三象限,反比例函数经过一
、三象限,故排除A,C选项;当时,则一次函数经过二、三、四象限,反比例函数经过二、四象限,故排除B选项,故选择:D.
16.函数与在同一平面直角坐标系中的图象不可能是(
A
)
A.B.C.D.
二.
填空题(共14题;共28分)
17.若点(a,-2a)在反比例函数y=的图象上,则此反比例函数的图象在第二、四象限.
18.一次函数y=ax+b和反比例函数y=在同一坐标系内的大致图象如图所示,则a__<__0,b__>__0.
第18题图
第19题图
第20题图
第21题图
第22题图
19.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为:____k3>k2>k1_______________.
20.
如图,反比例函数y=与⊙O的一个交点为P(2,1),则图中阴影部分的面积是___π___.
21.
如图,以原点为圆心的圆与反比例函数y=的图象交于A,B,C,D四点,已知点A的横坐标为1,则点C的横坐标为___-3______.
22.
如图,在直角坐标系中,点A在函数y=(x>0)的图象上,AB⊥x轴于点B,AB的垂直平分线与y轴交于点C,与函数y=(x>0)的图象交于点D,连结AC,CB,BD,DA,则四边形ACBD的面积等于___4____.
23.
设是函数y=在第一象限的图像上任意一点,点P关于原点的对称点为P?,过P作PA平行于y轴,过P?作P?A平行于x轴,pa与P?A交于A点,则?PAP?的面积是____8_____.
第23题图
第24题图
第25题图
第26题图
第27题图
第29题图
24.
如图,点为反比例函数y=的图象上一点,点在轴上且OA=BA,则△AOB的面积为
1
.
25.如图,矩形OABC的顶点B在反比例函数y=(x>0)的图象上,S矩形OABC=6,则k=__6__.
26.如图,直线y=kx(k>0)与反比例函数y=的图象相交于点A(x1,y1),B(x2,y2),则2x1y2-7x2y1的值为__20__.
【解】 ∵点A(x1,y1)在反比例函数y=的图象上,∴y1=,即x1y1=4.∵A,B两点既在反比例函数y=的图象上,又在直线y=kx上,∴A(x1,y1),B(x2,y2)两点关于原点对称,即x1=-x2,y1=-y2,∴2x1y2-7x2y1=-2x1y1+7x1y1=5x1y1=5×4=20.
29.如图,函数与的图象交于、两点,过点作垂直于轴,垂足为,则的面积为__16__.
解:由函数与的图象交于、两点,则有点A、B关于原点对称,
∴点O为AB的中点,∴,∵AC⊥y轴,∴由反比例函数k的几何意义可得,∴,故答案为16.
30.一个正比例函数的图象与反比例函数的图象交于,两点,则的值为_
___.
解:,,两点在反比例函数的图象上,,,且,,,,,,故答案为:.
29.如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为____3_.
解:设,直线轴,,两点的纵坐标都为,而点在反比例函数的图象上,当,,即点坐标为,,又点在反比例函数的图象上,当,,即点坐标为,,,
.故答案为:3.
三.解答题(共5小题
共40分)
30.(8分)如图,一次函数y=kx+b的图象与反比例函数y=-的图象相交于点A(-1,m),B(n,-1).
(1)求一次函数的表达式.(2)求△AOB的面积.
【解】 (1)把点A(-1,m),B(n,-1)的坐标分别代入y=-,解得m=5,n=5,
∴点A(-1,5),B(5,-1).把点A(-1,5),B(5,-1)的坐标分别代入y=kx+b,得
5k+b=-1,))解得
b=4,))∴一次函数的表达式为y=-x+4.
(2)当x=0时,y=-x+4=4,∴OD=4,∴S△AOB=S△AOD+S△BOD=×4×1+×4×5=12.
31.(8分)如图,在?ABCD中,顶点A的坐标是(0,2),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是-4,?ABCD的面积是24.反比例函数y=的图象经过点B,D,求:
(1)反比例函数的表达式.(2)AB所在直线的函数表达式.
【解】 (1)∵顶点A的坐标是(0,2),顶点C的纵坐标是-4,∴AE=6.又∵?ABCD的面积是24,∴AD=BC=4,∴点D(4,2),∴k=4×2=8,∴反比例函数的表达式为y=.
(2)由题意可知,点B的纵坐标为-4,∴其横坐标为=-2,∴点B(-2,-4).设AB所在直线的函数表达式为y=kx+b,将点A(0,2),B(-2,-4)的坐标代入,得
-2k+b=-4,))解得
b=2.))∴AB所在直线的函数表达式为y=3x+2.
32.(8分)如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,C分别在x轴、y轴的正半轴上,函数y=2x的图象与CB相交于点D,函数y=(k为常数,k≠0)的图象经过点D,与AB相交于点E,与函数y=2x的图象在第三象限相交于点F,连结AF,EF.
(1)求函数y=的表达式,并直接写出E,F两点的坐标.(2)求△AEF的面积.
【解】 (1)∵正方形OABC的边长为2,
∴点D的纵坐标为2,即y=2.
将y=2代入y=2x,得x=1,∴点D的坐标为(1,2).∵函数y=的图象经过点D,∴2=,解得k=2,
∴函数y=的表达式为y=.易知点E(2,1),F(-1,-2).
(2)如解图,过点F作FG⊥AB,交BA的延长线于点G.
∵点E(2,1),F(-1,-2),∴AE=1,FG=2-(-1)=3,
∴S△AEF=AE·FG=×1×3=
33.(8分)已知等腰三角形OAB(OA=OB)在平面直角坐标系中的位置如图所示,点A的坐标为(-3,3),点B的坐标为(-6,0).
(1)若△OAB关于y轴的轴对称图形是△OA′B′,请直接写出点A,B的对称点A′,B′的坐标.
(2)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=的图象上,求a的值.
(3)若将△OAB绕点O按逆时针方向旋转∠α(0°<∠α<90°).
①当∠α=30°时,点B恰好落在反比例函数y=的图象上,求k的值.
②点A,B能否同时落在①中的反比例函数的图象上?若能,请求出∠α的度数;若不能,请说明理由.
【解】 (1)点A′(3,3),B′(6,0).
(2)当y=3时,3=,∴x=2,∴a=2-(-3)=5.
(3)①设点B旋转到点B1处,连结B1O,过点B1作B1C⊥x轴于点C.∵∠α=30°,即∠B1OC=30°,OB1=6,∴B1C=3,CO=3,∴点B1(-3,-3).把点B1(-3,-3)的坐标代入y=中,得k=9.②能.∵点A的坐标为(-3,3),∴OA=6,∴OB=6.由点A的坐标易得∠AOB=30°.当点A恰好落在反比例函数y=的图象上时,∠α=∠AOB+30°=60°,此时点B的坐标为(-3,-3).将点B的坐标代入y=,可知点B也在此反比例函数的图象上,∴∠α=60°.
34.(8分)如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且B(4,3),反比例函数的图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及点E的坐标;
(2)求直线DE的解析式.
【解】(1)∵
D(1,3)在图象上,∴∴,∴反比例函数的解析式为:,反比例函数
与AB交于点E,点B的坐标为(4,3),点E的横坐标为:4,把,代入,得,∴E.
(2)设直线DE的解析式为.∵D(1,3),E在直线DE上,
∴,解得∴直线DE的解析式为:
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
