江苏省恒前黄高级中学2021届高三下学期4月一模适应性考试数学试题 Word版含答案
文档属性
| 名称 | 江苏省恒前黄高级中学2021届高三下学期4月一模适应性考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 604.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-10 23:34:22 | ||
图片预览



文档简介
恒前黄高级中学2021届高三第二学期一模适应性考试
数学试卷
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求)
1.设集合false,则false
falsefalse
2.已知复数false为z的共轭复数,则false=
false
3.马林·梅森(Marin Mersenne, 1588—1648)是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物,梅森在欧几里得、费马等人研究的基础上对false作了大量的计算、验证工作,人们为纪念梅森在数论方面的这一贡献,将形如false(其中p是素数)的素数,称为梅森素数.在不超过40的素数中,随机选取两个不同的数,至少有一个为梅森素数的概率是
false
4.已知参加2020年某省夏季高考的53万名考生的成绩Z近似地服从正态分布false,估计这些考生成绩落在(552,651]的人数约为
(附:false,则false
A.3 6014 B.72 027
C. 108 041 D. 168 222
5.明朝的程大位在《算法统宗》中(1592年),有这么个算法歌诀:三人同行七十稀,五树梅花廿一枝,七子团圆正半月,除百零五便得知.它的意思是说:求某个数(正整数)的最小正整数值,可以将某数除以3所得的余数乘以70,除以5所得的余数乘以21,除以﹖所得的余数乘以15,再将所得的三个积相加,并逐次减去105,减到差小于105为止,所得结果就是这个数的最小正整数值.《孙子算经》上有一道极其有名的“物不知数"问题:“今有物不知其数﹐三三数之余二,五五数之余三,七七数之余二,问物几何.”用上面的算法歌诀来算,该物品最少是几件
A.21 B.22 C.23 D.24
6.已知△ABC中,false,动点P自点C出发沿线段CB运动,到达点B时停止,动点Q自点B出发沿线段BC运动,到达点C时停止,且动点Q的速度是动点P的2倍,若二者同时出发,且一个点停止运动时,另一个点也停止,则该过程中false的最大值是
A. B. 4 C. D. 23
7.已知函数false的大致图象如图所示,则false的解析式可能是
A.false B.false
C.false D.false
8. 如图,在四面体false中,false,false的重心为false,则false
3632200254635A. false B. false C. false D. false
多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得5分,部分选对得2分,不选或有错选的得0分.
9.下列命题为真命题的是
A.若a>b,则false B.若aC.若c>a>b>0,则false D.若a>b>c>0,则false
10.设m,n是两条不同的直线,α,β是两个不同的平面?下列说法正确的是
A.若m⊥α,n⊥α,则m//n B.若α⊥β,m⊥β,m?α,则m//α
C.若α⊥β,m?α,则false D.若m?α,n?α,m//β,n//β,则α//β
11.二项展开式false,则
false false
false false
12.已知函数false,且对任意x∈R都有false则
A.f(x)的最小正周期为2π B.f(x)在false上单调递增
false是f(x)的一个零点 false
填空题:本大题共4小题,每小题5分,共20分.请把答案填写在答题卡相应位置上.
已知双曲线false的渐近线与圆false相切,且双曲线的一个焦点与圆F的圆心重合,则双曲线C的方程为_____.
已知函数false,则x∈[-1,e]时,f(x)的最小值为_____,设false若函数g(x)有6个零点,则实数a的取值范围是_____.(本题第一空2分,第二空3分)
在△ABC中,false点D在线段AC上,且满足AD=2CD,false则sin∠CBD=_____
16.定义函数f(x)=[x[x]],其中[x]表示不超过x的最大整数,例如
[1.3]=1,[-1.5]=-2,[2]=2,当false时,f(x)的值域为false,记集合false中元素的个数为false则false值为____.
四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.
17. (10分)
已知正项数列false的前false项和为false.若false.
(1)求证:数列false是等差数列;
(2)设false,求数列false的前false项和false.
18.(12分)
在①false,②false,③三边成等比数列这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求解此三角形的边长和角的大小;若问题中的三角形不存在,请说明理由.
问题:是否存在false,它的内角false,false,false的对边分别为false,false,false,且false,false,______________?注:如果选择多个条件分别解答,按第一个解答计分.
19.(12分)
某土特产超市为预估2021年五一期间游客购买土特产的情况,对2020年五一期间的90位游客的购买情况进行统计,得到如下人数分布表.
购买金额(元)
false
false
false
false
false
false
人数
10
15
20
15
20
10
(1)根据以上数据完成false列联表,并判断是否有95%的把握认为购买金额是否少于60元与性别有关?
不少于60元
少于60元
合计
男
40
女
18
合计
90
(2)为吸引游客,该超市推出一种优惠方案,若购买金额不少于60元可抽奖3次,每次中奖概率为p(每次抽奖互不影响,且p的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数X(元)的分布列并求其数学期望.
参考公式及数据:false,其中false.
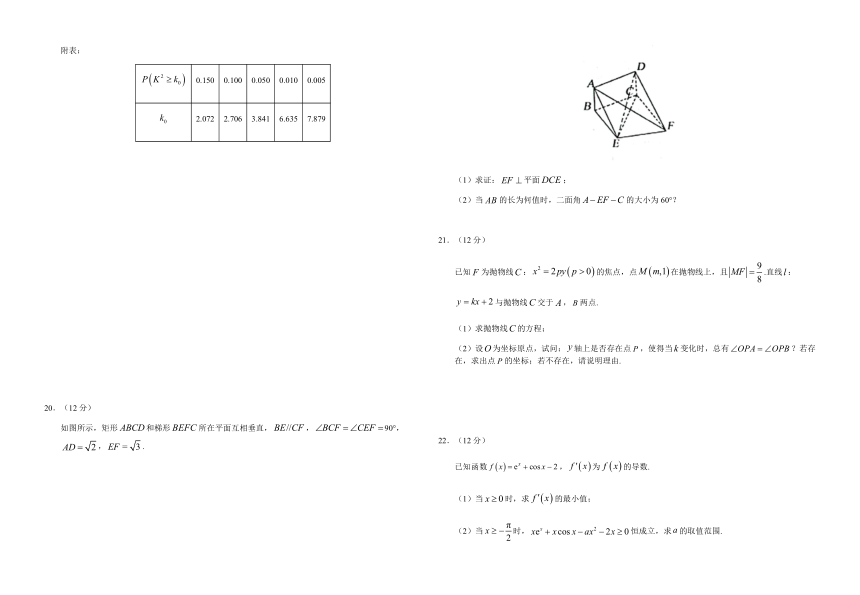
附表:
false
0.150
0.100
0.050
0.010
0.005
false
2.072
2.706
3.841
6.635
7.879
20.(12分)
如图所示,矩形false和梯形false所在平面互相垂直,false,false90°,false,false.
(1)求证:false平面false;
(2)当false的长为何值时,二面角false的大小为60°?
21.(12分)
已知false为抛物线false:false的焦点,点false在抛物线上,且false.直线false:false与抛物线false交于false,false两点.
(1)求抛物线false的方程;
(2)设false为坐标原点,试问:false轴上是否存在点false,使得当false变化时,总有false?若存在,求出点false的坐标;若不存在,请说明理由.
22.(12分)
已知函数false,false为false的导数.
(1)当false时,求false的最小值;
(2)当false时,false恒成立,求false的取值范围.
2021届高三第二学期一模适应性考试
数学试卷答案
1.B 2. D 3. A 4.B
5. C 6. C 7. C 8. C
9. CD
10. AB
11 ABC
12. ACD
13false
14 -4,false
false
false
17.(10分)
【解析】(1)由题意得,false,则false,
∴false,
∴false,由false可得false,
∴数列false是首项为1,公差为1的等差数列.(5分)
(2)由(1)可得false,∴false,
∴false,
∴falsefalse.(10分)
18.(12分)
【解析】选①,
∵在false中,false,∴由正弦定理得false,即false,
又false,∴false,(4分)
∴false,解得false,(8分)
∴false,false,false.(12分)
选②,
∵在false中,false,∴由正弦定理得false,即false,
∵false,即false,
∴false,(6分)
false,∴false,
∴false,false.(12分)
选③,
∵在false中,false,∴由正弦定理得false,
又false,∴false,即false,
即false,这与三边成等比数列矛盾,即问题中的三角形不存在.(12分)
19.(12分)
【解析】(1)false列联表如下:
不少于60元
少于60元
合计
男
12
40
52
女
18
20
38
合计
30
60
90
(2分)
若false的观测值false,(4分)
因此有95%的把握认为购买金额是否少于60元与性别有关.(5分)
(2)X的可能取值为65,70,75,80,且false.(6分)
由题意知:
false,false,
false,false,(10分)
所以X的分布列为
X
65
70
75
80
false
false
false
false
false
(11分)
false.(12分)
20.(12分)
【解析】(1)因为平面false平面false,平面false平面false,false,false平面false,所以false平面false,(2分)
又false平面false,所以false.(3分)
又因为false,false,false平面false,
所以false平面false.(4分)
(2)如图所示,以点false为坐标原点,false,false和false所在直线分别为false轴、false轴和false轴建立空间直角坐标系false.(5分)
过点false作false于点false.在false中,false,false,所以false.
因为false,所以false,
所以false,所以false,所以false,
所以false,所以false.(7分)
设false,则false,false,false,false.
所以false,false.(8分)
设平面false的法向量为false,则false,即false,
令false,得平面false的一个法向量为false.(10分)
又因为false平面false,所以平面false的一个法向量为false,
所以false,解得false,
所以当false时,二面角false的大小为60°.(12分)
21.(12分)
【解析】(1)根据抛物线的定义,得false,解得false.(2分)
∴抛物线false的方程为false.(3分)
(2)在false轴上存在点false,使得当false变化时,总有false.(4分)
理由如下:
设false,false,false.
由false消去false,得false,且false恒成立.(6分)
∴false,false,false,false.(8分)
∵false时,直线false和直线false的倾斜角互补,即其斜率互为相反数,
∴false,
∴false,即false,(10分)
∴false,得false,即点false的坐标为(0,false).
所以false轴上存在点false(0,false),使得当false变化时,总有false.(12分)
22.(12分)
【解析】(1)false,(1分)
令false,false,则false.(2分)
当false时,false,
故false时,false,false为增函数,
故false,即false的最小值为1.(4分)
(2)令false,则false,
则本题即证当false时,false恒成立.(5分)
当false时,若false,则由(1)可知,false,
所以false为增函数,故false恒成立,即false恒成立;(6分)
若false,令false,则false,
令false,则false在false上为增函数,
又false,false,故存在唯一false,使得false.
当false时,false,false为减函数;false时,false,false为增函数.
又false,false,故存在唯一false使得false.
故false时,false,false为增函数;false时,false,false为减函数.
又false,false,
所以false时,false,false为增函数,
故false,即false恒成立.(10分)
当false时,由(1)可知false在false上为增函数,
且false,false,故存在唯一false,使得false.
则当false时,false,false为减函数,
所以false,此时false,与false恒成立矛盾.
综上所述,false.(12分)
数学试卷
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求)
1.设集合false,则false
falsefalse
2.已知复数false为z的共轭复数,则false=
false
3.马林·梅森(Marin Mersenne, 1588—1648)是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物,梅森在欧几里得、费马等人研究的基础上对false作了大量的计算、验证工作,人们为纪念梅森在数论方面的这一贡献,将形如false(其中p是素数)的素数,称为梅森素数.在不超过40的素数中,随机选取两个不同的数,至少有一个为梅森素数的概率是
false
4.已知参加2020年某省夏季高考的53万名考生的成绩Z近似地服从正态分布false,估计这些考生成绩落在(552,651]的人数约为
(附:false,则false
A.3 6014 B.72 027
C. 108 041 D. 168 222
5.明朝的程大位在《算法统宗》中(1592年),有这么个算法歌诀:三人同行七十稀,五树梅花廿一枝,七子团圆正半月,除百零五便得知.它的意思是说:求某个数(正整数)的最小正整数值,可以将某数除以3所得的余数乘以70,除以5所得的余数乘以21,除以﹖所得的余数乘以15,再将所得的三个积相加,并逐次减去105,减到差小于105为止,所得结果就是这个数的最小正整数值.《孙子算经》上有一道极其有名的“物不知数"问题:“今有物不知其数﹐三三数之余二,五五数之余三,七七数之余二,问物几何.”用上面的算法歌诀来算,该物品最少是几件
A.21 B.22 C.23 D.24
6.已知△ABC中,false,动点P自点C出发沿线段CB运动,到达点B时停止,动点Q自点B出发沿线段BC运动,到达点C时停止,且动点Q的速度是动点P的2倍,若二者同时出发,且一个点停止运动时,另一个点也停止,则该过程中false的最大值是
A. B. 4 C. D. 23
7.已知函数false的大致图象如图所示,则false的解析式可能是
A.false B.false
C.false D.false
8. 如图,在四面体false中,false,false的重心为false,则false
3632200254635A. false B. false C. false D. false
多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得5分,部分选对得2分,不选或有错选的得0分.
9.下列命题为真命题的是
A.若a>b,则false B.若a
10.设m,n是两条不同的直线,α,β是两个不同的平面?下列说法正确的是
A.若m⊥α,n⊥α,则m//n B.若α⊥β,m⊥β,m?α,则m//α
C.若α⊥β,m?α,则false D.若m?α,n?α,m//β,n//β,则α//β
11.二项展开式false,则
false false
false false
12.已知函数false,且对任意x∈R都有false则
A.f(x)的最小正周期为2π B.f(x)在false上单调递增
false是f(x)的一个零点 false
填空题:本大题共4小题,每小题5分,共20分.请把答案填写在答题卡相应位置上.
已知双曲线false的渐近线与圆false相切,且双曲线的一个焦点与圆F的圆心重合,则双曲线C的方程为_____.
已知函数false,则x∈[-1,e]时,f(x)的最小值为_____,设false若函数g(x)有6个零点,则实数a的取值范围是_____.(本题第一空2分,第二空3分)
在△ABC中,false点D在线段AC上,且满足AD=2CD,false则sin∠CBD=_____
16.定义函数f(x)=[x[x]],其中[x]表示不超过x的最大整数,例如
[1.3]=1,[-1.5]=-2,[2]=2,当false时,f(x)的值域为false,记集合false中元素的个数为false则false值为____.
四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.
17. (10分)
已知正项数列false的前false项和为false.若false.
(1)求证:数列false是等差数列;
(2)设false,求数列false的前false项和false.
18.(12分)
在①false,②false,③三边成等比数列这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求解此三角形的边长和角的大小;若问题中的三角形不存在,请说明理由.
问题:是否存在false,它的内角false,false,false的对边分别为false,false,false,且false,false,______________?注:如果选择多个条件分别解答,按第一个解答计分.
19.(12分)
某土特产超市为预估2021年五一期间游客购买土特产的情况,对2020年五一期间的90位游客的购买情况进行统计,得到如下人数分布表.
购买金额(元)
false
false
false
false
false
false
人数
10
15
20
15
20
10
(1)根据以上数据完成false列联表,并判断是否有95%的把握认为购买金额是否少于60元与性别有关?
不少于60元
少于60元
合计
男
40
女
18
合计
90
(2)为吸引游客,该超市推出一种优惠方案,若购买金额不少于60元可抽奖3次,每次中奖概率为p(每次抽奖互不影响,且p的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数X(元)的分布列并求其数学期望.
参考公式及数据:false,其中false.
附表:
false
0.150
0.100
0.050
0.010
0.005
false
2.072
2.706
3.841
6.635
7.879
20.(12分)
如图所示,矩形false和梯形false所在平面互相垂直,false,false90°,false,false.
(1)求证:false平面false;
(2)当false的长为何值时,二面角false的大小为60°?
21.(12分)
已知false为抛物线false:false的焦点,点false在抛物线上,且false.直线false:false与抛物线false交于false,false两点.
(1)求抛物线false的方程;
(2)设false为坐标原点,试问:false轴上是否存在点false,使得当false变化时,总有false?若存在,求出点false的坐标;若不存在,请说明理由.
22.(12分)
已知函数false,false为false的导数.
(1)当false时,求false的最小值;
(2)当false时,false恒成立,求false的取值范围.
2021届高三第二学期一模适应性考试
数学试卷答案
1.B 2. D 3. A 4.B
5. C 6. C 7. C 8. C
9. CD
10. AB
11 ABC
12. ACD
13false
14 -4,false
false
false
17.(10分)
【解析】(1)由题意得,false,则false,
∴false,
∴false,由false可得false,
∴数列false是首项为1,公差为1的等差数列.(5分)
(2)由(1)可得false,∴false,
∴false,
∴falsefalse.(10分)
18.(12分)
【解析】选①,
∵在false中,false,∴由正弦定理得false,即false,
又false,∴false,(4分)
∴false,解得false,(8分)
∴false,false,false.(12分)
选②,
∵在false中,false,∴由正弦定理得false,即false,
∵false,即false,
∴false,(6分)
false,∴false,
∴false,false.(12分)
选③,
∵在false中,false,∴由正弦定理得false,
又false,∴false,即false,
即false,这与三边成等比数列矛盾,即问题中的三角形不存在.(12分)
19.(12分)
【解析】(1)false列联表如下:
不少于60元
少于60元
合计
男
12
40
52
女
18
20
38
合计
30
60
90
(2分)
若false的观测值false,(4分)
因此有95%的把握认为购买金额是否少于60元与性别有关.(5分)
(2)X的可能取值为65,70,75,80,且false.(6分)
由题意知:
false,false,
false,false,(10分)
所以X的分布列为
X
65
70
75
80
false
false
false
false
false
(11分)
false.(12分)
20.(12分)
【解析】(1)因为平面false平面false,平面false平面false,false,false平面false,所以false平面false,(2分)
又false平面false,所以false.(3分)
又因为false,false,false平面false,
所以false平面false.(4分)
(2)如图所示,以点false为坐标原点,false,false和false所在直线分别为false轴、false轴和false轴建立空间直角坐标系false.(5分)
过点false作false于点false.在false中,false,false,所以false.
因为false,所以false,
所以false,所以false,所以false,
所以false,所以false.(7分)
设false,则false,false,false,false.
所以false,false.(8分)
设平面false的法向量为false,则false,即false,
令false,得平面false的一个法向量为false.(10分)
又因为false平面false,所以平面false的一个法向量为false,
所以false,解得false,
所以当false时,二面角false的大小为60°.(12分)
21.(12分)
【解析】(1)根据抛物线的定义,得false,解得false.(2分)
∴抛物线false的方程为false.(3分)
(2)在false轴上存在点false,使得当false变化时,总有false.(4分)
理由如下:
设false,false,false.
由false消去false,得false,且false恒成立.(6分)
∴false,false,false,false.(8分)
∵false时,直线false和直线false的倾斜角互补,即其斜率互为相反数,
∴false,
∴false,即false,(10分)
∴false,得false,即点false的坐标为(0,false).
所以false轴上存在点false(0,false),使得当false变化时,总有false.(12分)
22.(12分)
【解析】(1)false,(1分)
令false,false,则false.(2分)
当false时,false,
故false时,false,false为增函数,
故false,即false的最小值为1.(4分)
(2)令false,则false,
则本题即证当false时,false恒成立.(5分)
当false时,若false,则由(1)可知,false,
所以false为增函数,故false恒成立,即false恒成立;(6分)
若false,令false,则false,
令false,则false在false上为增函数,
又false,false,故存在唯一false,使得false.
当false时,false,false为减函数;false时,false,false为增函数.
又false,false,故存在唯一false使得false.
故false时,false,false为增函数;false时,false,false为减函数.
又false,false,
所以false时,false,false为增函数,
故false,即false恒成立.(10分)
当false时,由(1)可知false在false上为增函数,
且false,false,故存在唯一false,使得false.
则当false时,false,false为减函数,
所以false,此时false,与false恒成立矛盾.
综上所述,false.(12分)
同课章节目录
