北师大版八年级数学下册5.4 分式方程同步练习(Word版,共2课时,附答案)
文档属性
| 名称 | 北师大版八年级数学下册5.4 分式方程同步练习(Word版,共2课时,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 37.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:17:57 | ||
图片预览




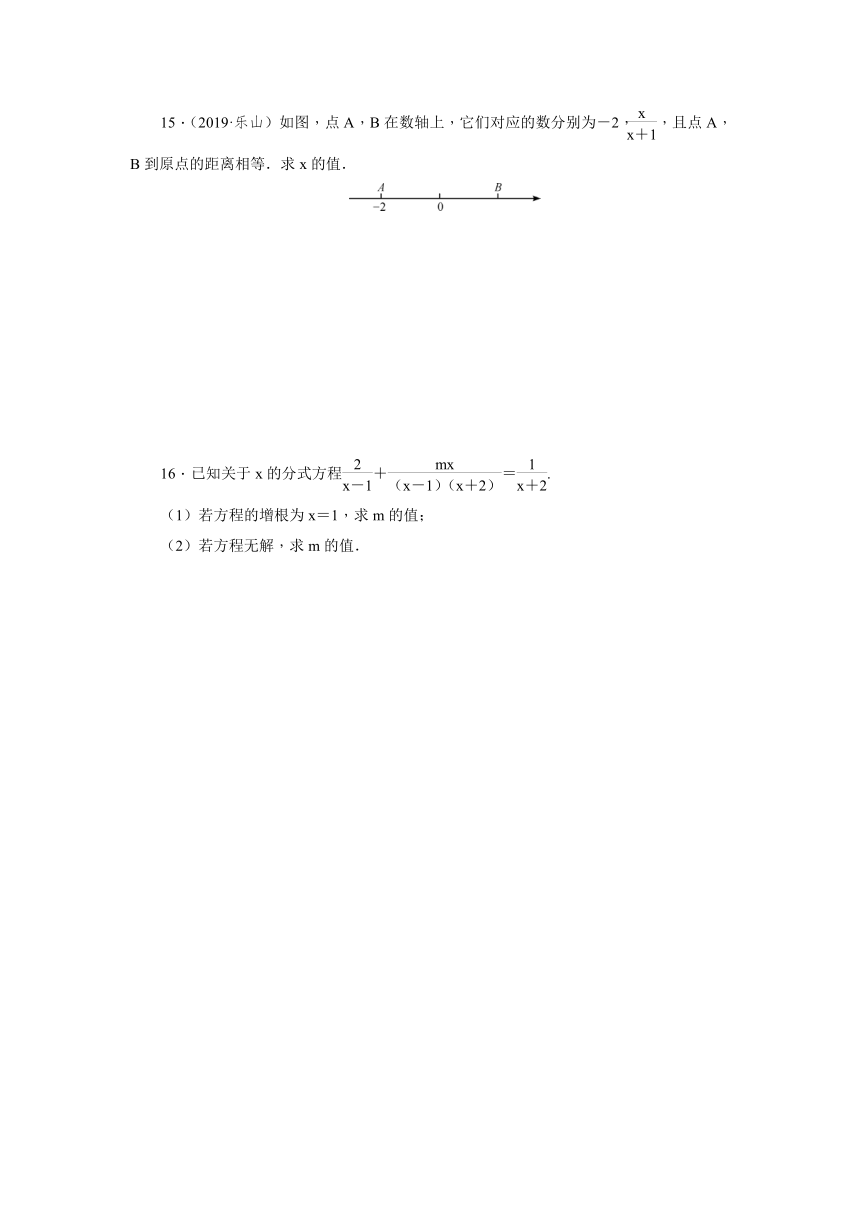
文档简介
4 分式方程
第1课时 分式方程的概念
1.下列方程是分式方程的是( )
A.= B.=-2
C.2x2+x-3=0 D.2x-5=
2.下列关于x的方程:①=+;②-=0;③mx=x+1(m,n均为常数);④=;⑤=;⑥+=(a为常数),其中整式方程是 ,分式方程是 .
3.请你利用代数式x-2,x+5,3组成一个分式方程: .
知识点2 列分式方程
4.(2020·鞍山)甲、乙两人加工某种机器零件,已知每小时甲比乙少加工6个这种零件,甲加工240个这种零件所用的时间与乙加工300个这种零件所用的时间相等,设甲每小时加工x个零件,所列方程正确的是( )
A.= B.=
C.= D.=
5.(2020·荆州)八年级学生去距学校10 km的荆州博物馆参观,一部分学生骑自行车先走,过了20 min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.若设骑车学生的速度为x km/h,则可列方程为( )
A.-=20 B.-=20
C.-= D.-=
6.为创建绿色文明城市,我市某城区对一条全长12 000 m的公路进行绿化带改造,计划每天完成绿化带改造任务x m,当x满足的方程为×=时,下列对这一方程所反映的数量关系描述正确的是( )
A.实际每天比计划多完成改造任务300 m,实际所用天数是计划的
B.实际每天比计划少完成改造任务300 m,计划所用天数是实际的
C.实际每天比计划多完成改造任务300 m,计划所用天数是实际的
D.实际每天比计划少完成改造任务300 m,实际所用天数是计划的
7.(2020·自贡)某工程队承接了80万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了35%,结果提前40天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )
A.-=40
B.-=40
C.-=40
D.-=40
8.某工程在进行招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,有如下方案:
Ⅰ.甲队单独完成这项工程刚好如期完成;
Ⅱ.乙队单独完成这项工程要比规定日期多6天;
Ⅲ.若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
(1)设甲队单独完成这项工程需要x天,请将下表补充完整;
工程总量
所用时间(天)
工程效率
甲队
1
x
乙队
1
x+6
(2)根据题意及表中所得到的信息列出方程.
第2课时 分式方程的解法
知识点1 分式方程的解法
1.(2019·益阳)解分式方程+=3时,去分母化为一元一次方程,正确的是( )
A.x+2=3 B.x-2=3
C.x-2=3(2x-1) D.x+2=3(2x-1)
2.(2020·海南)分式方程=1的解是( )
A.x=-1 B.x=1
C.x=5 D.x=2
3.(2020·哈尔滨)方程=的解为( )
A.x=-1 B.x=5
C.x=7 D.x=9
4.(2019·成都)分式方程+=1的解为( )
A.x=-1 B.x=1
C.x=2 D.x=-2
5.若与互为相反数,则x等于( )
A.-1 B.-2 C.2 D.0
6.(2019·天水)分式方程-=0的解是 .
7.解方程:
(1)(2020·通辽)=; (2)(2020·常州)+=2.
知识点2 分式方程的增根
8.若分式方程=+有增根,则增根可能是( )
A.0 B.2
C.0或2 D.1
9.(2020·遂宁)关于x的分式方程-=1有增根,则m的值为( )
A.m=2 B.m=1
C.m=3 D.m=-3
易错点1 去分母时,常数项漏乘最简公分母而出错
10.(2020·陕西)解分式方程:-=1.
易错点2 考虑问题不全面致错
(2020·眉山)关于x的分式方程+2=的解为正实数,则k的取值范围是
.
12.(2019·襄阳)定义:a*b=,则方程2*(x+3)=1*(2x)的解为 .
13.解方程:
(1)(2019·广安)-1=; (2)(2019·宁夏)+1=;
(3)=+.
14.设A=,B=+1.
(1)求当x为何值时,A=2;
(2)若A与B的值相等,求x的值.
15.(2019·乐山)如图,点A,B在数轴上,它们对应的数分别为-2,,且点A,B到原点的距离相等.求x的值.
16.已知关于x的分式方程+=.
(1)若方程的增根为x=1,求m的值;
(2)若方程无解,求m的值.
参考答案:
4 分式方程
第1课时 分式方程的概念
1.下列方程是分式方程的是(A)
A.= B.=-2
C.2x2+x-3=0 D.2x-5=
2.下列关于x的方程:①=+;②-=0;③mx=x+1(m,n均为常数);④=;⑤=;⑥+=(a为常数),其中整式方程是②③④⑥,分式方程是①⑤.
3.请你利用代数式x-2,x+5,3组成一个分式方程:=3(答案不唯一,合理即可).
4.(2020·鞍山)甲、乙两人加工某种机器零件,已知每小时甲比乙少加工6个这种零件,甲加工240个这种零件所用的时间与乙加工300个这种零件所用的时间相等,设甲每小时加工x个零件,所列方程正确的是(B)
A.= B.=
C.= D.=
5.(2020·荆州)八年级学生去距学校10 km的荆州博物馆参观,一部分学生骑自行车先走,过了20 min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.若设骑车学生的速度为x km/h,则可列方程为(C)
A.-=20 B.-=20
C.-= D.-=
6.为创建绿色文明城市,我市某城区对一条全长12 000 m的公路进行绿化带改造,计划每天完成绿化带改造任务x m,当x满足的方程为×=时,下列对这一方程所反映的数量关系描述正确的是(A)
A.实际每天比计划多完成改造任务300 m,实际所用天数是计划的
B.实际每天比计划少完成改造任务300 m,计划所用天数是实际的
C.实际每天比计划多完成改造任务300 m,计划所用天数是实际的
D.实际每天比计划少完成改造任务300 m,实际所用天数是计划的
7.(2020·自贡)某工程队承接了80万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了35%,结果提前40天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是(A)
A.-=40
B.-=40
C.-=40
D.-=40
8.某工程在进行招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,有如下方案:
Ⅰ.甲队单独完成这项工程刚好如期完成;
Ⅱ.乙队单独完成这项工程要比规定日期多6天;
Ⅲ.若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
(1)设甲队单独完成这项工程需要x天,请将下表补充完整;
工程总量
所用时间(天)
工程效率
甲队
1
x
乙队
1
x+6
(2)根据题意及表中所得到的信息列出方程.
解:(+)×3+(x-3)×=1.
第2课时 分式方程的解法
1.(2019·益阳)解分式方程+=3时,去分母化为一元一次方程,正确的是(C)
A.x+2=3 B.x-2=3
C.x-2=3(2x-1) D.x+2=3(2x-1)
2.(2020·海南)分式方程=1的解是(C)
A.x=-1 B.x=1
C.x=5 D.x=2
3.(2020·哈尔滨)方程=的解为(D)
A.x=-1 B.x=5
C.x=7 D.x=9
4.(2019·成都)分式方程+=1的解为(A)
A.x=-1 B.x=1
C.x=2 D.x=-2
5.若与互为相反数,则x等于(D)
A.-1 B.-2 C.2 D.0
6.(2019·天水)分式方程-=0的解是x=2.
7.解方程:
(1)(2020·通辽)=;
解:方程两边都乘x(x-2),得2x=3x-6.
解得x=6.
检验:当x=6时,x(x-2)=6×4=24≠0,
∴原分式方程的解是x=6.
(2)(2020·常州)+=2.
解:方程两边同乘(x-1),得x-2=2(x-1).
解得x=0.
检验:当x=0时,x-1≠0.
∴原分式方程的解是x=0.
知识点2 分式方程的增根
8.若分式方程=+有增根,则增根可能是(C)
A.0 B.2
C.0或2 D.1
9.(2020·遂宁)关于x的分式方程-=1有增根,则m的值为(D)
A.m=2 B.m=1
C.m=3 D.m=-3
易错点1 去分母时,常数项漏乘最简公分母而出错
10.(2020·陕西)解分式方程:-=1.
解:方程两边同乘x(x-2),得
(x-2)2-3x=x(x-2),
解得x=.
检验:当x=时,x(x-2)≠0.
∴原分式方程的解是x=.
易错点2 考虑问题不全面致错
11.(2020·眉山)关于x的分式方程+2=的解为正实数,则k的取值范围是k>-2且k≠2.
12.(2019·襄阳)定义:a*b=,则方程2*(x+3)=1*(2x)的解为x=1.
13.解方程:
(1)(2019·广安)-1=;
解:方程两边同时乘(x-2)2,得
x(x-2)-(x-2)2=4.
解得x=4.
检验:当x=4时,(x-2)2=4≠0.
∴原方程的根为x=4.
(2)(2019·宁夏)+1=;
解:方程两边同时乘(x+2)(x-1),得
2(x-1)+(x+2)(x-1)=x(x+2).
解得x=4.
检验:当x=4时,(x+2)(x-1)=18≠0.
∴原方程的根为x=4.
(3)=+.
解:去分母,得(x-2)2=(x+2)2+16,
整理,得x2-4x+4=x2+4x+4+16,
解得x=-2.
检验:当x=-2时,x2-4=0,
∴原分式方程无解.
14.设A=,B=+1.
(1)求当x为何值时,A=2;
(2)若A与B的值相等,求x的值.
解:(1)令A=2,即=2.
去分母,得2x-2=x.
解得x=2.
经检验,x=2是分式方程的根.
∴当x=2时,A=2.
(2)当A=B时,得=+1.
两边同时乘(x+1)(x-1),得
x(x+1)=3+(x+1)(x-1).
∴x2+x=3+x2-1.
解得x=2.
经检验,x=2是分式方程的根.
∴当x=2时,A=B.
15.(2019·乐山)如图,点A,B在数轴上,它们对应的数分别为-2,,且点A,B到原点的距离相等.求x的值.
解:根据题意,得=2.
去分母,得x=2(x+1).
解得x=-2.
检验:当x=-2时,x+1=-1≠0.
∴x=-2是原方程的解.
∴x的值为-2.
16.已知关于x的分式方程+=.
(1)若方程的增根为x=1,求m的值;
(2)若方程无解,求m的值.
解:方程两边同时乘(x+2)(x-1),
去分母,并整理得(m+1)x=-5.
(1)∵x=1是分式方程的增根,
∴1+m=-5.
解得m=-6.
(2)当m+1=0时,该方程无解,此时m=-1;
当m+1≠0时,要使原方程无解,
则x=1或x=-2.
当x=1时,由(1)得m=-6;
当x=-2时,则-2(m+1)=-5,
解得m=.
综上,m的值为-1或-6或.
第1课时 分式方程的概念
1.下列方程是分式方程的是( )
A.= B.=-2
C.2x2+x-3=0 D.2x-5=
2.下列关于x的方程:①=+;②-=0;③mx=x+1(m,n均为常数);④=;⑤=;⑥+=(a为常数),其中整式方程是 ,分式方程是 .
3.请你利用代数式x-2,x+5,3组成一个分式方程: .
知识点2 列分式方程
4.(2020·鞍山)甲、乙两人加工某种机器零件,已知每小时甲比乙少加工6个这种零件,甲加工240个这种零件所用的时间与乙加工300个这种零件所用的时间相等,设甲每小时加工x个零件,所列方程正确的是( )
A.= B.=
C.= D.=
5.(2020·荆州)八年级学生去距学校10 km的荆州博物馆参观,一部分学生骑自行车先走,过了20 min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.若设骑车学生的速度为x km/h,则可列方程为( )
A.-=20 B.-=20
C.-= D.-=
6.为创建绿色文明城市,我市某城区对一条全长12 000 m的公路进行绿化带改造,计划每天完成绿化带改造任务x m,当x满足的方程为×=时,下列对这一方程所反映的数量关系描述正确的是( )
A.实际每天比计划多完成改造任务300 m,实际所用天数是计划的
B.实际每天比计划少完成改造任务300 m,计划所用天数是实际的
C.实际每天比计划多完成改造任务300 m,计划所用天数是实际的
D.实际每天比计划少完成改造任务300 m,实际所用天数是计划的
7.(2020·自贡)某工程队承接了80万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了35%,结果提前40天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )
A.-=40
B.-=40
C.-=40
D.-=40
8.某工程在进行招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,有如下方案:
Ⅰ.甲队单独完成这项工程刚好如期完成;
Ⅱ.乙队单独完成这项工程要比规定日期多6天;
Ⅲ.若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
(1)设甲队单独完成这项工程需要x天,请将下表补充完整;
工程总量
所用时间(天)
工程效率
甲队
1
x
乙队
1
x+6
(2)根据题意及表中所得到的信息列出方程.
第2课时 分式方程的解法
知识点1 分式方程的解法
1.(2019·益阳)解分式方程+=3时,去分母化为一元一次方程,正确的是( )
A.x+2=3 B.x-2=3
C.x-2=3(2x-1) D.x+2=3(2x-1)
2.(2020·海南)分式方程=1的解是( )
A.x=-1 B.x=1
C.x=5 D.x=2
3.(2020·哈尔滨)方程=的解为( )
A.x=-1 B.x=5
C.x=7 D.x=9
4.(2019·成都)分式方程+=1的解为( )
A.x=-1 B.x=1
C.x=2 D.x=-2
5.若与互为相反数,则x等于( )
A.-1 B.-2 C.2 D.0
6.(2019·天水)分式方程-=0的解是 .
7.解方程:
(1)(2020·通辽)=; (2)(2020·常州)+=2.
知识点2 分式方程的增根
8.若分式方程=+有增根,则增根可能是( )
A.0 B.2
C.0或2 D.1
9.(2020·遂宁)关于x的分式方程-=1有增根,则m的值为( )
A.m=2 B.m=1
C.m=3 D.m=-3
易错点1 去分母时,常数项漏乘最简公分母而出错
10.(2020·陕西)解分式方程:-=1.
易错点2 考虑问题不全面致错
(2020·眉山)关于x的分式方程+2=的解为正实数,则k的取值范围是
.
12.(2019·襄阳)定义:a*b=,则方程2*(x+3)=1*(2x)的解为 .
13.解方程:
(1)(2019·广安)-1=; (2)(2019·宁夏)+1=;
(3)=+.
14.设A=,B=+1.
(1)求当x为何值时,A=2;
(2)若A与B的值相等,求x的值.
15.(2019·乐山)如图,点A,B在数轴上,它们对应的数分别为-2,,且点A,B到原点的距离相等.求x的值.
16.已知关于x的分式方程+=.
(1)若方程的增根为x=1,求m的值;
(2)若方程无解,求m的值.
参考答案:
4 分式方程
第1课时 分式方程的概念
1.下列方程是分式方程的是(A)
A.= B.=-2
C.2x2+x-3=0 D.2x-5=
2.下列关于x的方程:①=+;②-=0;③mx=x+1(m,n均为常数);④=;⑤=;⑥+=(a为常数),其中整式方程是②③④⑥,分式方程是①⑤.
3.请你利用代数式x-2,x+5,3组成一个分式方程:=3(答案不唯一,合理即可).
4.(2020·鞍山)甲、乙两人加工某种机器零件,已知每小时甲比乙少加工6个这种零件,甲加工240个这种零件所用的时间与乙加工300个这种零件所用的时间相等,设甲每小时加工x个零件,所列方程正确的是(B)
A.= B.=
C.= D.=
5.(2020·荆州)八年级学生去距学校10 km的荆州博物馆参观,一部分学生骑自行车先走,过了20 min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.若设骑车学生的速度为x km/h,则可列方程为(C)
A.-=20 B.-=20
C.-= D.-=
6.为创建绿色文明城市,我市某城区对一条全长12 000 m的公路进行绿化带改造,计划每天完成绿化带改造任务x m,当x满足的方程为×=时,下列对这一方程所反映的数量关系描述正确的是(A)
A.实际每天比计划多完成改造任务300 m,实际所用天数是计划的
B.实际每天比计划少完成改造任务300 m,计划所用天数是实际的
C.实际每天比计划多完成改造任务300 m,计划所用天数是实际的
D.实际每天比计划少完成改造任务300 m,实际所用天数是计划的
7.(2020·自贡)某工程队承接了80万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了35%,结果提前40天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是(A)
A.-=40
B.-=40
C.-=40
D.-=40
8.某工程在进行招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,有如下方案:
Ⅰ.甲队单独完成这项工程刚好如期完成;
Ⅱ.乙队单独完成这项工程要比规定日期多6天;
Ⅲ.若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
(1)设甲队单独完成这项工程需要x天,请将下表补充完整;
工程总量
所用时间(天)
工程效率
甲队
1
x
乙队
1
x+6
(2)根据题意及表中所得到的信息列出方程.
解:(+)×3+(x-3)×=1.
第2课时 分式方程的解法
1.(2019·益阳)解分式方程+=3时,去分母化为一元一次方程,正确的是(C)
A.x+2=3 B.x-2=3
C.x-2=3(2x-1) D.x+2=3(2x-1)
2.(2020·海南)分式方程=1的解是(C)
A.x=-1 B.x=1
C.x=5 D.x=2
3.(2020·哈尔滨)方程=的解为(D)
A.x=-1 B.x=5
C.x=7 D.x=9
4.(2019·成都)分式方程+=1的解为(A)
A.x=-1 B.x=1
C.x=2 D.x=-2
5.若与互为相反数,则x等于(D)
A.-1 B.-2 C.2 D.0
6.(2019·天水)分式方程-=0的解是x=2.
7.解方程:
(1)(2020·通辽)=;
解:方程两边都乘x(x-2),得2x=3x-6.
解得x=6.
检验:当x=6时,x(x-2)=6×4=24≠0,
∴原分式方程的解是x=6.
(2)(2020·常州)+=2.
解:方程两边同乘(x-1),得x-2=2(x-1).
解得x=0.
检验:当x=0时,x-1≠0.
∴原分式方程的解是x=0.
知识点2 分式方程的增根
8.若分式方程=+有增根,则增根可能是(C)
A.0 B.2
C.0或2 D.1
9.(2020·遂宁)关于x的分式方程-=1有增根,则m的值为(D)
A.m=2 B.m=1
C.m=3 D.m=-3
易错点1 去分母时,常数项漏乘最简公分母而出错
10.(2020·陕西)解分式方程:-=1.
解:方程两边同乘x(x-2),得
(x-2)2-3x=x(x-2),
解得x=.
检验:当x=时,x(x-2)≠0.
∴原分式方程的解是x=.
易错点2 考虑问题不全面致错
11.(2020·眉山)关于x的分式方程+2=的解为正实数,则k的取值范围是k>-2且k≠2.
12.(2019·襄阳)定义:a*b=,则方程2*(x+3)=1*(2x)的解为x=1.
13.解方程:
(1)(2019·广安)-1=;
解:方程两边同时乘(x-2)2,得
x(x-2)-(x-2)2=4.
解得x=4.
检验:当x=4时,(x-2)2=4≠0.
∴原方程的根为x=4.
(2)(2019·宁夏)+1=;
解:方程两边同时乘(x+2)(x-1),得
2(x-1)+(x+2)(x-1)=x(x+2).
解得x=4.
检验:当x=4时,(x+2)(x-1)=18≠0.
∴原方程的根为x=4.
(3)=+.
解:去分母,得(x-2)2=(x+2)2+16,
整理,得x2-4x+4=x2+4x+4+16,
解得x=-2.
检验:当x=-2时,x2-4=0,
∴原分式方程无解.
14.设A=,B=+1.
(1)求当x为何值时,A=2;
(2)若A与B的值相等,求x的值.
解:(1)令A=2,即=2.
去分母,得2x-2=x.
解得x=2.
经检验,x=2是分式方程的根.
∴当x=2时,A=2.
(2)当A=B时,得=+1.
两边同时乘(x+1)(x-1),得
x(x+1)=3+(x+1)(x-1).
∴x2+x=3+x2-1.
解得x=2.
经检验,x=2是分式方程的根.
∴当x=2时,A=B.
15.(2019·乐山)如图,点A,B在数轴上,它们对应的数分别为-2,,且点A,B到原点的距离相等.求x的值.
解:根据题意,得=2.
去分母,得x=2(x+1).
解得x=-2.
检验:当x=-2时,x+1=-1≠0.
∴x=-2是原方程的解.
∴x的值为-2.
16.已知关于x的分式方程+=.
(1)若方程的增根为x=1,求m的值;
(2)若方程无解,求m的值.
解:方程两边同时乘(x+2)(x-1),
去分母,并整理得(m+1)x=-5.
(1)∵x=1是分式方程的增根,
∴1+m=-5.
解得m=-6.
(2)当m+1=0时,该方程无解,此时m=-1;
当m+1≠0时,要使原方程无解,
则x=1或x=-2.
当x=1时,由(1)得m=-6;
当x=-2时,则-2(m+1)=-5,
解得m=.
综上,m的值为-1或-6或.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
