北师大版数学八年级下册第五章分式与分式方程专题练习(word版附答案)
文档属性
| 名称 | 北师大版数学八年级下册第五章分式与分式方程专题练习(word版附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 60.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 09:11:32 | ||
图片预览

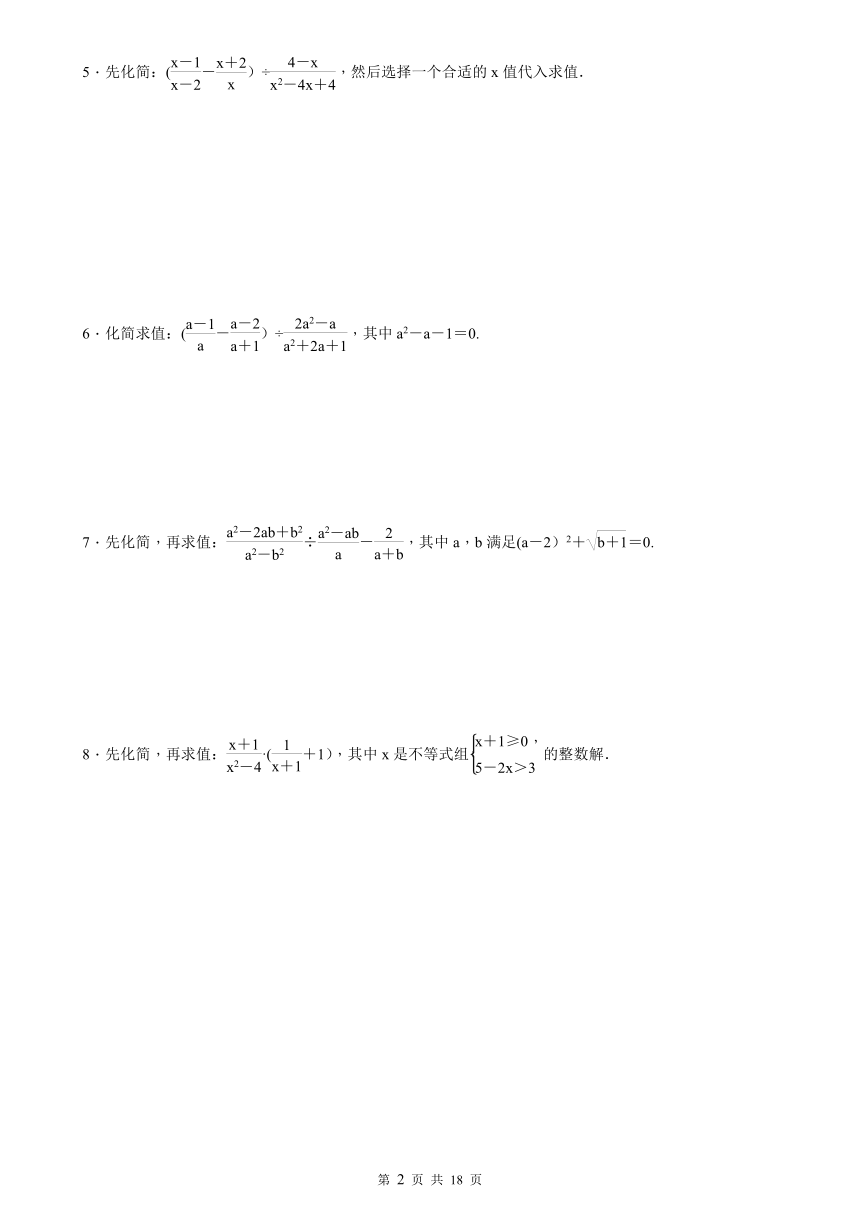
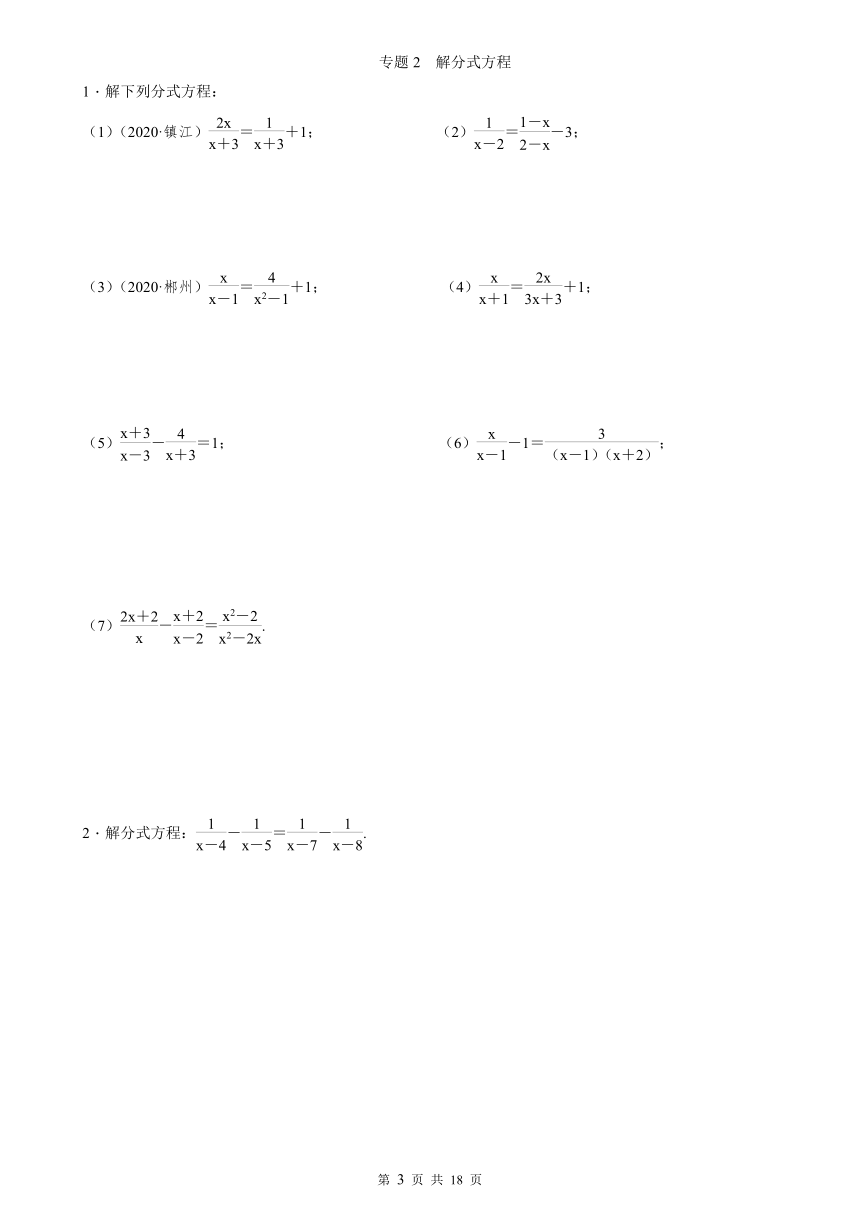


文档简介
专题1 分式的运算及化简求值
类型1 分式的运算
1.计算:
(1)(x+1)÷(1+); (2)-÷;
(3)÷(1-); (4)(-)3·(-)2÷(-)4;
(5)÷(x+); (6)(m+2+)·;
(7)(-a-1)÷; (8)1-(+)÷.
类型2 分式的化简求值
2.先化简,再求值:(1-)÷,其中a=+1.
3.先化简,再求值:(-)÷,其中x=+1,y=-1.
4. 已知y=,且x≠y,求(+)÷的值.
5.先化简:(-)÷,然后选择一个合适的x值代入求值.
6.化简求值:(-)÷,其中a2-a-1=0.
7.先化简,再求值:÷-,其中a,b满足(a-2)2+=0.
8.先化简,再求值:·(+1),其中x是不等式组的整数解.
专题2 解分式方程
1.解下列分式方程:
(1)(2020·镇江)=+1; (2)=-3;
(3)(2020·郴州)=+1; (4)=+1;
(5)-=1; (6)-1=;
(7)-=.
2.解分式方程:-=-.
专题3 由分式方程根的情况确定字母的取值范围
类型1 由特殊解确定字母的取值范围
由特殊解确定字母的取值范围的一般步骤如下:
(1)求出分式方程的根(用含有字母的式子表示);
(2)由分式方程的根为特殊解列出关于字母的不等式,并求出解集;
(3)由分式方程的解必须使分母不为0,列出关于字母的不等式,并求出解集;
(4)求(2)(3)中两个解集的公共部分即可.
1.关于x的分式方程=1的解为负数,则a的取值范围是( )
A.a>1 B.a<1
C.a<1且a≠-2 D.a>1且a≠2
2.(2020·齐齐哈尔)若关于x的分式方程=+5的解为正数,则m的取值范围为( )
A.m<-10
B.m≤-10
C.m≥-10且m≠-6
D.m>-10且m≠-6
3.(2020·黑龙江)已知关于x的分式方程-4=的解为非正数,则k的取值范围是( )
A.k≤-12 B.k≥-12
C.k>-12 D.k<-12
4.(2020·泸州)已知关于x的分式方程+2=-的解为非负数,则正整数m的所有个数为( )
A.3 B.4 C.5 D.6
5.已知关于x的分式方程-2=有一个正数解,则k的取值范围为 .
【易错提示】 求得的未知数不仅要满足所给出的范围,还要使分式的分母不为零,两个条件必须同时具备,缺一不可.
类型2 与不等式组的解集结合确定字母的取值
与不等式组的解集结合,确定字母的取值的一般步骤如下:
(1)由分式方程的根为特殊解确定字母的取值范围(方法同类型1);
(2)由不等式组的解集确定字母的取值范围;
(3)取(1)(2)中两个解集的公共部分即可.
6.(2020·重庆A卷)若关于x的一元一次不等式组的解集为x≤a;且关于y的分式方程+=1有正整数解,则所有满足条件的整数a的值之积是( )
A.7 B.-14
C.28 D.-56
7.(2020·云南)若整数a使关于x的不等式组有且只有45个整数解,且使关于y的方程+=1的解为非正数,则a的值为( )
A.-61或-58 B.-61或-59
C.-60或-59 D.-61或-60或-59
8.(2020·内江)若数a使关于x的分式方程+=3的解为非负数,且使关于y的不等式组的解集为y≤0,则符合条件的所有整数a的积为 .
类型3 由无解确定字母的取值
分式方程无解可能有两种情况:(1)去分母后化成的整式方程有解,但这个解使原方程的最简公分母为0,即是方程的增根;(2)去分母后化成的整式方程无解,即ax=b中,a=0且b≠0.
9.若关于x的方程=2+无解,则m的值为( )
A.-5 B.-8
C.-2 D.5
10.(2020·潍坊)若关于x的分式方程=+1有增根,则m= .
11.【分类讨论思想】若关于x的方程=+1无解,则a的值是 .
专题4 分式方程的应用
类型1 工程问题
1.(2020·威海)在“旅游示范公路”建设的过程中,工程队计划在海边某路段修建一条长1 200 m的步行道.由于采用新的施工方式,平均每天修建步行道的长度是计划的1.5倍,结果提前5天完成任务.求计划平均每天修建步行道的长度.
2.某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
3.(2020·益阳)新冠肺炎疫情暴发后,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有7人不能到厂生产.为了应对疫情,已复产的工人加班生产,由原来每天工作8小时增加到10小时,每小时完成的工作量不变.原来每天能生产防护服800套,现在每天能生产防护服650套.
(1)求原来生产防护服的工人有多少人?
(2)复工10天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时.公司决定将复工后生产的防护服14 500套捐献给某地,则至少还需要生产多少天才能完成任务?
4.一项工程,甲、乙两公司合作,12天可以完成,共需付施工费102 000元;如果甲、乙两公司单独完成此项工程,乙公司所用的时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1 500元.
(1)甲、乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
类型2 行程问题
5.(2020·泰州)近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线A为全程25 km的普通道路,路线B包含快速通道,全程30 km,走路线B比走路线A平均速度提高50%,时间节省6 min,求走路线B的平均速度.
6.甲、乙两同学与学校的距离均为3 000米,甲同学先步行600米然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行的速度是乙骑自行车速度的,公交车速度是乙骑自行车速度的2倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
类型3 购买与销售问题
7.(2019·泰安)端午节是我国的传统节日,人们素有吃粽子的习俗.某商场在端午节来临之际用3 000元购进A,B两种粽子1 100个,购买A种粽子与购买B种粽子的费用相同.已知A种粽子的单价是B种粽子单价的1.2倍.
(1)求A,B两种粽子的单价各是多少?
(2)若计划用不超过7 000元的资金再次购进A,B两种粽子共2 600个,已知A,B两种粽子的进价不变.求A种粽子最多能购进多少个?
8.(2020·黔西南)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,则今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1 500元和18 00元,计划B型车销售价格为2 400元,应如何组织进货才能使这批自行车销售获利最多?
参考答案:
专题1 分式的运算及化简求值
类型1 分式的运算
1.计算:
(1)(x+1)÷(1+);
解:原式=(x+1)÷
=(x+1)·
=x.
(2)-÷;
解:原式=-·
=-
=.
(3)÷(1-);
解:原式=÷
=·
=2.
(4)(-)3·(-)2÷(-)4;
解:原式=-·÷
=-a2b3c·
=-.
(5)÷(x+);
解:原式=÷(+)
=÷
=·
=.
(6)(m+2+)·;
解:原式=·
=·
=m+1.
(7)(-a-1)÷;
解:原式=(-)÷
=·
=.
(8)1-(+)÷.
解:原式=1-·
=1-
=
=.
类型2 分式的化简求值
2.先化简,再求值:(1-)÷,其中a=+1.
解:原式=·
=a-1.
当a=+1时,原式=+1-1=.
3.先化简,再求值:(-)÷,其中x=+1,y=-1.
解:原式=[-]÷
=·
=.
当x=+1,y=-1时,原式==2-.
4. 已知y=,且x≠y,求(+)÷的值.
解:原式=÷
=·
=.
∵y=,∴xy=2.
∴原式==1.
5.先化简:(-)÷,然后选择一个合适的x值代入求值.
解:原式=[-]·
=·
=.
要使分式有意义,则x(x-2)≠0,4-x≠0,
∴x≠0,2,4.
当x=1时,原工==-1.(答案不唯一,x不取0,2,4即可)
6.化简求值:(-)÷,其中a2-a-1=0.
解:原式=·
=·
=.
∵a2-a-1=0.∴a2=a+1.
∴原式==1.
7.先化简,再求值:÷-,其中a,b满足(a-2)2+=0.
解:原式=·-
=-
=-.
∵a,b满足(a-2)2+=0,
∴a-2=0,b+1=0.
∴a=2,b=-1.
∴原式=-=-1.
8.先化简,再求值:·(+1),其中x是不等式组的整数解.
解:原式=·
=
=.
解不等式组得-1≤x<1.
∵x是不等式组的整数解,
∴x=-1,0.
∵当x=-1时,原分式无意义,
∴x=0.
当x=0时,原式==-.
专题2 解分式方程
1.解下列分式方程:
(1)(2020·镇江)=+1;
解:去分母,得2x=1+x+3,
解得x=4.
检验:当x=4时,x+3≠0.
所以原方程的解是x=4.
(2)=-3;
解:方程两边同乘(x-2),得1=x-1-3x+6.
解得x=2.
检验:当x=2时,x-2=0,
所以x=2是原方程的增根,原方程无解.
(3)(2020·郴州)=+1;
解:方程两边都乘(x-1)(x+1),得
x(x+1)=4+(x-1)(x+1),
解得x=3.
检验:当x=3时,(x-1)(x+1)=8≠0.
故x=3是原方程的解.
(4)=+1;
解:去分母,得3x=2x+3x+3.
解得x=-.
检验:当x=-时,3(x+1)≠0,
所以x=-为原方程的解.
(5)-=1;
解:去分母,得(x+3)2-4(x-3)=(x-3)(x+3).
解得x=-15.
检验:当x=-15时,(x-3)(x+3)≠0,
所以原分式方程的解为x=-15.
(6)-1=;
解:去分母,得x(x+2)-(x-1)(x+2)=3.
去括号,得x2+2x-x2-2x+x+2=3.
解得x=1.
检验:当x=1时,(x-1)(x+2)=0,
所以x=1是原方程的增根,原方程无解.
(7)-=.
解:方程两边同乘x(x-2),得
(x-2)(2x+2)-x(x+2)=x2-2.
解得x=-.
检验:当x=-时,x(x-2)≠0,
所以x=-是原方程的解.
2.解分式方程:-=-.
解:两边通分,得
=,
=,
去分母,整理,得6x=36,
解得x=6.
检验:当x=6时,(x-4)(x-5)(x-7)(x-8)≠0,
所以x=6是原分式方程的解.
专题3 由分式方程根的情况确定字母的取值范围
1.关于x的分式方程=1的解为负数,则a的取值范围是(D)
A.a>1 B.a<1
C.a<1且a≠-2 D.a>1且a≠2
2.(2020·齐齐哈尔)若关于x的分式方程=+5的解为正数,则m的取值范围为(D)
A.m<-10
B.m≤-10
C.m≥-10且m≠-6
D.m>-10且m≠-6
3.(2020·黑龙江)已知关于x的分式方程-4=的解为非正数,则k的取值范围是(A)
A.k≤-12 B.k≥-12
C.k>-12 D.k<-12
4.(2020·泸州)已知关于x的分式方程+2=-的解为非负数,则正整数m的所有个数为(B)
A.3 B.4 C.5 D.6
5.已知关于x的分式方程-2=有一个正数解,则k的取值范围为k<6且k≠3.
6.(2020·重庆A卷)若关于x的一元一次不等式组的解集为x≤a;且关于y的分式方程+=1有正整数解,则所有满足条件的整数a的值之积是(A)
A.7 B.-14
C.28 D.-56
7.(2020·云南)若整数a使关于x的不等式组有且只有45个整数解,且使关于y的方程+=1的解为非正数,则a的值为(B)
A.-61或-58 B.-61或-59
C.-60或-59 D.-61或-60或-59
8.(2020·内江)若数a使关于x的分式方程+=3的解为非负数,且使关于y的不等式组的解集为y≤0,则符合条件的所有整数a的积为40.
9.若关于x的方程=2+无解,则m的值为(A)
A.-5 B.-8
C.-2 D.5
10.(2020·潍坊)若关于x的分式方程=+1有增根,则m=3.
11.【分类讨论思想】若关于x的方程=+1无解,则a的值是1或2.
专题4 分式方程的应用
1.(2020·威海)在“旅游示范公路”建设的过程中,工程队计划在海边某路段修建一条长1 200 m的步行道.由于采用新的施工方式,平均每天修建步行道的长度是计划的1.5倍,结果提前5天完成任务.求计划平均每天修建步行道的长度.
解:设计划平均每天修建步行道的长度为x m,则采用新的施工方式后平均每天修建步行道的长度为1.5x m,依题意,得
-=5,
解得x=80.
经检验,x=80是原方程的解,且符合题意.
答:计划平均每天修建步行道的长度为80 m.
2.某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
解:设升级前每小时生产x个零件,则升级后每小时生产(1+)x个零件.根据题意,得
-=+.
解得x=60.
经检验,x=60是原方程的解,且符合题意.
∴(1+)x=80.
答:软件升级后每小时生产80个零件.
3.(2020·益阳)新冠肺炎疫情暴发后,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有7人不能到厂生产.为了应对疫情,已复产的工人加班生产,由原来每天工作8小时增加到10小时,每小时完成的工作量不变.原来每天能生产防护服800套,现在每天能生产防护服650套.
(1)求原来生产防护服的工人有多少人?
(2)复工10天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时.公司决定将复工后生产的防护服14 500套捐献给某地,则至少还需要生产多少天才能完成任务?
解:(1)设原来生产防护服的工人有x人,由题意,得
=,
解得x=20.
经检验,x=20是原方程的解,且符合题意.
答:原来生产防护服的工人有20人.
(2)每人每小时生产=5(套)防护服.
设还需要生产y天才能完成任务.由题意,得
10×650+20×5×10y≥14 500,
解得y≥8.
答:至少还需要生产8天才能完成任务.
4.一项工程,甲、乙两公司合作,12天可以完成,共需付施工费102 000元;如果甲、乙两公司单独完成此项工程,乙公司所用的时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1 500元.
(1)甲、乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
解:(1)设甲公司单独完成此项工程需x天,则乙公司单独完成此项工程需1.5x天.根据题意,得
+=,解得x=20,
经检验,x=20是原方程的解,且符合题意.
则1.5x=30.
答:甲公司单独完成此项工程需20天,乙公司需30天.
(2)设甲公司每天的施工费为y元,则乙公司每天的施工费为(y-1 500)元,根据题意,得
12(y+y-1 500)=102 000,解得y=5 000.
甲公司单独完成此项工程所需的施工费为
20×5 000=100 000(元);
乙公司单独完成此项工程所需的施工费为
30×(5 000-1 500)=105 000(元).
∵100 000<105 000,
∴甲公司的施工费较少.
类型2 行程问题
5.(2020·泰州)近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线A为全程25 km的普通道路,路线B包含快速通道,全程30 km,走路线B比走路线A平均速度提高50%,时间节省6 min,求走路线B的平均速度.
解:设走路线A的平均速度为x km/h,则走路线B的平均速度为(1+50%)x km/h,
依题意,得
-=,
解得x=50.
经检验,x=50是原方程的解,且符合题意.
∴(1+50%)x=75.
答:走路线B的平均速度为75 km/h.
6.甲、乙两同学与学校的距离均为3 000米,甲同学先步行600米然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行的速度是乙骑自行车速度的,公交车速度是乙骑自行车速度的2倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
解:(1)设乙骑自行车的速度为x米/分钟,则甲步行的速度是x米/分钟,公交车的速度是2x米/分钟,根据题意,得
+=-2,
解得x=300.
经检验,x=300是原方程的解,且符合题意.
答:乙骑自行车的速度为300米/分钟.
(2)300×2=600(米).
答:当甲到达学校时,乙同学离学校还有600米.
类型3 购买与销售问题
7.(2019·泰安)端午节是我国的传统节日,人们素有吃粽子的习俗.某商场在端午节来临之际用3 000元购进A,B两种粽子1 100个,购买A种粽子与购买B种粽子的费用相同.已知A种粽子的单价是B种粽子单价的1.2倍.
(1)求A,B两种粽子的单价各是多少?
(2)若计划用不超过7 000元的资金再次购进A,B两种粽子共2 600个,已知A,B两种粽子的进价不变.求A种粽子最多能购进多少个?
解:(1)设B种粽子单价为x元/个,则A种粽子单价为1.2x元/个,根据题意,得
+=1 100,
解得x=2.5.
经检验,x=2.5是原方程的解,且符合题意,
∴1.2x=3.
答:A种粽子单价为3元/个,B种粽子单价为2.5元/个.
(2)设购进A种粽子m个,则购进B种粽子(2 600-m)个,依题意,得
3m+2.5(2 600-m)≤7 000,
解得m≤1 000.
答:A种粽子最多能购进1 000个.
8.(2020·黔西南)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,则今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1 500元和18 00元,计划B型车销售价格为2 400元,应如何组织进货才能使这批自行车销售获利最多?
解:(1)设去年A型车每辆售价x元,则今年售价每辆为(x-200)元,由题意,得
=,
解得x=2 000.
经检验,x=2 000是原方程的根,且符合题意.
答:去年A型车每辆售价为2 000元.
(2)设今年新进A型车a辆,则新进B型车(60-a)辆,获利y元,由题意,得
y=(2 000-200-1 500)a+(2 400-1 800)(60-a)
=-300a+36 000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60-a≤2a.
∴a≥20.
∵y=-300a+36 000.
∴k=-300<0.
∴y随a的增大而减小.
∴a=20时,y有最大值.
∴B型车的数量为60-20=40(辆).
答:当新进A型车20辆,B型车40辆时,能使这批自行车获利最多.
类型1 分式的运算
1.计算:
(1)(x+1)÷(1+); (2)-÷;
(3)÷(1-); (4)(-)3·(-)2÷(-)4;
(5)÷(x+); (6)(m+2+)·;
(7)(-a-1)÷; (8)1-(+)÷.
类型2 分式的化简求值
2.先化简,再求值:(1-)÷,其中a=+1.
3.先化简,再求值:(-)÷,其中x=+1,y=-1.
4. 已知y=,且x≠y,求(+)÷的值.
5.先化简:(-)÷,然后选择一个合适的x值代入求值.
6.化简求值:(-)÷,其中a2-a-1=0.
7.先化简,再求值:÷-,其中a,b满足(a-2)2+=0.
8.先化简,再求值:·(+1),其中x是不等式组的整数解.
专题2 解分式方程
1.解下列分式方程:
(1)(2020·镇江)=+1; (2)=-3;
(3)(2020·郴州)=+1; (4)=+1;
(5)-=1; (6)-1=;
(7)-=.
2.解分式方程:-=-.
专题3 由分式方程根的情况确定字母的取值范围
类型1 由特殊解确定字母的取值范围
由特殊解确定字母的取值范围的一般步骤如下:
(1)求出分式方程的根(用含有字母的式子表示);
(2)由分式方程的根为特殊解列出关于字母的不等式,并求出解集;
(3)由分式方程的解必须使分母不为0,列出关于字母的不等式,并求出解集;
(4)求(2)(3)中两个解集的公共部分即可.
1.关于x的分式方程=1的解为负数,则a的取值范围是( )
A.a>1 B.a<1
C.a<1且a≠-2 D.a>1且a≠2
2.(2020·齐齐哈尔)若关于x的分式方程=+5的解为正数,则m的取值范围为( )
A.m<-10
B.m≤-10
C.m≥-10且m≠-6
D.m>-10且m≠-6
3.(2020·黑龙江)已知关于x的分式方程-4=的解为非正数,则k的取值范围是( )
A.k≤-12 B.k≥-12
C.k>-12 D.k<-12
4.(2020·泸州)已知关于x的分式方程+2=-的解为非负数,则正整数m的所有个数为( )
A.3 B.4 C.5 D.6
5.已知关于x的分式方程-2=有一个正数解,则k的取值范围为 .
【易错提示】 求得的未知数不仅要满足所给出的范围,还要使分式的分母不为零,两个条件必须同时具备,缺一不可.
类型2 与不等式组的解集结合确定字母的取值
与不等式组的解集结合,确定字母的取值的一般步骤如下:
(1)由分式方程的根为特殊解确定字母的取值范围(方法同类型1);
(2)由不等式组的解集确定字母的取值范围;
(3)取(1)(2)中两个解集的公共部分即可.
6.(2020·重庆A卷)若关于x的一元一次不等式组的解集为x≤a;且关于y的分式方程+=1有正整数解,则所有满足条件的整数a的值之积是( )
A.7 B.-14
C.28 D.-56
7.(2020·云南)若整数a使关于x的不等式组有且只有45个整数解,且使关于y的方程+=1的解为非正数,则a的值为( )
A.-61或-58 B.-61或-59
C.-60或-59 D.-61或-60或-59
8.(2020·内江)若数a使关于x的分式方程+=3的解为非负数,且使关于y的不等式组的解集为y≤0,则符合条件的所有整数a的积为 .
类型3 由无解确定字母的取值
分式方程无解可能有两种情况:(1)去分母后化成的整式方程有解,但这个解使原方程的最简公分母为0,即是方程的增根;(2)去分母后化成的整式方程无解,即ax=b中,a=0且b≠0.
9.若关于x的方程=2+无解,则m的值为( )
A.-5 B.-8
C.-2 D.5
10.(2020·潍坊)若关于x的分式方程=+1有增根,则m= .
11.【分类讨论思想】若关于x的方程=+1无解,则a的值是 .
专题4 分式方程的应用
类型1 工程问题
1.(2020·威海)在“旅游示范公路”建设的过程中,工程队计划在海边某路段修建一条长1 200 m的步行道.由于采用新的施工方式,平均每天修建步行道的长度是计划的1.5倍,结果提前5天完成任务.求计划平均每天修建步行道的长度.
2.某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
3.(2020·益阳)新冠肺炎疫情暴发后,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有7人不能到厂生产.为了应对疫情,已复产的工人加班生产,由原来每天工作8小时增加到10小时,每小时完成的工作量不变.原来每天能生产防护服800套,现在每天能生产防护服650套.
(1)求原来生产防护服的工人有多少人?
(2)复工10天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时.公司决定将复工后生产的防护服14 500套捐献给某地,则至少还需要生产多少天才能完成任务?
4.一项工程,甲、乙两公司合作,12天可以完成,共需付施工费102 000元;如果甲、乙两公司单独完成此项工程,乙公司所用的时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1 500元.
(1)甲、乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
类型2 行程问题
5.(2020·泰州)近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线A为全程25 km的普通道路,路线B包含快速通道,全程30 km,走路线B比走路线A平均速度提高50%,时间节省6 min,求走路线B的平均速度.
6.甲、乙两同学与学校的距离均为3 000米,甲同学先步行600米然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行的速度是乙骑自行车速度的,公交车速度是乙骑自行车速度的2倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
类型3 购买与销售问题
7.(2019·泰安)端午节是我国的传统节日,人们素有吃粽子的习俗.某商场在端午节来临之际用3 000元购进A,B两种粽子1 100个,购买A种粽子与购买B种粽子的费用相同.已知A种粽子的单价是B种粽子单价的1.2倍.
(1)求A,B两种粽子的单价各是多少?
(2)若计划用不超过7 000元的资金再次购进A,B两种粽子共2 600个,已知A,B两种粽子的进价不变.求A种粽子最多能购进多少个?
8.(2020·黔西南)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,则今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1 500元和18 00元,计划B型车销售价格为2 400元,应如何组织进货才能使这批自行车销售获利最多?
参考答案:
专题1 分式的运算及化简求值
类型1 分式的运算
1.计算:
(1)(x+1)÷(1+);
解:原式=(x+1)÷
=(x+1)·
=x.
(2)-÷;
解:原式=-·
=-
=.
(3)÷(1-);
解:原式=÷
=·
=2.
(4)(-)3·(-)2÷(-)4;
解:原式=-·÷
=-a2b3c·
=-.
(5)÷(x+);
解:原式=÷(+)
=÷
=·
=.
(6)(m+2+)·;
解:原式=·
=·
=m+1.
(7)(-a-1)÷;
解:原式=(-)÷
=·
=.
(8)1-(+)÷.
解:原式=1-·
=1-
=
=.
类型2 分式的化简求值
2.先化简,再求值:(1-)÷,其中a=+1.
解:原式=·
=a-1.
当a=+1时,原式=+1-1=.
3.先化简,再求值:(-)÷,其中x=+1,y=-1.
解:原式=[-]÷
=·
=.
当x=+1,y=-1时,原式==2-.
4. 已知y=,且x≠y,求(+)÷的值.
解:原式=÷
=·
=.
∵y=,∴xy=2.
∴原式==1.
5.先化简:(-)÷,然后选择一个合适的x值代入求值.
解:原式=[-]·
=·
=.
要使分式有意义,则x(x-2)≠0,4-x≠0,
∴x≠0,2,4.
当x=1时,原工==-1.(答案不唯一,x不取0,2,4即可)
6.化简求值:(-)÷,其中a2-a-1=0.
解:原式=·
=·
=.
∵a2-a-1=0.∴a2=a+1.
∴原式==1.
7.先化简,再求值:÷-,其中a,b满足(a-2)2+=0.
解:原式=·-
=-
=-.
∵a,b满足(a-2)2+=0,
∴a-2=0,b+1=0.
∴a=2,b=-1.
∴原式=-=-1.
8.先化简,再求值:·(+1),其中x是不等式组的整数解.
解:原式=·
=
=.
解不等式组得-1≤x<1.
∵x是不等式组的整数解,
∴x=-1,0.
∵当x=-1时,原分式无意义,
∴x=0.
当x=0时,原式==-.
专题2 解分式方程
1.解下列分式方程:
(1)(2020·镇江)=+1;
解:去分母,得2x=1+x+3,
解得x=4.
检验:当x=4时,x+3≠0.
所以原方程的解是x=4.
(2)=-3;
解:方程两边同乘(x-2),得1=x-1-3x+6.
解得x=2.
检验:当x=2时,x-2=0,
所以x=2是原方程的增根,原方程无解.
(3)(2020·郴州)=+1;
解:方程两边都乘(x-1)(x+1),得
x(x+1)=4+(x-1)(x+1),
解得x=3.
检验:当x=3时,(x-1)(x+1)=8≠0.
故x=3是原方程的解.
(4)=+1;
解:去分母,得3x=2x+3x+3.
解得x=-.
检验:当x=-时,3(x+1)≠0,
所以x=-为原方程的解.
(5)-=1;
解:去分母,得(x+3)2-4(x-3)=(x-3)(x+3).
解得x=-15.
检验:当x=-15时,(x-3)(x+3)≠0,
所以原分式方程的解为x=-15.
(6)-1=;
解:去分母,得x(x+2)-(x-1)(x+2)=3.
去括号,得x2+2x-x2-2x+x+2=3.
解得x=1.
检验:当x=1时,(x-1)(x+2)=0,
所以x=1是原方程的增根,原方程无解.
(7)-=.
解:方程两边同乘x(x-2),得
(x-2)(2x+2)-x(x+2)=x2-2.
解得x=-.
检验:当x=-时,x(x-2)≠0,
所以x=-是原方程的解.
2.解分式方程:-=-.
解:两边通分,得
=,
=,
去分母,整理,得6x=36,
解得x=6.
检验:当x=6时,(x-4)(x-5)(x-7)(x-8)≠0,
所以x=6是原分式方程的解.
专题3 由分式方程根的情况确定字母的取值范围
1.关于x的分式方程=1的解为负数,则a的取值范围是(D)
A.a>1 B.a<1
C.a<1且a≠-2 D.a>1且a≠2
2.(2020·齐齐哈尔)若关于x的分式方程=+5的解为正数,则m的取值范围为(D)
A.m<-10
B.m≤-10
C.m≥-10且m≠-6
D.m>-10且m≠-6
3.(2020·黑龙江)已知关于x的分式方程-4=的解为非正数,则k的取值范围是(A)
A.k≤-12 B.k≥-12
C.k>-12 D.k<-12
4.(2020·泸州)已知关于x的分式方程+2=-的解为非负数,则正整数m的所有个数为(B)
A.3 B.4 C.5 D.6
5.已知关于x的分式方程-2=有一个正数解,则k的取值范围为k<6且k≠3.
6.(2020·重庆A卷)若关于x的一元一次不等式组的解集为x≤a;且关于y的分式方程+=1有正整数解,则所有满足条件的整数a的值之积是(A)
A.7 B.-14
C.28 D.-56
7.(2020·云南)若整数a使关于x的不等式组有且只有45个整数解,且使关于y的方程+=1的解为非正数,则a的值为(B)
A.-61或-58 B.-61或-59
C.-60或-59 D.-61或-60或-59
8.(2020·内江)若数a使关于x的分式方程+=3的解为非负数,且使关于y的不等式组的解集为y≤0,则符合条件的所有整数a的积为40.
9.若关于x的方程=2+无解,则m的值为(A)
A.-5 B.-8
C.-2 D.5
10.(2020·潍坊)若关于x的分式方程=+1有增根,则m=3.
11.【分类讨论思想】若关于x的方程=+1无解,则a的值是1或2.
专题4 分式方程的应用
1.(2020·威海)在“旅游示范公路”建设的过程中,工程队计划在海边某路段修建一条长1 200 m的步行道.由于采用新的施工方式,平均每天修建步行道的长度是计划的1.5倍,结果提前5天完成任务.求计划平均每天修建步行道的长度.
解:设计划平均每天修建步行道的长度为x m,则采用新的施工方式后平均每天修建步行道的长度为1.5x m,依题意,得
-=5,
解得x=80.
经检验,x=80是原方程的解,且符合题意.
答:计划平均每天修建步行道的长度为80 m.
2.某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
解:设升级前每小时生产x个零件,则升级后每小时生产(1+)x个零件.根据题意,得
-=+.
解得x=60.
经检验,x=60是原方程的解,且符合题意.
∴(1+)x=80.
答:软件升级后每小时生产80个零件.
3.(2020·益阳)新冠肺炎疫情暴发后,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有7人不能到厂生产.为了应对疫情,已复产的工人加班生产,由原来每天工作8小时增加到10小时,每小时完成的工作量不变.原来每天能生产防护服800套,现在每天能生产防护服650套.
(1)求原来生产防护服的工人有多少人?
(2)复工10天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时.公司决定将复工后生产的防护服14 500套捐献给某地,则至少还需要生产多少天才能完成任务?
解:(1)设原来生产防护服的工人有x人,由题意,得
=,
解得x=20.
经检验,x=20是原方程的解,且符合题意.
答:原来生产防护服的工人有20人.
(2)每人每小时生产=5(套)防护服.
设还需要生产y天才能完成任务.由题意,得
10×650+20×5×10y≥14 500,
解得y≥8.
答:至少还需要生产8天才能完成任务.
4.一项工程,甲、乙两公司合作,12天可以完成,共需付施工费102 000元;如果甲、乙两公司单独完成此项工程,乙公司所用的时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1 500元.
(1)甲、乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
解:(1)设甲公司单独完成此项工程需x天,则乙公司单独完成此项工程需1.5x天.根据题意,得
+=,解得x=20,
经检验,x=20是原方程的解,且符合题意.
则1.5x=30.
答:甲公司单独完成此项工程需20天,乙公司需30天.
(2)设甲公司每天的施工费为y元,则乙公司每天的施工费为(y-1 500)元,根据题意,得
12(y+y-1 500)=102 000,解得y=5 000.
甲公司单独完成此项工程所需的施工费为
20×5 000=100 000(元);
乙公司单独完成此项工程所需的施工费为
30×(5 000-1 500)=105 000(元).
∵100 000<105 000,
∴甲公司的施工费较少.
类型2 行程问题
5.(2020·泰州)近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线A为全程25 km的普通道路,路线B包含快速通道,全程30 km,走路线B比走路线A平均速度提高50%,时间节省6 min,求走路线B的平均速度.
解:设走路线A的平均速度为x km/h,则走路线B的平均速度为(1+50%)x km/h,
依题意,得
-=,
解得x=50.
经检验,x=50是原方程的解,且符合题意.
∴(1+50%)x=75.
答:走路线B的平均速度为75 km/h.
6.甲、乙两同学与学校的距离均为3 000米,甲同学先步行600米然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行的速度是乙骑自行车速度的,公交车速度是乙骑自行车速度的2倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
解:(1)设乙骑自行车的速度为x米/分钟,则甲步行的速度是x米/分钟,公交车的速度是2x米/分钟,根据题意,得
+=-2,
解得x=300.
经检验,x=300是原方程的解,且符合题意.
答:乙骑自行车的速度为300米/分钟.
(2)300×2=600(米).
答:当甲到达学校时,乙同学离学校还有600米.
类型3 购买与销售问题
7.(2019·泰安)端午节是我国的传统节日,人们素有吃粽子的习俗.某商场在端午节来临之际用3 000元购进A,B两种粽子1 100个,购买A种粽子与购买B种粽子的费用相同.已知A种粽子的单价是B种粽子单价的1.2倍.
(1)求A,B两种粽子的单价各是多少?
(2)若计划用不超过7 000元的资金再次购进A,B两种粽子共2 600个,已知A,B两种粽子的进价不变.求A种粽子最多能购进多少个?
解:(1)设B种粽子单价为x元/个,则A种粽子单价为1.2x元/个,根据题意,得
+=1 100,
解得x=2.5.
经检验,x=2.5是原方程的解,且符合题意,
∴1.2x=3.
答:A种粽子单价为3元/个,B种粽子单价为2.5元/个.
(2)设购进A种粽子m个,则购进B种粽子(2 600-m)个,依题意,得
3m+2.5(2 600-m)≤7 000,
解得m≤1 000.
答:A种粽子最多能购进1 000个.
8.(2020·黔西南)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,则今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1 500元和18 00元,计划B型车销售价格为2 400元,应如何组织进货才能使这批自行车销售获利最多?
解:(1)设去年A型车每辆售价x元,则今年售价每辆为(x-200)元,由题意,得
=,
解得x=2 000.
经检验,x=2 000是原方程的根,且符合题意.
答:去年A型车每辆售价为2 000元.
(2)设今年新进A型车a辆,则新进B型车(60-a)辆,获利y元,由题意,得
y=(2 000-200-1 500)a+(2 400-1 800)(60-a)
=-300a+36 000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60-a≤2a.
∴a≥20.
∵y=-300a+36 000.
∴k=-300<0.
∴y随a的增大而减小.
∴a=20时,y有最大值.
∴B型车的数量为60-20=40(辆).
答:当新进A型车20辆,B型车40辆时,能使这批自行车获利最多.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
