【备考2021】高中物理模型问题专项突破 07板块相对运动模型 课件(19张ppt)
文档属性
| 名称 | 【备考2021】高中物理模型问题专项突破 07板块相对运动模型 课件(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 340.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览






文档简介
模型07 板块相对运动模型
2021年高中模型问题专项突破
模型概述
01
两种类型
此类问题涉及两个物体、多个运动过程,并且物体间还存在相对运动,所以应准确求出各物体在各运动过程的加速度(注意两过程的连接处加速度可能突变),找出物体之间的位移(路程)关系或速度关系是解题的突破口。求解中更应注意联系两个过程的纽带,每一个过程的末速度是下一个过程的初速度。
类型图示
规律分析
木板B带动物块A,物块恰好不从木板上掉下的临界条件是物块恰好滑到木板左端时二者速度相等,则位移关系为xB=xA+L
物块A带动木板B,物块恰好不从木板上掉下的临界条件是物块恰好滑到木板右端时二者速度相等,则位移关系为xB+L=xA
02
精讲精练
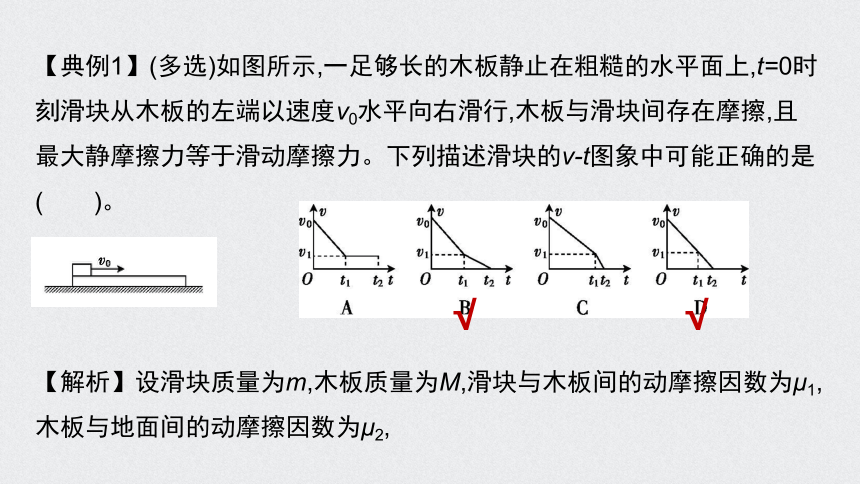
【典例1】(多选)如图所示,一足够长的木板静止在粗糙的水平面上,t=0时刻滑块从木板的左端以速度v0水平向右滑行,木板与滑块间存在摩擦,且最大静摩擦力等于滑动摩擦力。下列描述滑块的v-t图象中可能正确的是( )。
【解析】设滑块质量为m,木板质量为M,滑块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数为μ2,
√
√
√
若μ1mg<μ2(M+m)g,则滑块滑上木板后向右做匀减速运动,加速度a1=μ1g,木板静止,D项可能;
若μ1mg>μ2(M+m)g,则滑块滑上木板后向右做匀减速运动,加速度a1=μ1g,木板向右做匀加速运动,当二者速度相等后,一起以a2=μ2g的加速度匀减速到停止,且a1>a2,B项可能。
【变式训练1 】 质量M=4 kg、长为2l=4 m的木板放在光滑水平地面上,以木板中点为界,左边和右边的动摩擦因数不同。一个质量m=1 kg的滑块(可视为质点)放在木板的左端,如图甲所示。在t=0时刻对滑块施加一个水平向右的恒力F,使滑块和木板均由静止开始运动,t1=2 s时滑块恰好到达木板中点,滑块运动的x1-t图象如图乙所示。重力加速度取g=10 m/s2。 (1)求滑块与木板左边的动摩擦因数μ1和恒力F的大小。
(2)若滑块与木板右边之间的动摩擦因数μ2=0.1,2 s末撤去恒力F,则滑块能否从木板上滑落下来?若能,求分离时滑块的速度大小。若不能,则滑块将停在离木板右端多远处?
【答案】(1)0.4 6N (2)不能 0.4m
【解析】(1)滑块和木板均做初速度为零的匀加速直线运动,设滑块的加速度大小为a1,木板的加速度大小为a2,则t1=2s时木板的位移x2= a2
滑块的位移x1=4m
由牛顿第二定律得a2=
由位移关系得x1-x2=l
联立解得μ1=0.4
滑块位移x1= a1
恒力F=ma1+μ1mg
联立解得F=6N。
(2)设滑块到达木板中点时,滑块的速度为v1,木板的速度为v2,滑块滑过中点后做匀减速运动,木板以另一加速度做匀加速运动,此时滑块和木板的加速度大小分别为
a1'= μ2g, a2'=
设滑块与木板从t1时刻开始到速度相等时的运动时间为t2,则v2=a2t1,v1=a1t1,v1-a1't2=v2+a2't2
解得t2=1.6s
在此时间内,滑块位移x1'=v1t2- a1'
木板的位移x2'=v2t2+ a2'
滑块相对木板运动的位移Δx=x1'-x2'
联立解得Δx=1.6m<2m
因此滑块没有从木板上滑落,滑块与木板相对静止时到木板右端的距离d=l-Δx=0.4m。
【变式训练2】如图甲所示,有一倾角θ=30°的光滑固定斜面,在与斜面底端相接的水平面上放一质量为M的木板。开始时质量m=1 kg 的滑块在水平向左的力F作用下静止在斜面上,现将力F变为水平向右,当滑块滑到木板上时撤去力F,滑块滑上木板的过程不考虑能量损失。此后滑块和木板在水平面上运动的v-t图象如图乙所示,g=10 m/s2。求:
(1)水平作用力F的大小。
(2)滑块开始下滑时的高度。
(3)木板的质量。
【答案】(1) N (2)2.5m (3)1.5kg
【解析】(1)滑块受力如图丙所示,根据平衡条件,有mgsinθ=Fcosθ,
解得F= N。
(2)当力F变为水平向右之后,由牛顿第二定律,有mgsinθ+Fcosθ=ma
解得a=10m/s2
根据题意,由题图乙可知,滑块滑到木板上的初速度v=10m/s
滑块下滑的位移x= ,解得x=5m
故滑块下滑的高度h=xsin30°=2.5m。
(3)由题图乙可知,滑块到达木板上后,滑块和木板起初相对滑动,当达到共同速度后一起做匀减速运动,两者共同减速时加速度a1=1m/s2,相对滑动时,木板的加速度a2=1m/s2,滑块的加速度大小a3=4m/s2
设木板与地面间的动摩擦因数为μ1,滑块与木板间的动摩擦因数为μ2,对它们整体受力分析,有a1=μ1g,解得μ1=0.1
0~2s内分别对木板和滑块受力分析,对木板有μ2mg-μ1(M+m)g=Ma2
对滑块有μ2mg=ma3
联立解得M=1.5kg。
【变式训练3】 传送带与平板紧靠在一起,且上表面在同一水平面内,两者长度分别为L1=2.5 m、L2=2 m。传送带始终保持以速度v匀速运动。现将一滑块(可视为质点)轻放到传送带的左端,然后平稳地滑上平板。已知滑块与传送带间的动摩擦因数μ=0.5,滑块与平板、平板与
支持面间的动摩擦因数分别为μ1=0.3、μ2=0.1,滑块、平板的质量均为m=2 kg,重力加速度g取10 m/s2。
(1)若滑块恰好不从平板上掉下,求v的大小。
(2)若v=6 m/s,求滑块离开平板时的速度大小。
【答案】(1)4m/s (2)3.5m/s
1
2
3
4
5
6
【解析】(1)滑块在平板上做匀减速运动,加速度大小
a1= =3m/s2
由于μ1mg>2μ2mg,故平板做匀加速运动,加速度大小
a2= =1m/s2
设滑块滑至平板右端用时为t,共同速度为v',平板位移为x,
对滑块有v'=v-a1t
L2+x=vt- a1t2
对平板有v'=a2t,x= a2t2
联立解得t=1s,v=4m/s
7
1
2
3
4
5
6
滑块在传送带上的加速度a3= =5m/s2
若滑块在传送带上一直加速,则获得的速度
v1= =5m/s>4m/s
只有v=4m/s符合题意。
(2)v1=5m/s<6m/s,即滑块滑上平板的速度为5m/s
设滑块在平板上运动的时间为t',离开平板时的速度为v″,平板位移为x'
则v″=v1-a1t',L2+x'=v1t'- a1t'2
x'= a2t'2
联立解得t1'= s,t2'=2s(t2'>t,不合题意,舍去)
将t'= s代入v″=v1-a1t'得v″=3.5m/s。
7
【变式训练4】如图所示,倾角α=30°的足够长的光滑斜面固定在水平面上,斜面上放一长L=1.8 m,质量M=3 kg的薄木板,木板的最上端叠放一质量m=1 kg的小物块,物块与木板间的动摩擦因数μ= 。对木板施加沿斜面向上的恒力F,使木板沿斜面由静止开始向上做匀加速直线运动,假设物块与木板间的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2。
(1)为使物块不滑离木板,求力F应满足的条件。
(2)若F=37.5 N,物块能否滑离木板?若不能,请说明理由;若能,求出物块滑离木板所用的时间及滑离木板后沿斜面上升的最大距离。
【答案】(1)20N1
2
3
4
5
6
7
【解析】(1)若整体恰好静止,则F=(M+m)gsinα=20N
因要拉动木板,则F>20N
若整体一起向上做匀加速直线运动,对物块和木板,由牛顿第二定律得
F-(M+m)gsinα=(M+m)a
对物块有f-mgsinα=ma
其中f≤μmgcosα
代入数据解得F≤30N
向上加速的过程中为使物块不滑离木板,
力F应满足的条件为20N(2)当F=37.5N>30N时,物块能滑离木板,由牛顿第二定律,
对木板有F-μmgcosα-Mgsinα=Ma1
对物块有μmgcosα-mgsinα=ma2
设物块滑离木板所用的时间为t,由运动学公式得
a1t2- a2t2=L
解得t=1.2s
物块滑离木板时的速度v=a2t
滑离后沿斜面上升的最大距离,满足-2gssinα=0-v2
解得s=0.9m。
2021年高中模型问题专项突破
模型概述
01
两种类型
此类问题涉及两个物体、多个运动过程,并且物体间还存在相对运动,所以应准确求出各物体在各运动过程的加速度(注意两过程的连接处加速度可能突变),找出物体之间的位移(路程)关系或速度关系是解题的突破口。求解中更应注意联系两个过程的纽带,每一个过程的末速度是下一个过程的初速度。
类型图示
规律分析
木板B带动物块A,物块恰好不从木板上掉下的临界条件是物块恰好滑到木板左端时二者速度相等,则位移关系为xB=xA+L
物块A带动木板B,物块恰好不从木板上掉下的临界条件是物块恰好滑到木板右端时二者速度相等,则位移关系为xB+L=xA
02
精讲精练
【典例1】(多选)如图所示,一足够长的木板静止在粗糙的水平面上,t=0时刻滑块从木板的左端以速度v0水平向右滑行,木板与滑块间存在摩擦,且最大静摩擦力等于滑动摩擦力。下列描述滑块的v-t图象中可能正确的是( )。
【解析】设滑块质量为m,木板质量为M,滑块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数为μ2,
√
√
√
若μ1mg<μ2(M+m)g,则滑块滑上木板后向右做匀减速运动,加速度a1=μ1g,木板静止,D项可能;
若μ1mg>μ2(M+m)g,则滑块滑上木板后向右做匀减速运动,加速度a1=μ1g,木板向右做匀加速运动,当二者速度相等后,一起以a2=μ2g的加速度匀减速到停止,且a1>a2,B项可能。
【变式训练1 】 质量M=4 kg、长为2l=4 m的木板放在光滑水平地面上,以木板中点为界,左边和右边的动摩擦因数不同。一个质量m=1 kg的滑块(可视为质点)放在木板的左端,如图甲所示。在t=0时刻对滑块施加一个水平向右的恒力F,使滑块和木板均由静止开始运动,t1=2 s时滑块恰好到达木板中点,滑块运动的x1-t图象如图乙所示。重力加速度取g=10 m/s2。 (1)求滑块与木板左边的动摩擦因数μ1和恒力F的大小。
(2)若滑块与木板右边之间的动摩擦因数μ2=0.1,2 s末撤去恒力F,则滑块能否从木板上滑落下来?若能,求分离时滑块的速度大小。若不能,则滑块将停在离木板右端多远处?
【答案】(1)0.4 6N (2)不能 0.4m
【解析】(1)滑块和木板均做初速度为零的匀加速直线运动,设滑块的加速度大小为a1,木板的加速度大小为a2,则t1=2s时木板的位移x2= a2
滑块的位移x1=4m
由牛顿第二定律得a2=
由位移关系得x1-x2=l
联立解得μ1=0.4
滑块位移x1= a1
恒力F=ma1+μ1mg
联立解得F=6N。
(2)设滑块到达木板中点时,滑块的速度为v1,木板的速度为v2,滑块滑过中点后做匀减速运动,木板以另一加速度做匀加速运动,此时滑块和木板的加速度大小分别为
a1'= μ2g, a2'=
设滑块与木板从t1时刻开始到速度相等时的运动时间为t2,则v2=a2t1,v1=a1t1,v1-a1't2=v2+a2't2
解得t2=1.6s
在此时间内,滑块位移x1'=v1t2- a1'
木板的位移x2'=v2t2+ a2'
滑块相对木板运动的位移Δx=x1'-x2'
联立解得Δx=1.6m<2m
因此滑块没有从木板上滑落,滑块与木板相对静止时到木板右端的距离d=l-Δx=0.4m。
【变式训练2】如图甲所示,有一倾角θ=30°的光滑固定斜面,在与斜面底端相接的水平面上放一质量为M的木板。开始时质量m=1 kg 的滑块在水平向左的力F作用下静止在斜面上,现将力F变为水平向右,当滑块滑到木板上时撤去力F,滑块滑上木板的过程不考虑能量损失。此后滑块和木板在水平面上运动的v-t图象如图乙所示,g=10 m/s2。求:
(1)水平作用力F的大小。
(2)滑块开始下滑时的高度。
(3)木板的质量。
【答案】(1) N (2)2.5m (3)1.5kg
【解析】(1)滑块受力如图丙所示,根据平衡条件,有mgsinθ=Fcosθ,
解得F= N。
(2)当力F变为水平向右之后,由牛顿第二定律,有mgsinθ+Fcosθ=ma
解得a=10m/s2
根据题意,由题图乙可知,滑块滑到木板上的初速度v=10m/s
滑块下滑的位移x= ,解得x=5m
故滑块下滑的高度h=xsin30°=2.5m。
(3)由题图乙可知,滑块到达木板上后,滑块和木板起初相对滑动,当达到共同速度后一起做匀减速运动,两者共同减速时加速度a1=1m/s2,相对滑动时,木板的加速度a2=1m/s2,滑块的加速度大小a3=4m/s2
设木板与地面间的动摩擦因数为μ1,滑块与木板间的动摩擦因数为μ2,对它们整体受力分析,有a1=μ1g,解得μ1=0.1
0~2s内分别对木板和滑块受力分析,对木板有μ2mg-μ1(M+m)g=Ma2
对滑块有μ2mg=ma3
联立解得M=1.5kg。
【变式训练3】 传送带与平板紧靠在一起,且上表面在同一水平面内,两者长度分别为L1=2.5 m、L2=2 m。传送带始终保持以速度v匀速运动。现将一滑块(可视为质点)轻放到传送带的左端,然后平稳地滑上平板。已知滑块与传送带间的动摩擦因数μ=0.5,滑块与平板、平板与
支持面间的动摩擦因数分别为μ1=0.3、μ2=0.1,滑块、平板的质量均为m=2 kg,重力加速度g取10 m/s2。
(1)若滑块恰好不从平板上掉下,求v的大小。
(2)若v=6 m/s,求滑块离开平板时的速度大小。
【答案】(1)4m/s (2)3.5m/s
1
2
3
4
5
6
【解析】(1)滑块在平板上做匀减速运动,加速度大小
a1= =3m/s2
由于μ1mg>2μ2mg,故平板做匀加速运动,加速度大小
a2= =1m/s2
设滑块滑至平板右端用时为t,共同速度为v',平板位移为x,
对滑块有v'=v-a1t
L2+x=vt- a1t2
对平板有v'=a2t,x= a2t2
联立解得t=1s,v=4m/s
7
1
2
3
4
5
6
滑块在传送带上的加速度a3= =5m/s2
若滑块在传送带上一直加速,则获得的速度
v1= =5m/s>4m/s
只有v=4m/s符合题意。
(2)v1=5m/s<6m/s,即滑块滑上平板的速度为5m/s
设滑块在平板上运动的时间为t',离开平板时的速度为v″,平板位移为x'
则v″=v1-a1t',L2+x'=v1t'- a1t'2
x'= a2t'2
联立解得t1'= s,t2'=2s(t2'>t,不合题意,舍去)
将t'= s代入v″=v1-a1t'得v″=3.5m/s。
7
【变式训练4】如图所示,倾角α=30°的足够长的光滑斜面固定在水平面上,斜面上放一长L=1.8 m,质量M=3 kg的薄木板,木板的最上端叠放一质量m=1 kg的小物块,物块与木板间的动摩擦因数μ= 。对木板施加沿斜面向上的恒力F,使木板沿斜面由静止开始向上做匀加速直线运动,假设物块与木板间的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2。
(1)为使物块不滑离木板,求力F应满足的条件。
(2)若F=37.5 N,物块能否滑离木板?若不能,请说明理由;若能,求出物块滑离木板所用的时间及滑离木板后沿斜面上升的最大距离。
【答案】(1)20N
2
3
4
5
6
7
【解析】(1)若整体恰好静止,则F=(M+m)gsinα=20N
因要拉动木板,则F>20N
若整体一起向上做匀加速直线运动,对物块和木板,由牛顿第二定律得
F-(M+m)gsinα=(M+m)a
对物块有f-mgsinα=ma
其中f≤μmgcosα
代入数据解得F≤30N
向上加速的过程中为使物块不滑离木板,
力F应满足的条件为20N
对木板有F-μmgcosα-Mgsinα=Ma1
对物块有μmgcosα-mgsinα=ma2
设物块滑离木板所用的时间为t,由运动学公式得
a1t2- a2t2=L
解得t=1.2s
物块滑离木板时的速度v=a2t
滑离后沿斜面上升的最大距离,满足-2gssinα=0-v2
解得s=0.9m。
同课章节目录
