【备考2021】高中物理模型问题专项突破 11竖直平面上的圆周运动 课件(17张ppt)
文档属性
| 名称 | 【备考2021】高中物理模型问题专项突破 11竖直平面上的圆周运动 课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 349.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览






文档简介
模型11 竖直平面上的圆周运动
2021年高中模型问题专项突破
模型概述
01
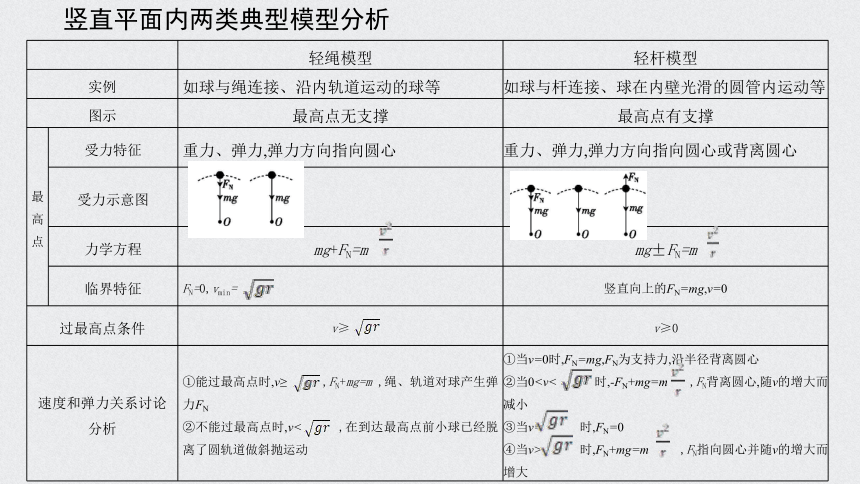
竖直平面内两类典型模型分析
轻绳模型
轻杆模型
实例
如球与绳连接、沿内轨道运动的球等
如球与杆连接、球在内壁光滑的圆管内运动等
图示
最高点无支撑
最高点有支撑
最
高
点
受力特征
重力、弹力,弹力方向指向圆心
重力、弹力,弹力方向指向圆心或背离圆心
受力示意图
力学方程
mg+FN=m
mg±FN=m
临界特征
FN=0,vmin=
竖直向上的FN=mg,v=0
过最高点条件
v≥
v≥0
速度和弹力关系讨论
分析
①能过最高点时,v≥ ,FN+mg=m ,绳、轨道对球产生弹力FN
②不能过最高点时,v< ,在到达最高点前小球已经脱离了圆轨道做斜抛运动
①当v=0时,FN=mg,FN为支持力,沿半径背离圆心
②当0③当v= 时,FN=0
④当v> 时,FN+mg=m ,FN指向圆心并随v的增大而增大
02
精讲精练
【典例1】“水流星”是一个经典的杂技表演项目,杂技演员将装水的杯子(可视为质点)用细绳系着让杯子在竖直平面内做圆周运动。杯子到最高点时杯口向下,水也不会从杯中流出,如图所示。若杯子质量为m,所装水的质量为M,杯子运动到圆周的最高点时,水对杯底刚好无压力,重力加速度为g,则杯子运动到圆周最高点时,杂技演员对细绳的拉力大小为( )。
A.0 B.mg C.Mg D.(M+m)g
【解析】杯子到最高点时,由于水刚好没有流出,则杯底对水的作用力为零,设这时杯子的速度大小为v,对水研究有Mg=M ,对杯子和水整体研究,设绳的拉力为F,则F+(M+m)g=(M+m) ,解得F=0,A项正确。
√
【变式训练1】如图3所示为模拟过山车的实验装置,小球从左侧的最高点释放后能够通过竖直圆轨道而到达右侧.若竖直圆轨道的半径为R,要使小球能顺利通过竖直圆轨道,则小球通过竖直圆轨道的最高点时的角速度最小为( )
A. B.2 C. D.
【解析】小球能通过竖直圆轨道的最高点的临界状态为重力提供向心力,即mg=mω2R,解得ω= ,选项C正确.
√
【变式训练2】 一细绳与水桶相连,水桶中装有水,水桶与细绳一起在竖直平面内做圆周运动,如图2所示,水的质量m=0.5 kg,水的重心到转轴的距离r=50 cm.(g取10 m/s2)
(1)若在最高点水不流出来,求桶最小速率;(结果保留三位有效数字)
(2)若在最高点水桶的速率v=3 m/s,求水对桶底的压力大小.
【答案】(1)2.24 m/s (2)4 N
【解析】(1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,此时桶的速率最小.
此时有:mg=m ,
则所求的最小速率为:
v0= ≈2.24 m/s.
(2)此时桶底对水有一向下的压力,设为FN,则由牛顿第二定律有:
FN+mg=m ,
代入数据可得:FN=4 N.
由牛顿第三定律,水对桶底的压力:
FN′=4 N.
【典例2】长度为0.5 m的轻杆OA绕O点在竖直平面内做圆周运动,A端连着一个质量m=2 kg的小球.求在下述的两种情况下,通过最高点时小球对杆的作用力的大小和方向.(g取10 m/s2)
(1)杆做匀速圆周运动的转速为2.0 r/s;
(2)杆做匀速圆周运动的转速为0.5 r/s.
【答案】(1)小球对杆的拉力为138 N,方向竖直向上
【解析】 小球在最高点的受力如图所示:
(1)杆的转速为2.0 r/s时,ω=2π·n=4π rad/s
由牛顿第二定律得F+mg=mLω2
故小球所受杆的作用力
F=mLω2-mg=2×(0.5×42×π2-10)N≈138 N
即杆对小球提供了138 N的拉力.
由牛顿第三定律知小球对杆的拉力大小为138 N,方向竖直向上.
(2)杆的转速为0.5 r/s时,ω′=2π·n=π rad/s
同理可得小球所受杆的作用力
F=mLω′2-mg=2×(0.5×π2-10)N≈-10 N.
力F为负值表示它的方向与受力分析中所假设的方向相反,故小球对杆的压力大小为10 N,方向竖直向下.
【变式训练3】 (多选)如图所示,一个固定在竖直平面上的光滑圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,下列说法中正确的是( )
A.小球通过管道最低点时,小球对管道的压力向下
B.小球通过管道最低点时,小球对管道的压力向上
C.小球通过管道最高点时,小球对管道的压力可能向上
D.小球通过管道最高点时,小球对管道可能无压力
√
【解析】设管道的半径为R,小球的质量为m,小球通过最低点时速度大小为v1,根据牛顿第二定律:N-mg=m 可知小球所受合力向上,则管道对小球的支持力向上,则小球对管道的压力向下,故A正确,B错误;最高点时速度大小为v2,根据牛顿第二定律:mg-N=m ,当v2= 时,N=0,说明管道对小球无压力;当v2> 时,N<0,说明管道对小球的作用力向下,则小球对管道的压力向上,故C、D正确.所以A、C、D正确,B错误.
【变式训练4】(多选)如图所示,半径为R的光滑细圆环轨道被固定在竖直平面上,轨道正上方和正下方分别有质量为2m和m的静止小球A、B,它们由长为2R的轻杆固定连接,圆环轨道内壁开有环形小槽,可使细杆无摩擦、无障碍地绕其中心点转动。今对上方小球A施加微小扰动。两球开始运动后,下列说法正确的是( )。
A.轻杆转到水平位置时,两球的线速度大小相等
B.轻杆转到竖直位置时,两球的加速度大小不相等
C.运动过程中,A球速度的最大值为
D.当A球运动到最低点时,两小球对轨道作用力的合力大小为 mg
√
√
√
【解析】两球做圆周运动,在任意位置角速度相等,则线速度和向心加速度大小相等,A项正确,B项错误;A、B两球组成的系统机械能守恒,当系统重力势能最小(A为最低点)时,线速度最大,则mg·2R= ×3mv2,最大速度v= ,C项正确;A在最低点时,分别对A、B受力分析,有FNA-2mg=2m ,FNB+mg=m ,则FNA-FNB= ,D项正确。
1
2
3
4
5
6
【变式训练5】(多选)如图甲所示,我国男子体操运动员在里约奥运会上个人全能中完成“单臂大回环”的高难度动作:用一只手抓住单杠,伸展身体,以单杠为轴做圆周运动,运动到最高点时,与单杠间弹力大小为F,运动员在最高点的速度大小为v,其F-v2图象如图乙所示。取g=10 m/s2,则下列说法中正确的是( )。
A.此运动员的质量为55 kg
B.此运动员的重心到单杠的距离为0.9 m
C.运动员在最高点速度为4 m/s时,其受单杠的弹力方向向上
D.在完成“单臂大回环”的过程中,他的单臂至少要承受2750 N的力
√
7
√
√
1
2
3
4
5
6
【解析】对运动员在最高点进行受力分析,速度为零时,F-mg=0,结合图象解得质量m=55kg,所以A项正确;当F=0时,由向心力公式可得mg= ,结合图象可知R=0.9m,即运动员的重心到单杠的距离为0.9m,B项正确;在最高点速度为4m/s时,运动员受单杆的拉力,所以C项错误;经过最低点时,受力最大,由牛顿第二定律得F-mg=m ,根据机械能守恒得mg·2R= mv2,由以上两式得F=5mg,代入数据得F=2750N,即运动员的单臂至少要承受的力为2750N,所以D项正确。
7
【变式训练6】如图甲所示,两段长均为L轻质线共同系住一个质量为m的小球,另一端分别固定在等高的A、B两点,A、B两点间距也为L,今使小球在竖直平面内做圆周运动,当小球到达最高点时速率为v,两段线中张力恰好均为零;若小球到达最高点时速率为2v,则此时每段线中张力大小为( )。
mg B.2mg C.3mg D.4mg
【解析】当小球到达最高点时速率为v,两段线中张力恰好均为零,有mg=m ;当小球到达最高点时速率为2v,设每段线中张力大小为F,如图乙所示,应有2Fcos30°+mg=m ,解得F= mg,A项正确。
1
2
3
4
5
6
7
√
2021年高中模型问题专项突破
模型概述
01
竖直平面内两类典型模型分析
轻绳模型
轻杆模型
实例
如球与绳连接、沿内轨道运动的球等
如球与杆连接、球在内壁光滑的圆管内运动等
图示
最高点无支撑
最高点有支撑
最
高
点
受力特征
重力、弹力,弹力方向指向圆心
重力、弹力,弹力方向指向圆心或背离圆心
受力示意图
力学方程
mg+FN=m
mg±FN=m
临界特征
FN=0,vmin=
竖直向上的FN=mg,v=0
过最高点条件
v≥
v≥0
速度和弹力关系讨论
分析
①能过最高点时,v≥ ,FN+mg=m ,绳、轨道对球产生弹力FN
②不能过最高点时,v< ,在到达最高点前小球已经脱离了圆轨道做斜抛运动
①当v=0时,FN=mg,FN为支持力,沿半径背离圆心
②当0
④当v> 时,FN+mg=m ,FN指向圆心并随v的增大而增大
02
精讲精练
【典例1】“水流星”是一个经典的杂技表演项目,杂技演员将装水的杯子(可视为质点)用细绳系着让杯子在竖直平面内做圆周运动。杯子到最高点时杯口向下,水也不会从杯中流出,如图所示。若杯子质量为m,所装水的质量为M,杯子运动到圆周的最高点时,水对杯底刚好无压力,重力加速度为g,则杯子运动到圆周最高点时,杂技演员对细绳的拉力大小为( )。
A.0 B.mg C.Mg D.(M+m)g
【解析】杯子到最高点时,由于水刚好没有流出,则杯底对水的作用力为零,设这时杯子的速度大小为v,对水研究有Mg=M ,对杯子和水整体研究,设绳的拉力为F,则F+(M+m)g=(M+m) ,解得F=0,A项正确。
√
【变式训练1】如图3所示为模拟过山车的实验装置,小球从左侧的最高点释放后能够通过竖直圆轨道而到达右侧.若竖直圆轨道的半径为R,要使小球能顺利通过竖直圆轨道,则小球通过竖直圆轨道的最高点时的角速度最小为( )
A. B.2 C. D.
【解析】小球能通过竖直圆轨道的最高点的临界状态为重力提供向心力,即mg=mω2R,解得ω= ,选项C正确.
√
【变式训练2】 一细绳与水桶相连,水桶中装有水,水桶与细绳一起在竖直平面内做圆周运动,如图2所示,水的质量m=0.5 kg,水的重心到转轴的距离r=50 cm.(g取10 m/s2)
(1)若在最高点水不流出来,求桶最小速率;(结果保留三位有效数字)
(2)若在最高点水桶的速率v=3 m/s,求水对桶底的压力大小.
【答案】(1)2.24 m/s (2)4 N
【解析】(1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,此时桶的速率最小.
此时有:mg=m ,
则所求的最小速率为:
v0= ≈2.24 m/s.
(2)此时桶底对水有一向下的压力,设为FN,则由牛顿第二定律有:
FN+mg=m ,
代入数据可得:FN=4 N.
由牛顿第三定律,水对桶底的压力:
FN′=4 N.
【典例2】长度为0.5 m的轻杆OA绕O点在竖直平面内做圆周运动,A端连着一个质量m=2 kg的小球.求在下述的两种情况下,通过最高点时小球对杆的作用力的大小和方向.(g取10 m/s2)
(1)杆做匀速圆周运动的转速为2.0 r/s;
(2)杆做匀速圆周运动的转速为0.5 r/s.
【答案】(1)小球对杆的拉力为138 N,方向竖直向上
【解析】 小球在最高点的受力如图所示:
(1)杆的转速为2.0 r/s时,ω=2π·n=4π rad/s
由牛顿第二定律得F+mg=mLω2
故小球所受杆的作用力
F=mLω2-mg=2×(0.5×42×π2-10)N≈138 N
即杆对小球提供了138 N的拉力.
由牛顿第三定律知小球对杆的拉力大小为138 N,方向竖直向上.
(2)杆的转速为0.5 r/s时,ω′=2π·n=π rad/s
同理可得小球所受杆的作用力
F=mLω′2-mg=2×(0.5×π2-10)N≈-10 N.
力F为负值表示它的方向与受力分析中所假设的方向相反,故小球对杆的压力大小为10 N,方向竖直向下.
【变式训练3】 (多选)如图所示,一个固定在竖直平面上的光滑圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,下列说法中正确的是( )
A.小球通过管道最低点时,小球对管道的压力向下
B.小球通过管道最低点时,小球对管道的压力向上
C.小球通过管道最高点时,小球对管道的压力可能向上
D.小球通过管道最高点时,小球对管道可能无压力
√
【解析】设管道的半径为R,小球的质量为m,小球通过最低点时速度大小为v1,根据牛顿第二定律:N-mg=m 可知小球所受合力向上,则管道对小球的支持力向上,则小球对管道的压力向下,故A正确,B错误;最高点时速度大小为v2,根据牛顿第二定律:mg-N=m ,当v2= 时,N=0,说明管道对小球无压力;当v2> 时,N<0,说明管道对小球的作用力向下,则小球对管道的压力向上,故C、D正确.所以A、C、D正确,B错误.
【变式训练4】(多选)如图所示,半径为R的光滑细圆环轨道被固定在竖直平面上,轨道正上方和正下方分别有质量为2m和m的静止小球A、B,它们由长为2R的轻杆固定连接,圆环轨道内壁开有环形小槽,可使细杆无摩擦、无障碍地绕其中心点转动。今对上方小球A施加微小扰动。两球开始运动后,下列说法正确的是( )。
A.轻杆转到水平位置时,两球的线速度大小相等
B.轻杆转到竖直位置时,两球的加速度大小不相等
C.运动过程中,A球速度的最大值为
D.当A球运动到最低点时,两小球对轨道作用力的合力大小为 mg
√
√
√
【解析】两球做圆周运动,在任意位置角速度相等,则线速度和向心加速度大小相等,A项正确,B项错误;A、B两球组成的系统机械能守恒,当系统重力势能最小(A为最低点)时,线速度最大,则mg·2R= ×3mv2,最大速度v= ,C项正确;A在最低点时,分别对A、B受力分析,有FNA-2mg=2m ,FNB+mg=m ,则FNA-FNB= ,D项正确。
1
2
3
4
5
6
【变式训练5】(多选)如图甲所示,我国男子体操运动员在里约奥运会上个人全能中完成“单臂大回环”的高难度动作:用一只手抓住单杠,伸展身体,以单杠为轴做圆周运动,运动到最高点时,与单杠间弹力大小为F,运动员在最高点的速度大小为v,其F-v2图象如图乙所示。取g=10 m/s2,则下列说法中正确的是( )。
A.此运动员的质量为55 kg
B.此运动员的重心到单杠的距离为0.9 m
C.运动员在最高点速度为4 m/s时,其受单杠的弹力方向向上
D.在完成“单臂大回环”的过程中,他的单臂至少要承受2750 N的力
√
7
√
√
1
2
3
4
5
6
【解析】对运动员在最高点进行受力分析,速度为零时,F-mg=0,结合图象解得质量m=55kg,所以A项正确;当F=0时,由向心力公式可得mg= ,结合图象可知R=0.9m,即运动员的重心到单杠的距离为0.9m,B项正确;在最高点速度为4m/s时,运动员受单杆的拉力,所以C项错误;经过最低点时,受力最大,由牛顿第二定律得F-mg=m ,根据机械能守恒得mg·2R= mv2,由以上两式得F=5mg,代入数据得F=2750N,即运动员的单臂至少要承受的力为2750N,所以D项正确。
7
【变式训练6】如图甲所示,两段长均为L轻质线共同系住一个质量为m的小球,另一端分别固定在等高的A、B两点,A、B两点间距也为L,今使小球在竖直平面内做圆周运动,当小球到达最高点时速率为v,两段线中张力恰好均为零;若小球到达最高点时速率为2v,则此时每段线中张力大小为( )。
mg B.2mg C.3mg D.4mg
【解析】当小球到达最高点时速率为v,两段线中张力恰好均为零,有mg=m ;当小球到达最高点时速率为2v,设每段线中张力大小为F,如图乙所示,应有2Fcos30°+mg=m ,解得F= mg,A项正确。
1
2
3
4
5
6
7
√
同课章节目录
