【备考2021】高中物理模型问题专项突破 13变力做功 课件(20张ppt)
文档属性
| 名称 | 【备考2021】高中物理模型问题专项突破 13变力做功 课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 410.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-12 13:55:38 | ||
图片预览








文档简介
模型13 变力做功
2021年高中模型问题专项突破
模型概述
01
1.化变力为恒力
变力做功直接求解时,往往都比较复杂,若通过转换研究对象,有时可以化为恒力,用W=Flcos α求解。此方法常应用于轻绳通过定滑轮拉物体的问题中。
2.利用平均力求变力做功
在求解变力做功时,若物体受到的力的方向不变,而大小随位移呈线性变化,即力均匀变化时,则可以等效为物体受到一大小为 = 的恒力做功,F1、F2分别为物体初、末状态所受到的力,然后用公式W= lcos α求此力所做的功。
3.利用F-x图象求变力做功
在F-x图象中,图线与x轴所围“面积”的代数和就表示力F在这段位移所做的功,且位于x轴上方的“面积”为正,位于x轴下方的“面积”为负。
4.利用动能定理求变力做功
动能定理既适用于直线运动,也适用于曲线运动;既适用于求恒力做功,也适用于求变力做功。使用动能定理可根据动能的变化来求功,是求变力做功的一种方法。
5.利用W=Pt求变力做功
这是一种等效代换的观点,用W=Pt计算功时,必须满足变力的功率是一定的这一条件。
02
精讲精练
【典例1】如图所示,固定的光滑竖直杆上套着一个滑块,滑块用轻绳系着绕过光滑的定滑轮O。现以大小不变的拉力F拉绳,使滑块从A点起由静止开始上升。滑块运动到C点时速度最大。已知滑块的质量为m,滑轮O到竖直杆的距离为d,∠OAO'=37°,∠OCO'=53°,重力加速度为g,sin 37°=0.6
cos 37°=0.8。求:
(1)拉力F的大小。
(2)滑块由A到C过程中拉力F做的功。
【答案】(1) mg (2) mgd
【解析】(1)对滑块进行受力分析,其到C点时速度最大,则其所受合力为零,根据共点力的平衡条件,有
Fcos 53°=mg 解得F= mg。
(2)由能量的转化与守恒可知,拉力F对绳端点做的功就等于绳的拉力F对滑块做的功
滑轮与A点间绳长L1=
滑轮与C点间绳长L2=
滑轮右侧绳子增大的长度
ΔL=L1-L2=
拉力做功W=FΔL= mgd。
【变式训练1】如图所示,固定的光滑竖直杆上套着一个滑块,用轻绳系着滑块绕过光滑的定滑轮,以大小恒定的拉力F拉绳,使滑块从A点起由静止开始上升。若从A点上升至B点和从B点上升至C点的过程中拉力F做的功分别为W1和W2,图中AB=BC,则( )。
A.W1>W2 B.W1【解析】拉力F为恒力,W=F·Δl,Δl为绳拉滑块过程中力F的作用点移动的位移,大小等于滑轮左侧绳长的缩短量,由图可知,ΔlAB>ΔlBC,故W1>W2,A项正确。
√
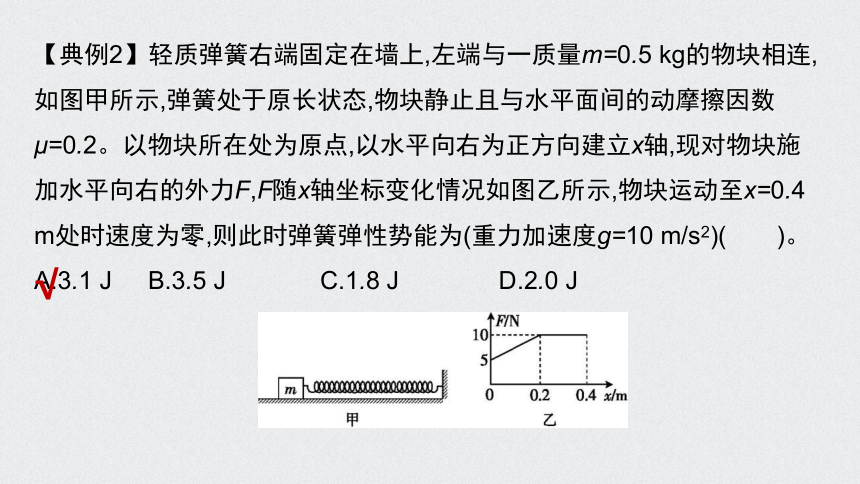
【典例2】轻质弹簧右端固定在墙上,左端与一质量m=0.5 kg的物块相连,如图甲所示,弹簧处于原长状态,物块静止且与水平面间的动摩擦因数μ=0.2。以物块所在处为原点,以水平向右为正方向建立x轴,现对物块施加水平向右的外力F,F随x轴坐标变化情况如图乙所示,物块运动至x=0.4 m处时速度为零,则此时弹簧弹性势能为(重力加速度g=10 m/s2)( )。
A.3.1 J B.3.5 J C.1.8 J D.2.0 J
√
【解析】物块与水平面间的摩擦力Ff=μmg=1 N。现对物块施加水平向右的外力F,由F-x图线与x轴所围“面积”表示功可知F做功W=3.5 J,克服摩擦力做功Wf=Ffx=0.4 J。由于物块运动至x=0.4 m处时,速度为0,由功能关系可知,W-Wf=Ep,此时弹簧的弹性势能Ep=3.1 J,A项正确。
【变式训练2】某星球半径R=6×106 m,假设该星球表面上有一倾角θ=30°的固定斜面体,一质量m=1 kg的小物块在力F作用下从静止开始沿斜面向上运动,力F始终与斜面平行,如图所示。已知小物块和斜面间的动摩擦因数μ= ,力F随位移x变化的规律如图所示(取沿斜面向上为正方向),如果小物块运动12 m时速度恰好为零,已知引力常量G=6.67×10-11 N·m2/kg2。求:(计算结果保留1位有效数字)
(1)该星球表面上的重力加速度g的大小。
(2)该星球的平均密度。
【答案】(1)6 m/s2 (2)4×103 kg/m3
【解析】(1)物块上滑过程中力F所做的功WF=(15×6-3×6) J=72 J
由动能定理得WF-mgsin θ·x-μmgcos θ·x=0
解得g=6 m/s2。
(2)在星球表面重力与万有引力大小相等,有mg=G
可得星球的质量M=
所以星球的密度
ρ= = = ≈4×103 kg/m3。
【典例3】(多选)如图所示,摆球质量为m,悬线长为L,把悬线拉到水平位置后放手。设在摆球运动过程中空气阻力F阻的大小不变,则下列说法正确的是( )。
A.重力做功为mgL B.悬线的拉力做功为0
C.空气阻力F阻做功为-mgL D.空气阻力F阻做功为- F阻πL/2
【答案】ABD
【解析】由重力做功特点可知重力做功WG=mgL,A项正确;悬线的拉力始终与摆球的运动方向垂直,不做功,B项正确;由微元法可得空气阻力做功WF阻=- F阻πL/2,D项正确。
√
√
√
【变式训练3】如图甲所示,水平平台上有一个质量m=50 kg的物块,站在水平地面上的人用跨过定滑轮的细绳向右拉动物块,细绳不可伸长。不计滑轮的大小、质量和绳与滑轮间的摩擦。在人以速度v=0.5 m/s从平台边缘正下方匀速向右前进x=4 m的过程中,始终保持桌面和手的竖直高度差h=3 m不变。已知物块与平台间的动摩擦因数μ=0.5,重力加速度g=10 m/s2。求人克服细绳的拉力做的功。
【答案】504 J
【解析】设人发生x的位移时,绳与水平方向的夹角为θ,由运动的分解可得,物块的速度v1=vcos θ
由几何关系得cos θ=
在此过程中,物块的位移
s= -h=2 m
物块克服摩擦力做的功Wf=μmgs
对物块,由动能定理得WT-Wf= m
所以人克服细绳的拉力做的功
WT= +μmgs=504 J。
1
2
3
4
5
6
【典例4】质量为1.0×103 kg的汽车,沿倾角为30°的斜坡由静止开始运动,汽车在运动过程中所受摩擦阻力大小恒为2000 N,汽车发动机的额定输出功率为5.6×104 W,开始时汽车以a=1 m/s2的加速度做匀加速运动。(重力加速度g=10 m/s2)
(1)求汽车做匀加速运动的时间t1。
(2)求汽车所能达到的最大速率。
(3)若斜坡长143.5 m,且认为汽车到达坡顶时恰好达到最大速率,则汽车从坡底到坡顶需多长时间?
【答案】(1)7 s (2)8 m/s (3)22 s
7
1
2
3
4
5
6
【解析】(1)由牛顿第二定律得 F-mgsin 30°-Ff=ma
设匀加速过程的末速度为v,则有P=Fv
v=at1 解得t1=7 s。
(2)当达到最大速度vm时,a=0,则有
P=(mgsin 30°+Ff)vm 解得vm=8 m/s。
(3)汽车做匀加速运动的位移x1= a
在后一阶段对汽车由动能定理得
Pt2-(mgsin 30°+Ff)x2= m - mv2
又x=x1+x2 解得t2≈15 s
故汽车运动的总时间t=t1+t2=22 s。
7
【典例5】如图所示,顶角 的金属导轨 固定在水平面内,导轨处在方向竖直,磁感应强度为 的匀强磁场中,一根与 垂直的导体棒在水平外力作用下的恒定速度 沿导轨 向右滑动,导体棒的质量为m ,导轨与导体棒单位长度的电阻均为r ,导体棒与导轨接触点为 a和b ,导体棒在滑动过程中始终保持与导轨良好接触,t=0时,导体棒位于顶角处。
求 (1) 时刻流过导体棒的电流强度 和电流方向。
(2)导体棒在 时间内产生的焦耳热 。
1
2
3
4
5
6
7
【解析】
⑴经时间 ,导体棒位移 ①
导体棒有效长度 ②
导体棒电动势 ③
回路总电阻 ④
⑤
①②③④⑤联立解得 ⑥
电流方向
(2)在t 时刻 ,
联立解得
为正比例函数关系,作出其图像, 当 线在 时间内时间所围面积。
2021年高中模型问题专项突破
模型概述
01
1.化变力为恒力
变力做功直接求解时,往往都比较复杂,若通过转换研究对象,有时可以化为恒力,用W=Flcos α求解。此方法常应用于轻绳通过定滑轮拉物体的问题中。
2.利用平均力求变力做功
在求解变力做功时,若物体受到的力的方向不变,而大小随位移呈线性变化,即力均匀变化时,则可以等效为物体受到一大小为 = 的恒力做功,F1、F2分别为物体初、末状态所受到的力,然后用公式W= lcos α求此力所做的功。
3.利用F-x图象求变力做功
在F-x图象中,图线与x轴所围“面积”的代数和就表示力F在这段位移所做的功,且位于x轴上方的“面积”为正,位于x轴下方的“面积”为负。
4.利用动能定理求变力做功
动能定理既适用于直线运动,也适用于曲线运动;既适用于求恒力做功,也适用于求变力做功。使用动能定理可根据动能的变化来求功,是求变力做功的一种方法。
5.利用W=Pt求变力做功
这是一种等效代换的观点,用W=Pt计算功时,必须满足变力的功率是一定的这一条件。
02
精讲精练
【典例1】如图所示,固定的光滑竖直杆上套着一个滑块,滑块用轻绳系着绕过光滑的定滑轮O。现以大小不变的拉力F拉绳,使滑块从A点起由静止开始上升。滑块运动到C点时速度最大。已知滑块的质量为m,滑轮O到竖直杆的距离为d,∠OAO'=37°,∠OCO'=53°,重力加速度为g,sin 37°=0.6
cos 37°=0.8。求:
(1)拉力F的大小。
(2)滑块由A到C过程中拉力F做的功。
【答案】(1) mg (2) mgd
【解析】(1)对滑块进行受力分析,其到C点时速度最大,则其所受合力为零,根据共点力的平衡条件,有
Fcos 53°=mg 解得F= mg。
(2)由能量的转化与守恒可知,拉力F对绳端点做的功就等于绳的拉力F对滑块做的功
滑轮与A点间绳长L1=
滑轮与C点间绳长L2=
滑轮右侧绳子增大的长度
ΔL=L1-L2=
拉力做功W=FΔL= mgd。
【变式训练1】如图所示,固定的光滑竖直杆上套着一个滑块,用轻绳系着滑块绕过光滑的定滑轮,以大小恒定的拉力F拉绳,使滑块从A点起由静止开始上升。若从A点上升至B点和从B点上升至C点的过程中拉力F做的功分别为W1和W2,图中AB=BC,则( )。
A.W1>W2 B.W1
√
【典例2】轻质弹簧右端固定在墙上,左端与一质量m=0.5 kg的物块相连,如图甲所示,弹簧处于原长状态,物块静止且与水平面间的动摩擦因数μ=0.2。以物块所在处为原点,以水平向右为正方向建立x轴,现对物块施加水平向右的外力F,F随x轴坐标变化情况如图乙所示,物块运动至x=0.4 m处时速度为零,则此时弹簧弹性势能为(重力加速度g=10 m/s2)( )。
A.3.1 J B.3.5 J C.1.8 J D.2.0 J
√
【解析】物块与水平面间的摩擦力Ff=μmg=1 N。现对物块施加水平向右的外力F,由F-x图线与x轴所围“面积”表示功可知F做功W=3.5 J,克服摩擦力做功Wf=Ffx=0.4 J。由于物块运动至x=0.4 m处时,速度为0,由功能关系可知,W-Wf=Ep,此时弹簧的弹性势能Ep=3.1 J,A项正确。
【变式训练2】某星球半径R=6×106 m,假设该星球表面上有一倾角θ=30°的固定斜面体,一质量m=1 kg的小物块在力F作用下从静止开始沿斜面向上运动,力F始终与斜面平行,如图所示。已知小物块和斜面间的动摩擦因数μ= ,力F随位移x变化的规律如图所示(取沿斜面向上为正方向),如果小物块运动12 m时速度恰好为零,已知引力常量G=6.67×10-11 N·m2/kg2。求:(计算结果保留1位有效数字)
(1)该星球表面上的重力加速度g的大小。
(2)该星球的平均密度。
【答案】(1)6 m/s2 (2)4×103 kg/m3
【解析】(1)物块上滑过程中力F所做的功WF=(15×6-3×6) J=72 J
由动能定理得WF-mgsin θ·x-μmgcos θ·x=0
解得g=6 m/s2。
(2)在星球表面重力与万有引力大小相等,有mg=G
可得星球的质量M=
所以星球的密度
ρ= = = ≈4×103 kg/m3。
【典例3】(多选)如图所示,摆球质量为m,悬线长为L,把悬线拉到水平位置后放手。设在摆球运动过程中空气阻力F阻的大小不变,则下列说法正确的是( )。
A.重力做功为mgL B.悬线的拉力做功为0
C.空气阻力F阻做功为-mgL D.空气阻力F阻做功为- F阻πL/2
【答案】ABD
【解析】由重力做功特点可知重力做功WG=mgL,A项正确;悬线的拉力始终与摆球的运动方向垂直,不做功,B项正确;由微元法可得空气阻力做功WF阻=- F阻πL/2,D项正确。
√
√
√
【变式训练3】如图甲所示,水平平台上有一个质量m=50 kg的物块,站在水平地面上的人用跨过定滑轮的细绳向右拉动物块,细绳不可伸长。不计滑轮的大小、质量和绳与滑轮间的摩擦。在人以速度v=0.5 m/s从平台边缘正下方匀速向右前进x=4 m的过程中,始终保持桌面和手的竖直高度差h=3 m不变。已知物块与平台间的动摩擦因数μ=0.5,重力加速度g=10 m/s2。求人克服细绳的拉力做的功。
【答案】504 J
【解析】设人发生x的位移时,绳与水平方向的夹角为θ,由运动的分解可得,物块的速度v1=vcos θ
由几何关系得cos θ=
在此过程中,物块的位移
s= -h=2 m
物块克服摩擦力做的功Wf=μmgs
对物块,由动能定理得WT-Wf= m
所以人克服细绳的拉力做的功
WT= +μmgs=504 J。
1
2
3
4
5
6
【典例4】质量为1.0×103 kg的汽车,沿倾角为30°的斜坡由静止开始运动,汽车在运动过程中所受摩擦阻力大小恒为2000 N,汽车发动机的额定输出功率为5.6×104 W,开始时汽车以a=1 m/s2的加速度做匀加速运动。(重力加速度g=10 m/s2)
(1)求汽车做匀加速运动的时间t1。
(2)求汽车所能达到的最大速率。
(3)若斜坡长143.5 m,且认为汽车到达坡顶时恰好达到最大速率,则汽车从坡底到坡顶需多长时间?
【答案】(1)7 s (2)8 m/s (3)22 s
7
1
2
3
4
5
6
【解析】(1)由牛顿第二定律得 F-mgsin 30°-Ff=ma
设匀加速过程的末速度为v,则有P=Fv
v=at1 解得t1=7 s。
(2)当达到最大速度vm时,a=0,则有
P=(mgsin 30°+Ff)vm 解得vm=8 m/s。
(3)汽车做匀加速运动的位移x1= a
在后一阶段对汽车由动能定理得
Pt2-(mgsin 30°+Ff)x2= m - mv2
又x=x1+x2 解得t2≈15 s
故汽车运动的总时间t=t1+t2=22 s。
7
【典例5】如图所示,顶角 的金属导轨 固定在水平面内,导轨处在方向竖直,磁感应强度为 的匀强磁场中,一根与 垂直的导体棒在水平外力作用下的恒定速度 沿导轨 向右滑动,导体棒的质量为m ,导轨与导体棒单位长度的电阻均为r ,导体棒与导轨接触点为 a和b ,导体棒在滑动过程中始终保持与导轨良好接触,t=0时,导体棒位于顶角处。
求 (1) 时刻流过导体棒的电流强度 和电流方向。
(2)导体棒在 时间内产生的焦耳热 。
1
2
3
4
5
6
7
【解析】
⑴经时间 ,导体棒位移 ①
导体棒有效长度 ②
导体棒电动势 ③
回路总电阻 ④
⑤
①②③④⑤联立解得 ⑥
电流方向
(2)在t 时刻 ,
联立解得
为正比例函数关系,作出其图像, 当 线在 时间内时间所围面积。
同课章节目录
