【备考2021】高中物理模型问题专项突破 18带电粒子在有界磁场中的运动 课件(20张ppt)
文档属性
| 名称 | 【备考2021】高中物理模型问题专项突破 18带电粒子在有界磁场中的运动 课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 536.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-12 14:05:09 | ||
图片预览






文档简介
模型18 带电粒子在有界磁场中的运动
2021年高中模型问题专项突破
模型概述
01
1.带电粒子在有界匀强磁场中做圆周运动的分析
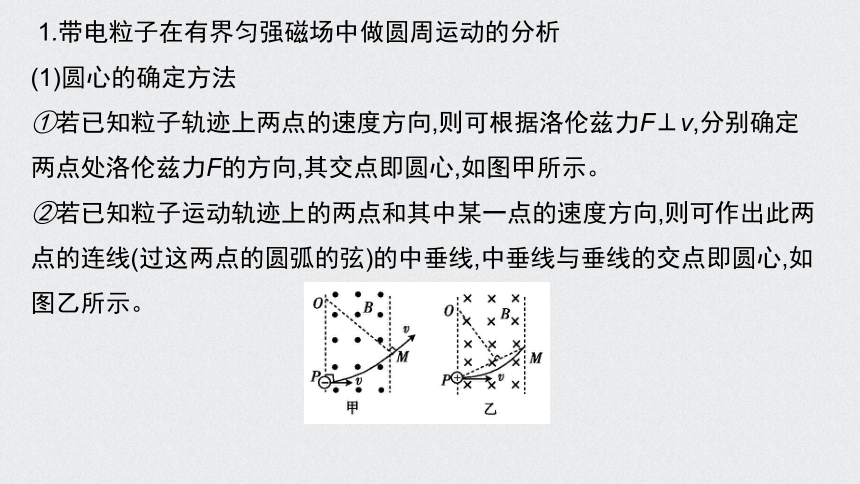
(1)圆心的确定方法
①若已知粒子轨迹上两点的速度方向,则可根据洛伦兹力F⊥v,分别确定两点处洛伦兹力F的方向,其交点即圆心,如图甲所示。
②若已知粒子运动轨迹上的两点和其中某一点的速度方向,则可作出此两点的连线(过这两点的圆弧的弦)的中垂线,中垂线与垂线的交点即圆心,如图乙所示。
(2)半径的计算方法
①由公式求:半径R= 。
②由几何方法求:一般由数学知识(勾股定理、三角函数等)计算来确定。
(3)时间的计算方法
①由圆心角求:t= ·T。
②由弧长求:t= 。
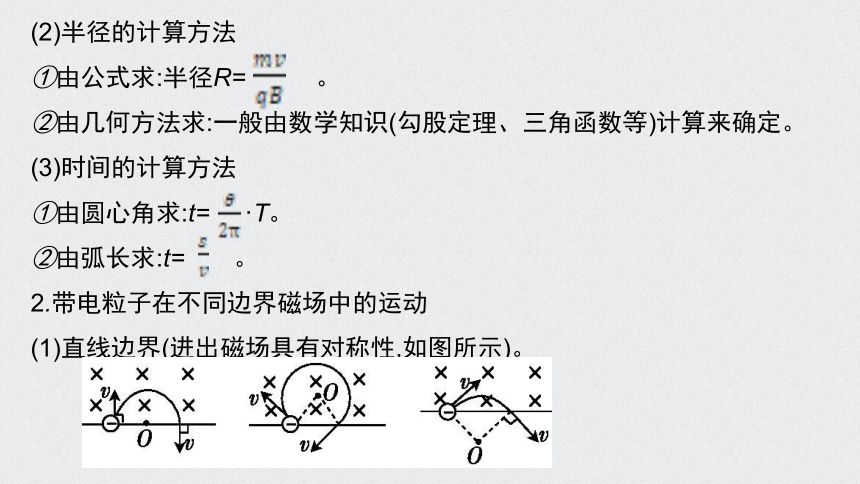
2.带电粒子在不同边界磁场中的运动
(1)直线边界(进出磁场具有对称性,如图所示)。
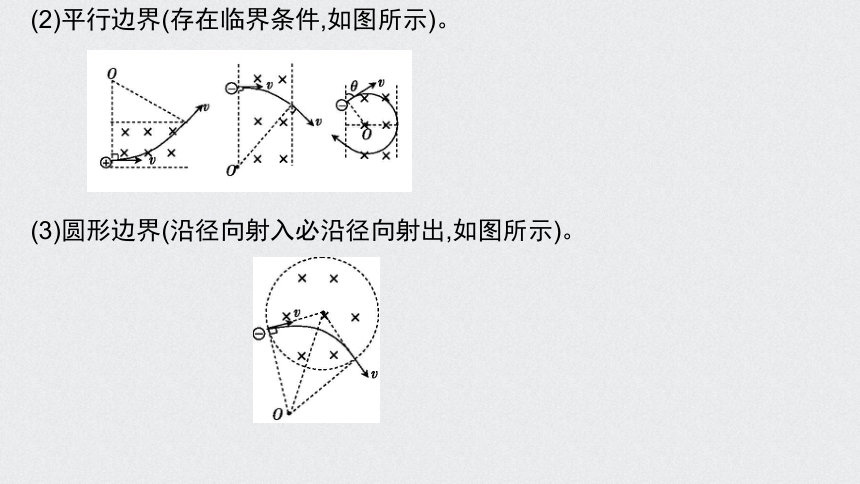
(2)平行边界(存在临界条件,如图所示)。
(3)圆形边界(沿径向射入必沿径向射出,如图所示)。
02
精讲精练
【典例1】(2019广东惠州一月模拟)如图甲所示,直线MN上方有垂直纸面向里的匀强磁场,电子1从磁场边界上的a点垂直MN和磁场方向射入磁场,经t1时间从b点离开磁场。之后电子2也由a点沿图示方向以相同速率垂直磁场方向射入磁场,经t2时间从a、b连线的中点c离开磁场,则t1∶t2为( )。
A.2∶3 B.3∶1 C.3∶2 D.2∶1
√
【解析】粒子在磁场中都做匀速圆周运动,根据题意画出粒子的运动轨迹,如图乙所示。电子1垂直射进磁场,从b点离开,则运动了半个圆周,ab为直径,c点为圆心,电子2以相同速率垂直磁场方向射入磁场,经t2时间从a、b连线的中点c离开磁场,根据半径r= 可知,粒子1和2的运行轨迹半径相等,根据几何关系可知,△aOc为等边三角形,则粒子2转过的圆心角为60°,所以粒子1运动的时间t1= = ,粒子2运动的时间t2= = 、
故 = ,B项正确。
【变式训练1】如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁感应强度为B。在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计)。则下列说法正确的是( )。
A.若v一定,θ越大,则粒子在磁场中运动的时间越短
B.若v一定,θ越大,则粒子离开磁场的位置距O点越远
C.若θ一定,v越大,则粒子在磁场中运动的角速度越大
D.若θ一定,v越大,则粒子在磁场中运动的时间越短
√
【解析】由左手定则可知,带正电的粒子向左偏转。若v一定,θ越大,则粒子在磁场中运动的时间越短,A项正确;若v一定,θ等于90°时,粒子离开磁场的位置距O点最远,B项错误;若θ一定,粒子在磁场中运动的周期与v无关,由ω= 可知粒子在磁场中运动的角速度与v无关,C、D两项错误。
【典例2】(2018山东济南第二次模拟)如图甲所示,有界匀强磁场边界线SP∥MN,速率不同的同种带电粒子从S点沿SP方向同时射入磁场,粒子的带电荷量相同,其中从a点射出的粒子速度v1的方向与MN垂直;从b点射出的粒子速度v2的方向与MN成60°角,设两粒子从S到a、b所需时间分别为t1和t2,则t1∶t2为(重力不计)( )。
A.1∶3 B.4∶3
C.1∶1 D.3∶2
√
【解析】粒子在磁场中的运动轨迹如图乙所示,可求出从a点射出的粒子对应的圆心角为90°,从b点射出的粒子对应的圆心角为60°,由t= · 可得t1∶t2=90°∶60°=3∶2,D项正确。
【变式训练2】(2018贵州贵阳三校联考)(多选)如图甲所示,在正方形abcd内充满方向垂直纸面向里、磁感应强度为B的匀强磁场。a处有比荷相等的P、Q两种粒子,P粒子以速度v1沿ab方向垂直射入磁场,经时间t1从d点射出磁场,Q粒子沿与ab成30°角的方向以速度v2垂直射入磁场,经时间t2垂直cd射出磁场,不计粒子重力和粒子间的相互作用力,则下列说法中正确的是( )。
A.v1∶v2=1∶2 B.v1∶v2= ∶4
C.t1∶t2=2∶1 D.t1∶t2=3∶1
√
√
【解析】P、Q两粒子的运动轨迹如图乙所示,粒子在磁场中的运行周期T= ,因为两种粒子的比荷相等,故T1=T2。设正方形的边长为L,则由图知P粒子运行半径r1= ,运行时间t1= ,乙粒子运行半径r2= ,运行时间t2= ,而r= ,所以v1∶v2=r1∶r2= ∶4,A项错误,B项正确;t1∶t2=3∶1,C项错误,D项正确。
【典例3】 (2019福建泉州质量检测)(多选)如图甲所示,两方向相反、磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC理想分开,三角形内磁场垂直纸面向里,三角形顶点A处有一质子源,能沿∠BAC的角平分线发射速度不同的质子(质子重力不计),所有质子均能通过C点,质子比荷 =k,则质子的速度可能为( )。
A.2BkL B. C. D.
【解析】因质子带正电,且经过C点,其可能的轨迹如图乙所示,所有圆弧所对圆心角均为60°,所以质子运行的半径r= (n=1,2,3,…),由洛伦兹力提供向心力得Bqv=m ,即v= =Bk· (n=1,2,3,…),B、D两项正确。
√
√
【变式训练3】(多选)如图甲所示,在直角三角形ABC内充满垂直纸面向外匀强磁场(图中未画出),AB边长度为d,∠B= 。现垂直AB边射入一群质量均为m、电荷量均为q、速度大小均为v的带正电粒子,已知垂直AC边射出粒子在磁场中运动的时间为t,而运动时间最长的粒子在磁场中的运动时间为 t(不计重力)。则下列判断中正确是( )。
A.粒子在磁场中做匀速圆周运动的周期为4t
B.该匀强磁场的磁感应强度大小为
C.粒子在磁场中运动的轨道半径为 d
D.粒子进入磁场时的速度大小为
√
√
√
【解析】带电粒子在磁场中做匀速圆周运动,垂直AC边射出的粒子在磁场中运动的时间是 T,即 T=t,则得周期T=4t,A项正确;由T=4t,R= ,
T= ,得B0= = ,B项正确;运动时间最长的粒子在磁场中运动的轨迹如图乙所示,根据几何关系有Rsin + =d,解得R= d,C项正确;根据粒子在磁场中运动的速度v= ,周期T=4t0,半径R= d,联立可得v= , D项错误。
1
2
3
4
5
6
【典例4】空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直横截面。一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°。不计重力,该磁场的磁感应强度大小为
A. B. C. D.
【解析】 根据题意,画出粒子的运动轨迹,由图中几何关系可知,粒子做圆周运动的半径 ,由
可知, ,综上所述,正确答案为A。
√
7
1
2
3
4
5
6
【变式训练4】如图甲所示,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外。一带电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为 ,已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( )。
A. B. C. D.
7
√
【解析】如图乙所示,粒子做圆周运动的圆心O2必在过入射点垂直于入射速度方向的直线EF上,由于粒子射入、射出磁场时运动方向间的夹角为60°,故圆弧ENM对应的圆心角为60°,所以△EMO2为等边三角形。由于O1D= ,所以∠EO1D=60°,△O1ME为等边三角形,所以可得到粒子做圆周运动的半径EO2=O1E=R,由qvB= ,得v= ,B项正确。
1
2
3
4
5
6
7
2021年高中模型问题专项突破
模型概述
01
1.带电粒子在有界匀强磁场中做圆周运动的分析
(1)圆心的确定方法
①若已知粒子轨迹上两点的速度方向,则可根据洛伦兹力F⊥v,分别确定两点处洛伦兹力F的方向,其交点即圆心,如图甲所示。
②若已知粒子运动轨迹上的两点和其中某一点的速度方向,则可作出此两点的连线(过这两点的圆弧的弦)的中垂线,中垂线与垂线的交点即圆心,如图乙所示。
(2)半径的计算方法
①由公式求:半径R= 。
②由几何方法求:一般由数学知识(勾股定理、三角函数等)计算来确定。
(3)时间的计算方法
①由圆心角求:t= ·T。
②由弧长求:t= 。
2.带电粒子在不同边界磁场中的运动
(1)直线边界(进出磁场具有对称性,如图所示)。
(2)平行边界(存在临界条件,如图所示)。
(3)圆形边界(沿径向射入必沿径向射出,如图所示)。
02
精讲精练
【典例1】(2019广东惠州一月模拟)如图甲所示,直线MN上方有垂直纸面向里的匀强磁场,电子1从磁场边界上的a点垂直MN和磁场方向射入磁场,经t1时间从b点离开磁场。之后电子2也由a点沿图示方向以相同速率垂直磁场方向射入磁场,经t2时间从a、b连线的中点c离开磁场,则t1∶t2为( )。
A.2∶3 B.3∶1 C.3∶2 D.2∶1
√
【解析】粒子在磁场中都做匀速圆周运动,根据题意画出粒子的运动轨迹,如图乙所示。电子1垂直射进磁场,从b点离开,则运动了半个圆周,ab为直径,c点为圆心,电子2以相同速率垂直磁场方向射入磁场,经t2时间从a、b连线的中点c离开磁场,根据半径r= 可知,粒子1和2的运行轨迹半径相等,根据几何关系可知,△aOc为等边三角形,则粒子2转过的圆心角为60°,所以粒子1运动的时间t1= = ,粒子2运动的时间t2= = 、
故 = ,B项正确。
【变式训练1】如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁感应强度为B。在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计)。则下列说法正确的是( )。
A.若v一定,θ越大,则粒子在磁场中运动的时间越短
B.若v一定,θ越大,则粒子离开磁场的位置距O点越远
C.若θ一定,v越大,则粒子在磁场中运动的角速度越大
D.若θ一定,v越大,则粒子在磁场中运动的时间越短
√
【解析】由左手定则可知,带正电的粒子向左偏转。若v一定,θ越大,则粒子在磁场中运动的时间越短,A项正确;若v一定,θ等于90°时,粒子离开磁场的位置距O点最远,B项错误;若θ一定,粒子在磁场中运动的周期与v无关,由ω= 可知粒子在磁场中运动的角速度与v无关,C、D两项错误。
【典例2】(2018山东济南第二次模拟)如图甲所示,有界匀强磁场边界线SP∥MN,速率不同的同种带电粒子从S点沿SP方向同时射入磁场,粒子的带电荷量相同,其中从a点射出的粒子速度v1的方向与MN垂直;从b点射出的粒子速度v2的方向与MN成60°角,设两粒子从S到a、b所需时间分别为t1和t2,则t1∶t2为(重力不计)( )。
A.1∶3 B.4∶3
C.1∶1 D.3∶2
√
【解析】粒子在磁场中的运动轨迹如图乙所示,可求出从a点射出的粒子对应的圆心角为90°,从b点射出的粒子对应的圆心角为60°,由t= · 可得t1∶t2=90°∶60°=3∶2,D项正确。
【变式训练2】(2018贵州贵阳三校联考)(多选)如图甲所示,在正方形abcd内充满方向垂直纸面向里、磁感应强度为B的匀强磁场。a处有比荷相等的P、Q两种粒子,P粒子以速度v1沿ab方向垂直射入磁场,经时间t1从d点射出磁场,Q粒子沿与ab成30°角的方向以速度v2垂直射入磁场,经时间t2垂直cd射出磁场,不计粒子重力和粒子间的相互作用力,则下列说法中正确的是( )。
A.v1∶v2=1∶2 B.v1∶v2= ∶4
C.t1∶t2=2∶1 D.t1∶t2=3∶1
√
√
【解析】P、Q两粒子的运动轨迹如图乙所示,粒子在磁场中的运行周期T= ,因为两种粒子的比荷相等,故T1=T2。设正方形的边长为L,则由图知P粒子运行半径r1= ,运行时间t1= ,乙粒子运行半径r2= ,运行时间t2= ,而r= ,所以v1∶v2=r1∶r2= ∶4,A项错误,B项正确;t1∶t2=3∶1,C项错误,D项正确。
【典例3】 (2019福建泉州质量检测)(多选)如图甲所示,两方向相反、磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC理想分开,三角形内磁场垂直纸面向里,三角形顶点A处有一质子源,能沿∠BAC的角平分线发射速度不同的质子(质子重力不计),所有质子均能通过C点,质子比荷 =k,则质子的速度可能为( )。
A.2BkL B. C. D.
【解析】因质子带正电,且经过C点,其可能的轨迹如图乙所示,所有圆弧所对圆心角均为60°,所以质子运行的半径r= (n=1,2,3,…),由洛伦兹力提供向心力得Bqv=m ,即v= =Bk· (n=1,2,3,…),B、D两项正确。
√
√
【变式训练3】(多选)如图甲所示,在直角三角形ABC内充满垂直纸面向外匀强磁场(图中未画出),AB边长度为d,∠B= 。现垂直AB边射入一群质量均为m、电荷量均为q、速度大小均为v的带正电粒子,已知垂直AC边射出粒子在磁场中运动的时间为t,而运动时间最长的粒子在磁场中的运动时间为 t(不计重力)。则下列判断中正确是( )。
A.粒子在磁场中做匀速圆周运动的周期为4t
B.该匀强磁场的磁感应强度大小为
C.粒子在磁场中运动的轨道半径为 d
D.粒子进入磁场时的速度大小为
√
√
√
【解析】带电粒子在磁场中做匀速圆周运动,垂直AC边射出的粒子在磁场中运动的时间是 T,即 T=t,则得周期T=4t,A项正确;由T=4t,R= ,
T= ,得B0= = ,B项正确;运动时间最长的粒子在磁场中运动的轨迹如图乙所示,根据几何关系有Rsin + =d,解得R= d,C项正确;根据粒子在磁场中运动的速度v= ,周期T=4t0,半径R= d,联立可得v= , D项错误。
1
2
3
4
5
6
【典例4】空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直横截面。一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°。不计重力,该磁场的磁感应强度大小为
A. B. C. D.
【解析】 根据题意,画出粒子的运动轨迹,由图中几何关系可知,粒子做圆周运动的半径 ,由
可知, ,综上所述,正确答案为A。
√
7
1
2
3
4
5
6
【变式训练4】如图甲所示,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外。一带电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为 ,已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( )。
A. B. C. D.
7
√
【解析】如图乙所示,粒子做圆周运动的圆心O2必在过入射点垂直于入射速度方向的直线EF上,由于粒子射入、射出磁场时运动方向间的夹角为60°,故圆弧ENM对应的圆心角为60°,所以△EMO2为等边三角形。由于O1D= ,所以∠EO1D=60°,△O1ME为等边三角形,所以可得到粒子做圆周运动的半径EO2=O1E=R,由qvB= ,得v= ,B项正确。
1
2
3
4
5
6
7
同课章节目录
