人教版八年级数学下册 第十八章 平行四边形 测试卷(word版含答案)
文档属性
| 名称 | 人教版八年级数学下册 第十八章 平行四边形 测试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览


文档简介
八年级数学第十八章
平行四边形单元测试
(
时间:100分钟
总分:100分)
题号
一
二
三
四
五
总分
得分
一、选择题:(每题3分,共18分,请将答案填写在表格中)
题号
1
2
3
4
5
6
选项
1.下列说法中错误的是( )
A.
平行四边形的对角线互相平分
B.
两组对边分别相等的四边形是平行四边形
C.
有一组邻边相等且有一个角是直角的四边形是正方形
D.
矩形的对角线相等
2.顺次连接一个矩形各边的中点,得到的四边形一定是(
)
A.菱形
B.矩形
C.正方形
D.梯形
3.已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,则此菱形的面积为(
)
A.48cm2
B.24cm2
C.18cm2
D.12cm2
4.如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
A.
∠ABC=90°
B.
AC=BD
C.
OA=OB
D.
OA=AD
5.如图,正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为(
)
A.
8
B.
C.
10
D.
6.如图,正方形ABCD中,E、F均为中点,则下列结论中:
7.①AF⊥DE;
②AD=BP;
③PE+PF=PC;
④PE+PF=PC。其中正确的是( )
A.①④
B.①②④
C.①③
D.①②③
二、填空题(每小题3分,共18分)
7.已知在Rt△ABC中,斜边上的中线=5cm,则斜边AB的长=___________.
8.如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,∠AOB=50°,
则∠BAE的度数是
.
(第八题图)
(第九题图)
9.如图,在平行四边形中,是边上的中点.若,,则平行四边形的周长是
.
10.如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足为E、F,若∠1=60°,
BE=2cm,DF=3cm,则AB=
,AD=
,平行四边形
ABCD的周长为
.
(第十题图)
(第十一题图)
(第十二题图)
11.如图,在矩形ABCD中,
E为AD的中点,∠BED的角平分线交BC于F.
若AB=6,BC=16,则FC的长度为_______.
12.如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为
.
三、作图题:(8分)
13.如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
四、解答题:(每题8分,共24分)
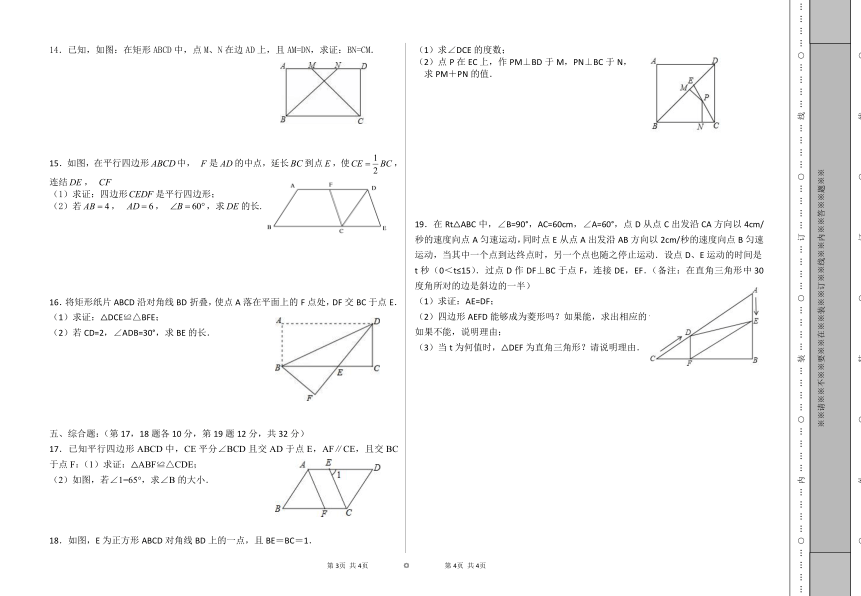
14.已知,如图:在矩形ABCD中,点M、N在边AD上,且AM=DN,求证:BN=CM.
15.如图,在平行四边形中,
是的中点,延长到点,使,连结,
(1)求证:四边形是平行四边形;
(2)若,
,
,求的长.
16.将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
五、综合题:(第17,18题各10分,第19题12分,共32分)
17.已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F:(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.
18.如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.
(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,
求PM+PN的值.
19.在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(备注:在直角三角形中30度角所对的边是斜边的一半)
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,
如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
2019—2020学年度第二学期八年级数学下册第三单元试卷
第十八章
平行四边形
(命题人:)
时间:100分钟
总分:100分
题号
一
二
三
四
五
总分
得分
一、选择题:(每题3分,共18分,请将答案填写在表格中)
题号
1
2
3
4
5
6
选项
C
A
B
D
C
D
二、填空题(每小题3分,共18分)
7、10cm
8、25度
9、12
10、4cm,6cm,20cm
11、6cm
12、
三、作图题:共8分
解:(1)正确画出点F,具体作法如下:
连接AC、BD相交于点O,连接EO并延长EO交AD于点F(或作射线EO交AD于点F.)
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OD=OB,
∴∠ADO=∠CBO,∠DFO=∠BEO,
∴△DFO≌△BEO,
∴DF=BE.
四、解答题:(每题8分,共24分)
14.∵AM=DN,∴AM+MN=MN+ND,∴AN=MD,∵四边形ABCD是矩形,
∴AB=CD,∠A=∠D,在△ABN和△DCM中,
∵,∴△ABN≌△DCM,∴BN=CM.
15.解:(1)证明:
在平行四边形ABCD中,
AD=BC,F为AD的中点
∴DF是AD的一半,
又∵CE是BC的一——
∴DF=CE,且DF∥CE。……
(4分)
∴四边形CEDF是平行四边形。
(2)如图,过点D作DH⊥BE于点H,
∴在Rt△DHE中,根据勾股定理,得
16
解:(1)∵AD∥BC,
∴∠ADB=∠DBC,
根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,
∴∠DBC=∠BDF,
∴BE=DE,
在△DCE和△BFE中,
,
∴△DCE≌△BFE;
(2)在Rt△BCD中,
∵CD=2,∠ADB=∠DBC=30°,
∴BC=2,
在Rt△BCD中,
∵CD=2,∠EDC=30°,
∴DE=2EC,
∴(2EC)2﹣EC2=CD2,
∴CE=,
∴BE=BC﹣EC=.
五、综合题:(第17,18题每题10分,第19题12分,共32分)
17.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∠B=∠D,
∴∠1=∠DCE,
∵AF∥CE,
∴∠AFB=∠ECB,
∵CE平分∠BCD,
∴∠DCE=∠ECB,
∴∠AFB=∠1,
在△ABF和△CDE中,,
∴△ABF≌△CDE(AAS);
(2)由(1)得:∠1=∠ECB,∠DCE=∠ECB,
∴∠1=∠DCE=65°,
∴∠B=∠D=180°﹣2×65°=50°.
18.
解:(1)在正方形ABCD中,∠BCD=90°,∠DBC=45°,
∵BE=BC,
∴AB=BE,
∴∠BCE=∠BEC=(180°-∠DBC)=67.5°,
∴∠DCE=∠DCB-∠BCE=90°-67.5°=22.5°,
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,
∵∠EBF=45°,
∴△BEF是等腰直角三角形,
∵BE=BC=1,
∴BF=EF=,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
即BE?PM+BC?PN=BC?EF,
∵BE=BC,
∴PM+PN=EF=.
19.解:(1)、∵在Rt△ABC中,∠C=90°﹣∠A=30°,
∴AB=AC=×60=30cm
∵CD=4t,AE=2t,
又∵在Rt△CDF中,∠C=30°,
∴DF=CD=2t
∴DF=AE
(2)、能。
∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形
当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10
∴当t=10时,AEFD是菱形
(3)、若△DEF为直角三角形,有两种情况:
①如图1,∠EDF=90°,DE∥BC,
则AD=2AE,即60﹣4t=2×2t,解得:t=。
②如图2,∠DEF=90°,DE⊥AC,
则AE=2AD,即2t=2(60-4t),解得:t=12。
综上所述,当t=或12时,△DEF为直角三角形
A
B
E
C
G
F
D
1
平行四边形单元测试
(
时间:100分钟
总分:100分)
题号
一
二
三
四
五
总分
得分
一、选择题:(每题3分,共18分,请将答案填写在表格中)
题号
1
2
3
4
5
6
选项
1.下列说法中错误的是( )
A.
平行四边形的对角线互相平分
B.
两组对边分别相等的四边形是平行四边形
C.
有一组邻边相等且有一个角是直角的四边形是正方形
D.
矩形的对角线相等
2.顺次连接一个矩形各边的中点,得到的四边形一定是(
)
A.菱形
B.矩形
C.正方形
D.梯形
3.已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,则此菱形的面积为(
)
A.48cm2
B.24cm2
C.18cm2
D.12cm2
4.如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
A.
∠ABC=90°
B.
AC=BD
C.
OA=OB
D.
OA=AD
5.如图,正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为(
)
A.
8
B.
C.
10
D.
6.如图,正方形ABCD中,E、F均为中点,则下列结论中:
7.①AF⊥DE;
②AD=BP;
③PE+PF=PC;
④PE+PF=PC。其中正确的是( )
A.①④
B.①②④
C.①③
D.①②③
二、填空题(每小题3分,共18分)
7.已知在Rt△ABC中,斜边上的中线=5cm,则斜边AB的长=___________.
8.如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,∠AOB=50°,
则∠BAE的度数是
.
(第八题图)
(第九题图)
9.如图,在平行四边形中,是边上的中点.若,,则平行四边形的周长是
.
10.如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足为E、F,若∠1=60°,
BE=2cm,DF=3cm,则AB=
,AD=
,平行四边形
ABCD的周长为
.
(第十题图)
(第十一题图)
(第十二题图)
11.如图,在矩形ABCD中,
E为AD的中点,∠BED的角平分线交BC于F.
若AB=6,BC=16,则FC的长度为_______.
12.如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为
.
三、作图题:(8分)
13.如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
四、解答题:(每题8分,共24分)
14.已知,如图:在矩形ABCD中,点M、N在边AD上,且AM=DN,求证:BN=CM.
15.如图,在平行四边形中,
是的中点,延长到点,使,连结,
(1)求证:四边形是平行四边形;
(2)若,
,
,求的长.
16.将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
五、综合题:(第17,18题各10分,第19题12分,共32分)
17.已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F:(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.
18.如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.
(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,
求PM+PN的值.
19.在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(备注:在直角三角形中30度角所对的边是斜边的一半)
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,
如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
2019—2020学年度第二学期八年级数学下册第三单元试卷
第十八章
平行四边形
(命题人:)
时间:100分钟
总分:100分
题号
一
二
三
四
五
总分
得分
一、选择题:(每题3分,共18分,请将答案填写在表格中)
题号
1
2
3
4
5
6
选项
C
A
B
D
C
D
二、填空题(每小题3分,共18分)
7、10cm
8、25度
9、12
10、4cm,6cm,20cm
11、6cm
12、
三、作图题:共8分
解:(1)正确画出点F,具体作法如下:
连接AC、BD相交于点O,连接EO并延长EO交AD于点F(或作射线EO交AD于点F.)
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OD=OB,
∴∠ADO=∠CBO,∠DFO=∠BEO,
∴△DFO≌△BEO,
∴DF=BE.
四、解答题:(每题8分,共24分)
14.∵AM=DN,∴AM+MN=MN+ND,∴AN=MD,∵四边形ABCD是矩形,
∴AB=CD,∠A=∠D,在△ABN和△DCM中,
∵,∴△ABN≌△DCM,∴BN=CM.
15.解:(1)证明:
在平行四边形ABCD中,
AD=BC,F为AD的中点
∴DF是AD的一半,
又∵CE是BC的一——
∴DF=CE,且DF∥CE。……
(4分)
∴四边形CEDF是平行四边形。
(2)如图,过点D作DH⊥BE于点H,
∴在Rt△DHE中,根据勾股定理,得
16
解:(1)∵AD∥BC,
∴∠ADB=∠DBC,
根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,
∴∠DBC=∠BDF,
∴BE=DE,
在△DCE和△BFE中,
,
∴△DCE≌△BFE;
(2)在Rt△BCD中,
∵CD=2,∠ADB=∠DBC=30°,
∴BC=2,
在Rt△BCD中,
∵CD=2,∠EDC=30°,
∴DE=2EC,
∴(2EC)2﹣EC2=CD2,
∴CE=,
∴BE=BC﹣EC=.
五、综合题:(第17,18题每题10分,第19题12分,共32分)
17.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∠B=∠D,
∴∠1=∠DCE,
∵AF∥CE,
∴∠AFB=∠ECB,
∵CE平分∠BCD,
∴∠DCE=∠ECB,
∴∠AFB=∠1,
在△ABF和△CDE中,,
∴△ABF≌△CDE(AAS);
(2)由(1)得:∠1=∠ECB,∠DCE=∠ECB,
∴∠1=∠DCE=65°,
∴∠B=∠D=180°﹣2×65°=50°.
18.
解:(1)在正方形ABCD中,∠BCD=90°,∠DBC=45°,
∵BE=BC,
∴AB=BE,
∴∠BCE=∠BEC=(180°-∠DBC)=67.5°,
∴∠DCE=∠DCB-∠BCE=90°-67.5°=22.5°,
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,
∵∠EBF=45°,
∴△BEF是等腰直角三角形,
∵BE=BC=1,
∴BF=EF=,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
即BE?PM+BC?PN=BC?EF,
∵BE=BC,
∴PM+PN=EF=.
19.解:(1)、∵在Rt△ABC中,∠C=90°﹣∠A=30°,
∴AB=AC=×60=30cm
∵CD=4t,AE=2t,
又∵在Rt△CDF中,∠C=30°,
∴DF=CD=2t
∴DF=AE
(2)、能。
∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形
当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10
∴当t=10时,AEFD是菱形
(3)、若△DEF为直角三角形,有两种情况:
①如图1,∠EDF=90°,DE∥BC,
则AD=2AE,即60﹣4t=2×2t,解得:t=。
②如图2,∠DEF=90°,DE⊥AC,
则AE=2AD,即2t=2(60-4t),解得:t=12。
综上所述,当t=或12时,△DEF为直角三角形
A
B
E
C
G
F
D
1
