上海市卢湾、黄浦区2012届九年级上学期期末质量调研考试(数学)WORD版有答案
文档属性
| 名称 | 上海市卢湾、黄浦区2012届九年级上学期期末质量调研考试(数学)WORD版有答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 245.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-20 00:00:00 | ||
图片预览


文档简介
卢湾、黄浦区2011学年第一学期期末考试
九年级数学试卷
(时间100分钟,满分150分) 2012.1
(本试卷所有答案请书写在答题卷规定位置上)
一、选择题(本大题共6题,每题4分,满分24分)
1.若,则的大小是…………………………………( )
(A); (B); (C) ; (D).
2.若∽,顶点、、分别与、、对应,且,则这两个三角形的面积比为…………………………( )
(A); (B); (C); (D).
3.若在同一直角坐标系中,作,,的图像,则它们……………………………………………………………………( )
(A)都关于轴对称; (B)开口方向相同;
(C)都经过原点; (D)互相可以通过平移得到.
4.对于函数,下列结论正确的是………………( )
(A)在直线的左侧部分函数的图像是上升的;
(B)在直线的右侧部分函数的图像是上升的;
(C)在直线的左侧部分函数的图像是上升的;
(D)在直线的右侧部分函数的图像是上升的.
5.已知矩形的对角线、相交于点,若,,则( )
(A); (B);
(C); (D).
6.如果点、分别在的边和上,那么不能判定∥的比例式是………………………………………………………………( )
(A); (B);
(C); (D).
二、填空题(本大题共12题,每题4分,满分48分)
7.计算: .
8.计算: .
9.如果先将抛物线向左平移3个单位,再向下平移1个单位,那么所得到的抛物线的表达式为__________.
10.如果在某建筑物的处测得目标的俯角为,那么从目标可以测得这个建筑物的处的仰角为 .
11.抛物线的最低点坐标是 .
12. 若在比例尺为的地图上,测得两地的距离为5cm,则这两地的实际距离是 km.
13.传送带和地面所成斜坡的坡度为,它把物体从地面送到离地面高8米的地方,物体在传送带上所经过的路程为 米.
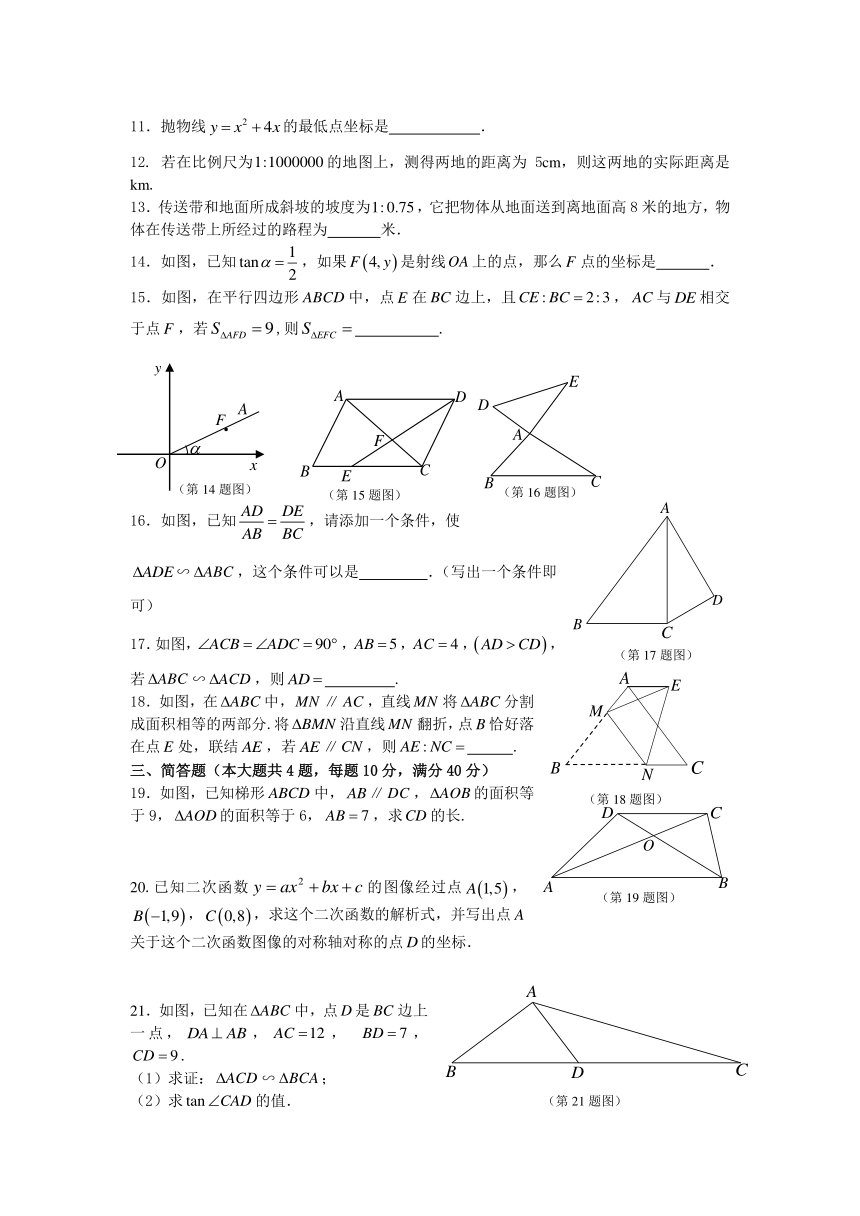
14.如图,已知,如果是射线上的点,那么点的坐标是 .
15.如图,在平行四边形中,点在边上,且,与相交于点,若,则 .
16.如图,已知,请添加一个条件,使
∽,这个条件可以是 .(写出一个条件即可)
17.如图,,,,,若∽,则 .
18.如图,在中,∥,直线将分割成面积相等的两部分.将沿直线翻折,点恰好落在点处,联结,若∥,则 .
三、简答题(本大题共4题,每题10分,满分40分)
19.如图,已知梯形中,∥,的面积等于9,的面积等于6,,求的长.
20.已知二次函数的图像经过点,,,求这个二次函数的解析式,并写出点关于这个二次函数图像的对称轴对称的点的坐标.
21.如图,已知在中,点是边上一点,,, ,.
(1)求证:∽;
(2)求的值.
22.如图,已知点在上,且,点是延长线上一点,,联结与交于点,求的值.
四、解答题(本大题共2题,每题12分,满分24分)
23.一艘轮船自南向北航行,在处测得北偏东方向有一座小岛,继续向北航行60海里到达处,测得小岛此时在轮船的北偏东63.5°方向上.之后,轮船继续向北航行约多少海里,距离小岛最近?
(参考数据:,, ,)
24.已知在平面直角坐标系中,抛物线与轴相交于,两点,对称轴与轴相交于点,顶点为点,且的正切值为.
求顶点的坐标;
求抛物线的表达式;
点是抛物线上的一点,且位于第一象限,联结,若,求点的坐标.
五、(本题满分14分)
25.在矩形中,,,是边上一点,交于点,过点作,交射线于点,交射线于点.
(1)如图a,当点与点重合时,求的长;
(2)如图b,当点在线段上时,设,,求与之间的函数关系式,并写出它的定义域;
(3)联结,当与相似时,求线段的长.
卢湾、黄浦区区2011学年第一学期期末考试九年级数学试卷
参考答案及评分说明
一、选择题(本大题共6题,每题4分,满分24分)
1.A; 2. D; 3.A; 4.D; 5. B; 6.C.
二、填空题(本大题共12题,每题4分,满分48分)
7.; 8.; 9.; 10.37;11.;
12.50; 13.10; 14.; 15.4; 16.等; 17.;18..
三、简答题(本大题共4题,每题10分,满分40分)
19. 解:∵∥,∴,………………………………(3分)
∵的面积等于9,的面积等于6,∴,(3分)
∴,………………………………………………………(2分)
∵,∴,∴.…………………………………(2分)
20. 解:由题意可得, 解,得……………(6分)
所以,……………………………………………………(1分)
点关于这个二次函数图像的对称轴对称的点的坐标是.…(3分)
21.(1)证明:∵,,∴,…………………(1分)
∵,∴,,∴,…………………(3分)
∵,∴∽.………………………………………(2分)
(2)∵∽,∴,,………(2分)
∵,∴,∴.………………(2分)
22.解:过点作∥,交于点.…………………………(1分)
∴,……………………………………………………………(2分)
∵,∴,…………………………………………(1分)
∴,∴,………………………………………………(2分)
又∵,∴,……………………………………(2分)
∵∥,∴.………………………………(2分)
四、解答题(本大题共2题,每题12分,满分24分)
23.解:过点作的垂线,垂足为点.…………………………(1分)
设,在Rt中,,…………(1分)
∴.……………………………………………………(2分)
在Rt中, ,……………………………(1分)
∵,……………………………………………(1分)
∴.……………………………………………(2分)
∴,∵,,(2分)
解,得 .…………………………………………………………(1分)
答:轮船继续向东航行约15海里,距离小岛C最近. ………………(1分)
24. 解:(1)∵抛物线与轴相交于,两点,
∴对称轴:直线,;……………………………………(2分)
∵,,
∴,∵,∴.……………………………………(2分)
(2)设,………………………………………………(2分)
将代入上式,得,,…………………………………(1分)
所以,这条抛物线的表达为. …………………………(1分)
(3)过点作轴,垂足为点.……………………………(1分)
设,∵,∴,
∵,∴,…………………………(1分)
∵,,∴,………………(1分)
解,得,(舍),∴.…………………………(1分)
五、(本题满分14分)
25.(1)∵,∴,……………………(1分)
∵,∴……………………………………(1分)
∵,∴,∵,∴.…………………(1分)
(2)过点作,垂足为点.………………………………(1分)
∴,∵∥,∴,,
∵,∴,∴,………………(1分)
∴,……………………………………………………(1分)
∵,,,∴.……(2分)
(3)∵,∴,
∵ ,∴,
∴,∴.………………………………(2分)
当与相似时,
ⅰ)若,
∵,,∴,∴,
∴,∴,∴,∴…(2分)
ⅱ)若,如所示,记与交于点.
∵,, ∴,
∵∥,∴,∴,
∴,∴,
设,则,
∴,∴,
∴,,∴………(2分)
综上所述,线段的长为或1.
(以上各题如有其他方法,请参照评分标准酌情给分)
(第14题图)
·
(第16题图)
(第15题图)
(第17题图)
(第18题图)
(第19题图)
(第21题图)
(第22题图)
(第23题图)
北
东
x
y
O
(第24题图)
(备用图)
(第25题图b)
(第25题图a)
F(H)
图1
九年级数学试卷
(时间100分钟,满分150分) 2012.1
(本试卷所有答案请书写在答题卷规定位置上)
一、选择题(本大题共6题,每题4分,满分24分)
1.若,则的大小是…………………………………( )
(A); (B); (C) ; (D).
2.若∽,顶点、、分别与、、对应,且,则这两个三角形的面积比为…………………………( )
(A); (B); (C); (D).
3.若在同一直角坐标系中,作,,的图像,则它们……………………………………………………………………( )
(A)都关于轴对称; (B)开口方向相同;
(C)都经过原点; (D)互相可以通过平移得到.
4.对于函数,下列结论正确的是………………( )
(A)在直线的左侧部分函数的图像是上升的;
(B)在直线的右侧部分函数的图像是上升的;
(C)在直线的左侧部分函数的图像是上升的;
(D)在直线的右侧部分函数的图像是上升的.
5.已知矩形的对角线、相交于点,若,,则( )
(A); (B);
(C); (D).
6.如果点、分别在的边和上,那么不能判定∥的比例式是………………………………………………………………( )
(A); (B);
(C); (D).
二、填空题(本大题共12题,每题4分,满分48分)
7.计算: .
8.计算: .
9.如果先将抛物线向左平移3个单位,再向下平移1个单位,那么所得到的抛物线的表达式为__________.
10.如果在某建筑物的处测得目标的俯角为,那么从目标可以测得这个建筑物的处的仰角为 .
11.抛物线的最低点坐标是 .
12. 若在比例尺为的地图上,测得两地的距离为5cm,则这两地的实际距离是 km.
13.传送带和地面所成斜坡的坡度为,它把物体从地面送到离地面高8米的地方,物体在传送带上所经过的路程为 米.
14.如图,已知,如果是射线上的点,那么点的坐标是 .
15.如图,在平行四边形中,点在边上,且,与相交于点,若,则 .
16.如图,已知,请添加一个条件,使
∽,这个条件可以是 .(写出一个条件即可)
17.如图,,,,,若∽,则 .
18.如图,在中,∥,直线将分割成面积相等的两部分.将沿直线翻折,点恰好落在点处,联结,若∥,则 .
三、简答题(本大题共4题,每题10分,满分40分)
19.如图,已知梯形中,∥,的面积等于9,的面积等于6,,求的长.
20.已知二次函数的图像经过点,,,求这个二次函数的解析式,并写出点关于这个二次函数图像的对称轴对称的点的坐标.
21.如图,已知在中,点是边上一点,,, ,.
(1)求证:∽;
(2)求的值.
22.如图,已知点在上,且,点是延长线上一点,,联结与交于点,求的值.
四、解答题(本大题共2题,每题12分,满分24分)
23.一艘轮船自南向北航行,在处测得北偏东方向有一座小岛,继续向北航行60海里到达处,测得小岛此时在轮船的北偏东63.5°方向上.之后,轮船继续向北航行约多少海里,距离小岛最近?
(参考数据:,, ,)
24.已知在平面直角坐标系中,抛物线与轴相交于,两点,对称轴与轴相交于点,顶点为点,且的正切值为.
求顶点的坐标;
求抛物线的表达式;
点是抛物线上的一点,且位于第一象限,联结,若,求点的坐标.
五、(本题满分14分)
25.在矩形中,,,是边上一点,交于点,过点作,交射线于点,交射线于点.
(1)如图a,当点与点重合时,求的长;
(2)如图b,当点在线段上时,设,,求与之间的函数关系式,并写出它的定义域;
(3)联结,当与相似时,求线段的长.
卢湾、黄浦区区2011学年第一学期期末考试九年级数学试卷
参考答案及评分说明
一、选择题(本大题共6题,每题4分,满分24分)
1.A; 2. D; 3.A; 4.D; 5. B; 6.C.
二、填空题(本大题共12题,每题4分,满分48分)
7.; 8.; 9.; 10.37;11.;
12.50; 13.10; 14.; 15.4; 16.等; 17.;18..
三、简答题(本大题共4题,每题10分,满分40分)
19. 解:∵∥,∴,………………………………(3分)
∵的面积等于9,的面积等于6,∴,(3分)
∴,………………………………………………………(2分)
∵,∴,∴.…………………………………(2分)
20. 解:由题意可得, 解,得……………(6分)
所以,……………………………………………………(1分)
点关于这个二次函数图像的对称轴对称的点的坐标是.…(3分)
21.(1)证明:∵,,∴,…………………(1分)
∵,∴,,∴,…………………(3分)
∵,∴∽.………………………………………(2分)
(2)∵∽,∴,,………(2分)
∵,∴,∴.………………(2分)
22.解:过点作∥,交于点.…………………………(1分)
∴,……………………………………………………………(2分)
∵,∴,…………………………………………(1分)
∴,∴,………………………………………………(2分)
又∵,∴,……………………………………(2分)
∵∥,∴.………………………………(2分)
四、解答题(本大题共2题,每题12分,满分24分)
23.解:过点作的垂线,垂足为点.…………………………(1分)
设,在Rt中,,…………(1分)
∴.……………………………………………………(2分)
在Rt中, ,……………………………(1分)
∵,……………………………………………(1分)
∴.……………………………………………(2分)
∴,∵,,(2分)
解,得 .…………………………………………………………(1分)
答:轮船继续向东航行约15海里,距离小岛C最近. ………………(1分)
24. 解:(1)∵抛物线与轴相交于,两点,
∴对称轴:直线,;……………………………………(2分)
∵,,
∴,∵,∴.……………………………………(2分)
(2)设,………………………………………………(2分)
将代入上式,得,,…………………………………(1分)
所以,这条抛物线的表达为. …………………………(1分)
(3)过点作轴,垂足为点.……………………………(1分)
设,∵,∴,
∵,∴,…………………………(1分)
∵,,∴,………………(1分)
解,得,(舍),∴.…………………………(1分)
五、(本题满分14分)
25.(1)∵,∴,……………………(1分)
∵,∴……………………………………(1分)
∵,∴,∵,∴.…………………(1分)
(2)过点作,垂足为点.………………………………(1分)
∴,∵∥,∴,,
∵,∴,∴,………………(1分)
∴,……………………………………………………(1分)
∵,,,∴.……(2分)
(3)∵,∴,
∵ ,∴,
∴,∴.………………………………(2分)
当与相似时,
ⅰ)若,
∵,,∴,∴,
∴,∴,∴,∴…(2分)
ⅱ)若,如所示,记与交于点.
∵,, ∴,
∵∥,∴,∴,
∴,∴,
设,则,
∴,∴,
∴,,∴………(2分)
综上所述,线段的长为或1.
(以上各题如有其他方法,请参照评分标准酌情给分)
(第14题图)
·
(第16题图)
(第15题图)
(第17题图)
(第18题图)
(第19题图)
(第21题图)
(第22题图)
(第23题图)
北
东
x
y
O
(第24题图)
(备用图)
(第25题图b)
(第25题图a)
F(H)
图1
同课章节目录
