数学人教A版(2019)必修第二册8.5 空间直线、平面的平行(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.5 空间直线、平面的平行(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 595.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 15:48:59 | ||
图片预览






文档简介
(共20张PPT)
第8章
立体几何初步
8.5
空间直线、平面的平行(1)
直线与直线平行
1
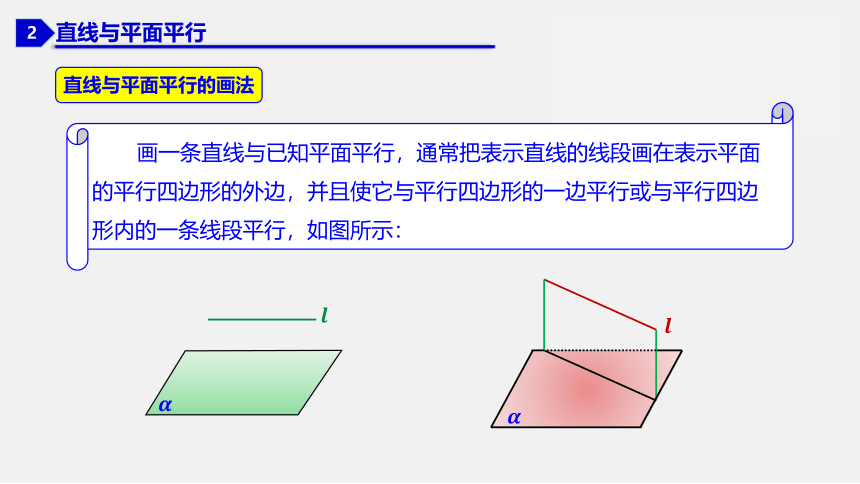
平行于同一条直线的两条直线互相平行.
基本事实④(平行线的传递性)
图形语言:
符号语言://
////
应用:判定与证明空间中两条直线平行.
【1】平行公理:过直线外一点有且
只有一条直线与已知直线平行.
相关知识回顾
【2】平行线的性质:在同一平面内,
如果两条直线都和第三条直线
平行,那么这两条直线也互相
平行.
直线与直线平行
1
顺次连接不共面的四点A,B,C,D所构成的图形叫做空间四边形,如图中的四边形表示空间四边形ABCD.
点A,B,C,D叫做空间四边形的顶点;所连接的相邻顶点间的线段叫做空间四边形的边,如图中的AB,BC,CD,DA.连接不相邻的顶点的线段叫做空间四边形的对角线,如图中的线段BD,AC,空间四边形的对角线不共面.
空间四边形
直线与直线平行
1
如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
等角定理
图形语言:
符号语言:////
应用:判定与证明两个角相等
直线与直线平行
1
等角定理
如果一个角的两边与另一个角的两边分别对应平行,并且一组对应边的方向相同,另一组对应边的方向相反,那么这两个角互补.
如果一个角的两边与另一个角的两边分别对应平行,并且方向相反,那么这两个角相等
如果两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形的关系是(
)
A.
全等
B.
相似
C.仅有一个角相等
D.
三个角都不相等
直线与平面平行
2
直线与平面平行的判定定理
如果平面外一条直线与此平面内一条直线平行,那么该直线与此平面平行
图形语言:
符号语言:
定理应用:线线平行
线面平行
定理的证明方法:反证法
证明:假设与不平行,∵,∴与相交,设,则否则与//矛盾.过点在内作直线,使//,则//.又,即与//矛盾,∴假设不成立,∴.
直线与平面平行
2
直线与平面平行的判定定理
用判定定理判定直线
和平面
平行的必备条件:
直线
在平面
外,即
;
直线
在平面
外,即
;
直线
平行,即
//.
判定定理体现了等价转化思想,将“线面平行问题”转化为“线线平行问题”,这也是处理空间位置关系的一种常用方法,即把空间问题转化为平面问题.
直线与平面平行
2
直线与平面平行的画法
画一条直线与已知平面平行,通常把表示直线的线段画在表示平面的平行四边形的外边,并且使它与平行四边形的一边平行或与平行四边形内的一条线段平行,如图所示:
直线与平面平行
2
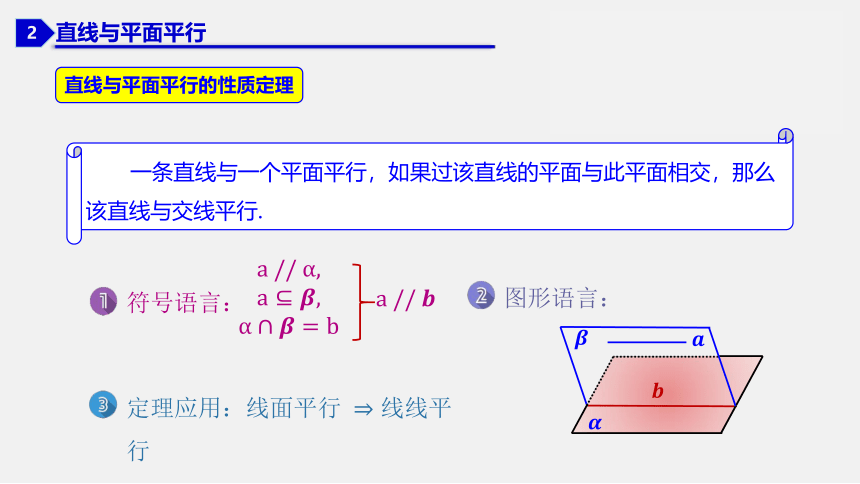
直线与平面平行的性质定理
一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
图形语言:
符号语言:
定理应用:线面平行
线线平行
直线与平面平行
2
直线与平面平行的性质定理
若,在平面
内找到一条直线
,使得
//
的作法:经过已知直线
作一个平面与已知平面
相交,则交线和已知直线
平行,此交线就是要找的直线
(有无数条)
性质定理可以作为直线与直线平行的判定方法
该定理中有三个条件:.这三个条件缺一不可
平面
内凡是不与
平行的直线,都与
异面
直线与平面平行
2
直线与平面平行的性质定理
直线
//平面,
内有条
直线相交于一点,则这
条直线中与直线
平行的直线一共有(
)条
A.
0
B.
1
C.
0
或
1
D.
无数
【解析】过直线
和
条直线的交点作平面
,设平面
与交于直线
,则//.若所给
条直线中有一条直线是与
重合的,则此直线与直线
平行;若没有与
重合的直线,则与直线
平行的直线有0条.
平面与平面平行
3
平面与平面平行的判定定理及推论
【两个平面平行的判定定理】如果一个平面内的两条相交直线与另一个平
面平行,那么这两个平面平行.
图形语言:
符号语言:
平面与平面平行
3
平面与平面平行的判定定理及推论
【两个平面平行的判定定理】如果一个平面内的两条相交直线与另一个平
面平行,那么这两个平面平行.
定理应用:线面平行
面面平行
证明方法:反证法
证明:假设
与不平行,则
与
必相交,记
∩,则
.
∵
∴
与
无公共点.
∵
∴
∴
这与已知
矛盾,∴假设不成立,∴
平面与平面平行
3
平面与平面平行的判定定理及推论
要证明面面平行,由平面与平面平行的判定定理知,需在一平面内寻找两条相交且与另一平面平行的直线,要证明线面平行,需根据直线与平面平行的判定定理,在平面内找与已知直线平行的直线
判定两个平面平行与判定线面平行一样,应遵循“先找后作”的原则,即先在一个平面内找到两条与另一个平面平行的相交直线,若找不到再做辅助线
平面与平面平行
3
平面与平面平行的判定定理及推论
【两个平面平行的判定定理的推论】如果一个平面内有两条相交直线分别
平行于另一个平面内的两条直线,那么这两个平面平行.
图形语言:
符号语言:
平面与平面平行
3
平面与平面平行的判定定理及推论
【两个平面平行的判定定理的推论】如果一个平面内有两条相交直线分别
平行于另一个平面内的两条直线,那么这两个平面平行.
两个平面平行的画法:通常把表示两个平行平面的平行四边形的相邻两边分别画成平行线,如图:
平面与平面平行
3
平面与平面平行的性质定理
【平面与平面平行的性质定理】两个平面平行,如果另一个平面与这两个
平面相交,则交线平行.
图形语言:
符号语言:
定理应用:面面平行
线线平行
平面与平面平行
3
平面与平面平行的性质定理
已知两个平面平行,虽然一个平面内的任意一条直线都平行于另一个平面,但是一个平面内的一条直线与另一个平面内的一条直线不一定互相平行,它们可能是平行直线,也可能是异面直线,但不可能是相交直线
该定理中有三个条件:这三个条件缺一不可
该定理提供了证明线线平行的一种方法,应用时要紧扣“两个平行平面同时和第三个平面相交”这个条件
平面与平面平行
3
平面与平面平行的性质定理
【两平面平行的相关性质】
夹在两个平行平面内的两条平行线段相等
若两个平面平行,则一个平面内的任意一条直线都和另一个平面平行.
符号语言:
平行平面具有传递性,即平行于同一个平面的两个平面平行.
符号语言:
两条直线被三个平行平面所截,截得的对应线段成比例.
THANKS
“
”
第8章
立体几何初步
8.5
空间直线、平面的平行(1)
直线与直线平行
1
平行于同一条直线的两条直线互相平行.
基本事实④(平行线的传递性)
图形语言:
符号语言://
////
应用:判定与证明空间中两条直线平行.
【1】平行公理:过直线外一点有且
只有一条直线与已知直线平行.
相关知识回顾
【2】平行线的性质:在同一平面内,
如果两条直线都和第三条直线
平行,那么这两条直线也互相
平行.
直线与直线平行
1
顺次连接不共面的四点A,B,C,D所构成的图形叫做空间四边形,如图中的四边形表示空间四边形ABCD.
点A,B,C,D叫做空间四边形的顶点;所连接的相邻顶点间的线段叫做空间四边形的边,如图中的AB,BC,CD,DA.连接不相邻的顶点的线段叫做空间四边形的对角线,如图中的线段BD,AC,空间四边形的对角线不共面.
空间四边形
直线与直线平行
1
如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
等角定理
图形语言:
符号语言:////
应用:判定与证明两个角相等
直线与直线平行
1
等角定理
如果一个角的两边与另一个角的两边分别对应平行,并且一组对应边的方向相同,另一组对应边的方向相反,那么这两个角互补.
如果一个角的两边与另一个角的两边分别对应平行,并且方向相反,那么这两个角相等
如果两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形的关系是(
)
A.
全等
B.
相似
C.仅有一个角相等
D.
三个角都不相等
直线与平面平行
2
直线与平面平行的判定定理
如果平面外一条直线与此平面内一条直线平行,那么该直线与此平面平行
图形语言:
符号语言:
定理应用:线线平行
线面平行
定理的证明方法:反证法
证明:假设与不平行,∵,∴与相交,设,则否则与//矛盾.过点在内作直线,使//,则//.又,即与//矛盾,∴假设不成立,∴.
直线与平面平行
2
直线与平面平行的判定定理
用判定定理判定直线
和平面
平行的必备条件:
直线
在平面
外,即
;
直线
在平面
外,即
;
直线
平行,即
//.
判定定理体现了等价转化思想,将“线面平行问题”转化为“线线平行问题”,这也是处理空间位置关系的一种常用方法,即把空间问题转化为平面问题.
直线与平面平行
2
直线与平面平行的画法
画一条直线与已知平面平行,通常把表示直线的线段画在表示平面的平行四边形的外边,并且使它与平行四边形的一边平行或与平行四边形内的一条线段平行,如图所示:
直线与平面平行
2
直线与平面平行的性质定理
一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
图形语言:
符号语言:
定理应用:线面平行
线线平行
直线与平面平行
2
直线与平面平行的性质定理
若,在平面
内找到一条直线
,使得
//
的作法:经过已知直线
作一个平面与已知平面
相交,则交线和已知直线
平行,此交线就是要找的直线
(有无数条)
性质定理可以作为直线与直线平行的判定方法
该定理中有三个条件:.这三个条件缺一不可
平面
内凡是不与
平行的直线,都与
异面
直线与平面平行
2
直线与平面平行的性质定理
直线
//平面,
内有条
直线相交于一点,则这
条直线中与直线
平行的直线一共有(
)条
A.
0
B.
1
C.
0
或
1
D.
无数
【解析】过直线
和
条直线的交点作平面
,设平面
与交于直线
,则//.若所给
条直线中有一条直线是与
重合的,则此直线与直线
平行;若没有与
重合的直线,则与直线
平行的直线有0条.
平面与平面平行
3
平面与平面平行的判定定理及推论
【两个平面平行的判定定理】如果一个平面内的两条相交直线与另一个平
面平行,那么这两个平面平行.
图形语言:
符号语言:
平面与平面平行
3
平面与平面平行的判定定理及推论
【两个平面平行的判定定理】如果一个平面内的两条相交直线与另一个平
面平行,那么这两个平面平行.
定理应用:线面平行
面面平行
证明方法:反证法
证明:假设
与不平行,则
与
必相交,记
∩,则
.
∵
∴
与
无公共点.
∵
∴
∴
这与已知
矛盾,∴假设不成立,∴
平面与平面平行
3
平面与平面平行的判定定理及推论
要证明面面平行,由平面与平面平行的判定定理知,需在一平面内寻找两条相交且与另一平面平行的直线,要证明线面平行,需根据直线与平面平行的判定定理,在平面内找与已知直线平行的直线
判定两个平面平行与判定线面平行一样,应遵循“先找后作”的原则,即先在一个平面内找到两条与另一个平面平行的相交直线,若找不到再做辅助线
平面与平面平行
3
平面与平面平行的判定定理及推论
【两个平面平行的判定定理的推论】如果一个平面内有两条相交直线分别
平行于另一个平面内的两条直线,那么这两个平面平行.
图形语言:
符号语言:
平面与平面平行
3
平面与平面平行的判定定理及推论
【两个平面平行的判定定理的推论】如果一个平面内有两条相交直线分别
平行于另一个平面内的两条直线,那么这两个平面平行.
两个平面平行的画法:通常把表示两个平行平面的平行四边形的相邻两边分别画成平行线,如图:
平面与平面平行
3
平面与平面平行的性质定理
【平面与平面平行的性质定理】两个平面平行,如果另一个平面与这两个
平面相交,则交线平行.
图形语言:
符号语言:
定理应用:面面平行
线线平行
平面与平面平行
3
平面与平面平行的性质定理
已知两个平面平行,虽然一个平面内的任意一条直线都平行于另一个平面,但是一个平面内的一条直线与另一个平面内的一条直线不一定互相平行,它们可能是平行直线,也可能是异面直线,但不可能是相交直线
该定理中有三个条件:这三个条件缺一不可
该定理提供了证明线线平行的一种方法,应用时要紧扣“两个平行平面同时和第三个平面相交”这个条件
平面与平面平行
3
平面与平面平行的性质定理
【两平面平行的相关性质】
夹在两个平行平面内的两条平行线段相等
若两个平面平行,则一个平面内的任意一条直线都和另一个平面平行.
符号语言:
平行平面具有传递性,即平行于同一个平面的两个平面平行.
符号语言:
两条直线被三个平行平面所截,截得的对应线段成比例.
THANKS
“
”
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
