三角函数的图像和性质
图片预览



文档简介
三角函数的图象和性质(一)
教学目标:
了解正弦、余弦、正切、余切函数的图象的画法,会用“五点法”画正弦、余弦函数和函数的简图;
理解的物理意义,掌握由函数的图象到函数的图象的变换原理;
掌握正弦、余弦、正切函数图象的对称轴或对称中心.
教学重点:函数的图象到函数的图象的变换方法.
一、知识点归纳:
“五点法”画正弦、余弦函数和函数的简图.
函数的图象到函数的图象的两种主要途径.
掌握正弦、余弦、正切函数图象的对称轴或对称中心.
会由三角函数图象求出相应的解析式.
二、知识点解析:
“五点法”画正弦、余弦函数和函数的简图,五个特殊点通常都是取三个平衡点,一个最高、一个最低点;
给出图象求的解析式的难点在于的确定,本质为待定系数法,基本方法是:①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到的,通常可由平衡点或最值点确定周期,进而确定.
对称性:函数对称轴可由解出;对称
中心的横坐标是方程的解,对称中心的纵坐标为.( 即整体代换法)
函数对称轴可由解出;对称中心的纵坐标是方程的解,对称中心的横坐标为.( 即整体代换法)
函数对称中心的横坐标可由解出,对称中心的纵坐标为,函数不具有轴对称性.
时,,当时,有最大值,
当时,有最小值;时,与上述情况相反.
(三)典例分析:
问题1. 已知函数.
用“五点法”画出它的图象;求它的振幅、周期和初相;
说明该函数的图象可由的图象经过怎样的变换而得到.
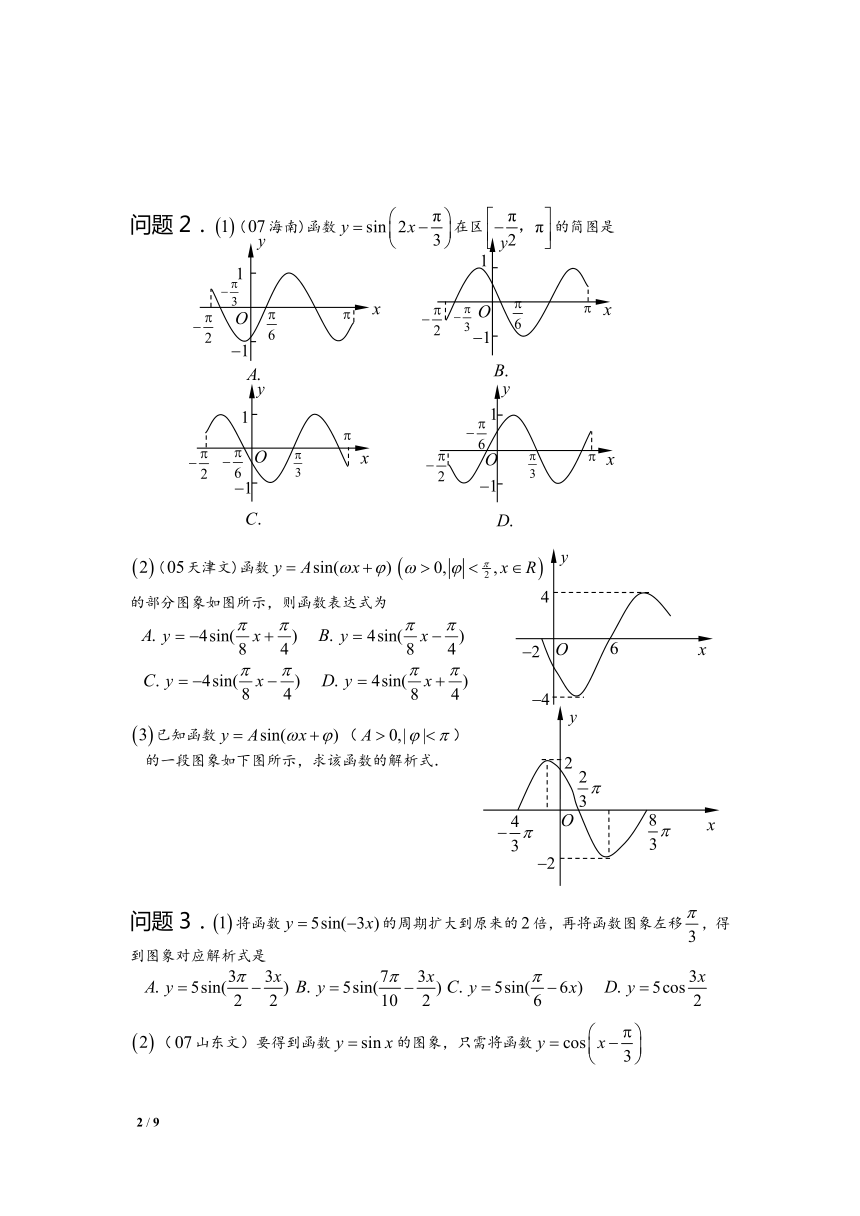
问题2. (
)(海南)函数在区的简图是
(天津文)函数
的部分图象如图所示,则函数表达式为
已知函数()
的一段图象如下图所示,求该函数的解析式.
问题3.将函数的周期扩大到原来的倍,再将函数图象左移,得到图象对应解析式是
(山东文)要得到函数的图象,只需将函数
的图象 向右平移个单位;向右平移个单位;
向左平移个单位;向左平移个单位
(山东)为了得到函数的图象,可以将函数的图象
向右平移个单位长度 向右平移个单位长度
向左平移个单位长度 向左平移个单位长度
问题4.(福建)已知函数的最小正周期为,则
该函数的图象 关于点对称 关于直线对称
关于点对称 .关于直线对称
(山东)已知函数,则下列判断正确的是
此函数的最小正周期为,其图象的一个对称中心是
此函数的最小正周期为,其图象的一个对称中心是
此函数的最小正周期为,其图象的一个对称中心是
此函数的最小正周期为,其图象的一个对称中心是
问题5.(陕西)设函数,其中向量,,,且的图象经过点.(Ⅰ)求实数的值;(Ⅱ)求函数的最小值及此时值的集合.
(四)课外作业:
要得到的图象,只需将的图象
向左平移 向右平移 向左平移 向右平移
如果函数的图象关于直线对称,则
(五)走向高考:
(天津)要得到函数的图象,只需将函数的
图象上所有的点的
横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度
横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度
横坐标伸长到原来的倍(纵坐标不变),再向左平行移动个单位长度
横坐标伸长到原来的倍(纵坐标不变),再向右平行移动个单位长度
(江苏)为了得到函数的图像,只需把函数的图像上所有的点
向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
向右平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
向左平移个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变)
向右平移个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变)
(安徽)函数的图象为,
①图象关于直线对称;②函数在区间内是增函数;
③由的图象向右平移个单位长度可以得到图象.
以上三个论断中,正确论断的个数是
(安徽)将函数的图象按向量
平移,平移后的图象如图所示,
则平移后的图象所对应函数的解析式是
(福建)函数,
)的部分图象如图,则
(福建)已知函数的最小正周期为,则该函数的图象
关于点对称关于直线对称关于点对称关于直线对称
(广东文)已知简谐运动的图象经过点,则该简谐运动的最小正周期和初相分别为
,;,;,;,
(陕西)已知函数
(Ⅰ)求函数的最小正周期;(Ⅱ)求使函数取得最大值的集合.
(全国Ⅰ文)设函数图像的一条对称轴是直线.(Ⅰ)求;(Ⅱ)求函数的单调增区间;
(Ⅲ)画出函数在区间上的图像。
(全国)已知函数是上的偶函数,其图象关于点对称,且在区间上是单调函数。求的值。
三角函数的图象和性质(二)
教学目标:掌握三角函数的定义域、值域的求法;理解周期函数与最小正周期的意义,会求经过简单的恒等变形可化为或的三角函数的周期.
教学重点:求三角函数的定义域是研究其它一切性质的前提.
(一)知识点归纳:
三角函数的定义域、值域及周期如下表:
函数 定义域 值域 周期
(二)知识点解析:
求三角函数的定义域实质就是解三角不等式(组).一般可用三角函数的图象或三角函数线确定三角不等式的解.列三角不等式,既要考虑分式的分母不能为零;偶次方根被开方数大于等于零;对数的真数大于零及底数大于零且不等于1,又要考虑三角函数本身的定义域;
求三角函数的值域的常用方法:①化为求代数函数的值域;②化为求的值域;③化为关于(或)的二次函数式;
三角函数的周期问题一般将函数式化为(其中为三角函数,).
(三)典例分析:
问题1. 求下列函数的定义域:
; ;
问题2.求下列函数的值域:
;;;.
问题3.求下列函数的周期:
;;
问题4.已知函数的定义域为,值域为,求常数的值.
(四)课后作业:
求函数的定义域.
函数的定义域为
若方程有解,则
(江西)设函数,则为( )
周期函数,最小正周期为 周期函数,最小正周期为
周期函数,数小正周期为 非周期函数
(全国Ⅱ)函数的最小正周期是 2
函数的最小正周期为
函数的周期是
已知函数,求的定义域,判断它的奇偶性,并求其值域
(五)走向高考:
(四川)函数的最小正周期为
(上海)函数的最小正周期
(福建)已知函数在区间上的最小值是,则
的最小值等于
(安徽文)解不等式.
(天津)已知函数,.
(Ⅰ)求函数的最小正周期;
(Ⅱ)求函数在区间上的最小值和最大值.
(重庆)设.(Ⅰ)求的最大值及最小正周期;
(Ⅱ)若锐角满足,求的值.
8 / 8
教学目标:
了解正弦、余弦、正切、余切函数的图象的画法,会用“五点法”画正弦、余弦函数和函数的简图;
理解的物理意义,掌握由函数的图象到函数的图象的变换原理;
掌握正弦、余弦、正切函数图象的对称轴或对称中心.
教学重点:函数的图象到函数的图象的变换方法.
一、知识点归纳:
“五点法”画正弦、余弦函数和函数的简图.
函数的图象到函数的图象的两种主要途径.
掌握正弦、余弦、正切函数图象的对称轴或对称中心.
会由三角函数图象求出相应的解析式.
二、知识点解析:
“五点法”画正弦、余弦函数和函数的简图,五个特殊点通常都是取三个平衡点,一个最高、一个最低点;
给出图象求的解析式的难点在于的确定,本质为待定系数法,基本方法是:①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到的,通常可由平衡点或最值点确定周期,进而确定.
对称性:函数对称轴可由解出;对称
中心的横坐标是方程的解,对称中心的纵坐标为.( 即整体代换法)
函数对称轴可由解出;对称中心的纵坐标是方程的解,对称中心的横坐标为.( 即整体代换法)
函数对称中心的横坐标可由解出,对称中心的纵坐标为,函数不具有轴对称性.
时,,当时,有最大值,
当时,有最小值;时,与上述情况相反.
(三)典例分析:
问题1. 已知函数.
用“五点法”画出它的图象;求它的振幅、周期和初相;
说明该函数的图象可由的图象经过怎样的变换而得到.
问题2. (
)(海南)函数在区的简图是
(天津文)函数
的部分图象如图所示,则函数表达式为
已知函数()
的一段图象如下图所示,求该函数的解析式.
问题3.将函数的周期扩大到原来的倍,再将函数图象左移,得到图象对应解析式是
(山东文)要得到函数的图象,只需将函数
的图象 向右平移个单位;向右平移个单位;
向左平移个单位;向左平移个单位
(山东)为了得到函数的图象,可以将函数的图象
向右平移个单位长度 向右平移个单位长度
向左平移个单位长度 向左平移个单位长度
问题4.(福建)已知函数的最小正周期为,则
该函数的图象 关于点对称 关于直线对称
关于点对称 .关于直线对称
(山东)已知函数,则下列判断正确的是
此函数的最小正周期为,其图象的一个对称中心是
此函数的最小正周期为,其图象的一个对称中心是
此函数的最小正周期为,其图象的一个对称中心是
此函数的最小正周期为,其图象的一个对称中心是
问题5.(陕西)设函数,其中向量,,,且的图象经过点.(Ⅰ)求实数的值;(Ⅱ)求函数的最小值及此时值的集合.
(四)课外作业:
要得到的图象,只需将的图象
向左平移 向右平移 向左平移 向右平移
如果函数的图象关于直线对称,则
(五)走向高考:
(天津)要得到函数的图象,只需将函数的
图象上所有的点的
横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度
横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度
横坐标伸长到原来的倍(纵坐标不变),再向左平行移动个单位长度
横坐标伸长到原来的倍(纵坐标不变),再向右平行移动个单位长度
(江苏)为了得到函数的图像,只需把函数的图像上所有的点
向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
向右平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
向左平移个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变)
向右平移个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变)
(安徽)函数的图象为,
①图象关于直线对称;②函数在区间内是增函数;
③由的图象向右平移个单位长度可以得到图象.
以上三个论断中,正确论断的个数是
(安徽)将函数的图象按向量
平移,平移后的图象如图所示,
则平移后的图象所对应函数的解析式是
(福建)函数,
)的部分图象如图,则
(福建)已知函数的最小正周期为,则该函数的图象
关于点对称关于直线对称关于点对称关于直线对称
(广东文)已知简谐运动的图象经过点,则该简谐运动的最小正周期和初相分别为
,;,;,;,
(陕西)已知函数
(Ⅰ)求函数的最小正周期;(Ⅱ)求使函数取得最大值的集合.
(全国Ⅰ文)设函数图像的一条对称轴是直线.(Ⅰ)求;(Ⅱ)求函数的单调增区间;
(Ⅲ)画出函数在区间上的图像。
(全国)已知函数是上的偶函数,其图象关于点对称,且在区间上是单调函数。求的值。
三角函数的图象和性质(二)
教学目标:掌握三角函数的定义域、值域的求法;理解周期函数与最小正周期的意义,会求经过简单的恒等变形可化为或的三角函数的周期.
教学重点:求三角函数的定义域是研究其它一切性质的前提.
(一)知识点归纳:
三角函数的定义域、值域及周期如下表:
函数 定义域 值域 周期
(二)知识点解析:
求三角函数的定义域实质就是解三角不等式(组).一般可用三角函数的图象或三角函数线确定三角不等式的解.列三角不等式,既要考虑分式的分母不能为零;偶次方根被开方数大于等于零;对数的真数大于零及底数大于零且不等于1,又要考虑三角函数本身的定义域;
求三角函数的值域的常用方法:①化为求代数函数的值域;②化为求的值域;③化为关于(或)的二次函数式;
三角函数的周期问题一般将函数式化为(其中为三角函数,).
(三)典例分析:
问题1. 求下列函数的定义域:
; ;
问题2.求下列函数的值域:
;;;.
问题3.求下列函数的周期:
;;
问题4.已知函数的定义域为,值域为,求常数的值.
(四)课后作业:
求函数的定义域.
函数的定义域为
若方程有解,则
(江西)设函数,则为( )
周期函数,最小正周期为 周期函数,最小正周期为
周期函数,数小正周期为 非周期函数
(全国Ⅱ)函数的最小正周期是 2
函数的最小正周期为
函数的周期是
已知函数,求的定义域,判断它的奇偶性,并求其值域
(五)走向高考:
(四川)函数的最小正周期为
(上海)函数的最小正周期
(福建)已知函数在区间上的最小值是,则
的最小值等于
(安徽文)解不等式.
(天津)已知函数,.
(Ⅰ)求函数的最小正周期;
(Ⅱ)求函数在区间上的最小值和最大值.
(重庆)设.(Ⅰ)求的最大值及最小正周期;
(Ⅱ)若锐角满足,求的值.
8 / 8
