七年级数学5.3.1 平行线的性质(2)
文档属性
| 名称 | 七年级数学5.3.1 平行线的性质(2) |  | |
| 格式 | zip | ||
| 文件大小 | 275.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-20 11:56:58 | ||
图片预览



文档简介
(共14张PPT)
第五章 相交线与平行线
5.3.1 平行线的性质(2)
5.3 平行线的性质
重庆市开县西街中学 罗堂喜
⑴平行线的判定方法有哪些?
⑵平行线的性质有哪些?
复习回顾
平行线的判定方法 平行线的性质
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
⑶平行线的性质和判定有什么区别?
判定:角的关系 → 平行关系
性质:平行关系 → 角的关系
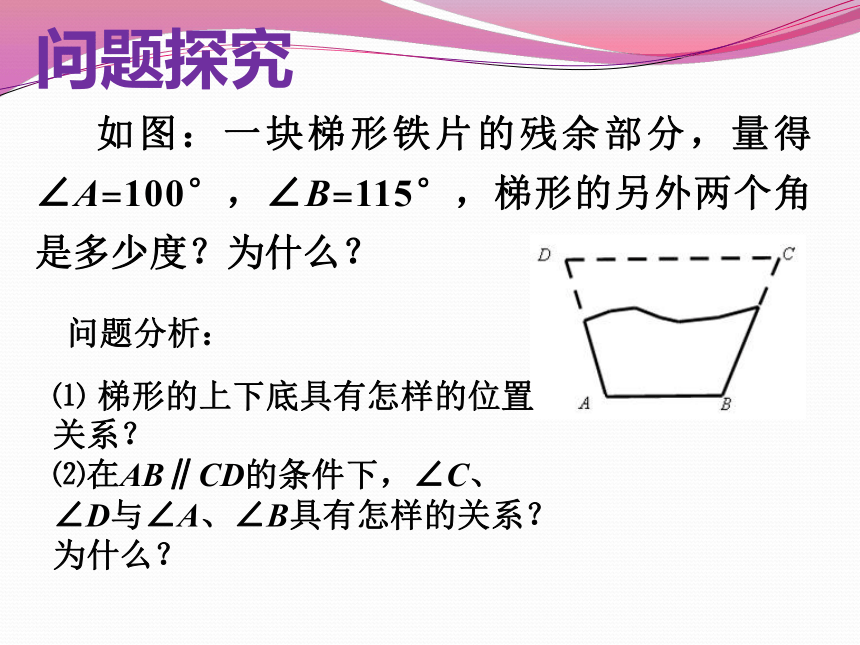
如图:一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角是多少度?为什么?
问题探究
⑴ 梯形的上下底具有怎样的位置关系?
⑵在AB∥CD的条件下,∠C、∠D与∠A、∠B具有怎样的关系?
为什么?
问题分析:
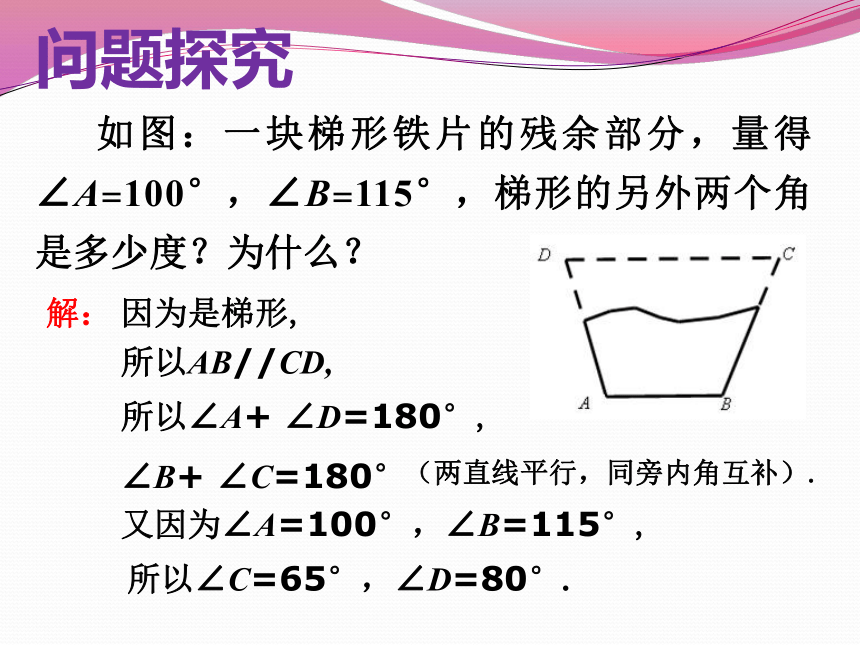
如图:一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角是多少度?为什么?
问题探究
解:
因为是梯形,
所以AB//CD,
所以∠A+ ∠D=180°,
∠B+ ∠C=180°
(两直线平行,同旁内角互补).
又因为∠A=100°,∠B=115°,
所以∠C=65°,∠D=80°.
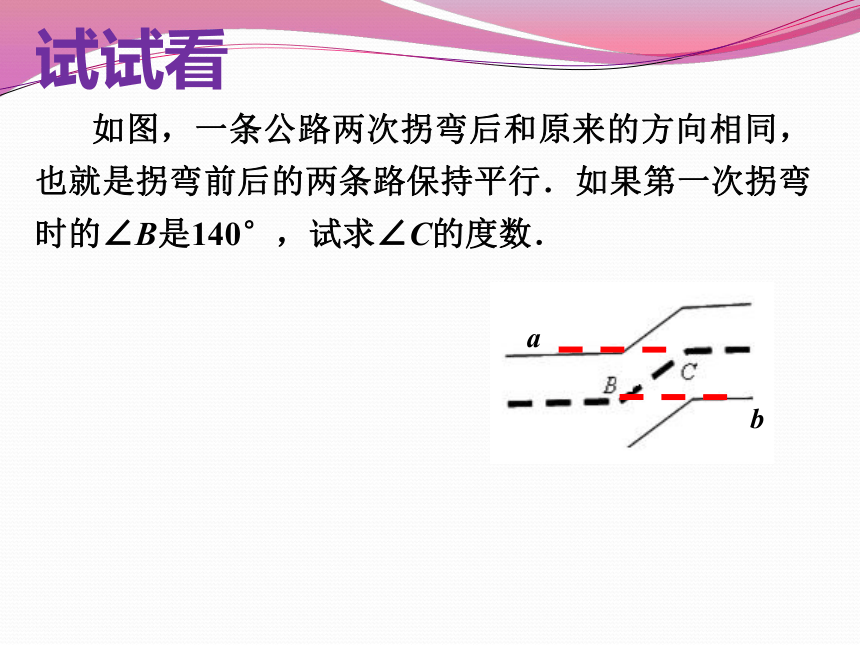
如图,一条公路两次拐弯后和原来的方向相同,也就是拐弯前后的两条路保持平行.如果第一次拐弯时的∠B是140°,试求∠C的度数.
试试看
a
b
如图,∠BHE与∠BGF互为补角,∠D=∠A.求证:∠B=∠C.
综合应用
⑴观察图形中的∠B与∠C具有怎样的位置关系?
⑵AB与CD具有怎样的位置关系时,才能说明∠B=∠C?
⑶由已知条件能说明AB与CD平行吗?
问题分析:
如图,∠BHE与∠BGF互为补角,∠D=∠A.求证:∠B=∠C.
综合应用
解:
因为∠BHE+ ∠BGF=180°,
所以∠BGF= ∠BHA(同角的补角相等),
所以AE//DF(同位角相等,两直线平行),
∠BHE+ ∠BHA=180°,
所以∠A= ∠BFD(两直线平行,同位角相等).
又因为∠D=∠A,所以∠BFD= ∠D,
所以AB//CD(内错角相等,两直线平行).
所以∠B=∠C(两直线平行,内错角相等).
如图所示,是汽车灯的灯碗的纵切面,从位于O点的灯泡发出的两束光线OB和OC经过灯碗反射后,沿BA和CD方向平行射出,如果 ∠ABO=46°,∠DCO=48°,求 ∠BOC.
综合应用
思路点拨:
构造BA和CD的平行线 OE,从而构造出平行线间夹的两对内错角.
E
O
C
B
D
A
如图,已知:AB∥CD。
求证:∠BED=∠B+∠D。
A
B
C
D
E
变式题:1、把题中“折线”(折一次)改为折2次,能得到什么结论
2、若是3次,…N次,又能得到什么结论
总结归纳
求角的大小或者是证明两个角相等、互补的方法之一是利用平行线的性质.当平行线间夹的角不能直接求解时,添加适当的平行线,将要求的角转化为两个平行线间所夹的内错角、同位角或者同旁内角来解答.为了解决问题,自己添加的线叫做辅助线,用虚线表示.
练习巩固
教材P22习题5.3第1题,P23的习题5.3第5、6、7题 .
自我完善
谈一谈本节课你有什么收获?
还有什么疑惑?
作业布置
教科书:第24页第8、10、12题,
第25页第13题.
第五章 相交线与平行线
5.3.1 平行线的性质(2)
5.3 平行线的性质
重庆市开县西街中学 罗堂喜
⑴平行线的判定方法有哪些?
⑵平行线的性质有哪些?
复习回顾
平行线的判定方法 平行线的性质
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
⑶平行线的性质和判定有什么区别?
判定:角的关系 → 平行关系
性质:平行关系 → 角的关系
如图:一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角是多少度?为什么?
问题探究
⑴ 梯形的上下底具有怎样的位置关系?
⑵在AB∥CD的条件下,∠C、∠D与∠A、∠B具有怎样的关系?
为什么?
问题分析:
如图:一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角是多少度?为什么?
问题探究
解:
因为是梯形,
所以AB//CD,
所以∠A+ ∠D=180°,
∠B+ ∠C=180°
(两直线平行,同旁内角互补).
又因为∠A=100°,∠B=115°,
所以∠C=65°,∠D=80°.
如图,一条公路两次拐弯后和原来的方向相同,也就是拐弯前后的两条路保持平行.如果第一次拐弯时的∠B是140°,试求∠C的度数.
试试看
a
b
如图,∠BHE与∠BGF互为补角,∠D=∠A.求证:∠B=∠C.
综合应用
⑴观察图形中的∠B与∠C具有怎样的位置关系?
⑵AB与CD具有怎样的位置关系时,才能说明∠B=∠C?
⑶由已知条件能说明AB与CD平行吗?
问题分析:
如图,∠BHE与∠BGF互为补角,∠D=∠A.求证:∠B=∠C.
综合应用
解:
因为∠BHE+ ∠BGF=180°,
所以∠BGF= ∠BHA(同角的补角相等),
所以AE//DF(同位角相等,两直线平行),
∠BHE+ ∠BHA=180°,
所以∠A= ∠BFD(两直线平行,同位角相等).
又因为∠D=∠A,所以∠BFD= ∠D,
所以AB//CD(内错角相等,两直线平行).
所以∠B=∠C(两直线平行,内错角相等).
如图所示,是汽车灯的灯碗的纵切面,从位于O点的灯泡发出的两束光线OB和OC经过灯碗反射后,沿BA和CD方向平行射出,如果 ∠ABO=46°,∠DCO=48°,求 ∠BOC.
综合应用
思路点拨:
构造BA和CD的平行线 OE,从而构造出平行线间夹的两对内错角.
E
O
C
B
D
A
如图,已知:AB∥CD。
求证:∠BED=∠B+∠D。
A
B
C
D
E
变式题:1、把题中“折线”(折一次)改为折2次,能得到什么结论
2、若是3次,…N次,又能得到什么结论
总结归纳
求角的大小或者是证明两个角相等、互补的方法之一是利用平行线的性质.当平行线间夹的角不能直接求解时,添加适当的平行线,将要求的角转化为两个平行线间所夹的内错角、同位角或者同旁内角来解答.为了解决问题,自己添加的线叫做辅助线,用虚线表示.
练习巩固
教材P22习题5.3第1题,P23的习题5.3第5、6、7题 .
自我完善
谈一谈本节课你有什么收获?
还有什么疑惑?
作业布置
教科书:第24页第8、10、12题,
第25页第13题.
