2020-2021学年八年级数学人教版下册《第18章平行四边形》章末综合复习提升训练(word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册《第18章平行四边形》章末综合复习提升训练(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 393.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览



文档简介
2021年度人教版八年级数学下册《第18章平行四边形》章末综合复习提升训练(附答案)
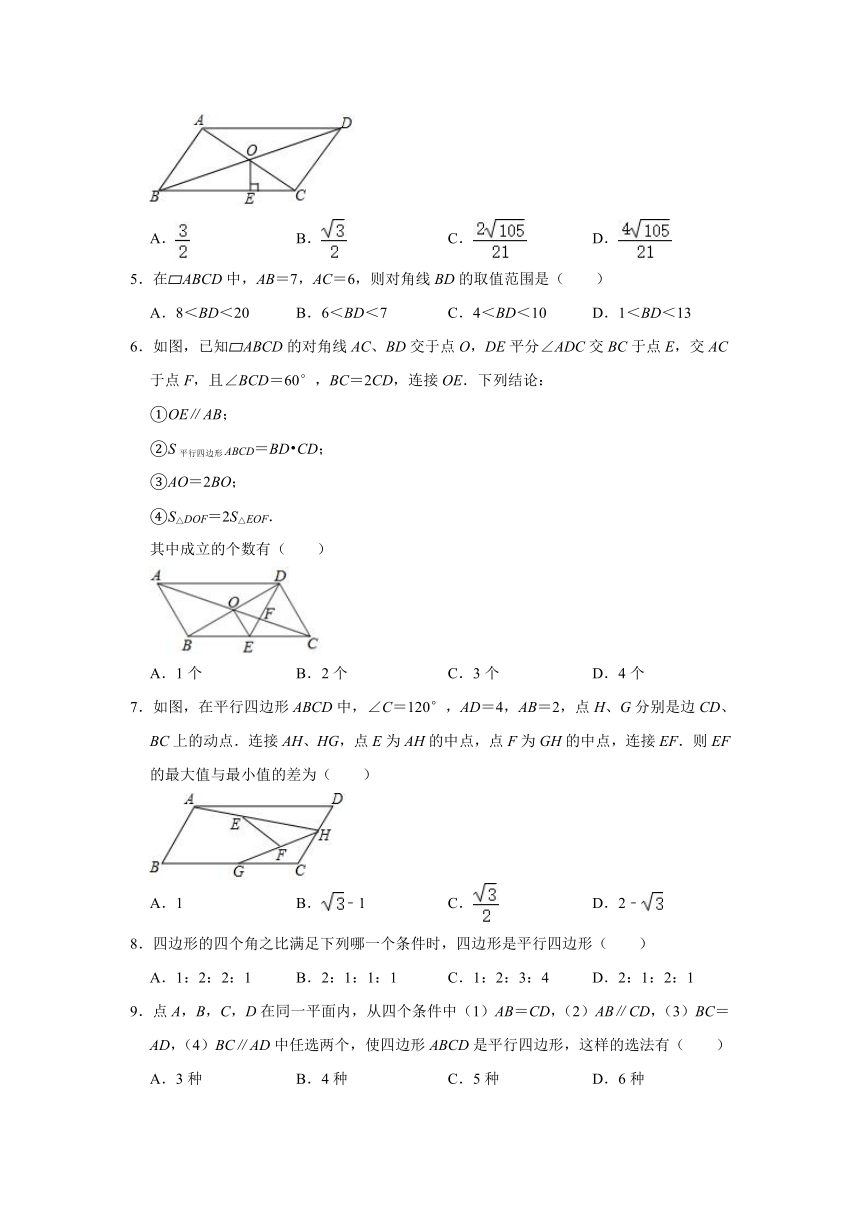
1.如图,在Rt△ABC中,∠B=90°,BC=3,AB=4,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为( )
A.4
B.5
C.5.5
D.6
2.如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为( )
A.10°
B.15°
C.25°
D.40°
3.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )
A.(﹣,)
B.(﹣,)
C.(﹣,)
D.(﹣,)
4.如图,?ABCD的对角线AC与BD相交于点O,OE⊥BC,垂足为E,AB=,AC=4,BD=6,则OE的长为( )
A.
B.
C.
D.
5.在?ABCD中,AB=7,AC=6,则对角线BD的取值范围是( )
A.8<BD<20
B.6<BD<7
C.4<BD<10
D.1<BD<13
6.如图,已知?ABCD的对角线AC、BD交于点O,DE平分∠ADC交BC于点E,交AC于点F,且∠BCD=60°,BC=2CD,连接OE.下列结论:
①OE∥AB;
②S平行四边形ABCD=BD?CD;
③AO=2BO;
④S△DOF=2S△EOF.
其中成立的个数有( )
A.1个
B.2个
C.3个
D.4个
7.如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )
A.1
B.﹣1
C.
D.2﹣
8.四边形的四个角之比满足下列哪一个条件时,四边形是平行四边形( )
A.1:2:2:1
B.2:1:1:1
C.1:2:3:4
D.2:1:2:1
9.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种
B.4种
C.5种
D.6种
10.如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
A.30°
B.40°
C.50°
D.60°
11.如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1
B.
C.
D.
12.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
A.3
B.3
C.2
D.4
13.如图,在?ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )
A.AM=AN
B.MN⊥AC
C.MN是∠AMC的平分线
D.∠BAD=120°
14.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( )
A.AB=AD
B.AC=BD
C.AD=BC
D.AB=CD
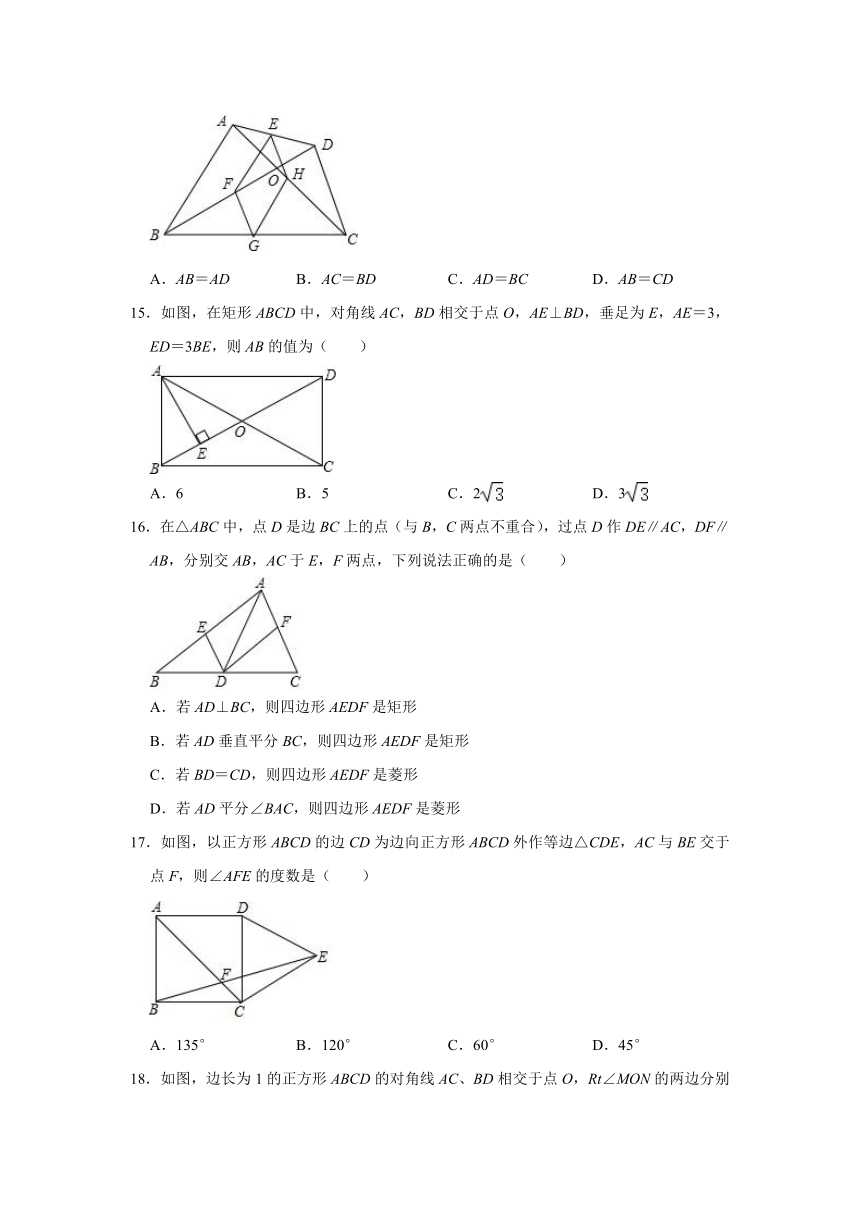
15.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )
A.6
B.5
C.2
D.3
16.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
17.如图,以正方形ABCD的边CD为边向正方形ABCD外作等边△CDE,AC与BE交于点F,则∠AFE的度数是( )
A.135°
B.120°
C.60°
D.45°
18.如图,边长为1的正方形ABCD的对角线AC、BD相交于点O,Rt∠MON的两边分别交边AB、BC于E、F两点,EF交OB于点G,则下列结论中错误的是( )
A.EF=OE
B.四边形OEBF的面积:正方形ABCD的面积=1:4
C.BE+BF=OA
D.当AE=时,△BEF的面积最大
19.四边形ABCD的对角线AC、BD交于点O,有以下结论:①AB=BC;②∠DAB=90°;③BO=DO,AO=CO;④四边形ABCD是矩形;⑤四边形ABCD是菱形;⑥四边形ABCD是正方形.下列推论不正确的是( )
A.由②③,得④
B.由①③,得⑤
C.由①②,得⑥
D.由①④,得⑥
二.填空题(共9小题)
20.如图,在?ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为
cm2.
21.如图,四边形ABCD中,AD∥BC,AD=8cm,BC=12cm,M是BC上一点,且BM=9cm,点E从点A出发以1cm/s的速度向点D运动,点F从点C出发,以3cm/s的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为t,则当以A、M、E、F为顶点的四边形是平行四边形时,t=
22.已知在直角坐标系中有A、B、C、D四个点,其中A,B,C三个点的坐标分别为(0,2),(﹣1,0),(2,0),则当点D的坐标为
时,以A、B、C、D四个点为顶点的四边形是平行四边形.
23.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=2,则CE的长为
24.如图,矩形ABCD中,AB=6,AD=8,P是BC上的点,PE⊥BD于E,PF⊥AC于F,则PF+PE=
.
25.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D是斜边AB上任意一点,DE⊥AC,DF⊥BC,垂足分别是点E、F,点Q是EF的中点,则线段DQ长的最小值等于
.
26.如图,点O是正方形ABCD对角线AC和BD的交点,E是BD上一点,过点D作DF⊥CE于F,交OC于G,过点E作EH⊥BC于H,已知正方形ABCD的边长为2,∠ECH=30°,则线段CG的长为
.
27.如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA.下列四种说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形.
其中,正确的有
(只填写序号)
28.如图,两张宽度均为3cm的纸条交错叠放在一起,相交成锐角α,且两张纸片中重叠部分的面积为9cm2,则锐角α的度数
.
三.解答题(共4小题)
29.如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.
(1)求∠FGH度数;
(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.
30.已知:如图,在?ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求四边形DEBF的周长和面积.
31.如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
32.如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
(1)当H(﹣2,6)时,求证:四边形EFGH是正方形;
(2)若F(﹣5,0),求点G的坐标.
参考答案
1.解:∵∠B=90°,BC=3,AB=4,
∴AC==5,
∵D,E分别是AB,AC的中点,
∴DE=BC=,EC=AC=,DE∥BC,
∴∠FCM=∠EFC,
∵CF平分Rt△ABC的一个外角∠ACM,
∴∠FCM=∠FCE,
∴∠EFC=∠FCE,
∴EF=EC=,
∴DF=DE+EF=4,
故选:A.
2.解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AB,PN=DC,PM∥AB,PN∥DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵∠MPN=130°,
∴∠PMN==25°.
故选:C.
3.解:由题意:第1个三角形的直角顶点坐标:(﹣2,2);
第2个三角形的直角顶点坐标:(﹣1,1);
第3个三角形的第1个三角形的直角顶点坐标:(﹣,);
第4个三角形的直角顶点坐标:(﹣,);
第5个三角形的直角顶点坐标:(﹣,);
第6个三角形的直角顶点坐标:(﹣,);
故选:A.
4.解:如图,过A作AF⊥BC于F.
∵AC=4,BD=6,四边形ABCD是平行四边形,
∴AO=AC=2,BO=BD=3,
∵AB=,
∴AB2+AO2=BO2,
∴∠BAC=90°,
在Rt△BAC中,BC==.
∵S?ABCD=AB×AC=BC×AF,
∴×4=AF,
∴AF=,
∵OE⊥BC,AF⊥BC,
∴OE∥AF,
∴OE=AF=.
故选:C.
5.解:∵四边形ABCD是平行四边形,AB=7,AC=6,
∴OA=OC=AC=3,
在△AOB中,
∵AB﹣OA<OB<AB+OA,
∴4<OB<10,
∵BD=2OB,
∴BD的取值范围是8<BD<20.
故选:A.
6.解:①∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠ADC+∠BCD=180°,
∵∠BCD=60°,
∴∠ADC=120°,
∵DE平分∠ADC,
∴∠CDE=60°=∠BCD,
∴△CDE是等边三角形,
∴CE=CD,
∵BC=2CD,
∴BE=CE,
∵OA=OC,
∴OE∥AB;
故①正确;
②∵△DEC是等边三角形,
∴∠DEC=60°=∠DBC+∠BDE,
∵BE=EC=DE,
∴∠DBC=∠BDE=30°,
∴∠BDC=30°+60°=90°,
∴BD⊥CD,
∴S平行四边形ABCD=BD?CD;
故②正确;
③设AB=x,则AD=2x,则BD=x,
∴OB=,
由勾股定理得:AO==x,
故③不正确;
④∵AD∥EC,
∴DF=2EF,
∴S△DOF=2S△EOF.
故④正确;
故选:C.
7.解:如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.
∵四边形ABCD是平行四边形,∠BCD=120°,
∴∠D=180°﹣∠BCD=60°,AB=CD=2,
∵AM=DM=DC=2,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,CM=DM=AM,
∴∠MAC=∠MCA=30°,
∴∠ACD=90°,
∴AC=2,
在Rt△ACN中,∵AC=2,∠ACN=∠DAC=30°,
∴AN=AC=,
∵AE=EH,GF=FH,
∴EF=AG,
易知AG的最大值为AC的长,最小值为AN的长,
∴AG的最大值为2,最小值为,
∴EF的最大值为,最小值为,
∴EF的最大值与最小值的差为.
故选:C.
8.解:
平行四边形的判定定理之一是:两组对角分别相等的四边形是平行四边形,
即当∠A=∠C,∠B=∠D时,四边形ABCD是平行四边形,
A、∵∠A:∠B:∠C:∠D=1:2:2:1,
∴∠A≠∠C,∠B≠∠D,
∴四边形ABCD不是平行四边形,故本选项错误;
B、∵∠A:∠B:∠C:∠D=2:1:1:1,
∴∠A≠∠C,∠B=∠D,
∴四边形ABCD不是平行四边形,故本选项错误;
C、∵∠A:∠B:∠C:∠D=1:2:3:4,
∴∠A≠∠C,∠B≠∠D,
∴四边形ABCD不是平行四边形,故本选项错误;
D、∵∠A:∠B:∠C:∠D=2:1:2:1,
∴∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,故本选项正确;
故选:D.
9.解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
10.解:∵在△ABC中,∠ACB=90°,E是AB的中点,
∴BE=CE,
∵∠B=20°
∴∠ECB=∠B=20°,
∵AD=BD,∠B=20°,
∴∠DAB=∠B=20°,
∴∠ADC=∠B+∠DAB=20°+20°=40°,
∴∠DFE=∠ADC+∠ECB=40°+20°=60°,
故选:D.
11.解:连接DB,作DH⊥AB于H,如图,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,
而∠A=60°,
∴△ABD和△BCD都是等边三角形,
∴∠ADB=∠DBC=60°,AD=BD,
在Rt△ADH中,AH=1,AD=2,
∴DH=,
在△ADE和△BDF中
,
∴△ADE≌△BDF,
∴∠2=∠1,DE=DF
∴∠1+∠BDE=∠2+∠BDE=∠ADB=60°,
∴△DEF为等边三角形,
∴EF=DE,
而当E点运动到H点时,DE的值最小,其最小值为,
∴EF的最小值为.
故选:D.
12.解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∵四边形ABCD是菱形,
∴BD⊥AC于O,AO=AC=×6=3,
由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=3.
故选:A.
13.解:如图,∵四边形ABCD是平行四边形,
∴∠B=∠D,∠DAB=∠DCB,AB=CD,AD=BC,
∵AM,CN分别是∠BAD和∠BCD的平分线,
∴∠DCN=∠DCB,∠BAM=∠BAD,
∴∠BAM=∠DCN,
在△ABM和△CDN中
,
∴△ABM≌△CDN(ASA),
∴AM=CN,BM=DN,
∵AD=BC,
∴AN=CM,
∴四边形AMCN是平行四边形,
A、∵四边形AMCN是平行四边形,AM=AN,
∴平行四边形AMCN是菱形,故本选项错误;
B、∵MN⊥AC,四边形AMCN是平行四边形,
∴平行四边形AMCN是菱形,故本选项错误;
C、∵四边形AMCN是平行四边形,
∴AN∥BC,
∴∠MNA=∠CMN,
∵MN是∠AMC的平分线,
∴∠NMA=∠NMC,
∴∠MNA=∠NMA,
∴AM=AN,
∵四边形AMCN是平行四边形,
∴四边形AMCN是菱形,故本选项错误;
D、根据∠BAD=120°和平行四边形AMCN不能推出四边形是菱形,故本选项正确;
故选:D.
14.解:∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,
∴EF=GH=AB,EH=FG=CD,
∵当EF=FG=GH=EH时,四边形EFGH是菱形,
∴当AB=CD时,四边形EFGH是菱形.
故选:D.
15.解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠ABD=60°,
∵AE⊥BD,AE=3,
∴AB=2,
故选:C.
16.解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A错误;
若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;
若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;
若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.
17.解:∵四边形ABCD是正方形.
∴AB=AD,∠BAF=∠DAF.
∴△ABF与△ADF全等.
∴∠AFD=∠AFB.
∵CB=CE,∴∠CBE=∠CEB.
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,
∴∠CBE=15°.
∵∠ACB=45°,
∴∠AFB=∠ACB+∠CBE=60°.
∴∠AFE=120°.
故选:B.
18.解:∵正方形ABCD对角线交于O点
∴OB=OC,∠EBO=FCO=45°,∠BOC=90°
∵∠MON=90°
∴∠EOB=∠FOC
∴△EOB≌△FOC(ASA)
∴OE=OF,BE=FC,△EOB与△FOC面积相等;
∴△EOF为等腰直角三角形,选项A可证;
∴S四边形OEBF=S△OEB+S△BOF=S△BOC选项B可证;
∴BE+BF=FC+BF=BC≠OA,选项C排除;
设BE=x,则S△BEF=x(1﹣x)=
所以,当x=时,S△BEF最大,选项D可证;
故选:C.
19.解:只有C选项符合题意,选项A、B、D都不符合题意,
理由是:四边形ABCD中,AB=BC,∠DAB=90°,无法得到四边形ABCD是正方形.
故选:C.
20.解:连接E、F两点,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=16cm2,S△BQC=25cm2,
∴S四边形EPFQ=41cm2,
故答案为:41.
21.解:①当点F在线段BM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=9+3t﹣12,解得t=,
②当F在线段CM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=12﹣9﹣3t,解得t=,
综上所述,t=或s时,以A、M、E、F为顶点的四边形是平行四边形.
故答案为:或
22.解:如图所示:
故答案为:(3,2)、(﹣3,2)、(1,﹣2).
23.解:∵四边形ABCD是菱形,
∴AB=AD=6,AC⊥BD,OB=OD,OA=OC,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=6,
∴OB=BD=3,
∴OC=OA=,
∴AC=2OA=6,
∵点E在AC上,OE=2,
∴当E在点O左边时CE=OC+2=5,
当点E在点O右边时CE=OC﹣2=,
∴CE=5或;
故答案为:5或.
24.解:连接OP,
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB?BC=12,OA=OC,OB=OD,AC=BD,AC==10,
∴S△BOC=S矩形ABCD=×6×8=12,OB=OC=AC=5,
∴S△BOC=S△OBP+S△OCP=OB?PE+OC?PF=OB(PE+PF)=12,
∴PE+PF=.
故答案为:.
25.解:∵在△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=10,
连接CD,
∵DE⊥AC,DF⊥BC,
∴四边形EDFC是矩形,
∴EF=CD,∠EDF=90°,
∵点Q是EF的中点,
∴DQ=EF=CD,
当CD最小时,则DQ最小,
根据垂线段最短可知当CD⊥AB时,则CD最小,
∴DQ=EF=CD=×=2.4,
故答案为:2.4.
26.解:四边形ABCD是正方形,
∴AC⊥BD,OD=OC,
∴∠DOG=∠COE=90°,
∴∠OEC+∠OCE=90°,
∵DF⊥CE,
∴∠OEC+∠ODG=90°,
∴∠ODG=∠OCE,
在△DOG和△COE中
∴△DOG≌△COE(ASA),
∴OE=OG,
∵四边形ABCD是正方形,
∴OB=OC,
∴CG=BE,
∵四边形BACD是正方形,
∴∠OBC=45°,
∵EH⊥BC,
∴∠BHE=∠CHE=90°,
∴BH=HE,
设BH=HE=x,
∵∠ECH=30°,
∴CH=EH=x,
∵BC=2,
∴x+x=2
解得:x=﹣1,
即BH=EH=﹣1,
在Rt△BHE中,由勾股定理得:BE==﹣,
∴CG=BE=﹣,
故答案为:﹣.
27.解:∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形,故①正确;
∵四边形AEDF是平行四边形,∠BAC=90°,
∴四边形AEDF是矩形,故②正确;
∵AD平分∠BAC,四边形AEDF是平行四边形,
∴四边形AEDF是菱形,故③正确;
∵若AD平分∠BAC,则平行四边形AEDF是菱形,
∴若∠BAC=90°,则平行四边形AEDF是正方形,故④正确.
故答案为:①②③④.
28.解:过点D作DE⊥BC于E,过点B作BF⊥CD于F,
∴∠DEC=∠BFC=90°,
∵两张宽度均为3cm的纸条交错叠放在一起,
∴AD∥BC,AB∥CD,BF=DE=3,
∴四边形ABCD是平行四边形,
∵∠DCE=∠BCF,
∴△DEC≌△BFC(AAS),
∴BC=DC,
∴四边形ABCD是菱形,
∵两张纸片中重叠部分的面积为9cm2,
∴BC?DE=9,
∴BC=CD=3(cm),
∵∠DCE=∠α,
∴∠α=45°.
故答案为:45°.
29.解:(1)∵F、G、H分别是DE、BE、BC的中点,
∴FG∥DB,GH∥EC.
∴∠DBE=∠FGE,∠EGH=∠AEG.
∠FGH=∠FGE+∠EGH=∠ABE+∠BEA=180°﹣∠A=180°﹣90°=90°.
(2)如图所示:连接FM、HM.
∵M、H分别是BC和DC的中点,
∴MH∥BD,MH=.
同理:GF∥BD,GF=.
∴四边形FGHM为平行四边形.
∵G、H、M分别是BE、BC、DC的中点,
∴GH==3,,
由(1)可知:∠FGH=90°,
∴四边形FGHM为矩形.
∴∠GHM=90°.
∴GM==5.
30.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB﹣AE=CD﹣CF
即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形.
∴BD、EF互相平分;
(2)∵∠A=60°,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,
∵AE=2EB,
∴BE=2,
∴四边形DEBF的周长=2(BE+DE)=2(4+2)=12,
过D点作DG⊥AB于点G,
在Rt△ADG中,AD=4,∠A=60°,
∴DG=2,
∴四边形DEBF的面积=BE×DG=2×2=4.
31.(1)证明:∵AE⊥CE于E,AF⊥CF于F,
∴∠AEC=∠AFC=90°,
又∵CE、CF分别平分∠ACB与它的邻补角∠ACD,
∴∠BCE=∠ACE,∠ACF=∠DCF,
∴∠ACE+∠ACF=(∠BCE+∠ACE+∠ACF+∠DCF)=×180°=90°,
∴三个角为直角的四边形AECF为矩形.
(2)结论:MN∥BC且MN=BC.
证明:∵四边形AECF为矩形,
∴对角线相等且互相平分,
∴NE=NC,
∴∠NEC=∠ACE=∠BCE,
∴MN∥BC,
又∵AN=CN(矩形的对角线相等且互相平分),
∴N是AC的中点,
若M不是AB的中点,则可在AB取中点M1,连接M1N,
则M1N是△ABC的中位线,MN∥BC,
而MN∥BC,M1即为点M,
所以MN是△ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)
∴MN=BC;
法二:延长MN至K,使NK=MN,
因为对角线互相平分,
所以AMCK是平行四边形,KC∥MA,KC=AM因为MN∥BC,
所以MBCK是平行四边形,MK=BC,
所以MN=BC
(3)解:△ABC是直角三角形(∠ACB=90°).
理由:∵四边形AECF是菱形,
∴AC⊥EF,
∵EF∥AC,
∴AC⊥CB,
∴∠ACB=90°.即△ABC是直角三角形.
32.解:(1)∵四边形ABCD是正方形,
∴∠BAO=∠AOC=90°,
∵E(0,2),H(﹣2,6),
∴AH=OE=2,
∵四边形EFGH是菱形,
∴EH=EF,
在Rt△AHE和Rt△OEF中,
,
∴Rt△AHE≌Rt△OEF,
∴∠AEH=∠EFO,
∵∠EFO+∠FEO=90°,
∴∠AEH+∠FEO=90°,
∴∠HEF=90°,∵四边形EFGH是菱形,
∴四边形EFGH是正方形.
(2)连接EG交FH于K.
∵HE=EF,
∴AH2+AE2=EO2+OF2,
∴AH2+16=4+25,
∴AH=,
∴H(﹣,6),
∵KH=KF,
∴K(﹣,3),
∵GK=KE,
∴G(﹣5﹣,4).
1.如图,在Rt△ABC中,∠B=90°,BC=3,AB=4,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为( )
A.4
B.5
C.5.5
D.6
2.如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为( )
A.10°
B.15°
C.25°
D.40°
3.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )
A.(﹣,)
B.(﹣,)
C.(﹣,)
D.(﹣,)
4.如图,?ABCD的对角线AC与BD相交于点O,OE⊥BC,垂足为E,AB=,AC=4,BD=6,则OE的长为( )
A.
B.
C.
D.
5.在?ABCD中,AB=7,AC=6,则对角线BD的取值范围是( )
A.8<BD<20
B.6<BD<7
C.4<BD<10
D.1<BD<13
6.如图,已知?ABCD的对角线AC、BD交于点O,DE平分∠ADC交BC于点E,交AC于点F,且∠BCD=60°,BC=2CD,连接OE.下列结论:
①OE∥AB;
②S平行四边形ABCD=BD?CD;
③AO=2BO;
④S△DOF=2S△EOF.
其中成立的个数有( )
A.1个
B.2个
C.3个
D.4个
7.如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )
A.1
B.﹣1
C.
D.2﹣
8.四边形的四个角之比满足下列哪一个条件时,四边形是平行四边形( )
A.1:2:2:1
B.2:1:1:1
C.1:2:3:4
D.2:1:2:1
9.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种
B.4种
C.5种
D.6种
10.如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
A.30°
B.40°
C.50°
D.60°
11.如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1
B.
C.
D.
12.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
A.3
B.3
C.2
D.4
13.如图,在?ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )
A.AM=AN
B.MN⊥AC
C.MN是∠AMC的平分线
D.∠BAD=120°
14.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( )
A.AB=AD
B.AC=BD
C.AD=BC
D.AB=CD
15.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )
A.6
B.5
C.2
D.3
16.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
17.如图,以正方形ABCD的边CD为边向正方形ABCD外作等边△CDE,AC与BE交于点F,则∠AFE的度数是( )
A.135°
B.120°
C.60°
D.45°
18.如图,边长为1的正方形ABCD的对角线AC、BD相交于点O,Rt∠MON的两边分别交边AB、BC于E、F两点,EF交OB于点G,则下列结论中错误的是( )
A.EF=OE
B.四边形OEBF的面积:正方形ABCD的面积=1:4
C.BE+BF=OA
D.当AE=时,△BEF的面积最大
19.四边形ABCD的对角线AC、BD交于点O,有以下结论:①AB=BC;②∠DAB=90°;③BO=DO,AO=CO;④四边形ABCD是矩形;⑤四边形ABCD是菱形;⑥四边形ABCD是正方形.下列推论不正确的是( )
A.由②③,得④
B.由①③,得⑤
C.由①②,得⑥
D.由①④,得⑥
二.填空题(共9小题)
20.如图,在?ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为
cm2.
21.如图,四边形ABCD中,AD∥BC,AD=8cm,BC=12cm,M是BC上一点,且BM=9cm,点E从点A出发以1cm/s的速度向点D运动,点F从点C出发,以3cm/s的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为t,则当以A、M、E、F为顶点的四边形是平行四边形时,t=
22.已知在直角坐标系中有A、B、C、D四个点,其中A,B,C三个点的坐标分别为(0,2),(﹣1,0),(2,0),则当点D的坐标为
时,以A、B、C、D四个点为顶点的四边形是平行四边形.
23.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=2,则CE的长为
24.如图,矩形ABCD中,AB=6,AD=8,P是BC上的点,PE⊥BD于E,PF⊥AC于F,则PF+PE=
.
25.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D是斜边AB上任意一点,DE⊥AC,DF⊥BC,垂足分别是点E、F,点Q是EF的中点,则线段DQ长的最小值等于
.
26.如图,点O是正方形ABCD对角线AC和BD的交点,E是BD上一点,过点D作DF⊥CE于F,交OC于G,过点E作EH⊥BC于H,已知正方形ABCD的边长为2,∠ECH=30°,则线段CG的长为
.
27.如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA.下列四种说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形.
其中,正确的有
(只填写序号)
28.如图,两张宽度均为3cm的纸条交错叠放在一起,相交成锐角α,且两张纸片中重叠部分的面积为9cm2,则锐角α的度数
.
三.解答题(共4小题)
29.如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.
(1)求∠FGH度数;
(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.
30.已知:如图,在?ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求四边形DEBF的周长和面积.
31.如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
32.如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
(1)当H(﹣2,6)时,求证:四边形EFGH是正方形;
(2)若F(﹣5,0),求点G的坐标.
参考答案
1.解:∵∠B=90°,BC=3,AB=4,
∴AC==5,
∵D,E分别是AB,AC的中点,
∴DE=BC=,EC=AC=,DE∥BC,
∴∠FCM=∠EFC,
∵CF平分Rt△ABC的一个外角∠ACM,
∴∠FCM=∠FCE,
∴∠EFC=∠FCE,
∴EF=EC=,
∴DF=DE+EF=4,
故选:A.
2.解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AB,PN=DC,PM∥AB,PN∥DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵∠MPN=130°,
∴∠PMN==25°.
故选:C.
3.解:由题意:第1个三角形的直角顶点坐标:(﹣2,2);
第2个三角形的直角顶点坐标:(﹣1,1);
第3个三角形的第1个三角形的直角顶点坐标:(﹣,);
第4个三角形的直角顶点坐标:(﹣,);
第5个三角形的直角顶点坐标:(﹣,);
第6个三角形的直角顶点坐标:(﹣,);
故选:A.
4.解:如图,过A作AF⊥BC于F.
∵AC=4,BD=6,四边形ABCD是平行四边形,
∴AO=AC=2,BO=BD=3,
∵AB=,
∴AB2+AO2=BO2,
∴∠BAC=90°,
在Rt△BAC中,BC==.
∵S?ABCD=AB×AC=BC×AF,
∴×4=AF,
∴AF=,
∵OE⊥BC,AF⊥BC,
∴OE∥AF,
∴OE=AF=.
故选:C.
5.解:∵四边形ABCD是平行四边形,AB=7,AC=6,
∴OA=OC=AC=3,
在△AOB中,
∵AB﹣OA<OB<AB+OA,
∴4<OB<10,
∵BD=2OB,
∴BD的取值范围是8<BD<20.
故选:A.
6.解:①∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠ADC+∠BCD=180°,
∵∠BCD=60°,
∴∠ADC=120°,
∵DE平分∠ADC,
∴∠CDE=60°=∠BCD,
∴△CDE是等边三角形,
∴CE=CD,
∵BC=2CD,
∴BE=CE,
∵OA=OC,
∴OE∥AB;
故①正确;
②∵△DEC是等边三角形,
∴∠DEC=60°=∠DBC+∠BDE,
∵BE=EC=DE,
∴∠DBC=∠BDE=30°,
∴∠BDC=30°+60°=90°,
∴BD⊥CD,
∴S平行四边形ABCD=BD?CD;
故②正确;
③设AB=x,则AD=2x,则BD=x,
∴OB=,
由勾股定理得:AO==x,
故③不正确;
④∵AD∥EC,
∴DF=2EF,
∴S△DOF=2S△EOF.
故④正确;
故选:C.
7.解:如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.
∵四边形ABCD是平行四边形,∠BCD=120°,
∴∠D=180°﹣∠BCD=60°,AB=CD=2,
∵AM=DM=DC=2,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,CM=DM=AM,
∴∠MAC=∠MCA=30°,
∴∠ACD=90°,
∴AC=2,
在Rt△ACN中,∵AC=2,∠ACN=∠DAC=30°,
∴AN=AC=,
∵AE=EH,GF=FH,
∴EF=AG,
易知AG的最大值为AC的长,最小值为AN的长,
∴AG的最大值为2,最小值为,
∴EF的最大值为,最小值为,
∴EF的最大值与最小值的差为.
故选:C.
8.解:
平行四边形的判定定理之一是:两组对角分别相等的四边形是平行四边形,
即当∠A=∠C,∠B=∠D时,四边形ABCD是平行四边形,
A、∵∠A:∠B:∠C:∠D=1:2:2:1,
∴∠A≠∠C,∠B≠∠D,
∴四边形ABCD不是平行四边形,故本选项错误;
B、∵∠A:∠B:∠C:∠D=2:1:1:1,
∴∠A≠∠C,∠B=∠D,
∴四边形ABCD不是平行四边形,故本选项错误;
C、∵∠A:∠B:∠C:∠D=1:2:3:4,
∴∠A≠∠C,∠B≠∠D,
∴四边形ABCD不是平行四边形,故本选项错误;
D、∵∠A:∠B:∠C:∠D=2:1:2:1,
∴∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,故本选项正确;
故选:D.
9.解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
10.解:∵在△ABC中,∠ACB=90°,E是AB的中点,
∴BE=CE,
∵∠B=20°
∴∠ECB=∠B=20°,
∵AD=BD,∠B=20°,
∴∠DAB=∠B=20°,
∴∠ADC=∠B+∠DAB=20°+20°=40°,
∴∠DFE=∠ADC+∠ECB=40°+20°=60°,
故选:D.
11.解:连接DB,作DH⊥AB于H,如图,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,
而∠A=60°,
∴△ABD和△BCD都是等边三角形,
∴∠ADB=∠DBC=60°,AD=BD,
在Rt△ADH中,AH=1,AD=2,
∴DH=,
在△ADE和△BDF中
,
∴△ADE≌△BDF,
∴∠2=∠1,DE=DF
∴∠1+∠BDE=∠2+∠BDE=∠ADB=60°,
∴△DEF为等边三角形,
∴EF=DE,
而当E点运动到H点时,DE的值最小,其最小值为,
∴EF的最小值为.
故选:D.
12.解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∵四边形ABCD是菱形,
∴BD⊥AC于O,AO=AC=×6=3,
由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=3.
故选:A.
13.解:如图,∵四边形ABCD是平行四边形,
∴∠B=∠D,∠DAB=∠DCB,AB=CD,AD=BC,
∵AM,CN分别是∠BAD和∠BCD的平分线,
∴∠DCN=∠DCB,∠BAM=∠BAD,
∴∠BAM=∠DCN,
在△ABM和△CDN中
,
∴△ABM≌△CDN(ASA),
∴AM=CN,BM=DN,
∵AD=BC,
∴AN=CM,
∴四边形AMCN是平行四边形,
A、∵四边形AMCN是平行四边形,AM=AN,
∴平行四边形AMCN是菱形,故本选项错误;
B、∵MN⊥AC,四边形AMCN是平行四边形,
∴平行四边形AMCN是菱形,故本选项错误;
C、∵四边形AMCN是平行四边形,
∴AN∥BC,
∴∠MNA=∠CMN,
∵MN是∠AMC的平分线,
∴∠NMA=∠NMC,
∴∠MNA=∠NMA,
∴AM=AN,
∵四边形AMCN是平行四边形,
∴四边形AMCN是菱形,故本选项错误;
D、根据∠BAD=120°和平行四边形AMCN不能推出四边形是菱形,故本选项正确;
故选:D.
14.解:∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,
∴EF=GH=AB,EH=FG=CD,
∵当EF=FG=GH=EH时,四边形EFGH是菱形,
∴当AB=CD时,四边形EFGH是菱形.
故选:D.
15.解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠ABD=60°,
∵AE⊥BD,AE=3,
∴AB=2,
故选:C.
16.解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A错误;
若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;
若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;
若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.
17.解:∵四边形ABCD是正方形.
∴AB=AD,∠BAF=∠DAF.
∴△ABF与△ADF全等.
∴∠AFD=∠AFB.
∵CB=CE,∴∠CBE=∠CEB.
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,
∴∠CBE=15°.
∵∠ACB=45°,
∴∠AFB=∠ACB+∠CBE=60°.
∴∠AFE=120°.
故选:B.
18.解:∵正方形ABCD对角线交于O点
∴OB=OC,∠EBO=FCO=45°,∠BOC=90°
∵∠MON=90°
∴∠EOB=∠FOC
∴△EOB≌△FOC(ASA)
∴OE=OF,BE=FC,△EOB与△FOC面积相等;
∴△EOF为等腰直角三角形,选项A可证;
∴S四边形OEBF=S△OEB+S△BOF=S△BOC选项B可证;
∴BE+BF=FC+BF=BC≠OA,选项C排除;
设BE=x,则S△BEF=x(1﹣x)=
所以,当x=时,S△BEF最大,选项D可证;
故选:C.
19.解:只有C选项符合题意,选项A、B、D都不符合题意,
理由是:四边形ABCD中,AB=BC,∠DAB=90°,无法得到四边形ABCD是正方形.
故选:C.
20.解:连接E、F两点,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=16cm2,S△BQC=25cm2,
∴S四边形EPFQ=41cm2,
故答案为:41.
21.解:①当点F在线段BM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=9+3t﹣12,解得t=,
②当F在线段CM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=12﹣9﹣3t,解得t=,
综上所述,t=或s时,以A、M、E、F为顶点的四边形是平行四边形.
故答案为:或
22.解:如图所示:
故答案为:(3,2)、(﹣3,2)、(1,﹣2).
23.解:∵四边形ABCD是菱形,
∴AB=AD=6,AC⊥BD,OB=OD,OA=OC,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=6,
∴OB=BD=3,
∴OC=OA=,
∴AC=2OA=6,
∵点E在AC上,OE=2,
∴当E在点O左边时CE=OC+2=5,
当点E在点O右边时CE=OC﹣2=,
∴CE=5或;
故答案为:5或.
24.解:连接OP,
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB?BC=12,OA=OC,OB=OD,AC=BD,AC==10,
∴S△BOC=S矩形ABCD=×6×8=12,OB=OC=AC=5,
∴S△BOC=S△OBP+S△OCP=OB?PE+OC?PF=OB(PE+PF)=12,
∴PE+PF=.
故答案为:.
25.解:∵在△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=10,
连接CD,
∵DE⊥AC,DF⊥BC,
∴四边形EDFC是矩形,
∴EF=CD,∠EDF=90°,
∵点Q是EF的中点,
∴DQ=EF=CD,
当CD最小时,则DQ最小,
根据垂线段最短可知当CD⊥AB时,则CD最小,
∴DQ=EF=CD=×=2.4,
故答案为:2.4.
26.解:四边形ABCD是正方形,
∴AC⊥BD,OD=OC,
∴∠DOG=∠COE=90°,
∴∠OEC+∠OCE=90°,
∵DF⊥CE,
∴∠OEC+∠ODG=90°,
∴∠ODG=∠OCE,
在△DOG和△COE中
∴△DOG≌△COE(ASA),
∴OE=OG,
∵四边形ABCD是正方形,
∴OB=OC,
∴CG=BE,
∵四边形BACD是正方形,
∴∠OBC=45°,
∵EH⊥BC,
∴∠BHE=∠CHE=90°,
∴BH=HE,
设BH=HE=x,
∵∠ECH=30°,
∴CH=EH=x,
∵BC=2,
∴x+x=2
解得:x=﹣1,
即BH=EH=﹣1,
在Rt△BHE中,由勾股定理得:BE==﹣,
∴CG=BE=﹣,
故答案为:﹣.
27.解:∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形,故①正确;
∵四边形AEDF是平行四边形,∠BAC=90°,
∴四边形AEDF是矩形,故②正确;
∵AD平分∠BAC,四边形AEDF是平行四边形,
∴四边形AEDF是菱形,故③正确;
∵若AD平分∠BAC,则平行四边形AEDF是菱形,
∴若∠BAC=90°,则平行四边形AEDF是正方形,故④正确.
故答案为:①②③④.
28.解:过点D作DE⊥BC于E,过点B作BF⊥CD于F,
∴∠DEC=∠BFC=90°,
∵两张宽度均为3cm的纸条交错叠放在一起,
∴AD∥BC,AB∥CD,BF=DE=3,
∴四边形ABCD是平行四边形,
∵∠DCE=∠BCF,
∴△DEC≌△BFC(AAS),
∴BC=DC,
∴四边形ABCD是菱形,
∵两张纸片中重叠部分的面积为9cm2,
∴BC?DE=9,
∴BC=CD=3(cm),
∵∠DCE=∠α,
∴∠α=45°.
故答案为:45°.
29.解:(1)∵F、G、H分别是DE、BE、BC的中点,
∴FG∥DB,GH∥EC.
∴∠DBE=∠FGE,∠EGH=∠AEG.
∠FGH=∠FGE+∠EGH=∠ABE+∠BEA=180°﹣∠A=180°﹣90°=90°.
(2)如图所示:连接FM、HM.
∵M、H分别是BC和DC的中点,
∴MH∥BD,MH=.
同理:GF∥BD,GF=.
∴四边形FGHM为平行四边形.
∵G、H、M分别是BE、BC、DC的中点,
∴GH==3,,
由(1)可知:∠FGH=90°,
∴四边形FGHM为矩形.
∴∠GHM=90°.
∴GM==5.
30.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB﹣AE=CD﹣CF
即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形.
∴BD、EF互相平分;
(2)∵∠A=60°,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,
∵AE=2EB,
∴BE=2,
∴四边形DEBF的周长=2(BE+DE)=2(4+2)=12,
过D点作DG⊥AB于点G,
在Rt△ADG中,AD=4,∠A=60°,
∴DG=2,
∴四边形DEBF的面积=BE×DG=2×2=4.
31.(1)证明:∵AE⊥CE于E,AF⊥CF于F,
∴∠AEC=∠AFC=90°,
又∵CE、CF分别平分∠ACB与它的邻补角∠ACD,
∴∠BCE=∠ACE,∠ACF=∠DCF,
∴∠ACE+∠ACF=(∠BCE+∠ACE+∠ACF+∠DCF)=×180°=90°,
∴三个角为直角的四边形AECF为矩形.
(2)结论:MN∥BC且MN=BC.
证明:∵四边形AECF为矩形,
∴对角线相等且互相平分,
∴NE=NC,
∴∠NEC=∠ACE=∠BCE,
∴MN∥BC,
又∵AN=CN(矩形的对角线相等且互相平分),
∴N是AC的中点,
若M不是AB的中点,则可在AB取中点M1,连接M1N,
则M1N是△ABC的中位线,MN∥BC,
而MN∥BC,M1即为点M,
所以MN是△ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)
∴MN=BC;
法二:延长MN至K,使NK=MN,
因为对角线互相平分,
所以AMCK是平行四边形,KC∥MA,KC=AM因为MN∥BC,
所以MBCK是平行四边形,MK=BC,
所以MN=BC
(3)解:△ABC是直角三角形(∠ACB=90°).
理由:∵四边形AECF是菱形,
∴AC⊥EF,
∵EF∥AC,
∴AC⊥CB,
∴∠ACB=90°.即△ABC是直角三角形.
32.解:(1)∵四边形ABCD是正方形,
∴∠BAO=∠AOC=90°,
∵E(0,2),H(﹣2,6),
∴AH=OE=2,
∵四边形EFGH是菱形,
∴EH=EF,
在Rt△AHE和Rt△OEF中,
,
∴Rt△AHE≌Rt△OEF,
∴∠AEH=∠EFO,
∵∠EFO+∠FEO=90°,
∴∠AEH+∠FEO=90°,
∴∠HEF=90°,∵四边形EFGH是菱形,
∴四边形EFGH是正方形.
(2)连接EG交FH于K.
∵HE=EF,
∴AH2+AE2=EO2+OF2,
∴AH2+16=4+25,
∴AH=,
∴H(﹣,6),
∵KH=KF,
∴K(﹣,3),
∵GK=KE,
∴G(﹣5﹣,4).
