2020-2021学年沪科版八年级数学下册18章勾股定理专题试卷(word版含答案)
文档属性
| 名称 | 2020-2021学年沪科版八年级数学下册18章勾股定理专题试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 408.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览

文档简介
第18章
勾股定理专题
1.【解答题】如图,在四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB上一点,AE=4,ED=5,求CD的长.
2.【解答题】(2019·呼和浩特改编)如图,在△ABC中,内角∠A,∠B,∠C所对应的边分别为a,b,c.若a,b,c满足=,求证:△ABC是直角三角形.
3.【解答题】已知△ABC的三边a=m-n(m>n>0),b=m+n,c=2.
(1)求证:△ABC是直角三角形;
(2)利用(1)的结论,写出两组m,n的值,要求三角形的边长均为整数.
4.【解答题】(2020·芜湖无为县期末)在一条东西走向的河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=BC,由于某种原因,由C到B的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点D(A,D,B在同一条直线上),并新修一条路CD,测得CA=6.5千米,CD=6千米,AD=2.5千米.
(1)问CD是否为从村庄C到河边最近的路?请通过计算加以说明;
(2)求原来的路线BC的长.
5.【解答题】(2019·安徽T23变式)如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,CD=PC=2,CD⊥CP,求∠BPC的度数.
6.【解答题】(2019·合肥瑶海区二模)法国数学家费尔马早在17世纪就研究过形如x2+y2=z2的方程,显然,这个方程有无数组解.我们把满足该方程的正整数的解(x,y,z)叫做勾股数.如(3,4,5)就是一组勾股数.
(1)请你再写出两组勾股数:(_____),(_____);
(2)在研究直角三角形的勾股数时,古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2-1,z=n2+1,那么以x,y,z为三边的三角形为直角三角形(即x,y,z为勾股数),请你加以证明.
7.【解答题】(2020·安庆期末)如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点都在格点上.
(1)求四边形ABCD的周长;
(2)连接AC,试判断△ACD的形状,并说明理由.
8.【解答题】(2019·阜阳期中)如图,在8×8的正方形网格中,每个小正方形的边长为1
cm.
(1)在正方形方格网中画出△ABC,使AB=
cm,AC=2
cm,BC=5
cm;
(2)计算△ABC的面积.
9.【解答题】如图,在Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使点C与AB的中点D重合,折痕交AC于点M,交BC于点N.
(1)求线段BN的长;
(2)连接CD,与MN交于点E,写出与点E相关的两个正确结论:①_____;②_____.
10.【解答题】(2019·马鞍山二模)若正整数a,b,c(a第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25);…
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
11.【解答题】根据三角形的三边a,b,c的长,判断△ABC是不是直角三角形:
(1)a=61,b=60,c=11;
(2)a=,b=1,c=.
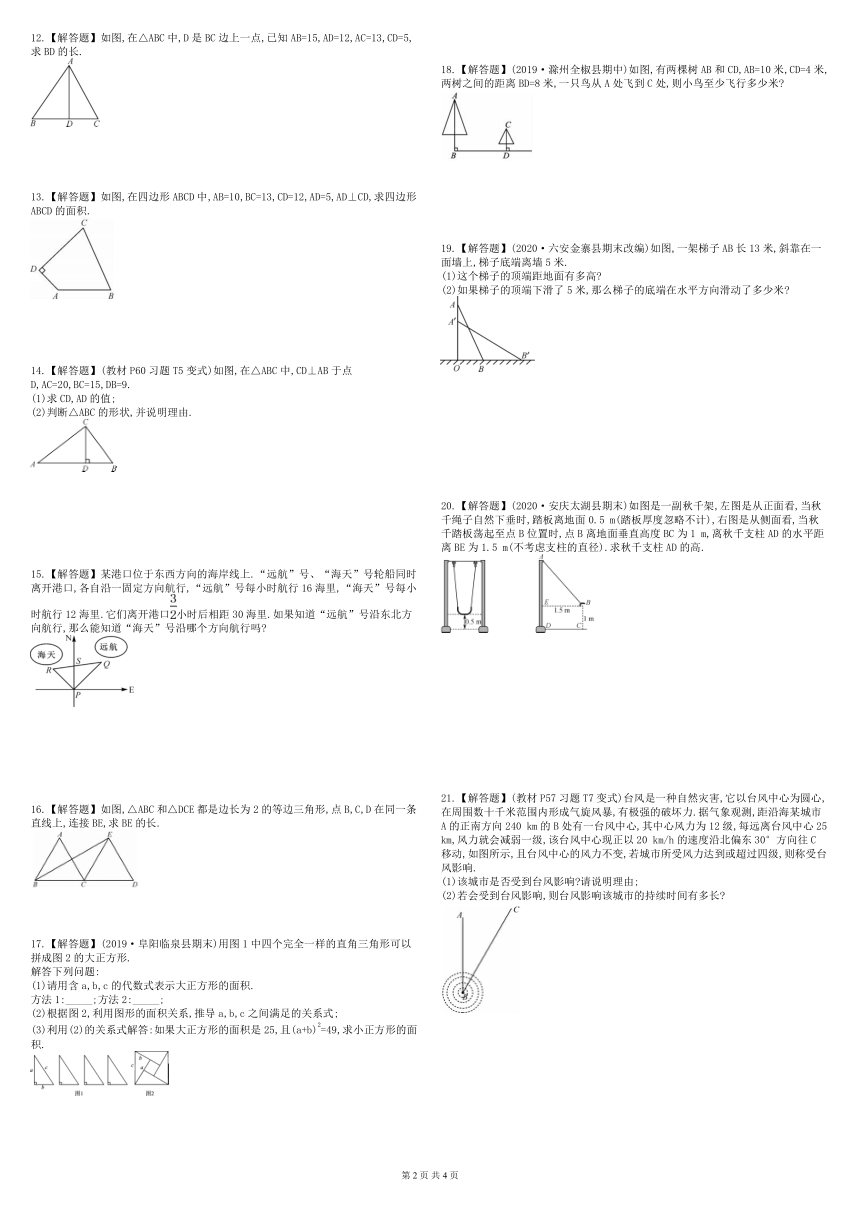
12.【解答题】如图,在△ABC中,D是BC边上一点,已知AB=15,AD=12,AC=13,CD=5,求BD的长.
13.【解答题】如图,在四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
14.【解答题】(教材P60习题T5变式)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9.
(1)求CD,AD的值;
(2)判断△ABC的形状,并说明理由.
15.【解答题】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口小时后相距30海里.如果知道“远航”号沿东北方向航行,那么能知道“海天”号沿哪个方向航行吗?
16.【解答题】如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,D在同一条直线上,连接BE,求BE的长.
17.【解答题】(2019·阜阳临泉县期末)用图1中四个完全一样的直角三角形可以拼成图2的大正方形.
解答下列问题:
(1)请用含a,b,c的代数式表示大正方形的面积.
方法1:_____;方法2:_____;
(2)根据图2,利用图形的面积关系,推导a,b,c之间满足的关系式;
(3)利用(2)的关系式解答:如果大正方形的面积是25,且(a+b)2=49,求小正方形的面积.
18.【解答题】(2019·滁州全椒县期中)如图,有两棵树AB和CD,AB=10米,CD=4米,两树之间的距离BD=8米,一只鸟从A处飞到C处,则小鸟至少飞行多少米?
19.【解答题】(2020·六安金寨县期末改编)如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?
20.【解答题】(2020·安庆太湖县期末)如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5
m(踏板厚度忽略不计),右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1
m,离秋千支柱AD的水平距离BE为1.5
m(不考虑支柱的直径).求秋千支柱AD的高.
21.【解答题】(教材P57习题T7变式)台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.据气象观测,距沿海某城市A的正南方向240
km的B处有一台风中心,其中心风力为12级,每远离台风中心25
km,风力就会减弱一级,该台风中心现正以20
km/h的速度沿北偏东30°方向往C移动,如图所示,且台风中心的风力不变,若城市所受风力达到或超过四级,则称受台风影响.
(1)该城市是否受到台风影响?请说明理由;
(2)若会受到台风影响,则台风影响该城市的持续时间有多长?
【参考答案】
1.解:∵AD=3,AE=4,ED=5,
∴AD2+AE2=ED2.
∴∠A=90°.
∴DA⊥AB.
∵∠C=90°,BD平分∠ABC,
∴DC=AD.
∵AD=3,
∴CD=3.
2.证明:原式可变形为=,
∴(a+c)2-b2=2ac,即a2+2ac+c2-b2=2ac.
∴a2+c2=b2.
∴△ABC是以∠B为直角的直角三角形.
3.解:(1)证明:∵a=m-n(m>n>0),b=m+n,c=2,
∴a2+c2=(m-n)2+(2)2=m2+n2-2mn+4mn=(m+n)2.
∴a2+c2=b2.
∴△ABC是直角三角形.
(2)当m=4,n=1时,三角形的边长为3,4,5;
当m=9,n=4时,三角形的边长为5,12,13.
4.解:(1)是,理由:
∵62+2.52=6.52,
∴CD2+AD2=AC2.
∴△ADC为直角三角形.
∴CD⊥AB.
∴CD是从村庄C到河边最近的路.
(2)设AB=BC=x千米,则BD=(x-2.5)千米,
∵CD⊥AB,则在Rt△BDC中,CD2+BD2=BC2.
∴62+(x-2.5)2=x2.
解得x=8.45.
答:原来的路线BC的长为8.45千米.
5.解:连接BD.
∵CD⊥CP,CP=CD=2,
∴△CPD为等腰直角三角形.
∴∠CPD=45°.
∵∠ACP+∠BCP=∠BCP+∠BCD=90°,
∴∠ACP=∠BCD.
∵CA=CB,
∴△CAP≌△CBD(SAS).
∴DB=PA=3.
在Rt△CPD中,DP2=CP2+CD2=22+22=8.
又∵PB=1,DB2=9,
∴DB2=DP2+PB2=8+1=9.
∴∠DPB=90°.
∴∠CPB=∠CPD+∠DPB=45°+90°=135°.
6.解:(1)(6,8,10);(9,12,15)
(2)证明:x2+y2=(2n)2+(n2-1)2
=4n2+n4-2n2+1
=n4+2n2+1
=(n2+1)2
=z2,
即x,y,z为勾股数.
7.解:(1)由题意可知AB==3,AD==,DC==2,BC==,
∴四边形ABCD的周长为AB+BC+CD+AD=+3+3.
(2)△ACD是直角三角形.理由如下:
∵AD=,DC=2,AC=5,
∴AD2+CD2=AC2.
∴△ACD是直角三角形.
8.解:(1)如图,△ABC即为所求.
(2)S△ABC=×5×2=5.
9.解:(1)∵D是AB的中点,
∴BD=AB=3.
设BN=x,则CN=9-x.
由翻折的性质可知:
DN=CN=9-x.
在Rt△BDN中,由勾股定理,得
DN2=BD2+NB2,即(9-x)2=32+x2.
解得x=4.
∴BN的长为4.
(2)①DE=EC;②∠DEM=90°
10.解:(1)第一组(a是奇数):9,40,41(答案不唯一);
第二组(a是偶数):12,35,37(答案不唯一).
(2)当a为奇数时,b=,c=;
当a为偶数时,b=-1,c=+1;
证明:当a为奇数时,a2+b2=a2+()2=()2=c2,
∴(a,b,c)是“勾股数”.
当a为偶数时,a2+b2=a2+(-1)2=(+1)2=c2,
∴(a,b,c)是“勾股数”.
11.解:(1)∵最大边是a,且a2=3
721,
b2+c2=602+112=3
721,
∴a2=b2+c2.
∴△ABC是直角三角形(∠A为直角).
(2)∵最大边是c,且c2=,
a2+b2=()2+12=≠,
∴a2+b2≠c2.
∴△ABC不是直角三角形.
12.解:在△ACD中,AD2+CD2=122+52=169,AC2=132=169,
∴AD2+CD2=AC2.
∴△ACD是直角三角形,且∠ADC=90°.
∴∠ADB=90°.
在Rt△ABD中,
BD2=AB2-AD2=152-122=81,
∴BD=9.
13.解:连接AC,过点C作CE⊥AB于点E.
∵AD⊥CD,
∴∠D=90°.
在Rt△ACD中,AD=5,CD=12,
AC===13.
∵BC=13,∴AC=BC.
∵CE⊥AB,AB=10,
∴AE=BE=AB=×10=5.
在Rt△CAE中,
CE===12.
∴S四边形ABCD=S△DAC+S△ABC=×5×12+×10×12=30+60=90.
14.解:(1)∵CD⊥AB,
∴△BCD和△ACD都是直角三角形.
∴CD==12,AD==16.
(2)△ABC为直角三角形,
理由:∵AD=16,BD=9,
∴AB=AD+BD=16+9=25.
∵AC2+BC2=202+152=625=252=AB2,
∴△ABC为直角三角形.
15.解:根据题意,得PQ=16×=24(海里),PR=12×=18(海里),QR=30海里.
∵242+182=302,即PQ2+PR2=QR2.
∴∠QPR=90°.
由“远航”号沿东北方向航行可知,∠QPS=45°,
∴∠SPR=45°,即“海天”号沿西北方向航行.
16.解:过点E作EF⊥BD,垂足为F.
∵△DCE为等边三角形,
∴EF是△DCE的中线.
∴CF=CD=1.
∴BF=BC+CF=2+1=3.
在Rt△EFC中,由勾股定理,得EF2=EC2-CF2=22-12=3.
在Rt△EFB中,由勾股定理,得BE2=BF2+EF2=32+3=12,∴BE=2.
17.解:(1)4×ab+(a-b)2;c2
(2)因为S大正方形=4×ab+(a-b)2=a2+b2,S大正方形=c2,
所以a2+b2=c2.
(3)由(2)知,a2+b2=c2=25.又(a+b)2=49,
所以
2ab=49-(a2+b2)=49-c2=49-25=24.
因为S小正方形=(a-b)2=a2+b2-2ab,
所以小正方形的面积为25-24=1.
18.解:连接AC,作CE⊥AB于点E,
则AE=10-4=6(米),CE=BD=8米.
∴
AC===10(米).
答:小鸟至少飞行10米.
19.解:(1)梯子距离地面的高度AO===12(米).
答:这个梯子的顶端距地面有12米高.
(2)梯子下滑了5米即梯子距离地面的高度OA′=12-5=7(米),
根据勾股定理,得OB′===2(米),
∴BB′=OB′-OB=(2-5)米.
答:当梯子的顶端下滑5米时,梯子的底端在水平方向移动了(2-5)米.
20.解:设AD=x
m,则由题意可得AB=(x-0.5)m,AE=(x-1)m,
在Rt△ABE中,AE2+BE2=AB2.
即(x-1)2+1.52=(x-0.5)2,
解得x=3.
答:秋千支柱AD的高为3
m.
21.解:(1)该城市受到台风的影响.
理由:过点A作AD⊥BC,垂足为D.
在Rt△ADB中,∵∠ABD=30°,
∴AD=AB=×240=120(km).
城市A开始受到台风影响的距离为25×(12-4)=200(km).
∵120<200,
∴该城市受到台风的影响.
(2)设台风中心移至点E处时,该城市开始受到台风的影响,台风中心移至点F处时,该城市脱离台风影响,则AE=AF=200
km.
由勾股定理,得
DE2=AE2-AD2=2002-1202=1602,
∴DE=160
km.
同理,DF=160
km.
∴t===16(h).
答:该城市受台风影响的时间为16
h.
勾股定理专题
1.【解答题】如图,在四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB上一点,AE=4,ED=5,求CD的长.
2.【解答题】(2019·呼和浩特改编)如图,在△ABC中,内角∠A,∠B,∠C所对应的边分别为a,b,c.若a,b,c满足=,求证:△ABC是直角三角形.
3.【解答题】已知△ABC的三边a=m-n(m>n>0),b=m+n,c=2.
(1)求证:△ABC是直角三角形;
(2)利用(1)的结论,写出两组m,n的值,要求三角形的边长均为整数.
4.【解答题】(2020·芜湖无为县期末)在一条东西走向的河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=BC,由于某种原因,由C到B的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点D(A,D,B在同一条直线上),并新修一条路CD,测得CA=6.5千米,CD=6千米,AD=2.5千米.
(1)问CD是否为从村庄C到河边最近的路?请通过计算加以说明;
(2)求原来的路线BC的长.
5.【解答题】(2019·安徽T23变式)如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,CD=PC=2,CD⊥CP,求∠BPC的度数.
6.【解答题】(2019·合肥瑶海区二模)法国数学家费尔马早在17世纪就研究过形如x2+y2=z2的方程,显然,这个方程有无数组解.我们把满足该方程的正整数的解(x,y,z)叫做勾股数.如(3,4,5)就是一组勾股数.
(1)请你再写出两组勾股数:(_____),(_____);
(2)在研究直角三角形的勾股数时,古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2-1,z=n2+1,那么以x,y,z为三边的三角形为直角三角形(即x,y,z为勾股数),请你加以证明.
7.【解答题】(2020·安庆期末)如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点都在格点上.
(1)求四边形ABCD的周长;
(2)连接AC,试判断△ACD的形状,并说明理由.
8.【解答题】(2019·阜阳期中)如图,在8×8的正方形网格中,每个小正方形的边长为1
cm.
(1)在正方形方格网中画出△ABC,使AB=
cm,AC=2
cm,BC=5
cm;
(2)计算△ABC的面积.
9.【解答题】如图,在Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使点C与AB的中点D重合,折痕交AC于点M,交BC于点N.
(1)求线段BN的长;
(2)连接CD,与MN交于点E,写出与点E相关的两个正确结论:①_____;②_____.
10.【解答题】(2019·马鞍山二模)若正整数a,b,c(a
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
11.【解答题】根据三角形的三边a,b,c的长,判断△ABC是不是直角三角形:
(1)a=61,b=60,c=11;
(2)a=,b=1,c=.
12.【解答题】如图,在△ABC中,D是BC边上一点,已知AB=15,AD=12,AC=13,CD=5,求BD的长.
13.【解答题】如图,在四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
14.【解答题】(教材P60习题T5变式)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9.
(1)求CD,AD的值;
(2)判断△ABC的形状,并说明理由.
15.【解答题】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口小时后相距30海里.如果知道“远航”号沿东北方向航行,那么能知道“海天”号沿哪个方向航行吗?
16.【解答题】如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,D在同一条直线上,连接BE,求BE的长.
17.【解答题】(2019·阜阳临泉县期末)用图1中四个完全一样的直角三角形可以拼成图2的大正方形.
解答下列问题:
(1)请用含a,b,c的代数式表示大正方形的面积.
方法1:_____;方法2:_____;
(2)根据图2,利用图形的面积关系,推导a,b,c之间满足的关系式;
(3)利用(2)的关系式解答:如果大正方形的面积是25,且(a+b)2=49,求小正方形的面积.
18.【解答题】(2019·滁州全椒县期中)如图,有两棵树AB和CD,AB=10米,CD=4米,两树之间的距离BD=8米,一只鸟从A处飞到C处,则小鸟至少飞行多少米?
19.【解答题】(2020·六安金寨县期末改编)如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?
20.【解答题】(2020·安庆太湖县期末)如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5
m(踏板厚度忽略不计),右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1
m,离秋千支柱AD的水平距离BE为1.5
m(不考虑支柱的直径).求秋千支柱AD的高.
21.【解答题】(教材P57习题T7变式)台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.据气象观测,距沿海某城市A的正南方向240
km的B处有一台风中心,其中心风力为12级,每远离台风中心25
km,风力就会减弱一级,该台风中心现正以20
km/h的速度沿北偏东30°方向往C移动,如图所示,且台风中心的风力不变,若城市所受风力达到或超过四级,则称受台风影响.
(1)该城市是否受到台风影响?请说明理由;
(2)若会受到台风影响,则台风影响该城市的持续时间有多长?
【参考答案】
1.解:∵AD=3,AE=4,ED=5,
∴AD2+AE2=ED2.
∴∠A=90°.
∴DA⊥AB.
∵∠C=90°,BD平分∠ABC,
∴DC=AD.
∵AD=3,
∴CD=3.
2.证明:原式可变形为=,
∴(a+c)2-b2=2ac,即a2+2ac+c2-b2=2ac.
∴a2+c2=b2.
∴△ABC是以∠B为直角的直角三角形.
3.解:(1)证明:∵a=m-n(m>n>0),b=m+n,c=2,
∴a2+c2=(m-n)2+(2)2=m2+n2-2mn+4mn=(m+n)2.
∴a2+c2=b2.
∴△ABC是直角三角形.
(2)当m=4,n=1时,三角形的边长为3,4,5;
当m=9,n=4时,三角形的边长为5,12,13.
4.解:(1)是,理由:
∵62+2.52=6.52,
∴CD2+AD2=AC2.
∴△ADC为直角三角形.
∴CD⊥AB.
∴CD是从村庄C到河边最近的路.
(2)设AB=BC=x千米,则BD=(x-2.5)千米,
∵CD⊥AB,则在Rt△BDC中,CD2+BD2=BC2.
∴62+(x-2.5)2=x2.
解得x=8.45.
答:原来的路线BC的长为8.45千米.
5.解:连接BD.
∵CD⊥CP,CP=CD=2,
∴△CPD为等腰直角三角形.
∴∠CPD=45°.
∵∠ACP+∠BCP=∠BCP+∠BCD=90°,
∴∠ACP=∠BCD.
∵CA=CB,
∴△CAP≌△CBD(SAS).
∴DB=PA=3.
在Rt△CPD中,DP2=CP2+CD2=22+22=8.
又∵PB=1,DB2=9,
∴DB2=DP2+PB2=8+1=9.
∴∠DPB=90°.
∴∠CPB=∠CPD+∠DPB=45°+90°=135°.
6.解:(1)(6,8,10);(9,12,15)
(2)证明:x2+y2=(2n)2+(n2-1)2
=4n2+n4-2n2+1
=n4+2n2+1
=(n2+1)2
=z2,
即x,y,z为勾股数.
7.解:(1)由题意可知AB==3,AD==,DC==2,BC==,
∴四边形ABCD的周长为AB+BC+CD+AD=+3+3.
(2)△ACD是直角三角形.理由如下:
∵AD=,DC=2,AC=5,
∴AD2+CD2=AC2.
∴△ACD是直角三角形.
8.解:(1)如图,△ABC即为所求.
(2)S△ABC=×5×2=5.
9.解:(1)∵D是AB的中点,
∴BD=AB=3.
设BN=x,则CN=9-x.
由翻折的性质可知:
DN=CN=9-x.
在Rt△BDN中,由勾股定理,得
DN2=BD2+NB2,即(9-x)2=32+x2.
解得x=4.
∴BN的长为4.
(2)①DE=EC;②∠DEM=90°
10.解:(1)第一组(a是奇数):9,40,41(答案不唯一);
第二组(a是偶数):12,35,37(答案不唯一).
(2)当a为奇数时,b=,c=;
当a为偶数时,b=-1,c=+1;
证明:当a为奇数时,a2+b2=a2+()2=()2=c2,
∴(a,b,c)是“勾股数”.
当a为偶数时,a2+b2=a2+(-1)2=(+1)2=c2,
∴(a,b,c)是“勾股数”.
11.解:(1)∵最大边是a,且a2=3
721,
b2+c2=602+112=3
721,
∴a2=b2+c2.
∴△ABC是直角三角形(∠A为直角).
(2)∵最大边是c,且c2=,
a2+b2=()2+12=≠,
∴a2+b2≠c2.
∴△ABC不是直角三角形.
12.解:在△ACD中,AD2+CD2=122+52=169,AC2=132=169,
∴AD2+CD2=AC2.
∴△ACD是直角三角形,且∠ADC=90°.
∴∠ADB=90°.
在Rt△ABD中,
BD2=AB2-AD2=152-122=81,
∴BD=9.
13.解:连接AC,过点C作CE⊥AB于点E.
∵AD⊥CD,
∴∠D=90°.
在Rt△ACD中,AD=5,CD=12,
AC===13.
∵BC=13,∴AC=BC.
∵CE⊥AB,AB=10,
∴AE=BE=AB=×10=5.
在Rt△CAE中,
CE===12.
∴S四边形ABCD=S△DAC+S△ABC=×5×12+×10×12=30+60=90.
14.解:(1)∵CD⊥AB,
∴△BCD和△ACD都是直角三角形.
∴CD==12,AD==16.
(2)△ABC为直角三角形,
理由:∵AD=16,BD=9,
∴AB=AD+BD=16+9=25.
∵AC2+BC2=202+152=625=252=AB2,
∴△ABC为直角三角形.
15.解:根据题意,得PQ=16×=24(海里),PR=12×=18(海里),QR=30海里.
∵242+182=302,即PQ2+PR2=QR2.
∴∠QPR=90°.
由“远航”号沿东北方向航行可知,∠QPS=45°,
∴∠SPR=45°,即“海天”号沿西北方向航行.
16.解:过点E作EF⊥BD,垂足为F.
∵△DCE为等边三角形,
∴EF是△DCE的中线.
∴CF=CD=1.
∴BF=BC+CF=2+1=3.
在Rt△EFC中,由勾股定理,得EF2=EC2-CF2=22-12=3.
在Rt△EFB中,由勾股定理,得BE2=BF2+EF2=32+3=12,∴BE=2.
17.解:(1)4×ab+(a-b)2;c2
(2)因为S大正方形=4×ab+(a-b)2=a2+b2,S大正方形=c2,
所以a2+b2=c2.
(3)由(2)知,a2+b2=c2=25.又(a+b)2=49,
所以
2ab=49-(a2+b2)=49-c2=49-25=24.
因为S小正方形=(a-b)2=a2+b2-2ab,
所以小正方形的面积为25-24=1.
18.解:连接AC,作CE⊥AB于点E,
则AE=10-4=6(米),CE=BD=8米.
∴
AC===10(米).
答:小鸟至少飞行10米.
19.解:(1)梯子距离地面的高度AO===12(米).
答:这个梯子的顶端距地面有12米高.
(2)梯子下滑了5米即梯子距离地面的高度OA′=12-5=7(米),
根据勾股定理,得OB′===2(米),
∴BB′=OB′-OB=(2-5)米.
答:当梯子的顶端下滑5米时,梯子的底端在水平方向移动了(2-5)米.
20.解:设AD=x
m,则由题意可得AB=(x-0.5)m,AE=(x-1)m,
在Rt△ABE中,AE2+BE2=AB2.
即(x-1)2+1.52=(x-0.5)2,
解得x=3.
答:秋千支柱AD的高为3
m.
21.解:(1)该城市受到台风的影响.
理由:过点A作AD⊥BC,垂足为D.
在Rt△ADB中,∵∠ABD=30°,
∴AD=AB=×240=120(km).
城市A开始受到台风影响的距离为25×(12-4)=200(km).
∵120<200,
∴该城市受到台风的影响.
(2)设台风中心移至点E处时,该城市开始受到台风的影响,台风中心移至点F处时,该城市脱离台风影响,则AE=AF=200
km.
由勾股定理,得
DE2=AE2-AD2=2002-1202=1602,
∴DE=160
km.
同理,DF=160
km.
∴t===16(h).
答:该城市受台风影响的时间为16
h.
