2020-2021学年沪科版八年级数学下册第18章 勾股定理单元基础练试题(word版含答案)
文档属性
| 名称 | 2020-2021学年沪科版八年级数学下册第18章 勾股定理单元基础练试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 817.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 11:01:10 | ||
图片预览




文档简介
2020-2021学年沪科版八年级数学下册第18章
勾股定理单元基础练试题
一、单选题
1.下列各组数是勾股数的一组是(
)
A.7,24,25
B.,,
C.1.5,2,2.5
D.32,42,52
2.中,、、的对边分别为、、,若,则有(
)
A.
B.
C.
D.
3.如图,等腰直角三角形ABC中,∠C=90°,腰AC长4,那么点C的坐标是(
)
A.(2,1)
B.(2,2)
C.(2,2)
D.(1,2)
4.如图所示,已知圆柱的底面周长为36,高AB=5,P点位于圆周顶面处,小虫在圆柱侧面爬行,从A点爬到P点,然后再爬回C点,则小虫爬行的最短路程为(
)
A.26
B.13+
C.13
D.2
5.如图,在长方形ABCD中,AB=3,BC=6,对角线AC的垂直平分线分别交AD、AC于点M,N,连接CM,则CM的长为(
)
A.
B.
C.-
D.-
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,则图中所有正方形的面积的和是(
)
A.
B.
C.
D.
7.《九章算术》是我国古代的数学名著,书中有“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部尺远,问折断处离地面的高度是多少?设折断处离地面的高度为尺,则可列方程为(
)
A.
B.
C.
D.
8.四边形中,,则的值为(
)
A.15
B.
C.
D.20
9.如图,中,,,,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则线段的长为(
)
A.
B.
C.
D.
10.如图,P
是等边三角形
ABC
内的一点,且
PA=3,PB=4,PC=5,以
BC
为边在△ABC
外作△BQC≌△BPA,连接
PQ,则以下结论中正确有(
)
①△BPQ
是等边三角形
;
②△PCQ
是直角三角形;③∠APB=150°;④∠APC=120°;
A.①②
B.①③
C.①②③
D.①②④
二、填空题
11.如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=50,点P到AD的距离是30,有一只蚂蚁要从点P爬到点B,则蚂蚁的最短行程为_____.
12.在△ABC中,∠B=30°,AB=8,AC=5,则△ABC的面积为_____.
13.已知直角坐标平面内的点,和,那么的形状是______.
14.如图,点E在正方形ABCD内,AE=6,BE=8,AB=10,则阴影部分的面积为___________.
15.在锐角三角形ABC中,,,BD平分.若M,N分别是边BD,BC上的动点,则的最小值是____.
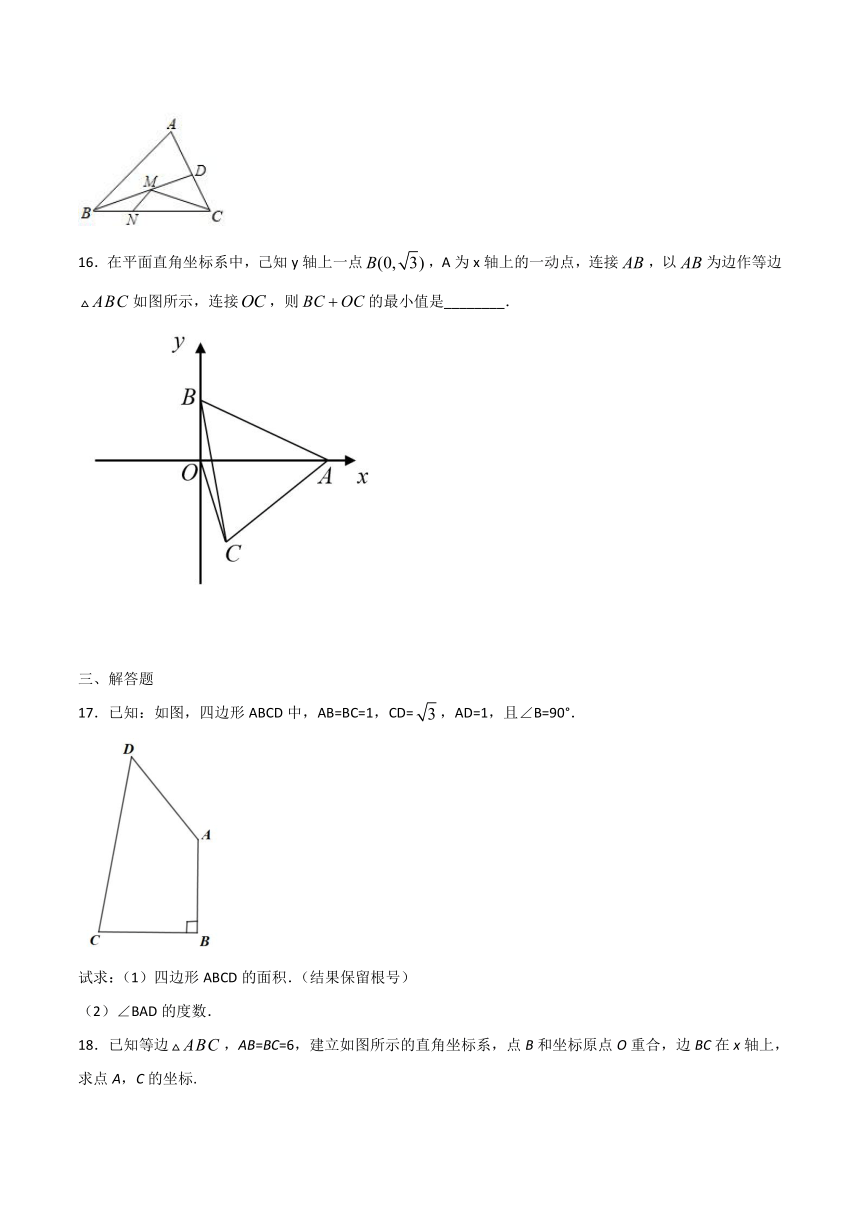
16.在平面直角坐标系中,己知y轴上一点,A为x轴上的一动点,连接,以为边作等边如图所示,连接,则的最小值是________.
三、解答题
17.已知:如图,四边形ABCD中,AB=BC=1,CD=,AD=1,且∠B=90°.
试求:(1)四边形ABCD的面积.(结果保留根号)
(2)∠BAD的度数.
18.已知等边,AB=BC=6,建立如图所示的直角坐标系,点B和坐标原点O重合,边BC在x轴上,求点A,C的坐标.
19.如图,小明家在一条东西走向的公路北侧米的点处,小红家位于小明家北米(米)、东米(米)点处.
(1)求小明家离小红家的距离;
(2)现要在公路上的点处建一个快递驿站,使最小,请确定点的位置,并求的最小值.
20.如图,在中,,,,.
(1)求线段的长;
(2)求的长.
21.如图,长方形纸片,,将长方形纸片折叠,使点D与点B重合,点C落在点处,折痕为,
(1)求证:.
(2)若,求的度数.
(3)若,,求的长.
22.如图1,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于点F,∠ABC=45°,FD=CD.
(1)请写出BE与AC的位置关系,并说明理由;
(2)如图2,连接DE,求证:∠BED=∠DEC;
(3)若AD=4,CD=2,在直线BC上方的平面内是否存在点P,使得△BFP为等腰直角三角形.若存在,请直接写出点P到直线BC的距离.
参考答案
1.A
解:A、72+242=252,三边是整数,同时能构成直角三角形,故是勾股数,此选项符合题意;
B、,不是正整数,不是勾股数,此选项不合题意;
C、1.5,2.5,不是正整数,不是勾股数,此选项不合题意;
D、92+162≠252,不是勾股数,不合题意.
故选:A.
2.A
,
∴是直角三角形,且,
故选:A.
3.C
解:过C作CD⊥AB于D,如图所示:
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB==AC=4,AD=BD=AB=2,
∴CD=AB=AD=2,
∴点C的坐标是(2,2),
4.B
解:如图,
根据题意,AB=CD=5,AC=BD=,
∵P点位于圆周顶面处,
∴DP=BD=6,则BP=BD-DP=12,
∴小虫爬行的最短路程.
故选:B.
5.A
解:∵四边形ABCD是矩形,
∴∠D=∠B=90°,AD=BC=6,AB=DC=3,
∵MN是AC的垂直平分线,
∴AM=CM,
∴DM=AD-AM=AD-CM=6-CM,
在Rt△DMC中,由勾股定理得:DM2+DC2=CM2,
(6-CM)2+32=CM2,
解得:CM=,
6.D
解:如图,设正方形A、B、C、D、E、F的边长分别为a、b、c、d、x、f
所有的三角形都是直角三角形
由勾股定理可得,,
S正方形A+S正方形B=S正方形E,S正方形C+S正方形D=S正方形F,S正方形E+S正方形F=64
S正方形A+S正方形B+
S正方形C+S正方形D+
S正方形E+S正方形F+82
=2(S正方形E+S正方形F)+64
=264+64
=192(cm2)
所有的正方形的面积和是192cm2
7.D
解:设折断处离地面的高度为尺,则斜边为(10-x)尺,
根据勾股定理得:,
8.D
解:如图,把△ABC绕点A逆时针旋转90°得到△ADE,连接CE,作EM⊥CD于M,
则AC=AE=,∠CAE=90°,∠ADE=∠ABC,DE=BC=12,
在Rt△ACE中,CE=,
∵∠BAD=90°,∠BCD=30°,
∴∠ABC+∠ADC=360°-30°-90°=240°,
∴∠ADE+∠ADC=240°,
∴∠CDE=120°,即∠EDM=60°,
∴在Rt△EDM中,∠DEM=30°
∴,
在Rt△CEM中,设CD=x,则CM=6+x
∴,解得:(舍去),
∴CD=20
故选:D
9.A
解:∵Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5,
根据折叠的性质可知AC=CD,∠A=∠CDE,CE⊥AB,
∴B′D=BC﹣CD=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FD=90°,
∵S△ABC=AC?BC=AB?CE,
∴AC?BC=AB?CE,
∴CE=,
∴EF=,ED=AE=,
∴DF=EF﹣ED=
∴B′F=.
选:A.
10.C
解:①∵△ABC是等边三角形,
∴∠ABC=60°,
∵△BQC≌△BPA,
∴∠CBQ=∠ABP,PB=QB=4,
PA=QC=3,∠BPA=∠BQC,
∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,
∴△BPQ是等边三角形,
所以①正确;
②PQ=PB=4,
PQ2+QC2=42+32=25,
PC2=52=25,
∴PQ2+QC2=PC2,
∴∠PQC=90°,
∴△PCQ是直角三角形,
所以②正确;
③∵△BPQ是等边三角形,
∴∠PQB=∠BPQ=60°,
∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°,
所以③正确;
④∠APC=360°-150°-60°-∠QPC=150°-∠QPC,
∵∠PQC=90°,PC≠2QC,
∴∠QPC≠30°,
∴∠APC≠120°.
所以④错误.
所以正确的有①②③.
11.40.
解:如图,过P作PG⊥BF于G,连接PB,
∵AG=30,AP=AB=50,
∴PG=40,
∴BG=80,
∴PB===40.
故这只蚂蚁的最短行程应该是40.
故答案为:40.
12.6+8.
解:过点A作AD⊥BC,垂足为D,
在Rt△ABD中,
∵AB=8,∠B=30°,
∴AD=4,BD=.
在Rt△ACD中,
∵AC=5,AD=4,
∴CD==3,
∴S△ABC=BC×AD=×(3+)×4=6+.
故答案为:6+8.
13.等腰直角三角形.
解:∵各点坐标分别是,和
,根据题意,如下图所示
则:,,
,
∴,,
∴的形状是等腰直角三角形,
故答案是:等腰直角三角形.
14.76
在△ABE中,∵AE=6,BE=8,AB=10,62+82=102,
∴△ABE是直角三角形,
∴S阴影部分=S正方形ABCD﹣S△ABE
=AB2﹣×AE×BE
=100﹣×6×8
=76.
15.4
解:过点C作CE⊥AB于点E,交BD于点F,过点F作FH⊥BC于点H,如图所示:
∵BD平分,
∴,
∴由三角形三边不等关系可得:,即CE的长为的最小值,
∵,
∴△BEC是等腰直角三角形,
∵,
∴,
∴,
∴的最小值为4;
16.3
解:如图所示,在第二象限以OB为边长作等边△BOD,连接OD,并作直线BD,延长BD交x轴于点B'.
∵等边△ABC、等边△BOD
∴AB=BC,BO=BD,∠CBA=∠OBD=60°
∴∠OBA=∠CBD
在△BAO和△BCD中
∴△BAO≌△BCD(SAS)
∴∠AOB=∠BDC=90°
∴CD⊥BD
∴点C随着点B的运动形成的图形是直线CD
∵∠BOB'=90°,∠OBD=60°
∴∠BB'O=30°
∴OB=BB'
∴BD=OB=BB'
∴点D是BB'的中点
∵CD⊥BD
∴CD是BB'的中垂线
∴BC=B′C
∴BC+OC=B'C+OC
又∵点C在直线CD上运动,所以点O、C、B'三点共线时,B'C+OC的值最小,最小值为OB'的长.
在R△BOB'中,∠BOB'=90°,∠OBD=60°,OB=,
BB'=2,OB′=,
∴BC+OC的最小值为3.
17.解:(1)连接,
,,
,
又,,
,
即,
,
.
(2),
,
.
18
解:∵AB=BC=6,边BC在x轴正半轴上,
∴
C(6,0);
过点A作AD⊥OC于点D,
∵△ABC是等边三角形,
∴OD=CD=,OA=BC=6
,
在Rt△AOD中,AD=
,
∴A(3,3)
故点A的坐标为A(3,3),点C的坐标为C(6,0).
19.
解:(1)如图,连接AB,
由题意知AC=500,BC=1200,∠ACB=90°,
在Rt△ABC中,
∵∠ACB=90°,
∴AB2=AC2+BC2=5002+12002=1690000,
∵AB>0
∴AB=1300米;
(2)如图,作点A关于直线MN的对称点A',连接A'B交MN于点P.
驿站到小明家和到小红家距离和的最小值即为A'B,
由题意知AD=200米,A'C⊥MN,
∴A'C=AC+AD+A'D=500+200+200=900米,
在Rt△A'BC中,
∵∠ACB=90°,
∴A'B2=A'C2+BC2=9002+12002=2250000,
∵A'B>0,
∴A'B=1500米,
即从驿站到小明家和到小红家距离和的最小值为1500米.
20.
解:(1)∵AD⊥BC,
∴∠ADB=90°.
在Rt△ABD中,∠ADB=90°,AB=10,BD=8,
∴AD=.
(2)∵AD⊥BC,∠ACD=45°,
∴∠CAD=∠ACD=45°,
∴CD=AD=6,
∴AC=.
21.
解:(1)由题意得:∠BEF=∠DEF;
∵四边形ABCD为长方形,
∴DE∥BF,
∴∠BFE=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF;
(2)∵四边形ABCD为长方形,
∴∠ABF=90°;而∠ABE=18°,
∴∠EBF=90°-18°=72°;
又∵BE=BF,
∴∠BFE的度数=
,
(3)由题意知:BE=DE;
设AE=x,则BE=DE=8-x,
由勾股定理得:
(8-x)2=62+x2,
解得:,
即AE的长为.
22
(1)证明:如图①中,
∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=45°,
∴∠ABD=∠BAD=45°,
∴BD=DA,
∵DF=DC,∠BDF=∠ADC=90°,
∴△BDF≌△ADC(SAS).
∴∠DAC=∠CBE,
∵∠BFD=∠AFE,
∴∠BDF=∠AEF=90°,
∴BE⊥AC.
(2)解:如图,过点D作DM⊥AC,DN⊥BE,
∵△BDF≌△ADC,
∴BF=AC,,
∴DM=DN,
∴ED平分∠BEC,
∴∠BED=∠DEC;
(3)解:如图2-1中,满足条件的点P有3个.
在Rt△ADC中,
∵AD=4,CD=2,
∴AC=,
∵△BDF≌△ADC,
∴BF=AC=,DF=DC=2,BD=AD=4,
当∠PBF=90°,BP=BF时,作PM⊥CB交CB的延长线于M.
易证△PMB≌△BDF,
∴PM=BD=4,
∴点P到直线BC的距离为4;
当∠P′FB=90°,P′F=BF时,作P′H⊥BC于H,FG⊥P′H于G.
易证:P′G=BD=4,GH=DF=2,
∴P′H=4+2=6,
∴P′到直线BC的距离为6;
当∠BP″F=90°,BP″=FP″时,作P″N⊥BC于N.
易证P″N==3,
∴P″到直线BC的距离为3,
综上所述,满足条件的点P到直线BC的距离为4或6或3.
试卷第1页,总3页
勾股定理单元基础练试题
一、单选题
1.下列各组数是勾股数的一组是(
)
A.7,24,25
B.,,
C.1.5,2,2.5
D.32,42,52
2.中,、、的对边分别为、、,若,则有(
)
A.
B.
C.
D.
3.如图,等腰直角三角形ABC中,∠C=90°,腰AC长4,那么点C的坐标是(
)
A.(2,1)
B.(2,2)
C.(2,2)
D.(1,2)
4.如图所示,已知圆柱的底面周长为36,高AB=5,P点位于圆周顶面处,小虫在圆柱侧面爬行,从A点爬到P点,然后再爬回C点,则小虫爬行的最短路程为(
)
A.26
B.13+
C.13
D.2
5.如图,在长方形ABCD中,AB=3,BC=6,对角线AC的垂直平分线分别交AD、AC于点M,N,连接CM,则CM的长为(
)
A.
B.
C.-
D.-
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,则图中所有正方形的面积的和是(
)
A.
B.
C.
D.
7.《九章算术》是我国古代的数学名著,书中有“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部尺远,问折断处离地面的高度是多少?设折断处离地面的高度为尺,则可列方程为(
)
A.
B.
C.
D.
8.四边形中,,则的值为(
)
A.15
B.
C.
D.20
9.如图,中,,,,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则线段的长为(
)
A.
B.
C.
D.
10.如图,P
是等边三角形
ABC
内的一点,且
PA=3,PB=4,PC=5,以
BC
为边在△ABC
外作△BQC≌△BPA,连接
PQ,则以下结论中正确有(
)
①△BPQ
是等边三角形
;
②△PCQ
是直角三角形;③∠APB=150°;④∠APC=120°;
A.①②
B.①③
C.①②③
D.①②④
二、填空题
11.如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=50,点P到AD的距离是30,有一只蚂蚁要从点P爬到点B,则蚂蚁的最短行程为_____.
12.在△ABC中,∠B=30°,AB=8,AC=5,则△ABC的面积为_____.
13.已知直角坐标平面内的点,和,那么的形状是______.
14.如图,点E在正方形ABCD内,AE=6,BE=8,AB=10,则阴影部分的面积为___________.
15.在锐角三角形ABC中,,,BD平分.若M,N分别是边BD,BC上的动点,则的最小值是____.
16.在平面直角坐标系中,己知y轴上一点,A为x轴上的一动点,连接,以为边作等边如图所示,连接,则的最小值是________.
三、解答题
17.已知:如图,四边形ABCD中,AB=BC=1,CD=,AD=1,且∠B=90°.
试求:(1)四边形ABCD的面积.(结果保留根号)
(2)∠BAD的度数.
18.已知等边,AB=BC=6,建立如图所示的直角坐标系,点B和坐标原点O重合,边BC在x轴上,求点A,C的坐标.
19.如图,小明家在一条东西走向的公路北侧米的点处,小红家位于小明家北米(米)、东米(米)点处.
(1)求小明家离小红家的距离;
(2)现要在公路上的点处建一个快递驿站,使最小,请确定点的位置,并求的最小值.
20.如图,在中,,,,.
(1)求线段的长;
(2)求的长.
21.如图,长方形纸片,,将长方形纸片折叠,使点D与点B重合,点C落在点处,折痕为,
(1)求证:.
(2)若,求的度数.
(3)若,,求的长.
22.如图1,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于点F,∠ABC=45°,FD=CD.
(1)请写出BE与AC的位置关系,并说明理由;
(2)如图2,连接DE,求证:∠BED=∠DEC;
(3)若AD=4,CD=2,在直线BC上方的平面内是否存在点P,使得△BFP为等腰直角三角形.若存在,请直接写出点P到直线BC的距离.
参考答案
1.A
解:A、72+242=252,三边是整数,同时能构成直角三角形,故是勾股数,此选项符合题意;
B、,不是正整数,不是勾股数,此选项不合题意;
C、1.5,2.5,不是正整数,不是勾股数,此选项不合题意;
D、92+162≠252,不是勾股数,不合题意.
故选:A.
2.A
,
∴是直角三角形,且,
故选:A.
3.C
解:过C作CD⊥AB于D,如图所示:
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB==AC=4,AD=BD=AB=2,
∴CD=AB=AD=2,
∴点C的坐标是(2,2),
4.B
解:如图,
根据题意,AB=CD=5,AC=BD=,
∵P点位于圆周顶面处,
∴DP=BD=6,则BP=BD-DP=12,
∴小虫爬行的最短路程.
故选:B.
5.A
解:∵四边形ABCD是矩形,
∴∠D=∠B=90°,AD=BC=6,AB=DC=3,
∵MN是AC的垂直平分线,
∴AM=CM,
∴DM=AD-AM=AD-CM=6-CM,
在Rt△DMC中,由勾股定理得:DM2+DC2=CM2,
(6-CM)2+32=CM2,
解得:CM=,
6.D
解:如图,设正方形A、B、C、D、E、F的边长分别为a、b、c、d、x、f
所有的三角形都是直角三角形
由勾股定理可得,,
S正方形A+S正方形B=S正方形E,S正方形C+S正方形D=S正方形F,S正方形E+S正方形F=64
S正方形A+S正方形B+
S正方形C+S正方形D+
S正方形E+S正方形F+82
=2(S正方形E+S正方形F)+64
=264+64
=192(cm2)
所有的正方形的面积和是192cm2
7.D
解:设折断处离地面的高度为尺,则斜边为(10-x)尺,
根据勾股定理得:,
8.D
解:如图,把△ABC绕点A逆时针旋转90°得到△ADE,连接CE,作EM⊥CD于M,
则AC=AE=,∠CAE=90°,∠ADE=∠ABC,DE=BC=12,
在Rt△ACE中,CE=,
∵∠BAD=90°,∠BCD=30°,
∴∠ABC+∠ADC=360°-30°-90°=240°,
∴∠ADE+∠ADC=240°,
∴∠CDE=120°,即∠EDM=60°,
∴在Rt△EDM中,∠DEM=30°
∴,
在Rt△CEM中,设CD=x,则CM=6+x
∴,解得:(舍去),
∴CD=20
故选:D
9.A
解:∵Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5,
根据折叠的性质可知AC=CD,∠A=∠CDE,CE⊥AB,
∴B′D=BC﹣CD=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FD=90°,
∵S△ABC=AC?BC=AB?CE,
∴AC?BC=AB?CE,
∴CE=,
∴EF=,ED=AE=,
∴DF=EF﹣ED=
∴B′F=.
选:A.
10.C
解:①∵△ABC是等边三角形,
∴∠ABC=60°,
∵△BQC≌△BPA,
∴∠CBQ=∠ABP,PB=QB=4,
PA=QC=3,∠BPA=∠BQC,
∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,
∴△BPQ是等边三角形,
所以①正确;
②PQ=PB=4,
PQ2+QC2=42+32=25,
PC2=52=25,
∴PQ2+QC2=PC2,
∴∠PQC=90°,
∴△PCQ是直角三角形,
所以②正确;
③∵△BPQ是等边三角形,
∴∠PQB=∠BPQ=60°,
∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°,
所以③正确;
④∠APC=360°-150°-60°-∠QPC=150°-∠QPC,
∵∠PQC=90°,PC≠2QC,
∴∠QPC≠30°,
∴∠APC≠120°.
所以④错误.
所以正确的有①②③.
11.40.
解:如图,过P作PG⊥BF于G,连接PB,
∵AG=30,AP=AB=50,
∴PG=40,
∴BG=80,
∴PB===40.
故这只蚂蚁的最短行程应该是40.
故答案为:40.
12.6+8.
解:过点A作AD⊥BC,垂足为D,
在Rt△ABD中,
∵AB=8,∠B=30°,
∴AD=4,BD=.
在Rt△ACD中,
∵AC=5,AD=4,
∴CD==3,
∴S△ABC=BC×AD=×(3+)×4=6+.
故答案为:6+8.
13.等腰直角三角形.
解:∵各点坐标分别是,和
,根据题意,如下图所示
则:,,
,
∴,,
∴的形状是等腰直角三角形,
故答案是:等腰直角三角形.
14.76
在△ABE中,∵AE=6,BE=8,AB=10,62+82=102,
∴△ABE是直角三角形,
∴S阴影部分=S正方形ABCD﹣S△ABE
=AB2﹣×AE×BE
=100﹣×6×8
=76.
15.4
解:过点C作CE⊥AB于点E,交BD于点F,过点F作FH⊥BC于点H,如图所示:
∵BD平分,
∴,
∴由三角形三边不等关系可得:,即CE的长为的最小值,
∵,
∴△BEC是等腰直角三角形,
∵,
∴,
∴,
∴的最小值为4;
16.3
解:如图所示,在第二象限以OB为边长作等边△BOD,连接OD,并作直线BD,延长BD交x轴于点B'.
∵等边△ABC、等边△BOD
∴AB=BC,BO=BD,∠CBA=∠OBD=60°
∴∠OBA=∠CBD
在△BAO和△BCD中
∴△BAO≌△BCD(SAS)
∴∠AOB=∠BDC=90°
∴CD⊥BD
∴点C随着点B的运动形成的图形是直线CD
∵∠BOB'=90°,∠OBD=60°
∴∠BB'O=30°
∴OB=BB'
∴BD=OB=BB'
∴点D是BB'的中点
∵CD⊥BD
∴CD是BB'的中垂线
∴BC=B′C
∴BC+OC=B'C+OC
又∵点C在直线CD上运动,所以点O、C、B'三点共线时,B'C+OC的值最小,最小值为OB'的长.
在R△BOB'中,∠BOB'=90°,∠OBD=60°,OB=,
BB'=2,OB′=,
∴BC+OC的最小值为3.
17.解:(1)连接,
,,
,
又,,
,
即,
,
.
(2),
,
.
18
解:∵AB=BC=6,边BC在x轴正半轴上,
∴
C(6,0);
过点A作AD⊥OC于点D,
∵△ABC是等边三角形,
∴OD=CD=,OA=BC=6
,
在Rt△AOD中,AD=
,
∴A(3,3)
故点A的坐标为A(3,3),点C的坐标为C(6,0).
19.
解:(1)如图,连接AB,
由题意知AC=500,BC=1200,∠ACB=90°,
在Rt△ABC中,
∵∠ACB=90°,
∴AB2=AC2+BC2=5002+12002=1690000,
∵AB>0
∴AB=1300米;
(2)如图,作点A关于直线MN的对称点A',连接A'B交MN于点P.
驿站到小明家和到小红家距离和的最小值即为A'B,
由题意知AD=200米,A'C⊥MN,
∴A'C=AC+AD+A'D=500+200+200=900米,
在Rt△A'BC中,
∵∠ACB=90°,
∴A'B2=A'C2+BC2=9002+12002=2250000,
∵A'B>0,
∴A'B=1500米,
即从驿站到小明家和到小红家距离和的最小值为1500米.
20.
解:(1)∵AD⊥BC,
∴∠ADB=90°.
在Rt△ABD中,∠ADB=90°,AB=10,BD=8,
∴AD=.
(2)∵AD⊥BC,∠ACD=45°,
∴∠CAD=∠ACD=45°,
∴CD=AD=6,
∴AC=.
21.
解:(1)由题意得:∠BEF=∠DEF;
∵四边形ABCD为长方形,
∴DE∥BF,
∴∠BFE=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF;
(2)∵四边形ABCD为长方形,
∴∠ABF=90°;而∠ABE=18°,
∴∠EBF=90°-18°=72°;
又∵BE=BF,
∴∠BFE的度数=
,
(3)由题意知:BE=DE;
设AE=x,则BE=DE=8-x,
由勾股定理得:
(8-x)2=62+x2,
解得:,
即AE的长为.
22
(1)证明:如图①中,
∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=45°,
∴∠ABD=∠BAD=45°,
∴BD=DA,
∵DF=DC,∠BDF=∠ADC=90°,
∴△BDF≌△ADC(SAS).
∴∠DAC=∠CBE,
∵∠BFD=∠AFE,
∴∠BDF=∠AEF=90°,
∴BE⊥AC.
(2)解:如图,过点D作DM⊥AC,DN⊥BE,
∵△BDF≌△ADC,
∴BF=AC,,
∴DM=DN,
∴ED平分∠BEC,
∴∠BED=∠DEC;
(3)解:如图2-1中,满足条件的点P有3个.
在Rt△ADC中,
∵AD=4,CD=2,
∴AC=,
∵△BDF≌△ADC,
∴BF=AC=,DF=DC=2,BD=AD=4,
当∠PBF=90°,BP=BF时,作PM⊥CB交CB的延长线于M.
易证△PMB≌△BDF,
∴PM=BD=4,
∴点P到直线BC的距离为4;
当∠P′FB=90°,P′F=BF时,作P′H⊥BC于H,FG⊥P′H于G.
易证:P′G=BD=4,GH=DF=2,
∴P′H=4+2=6,
∴P′到直线BC的距离为6;
当∠BP″F=90°,BP″=FP″时,作P″N⊥BC于N.
易证P″N==3,
∴P″到直线BC的距离为3,
综上所述,满足条件的点P到直线BC的距离为4或6或3.
试卷第1页,总3页
