2020-2021学年七年级数学北师大版下册第二章两条直线的位置关系同步复习学案(含练习,无答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册第二章两条直线的位置关系同步复习学案(含练习,无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 235.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 12:19:52 | ||
图片预览

文档简介
北师大版七年级数学第二章
2.1 两条直线的位置关系同步复习题
知识点1:相交线和平行线的概念
相交线:只有一个公共点的两条直线为相交线
平行线:在同一个平面内,不相交的两条直线为平行线
注意:1、两条直线的公共点叫做交点,两条直线相交构成4个小于平角的角
用定义法判断两条线是否平行,一看是否在同一平面,二看有无交点,三看是否是直线,三点缺一不可
练习:
1.在同一个平面内,不重合的两条直线的位置关系可能是 ( )
A.相交或平行 B.相交或垂直 C.平行或垂直 D.不能确定
下列说法中正确的是( )
A.不相交的两条直线是平行线
B.在同一平面内,不相交的两个射线叫做平行线
C.在同一平面内,两条直线不相交就重合
D.在同一平面内,没有公共点的两条直线是平行线
知识点2:对顶角的概念及性质
形成对顶角的条件:1、两个角有公共顶点;2、两个角的两边分别互为反向延长线
对顶角的性质:对顶角相等
练习:
3.四条直线相交于一点,总共有对顶角( )
A.8对 B.10对 C.4对 D.12对
4.
知识点3:补角、余角的概念
补角:如果两个角的和是180度,那么称这两个角互为补角
余角:如果两个角的和是90度,那么称这两个角互为余角
注:互为补角或余角是指两个角之间特定的数量关系,而补角或余角是一个角相对于另一个角而言的
练习
5.如果一个角是36°,那么( )
它的余角是64° B.它的补角是64° C.它的余角是144° D.它的补角是144°
6.∠1 与∠2 互余且相等,∠1 与∠3 是邻补角,则∠3 的大小是( )
A.30° B.105° C.120° D.135°
7.已知∠A=25°,则∠A的余角是 ( )
A.65° B.75° C.155° D.165°
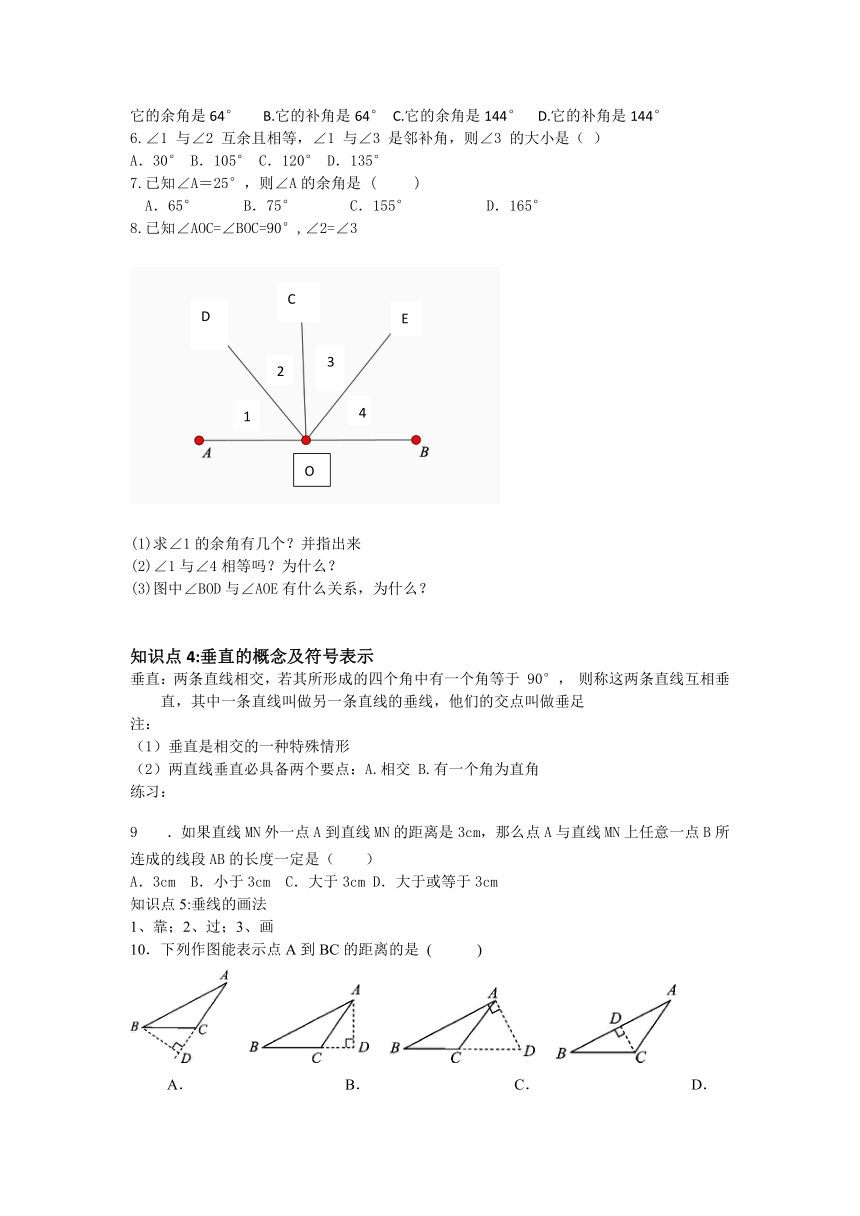
已知∠AOC=∠BOC=90°,∠2=∠3
求∠1的余角有几个?并指出来
∠1与∠4相等吗?为什么?
图中∠BOD与∠AOE有什么关系,为什么?
知识点4:垂直的概念及符号表示
垂直:两条直线相交,若其所形成的四个角中有一个角等于 90°, 则称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,他们的交点叫做垂足
注:
(1)垂直是相交的一种特殊情形
(2)两直线垂直必具备两个要点:A.相交 B.有一个角为直角
练习:
9.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm C.大于3cm D.大于或等于3cm
知识点5:垂线的画法
1、靠;2、过;3、画
10.下列作图能表示点A到BC的距离的是 ( )
A. B. C. D.
知识点6:垂线的性质和点到直线的距离
(1)在平面门内,过一点有且只有一条直线与已知直线垂直
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短
注意:垂线是直线,垂线段是线段
练习:
下列说法正确的是( )
A.过直线l外两点A、B,一定可以画一条直线与直线l垂直
B.过直线上一点和直线外一点一定可以画这条直线的垂线
C.过射线外一点可以画这条射线的一条垂线
D.同一平面如果两个直线不相交,那么这两条直线有可能垂直
12.如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为 ( )
① AB与AC互相垂直;② AD与AC互相垂直;③ 点C到AB的垂线段是线段AB;
④ 点A到BC的距离是线段AD;⑤ 线段AB的长度是点B到AC的距离;
⑥ 线段AB是点B到AC的距离.
A.2个 B.3个 C.4个 D.5个
13.将两块直角三角板的直角顶点重合为如图所示的形状,若∠AOD=120°,则∠BOC= ;
14.如图,要从小河引水到村庄A,请设计并作出一最佳路线,理由是_____.
综合练习:
如图,已知:直线AB与CD相交于点O,∠1=50度.求:∠2和∠3的度数.
16.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
如图,直线AB、CD相交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,求∠AOE和∠DOF的度数.
18.一个角的补角加上10°后,等于这个角的余角的3倍,求这个角;
2.1 两条直线的位置关系同步复习题
知识点1:相交线和平行线的概念
相交线:只有一个公共点的两条直线为相交线
平行线:在同一个平面内,不相交的两条直线为平行线
注意:1、两条直线的公共点叫做交点,两条直线相交构成4个小于平角的角
用定义法判断两条线是否平行,一看是否在同一平面,二看有无交点,三看是否是直线,三点缺一不可
练习:
1.在同一个平面内,不重合的两条直线的位置关系可能是 ( )
A.相交或平行 B.相交或垂直 C.平行或垂直 D.不能确定
下列说法中正确的是( )
A.不相交的两条直线是平行线
B.在同一平面内,不相交的两个射线叫做平行线
C.在同一平面内,两条直线不相交就重合
D.在同一平面内,没有公共点的两条直线是平行线
知识点2:对顶角的概念及性质
形成对顶角的条件:1、两个角有公共顶点;2、两个角的两边分别互为反向延长线
对顶角的性质:对顶角相等
练习:
3.四条直线相交于一点,总共有对顶角( )
A.8对 B.10对 C.4对 D.12对
4.
知识点3:补角、余角的概念
补角:如果两个角的和是180度,那么称这两个角互为补角
余角:如果两个角的和是90度,那么称这两个角互为余角
注:互为补角或余角是指两个角之间特定的数量关系,而补角或余角是一个角相对于另一个角而言的
练习
5.如果一个角是36°,那么( )
它的余角是64° B.它的补角是64° C.它的余角是144° D.它的补角是144°
6.∠1 与∠2 互余且相等,∠1 与∠3 是邻补角,则∠3 的大小是( )
A.30° B.105° C.120° D.135°
7.已知∠A=25°,则∠A的余角是 ( )
A.65° B.75° C.155° D.165°
已知∠AOC=∠BOC=90°,∠2=∠3
求∠1的余角有几个?并指出来
∠1与∠4相等吗?为什么?
图中∠BOD与∠AOE有什么关系,为什么?
知识点4:垂直的概念及符号表示
垂直:两条直线相交,若其所形成的四个角中有一个角等于 90°, 则称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,他们的交点叫做垂足
注:
(1)垂直是相交的一种特殊情形
(2)两直线垂直必具备两个要点:A.相交 B.有一个角为直角
练习:
9.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm C.大于3cm D.大于或等于3cm
知识点5:垂线的画法
1、靠;2、过;3、画
10.下列作图能表示点A到BC的距离的是 ( )
A. B. C. D.
知识点6:垂线的性质和点到直线的距离
(1)在平面门内,过一点有且只有一条直线与已知直线垂直
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短
注意:垂线是直线,垂线段是线段
练习:
下列说法正确的是( )
A.过直线l外两点A、B,一定可以画一条直线与直线l垂直
B.过直线上一点和直线外一点一定可以画这条直线的垂线
C.过射线外一点可以画这条射线的一条垂线
D.同一平面如果两个直线不相交,那么这两条直线有可能垂直
12.如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为 ( )
① AB与AC互相垂直;② AD与AC互相垂直;③ 点C到AB的垂线段是线段AB;
④ 点A到BC的距离是线段AD;⑤ 线段AB的长度是点B到AC的距离;
⑥ 线段AB是点B到AC的距离.
A.2个 B.3个 C.4个 D.5个
13.将两块直角三角板的直角顶点重合为如图所示的形状,若∠AOD=120°,则∠BOC= ;
14.如图,要从小河引水到村庄A,请设计并作出一最佳路线,理由是_____.
综合练习:
如图,已知:直线AB与CD相交于点O,∠1=50度.求:∠2和∠3的度数.
16.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
如图,直线AB、CD相交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,求∠AOE和∠DOF的度数.
18.一个角的补角加上10°后,等于这个角的余角的3倍,求这个角;
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
