2020—2021学年人教版八年级数学下册第 18.2.3 正方形 分正方形(共15张ppt)
文档属性
| 名称 | 2020—2021学年人教版八年级数学下册第 18.2.3 正方形 分正方形(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 21:34:28 | ||
图片预览


文档简介
(共15张PPT)
在数学的天地里,重要的不是我们知道什么,
更重要的是我们应该
怎么知道什么。
——毕达哥拉斯
18.2.3
正方形
矩
形
正方形
〃
〃
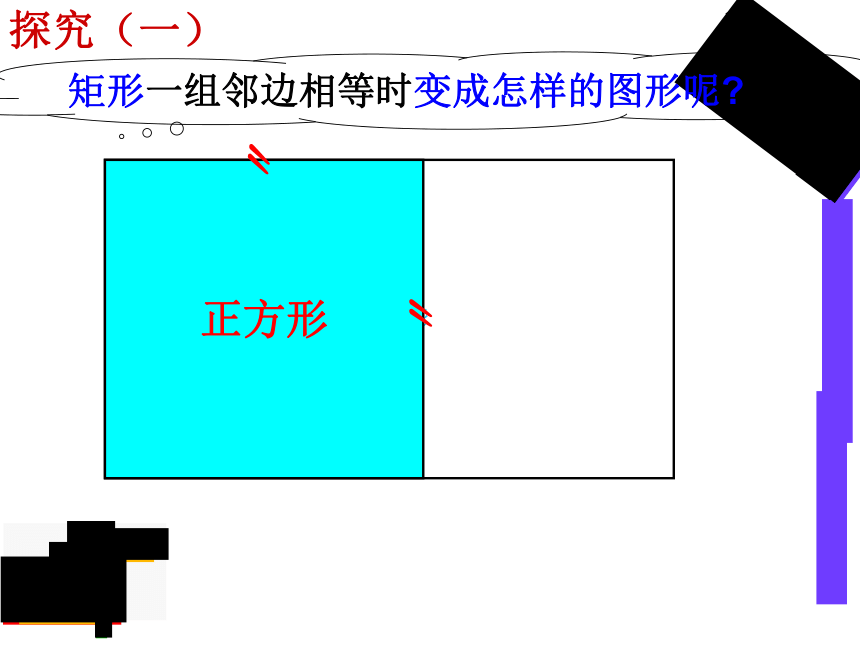
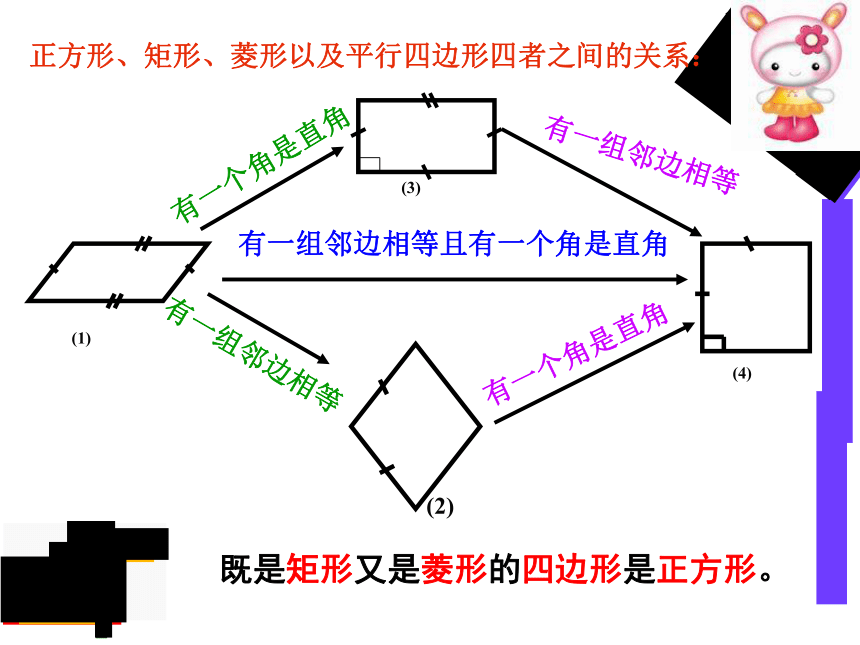
矩形一组邻边相等时变成怎样的图形呢?
探究(一)
菱
形
∟
∟
∟
∟
正方形
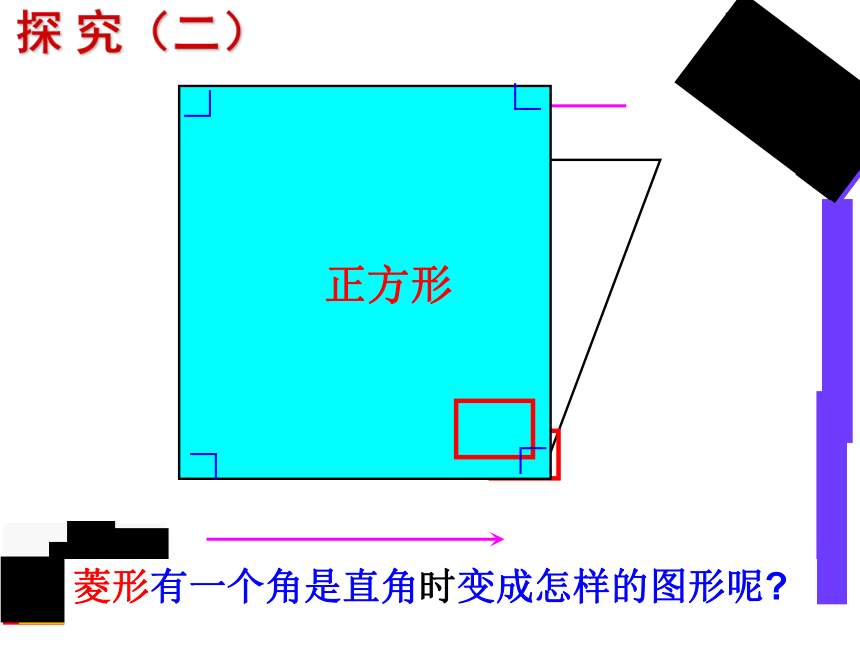
探
究(二)
菱形有一个角是直角时变成怎样的图形呢?
一个角是直角
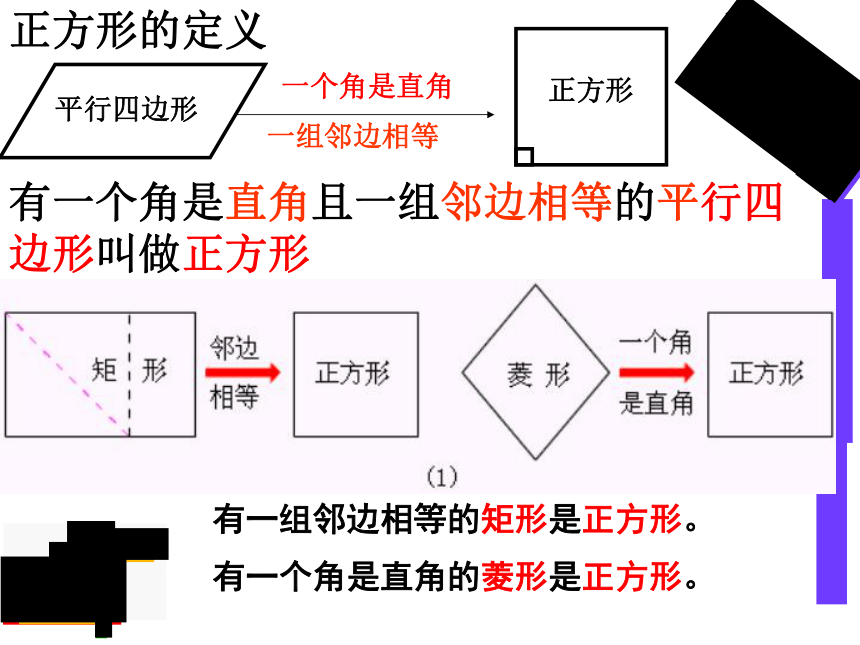
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形
平行四边形
正方形的定义
一组邻边相等
有一个角是直角的菱形是正方形。
有一组邻边相等的矩形是正方形。
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)
(2)
(3)
(4)
正方形、矩形、菱形以及平行四边形四者之间的关系:
既是矩形又是菱形的四边形是正方形。
正方形是特殊的矩形,也是特殊的菱形,既具有矩形的性质又具有菱形的性质。那么它有哪些性质呢?
正方形性质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行,
四条边都相等
四
个
角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD
AD∥BC,
AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OB=OC=OD,
∠1=
∠2=
∠3=
∠4=
∠5=
∠6=
∠7=
∠8
轴对称图形
中心对称图形
1
2
3
4
5
6
7
8
正方形具有而矩形不一定具有的性质是(
)
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.
选一选
2.正方形具有而菱形不一定具有的性质(
)
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
例1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
O
A
B
C
D
已知:四边形ABCD是矩形,对角线AC、BD相交于点O.
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:∵四边形ABCD是正方形
并且△ABO≌△BCO≌△CDO≌△DAO
∴
△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,
∴AC=BD,AC⊥BD,AO=CO=BO=DO.
45°
正方形
12cm
1.正方形的一边和对角线的夹角为______.
2.如果一个四边形既是菱形又是矩形,那么它一定是_________.
3.已知正方形的面积为9cm,它的周长为
______.
练一练
4.已知四边形ABCD是菱形,若___________
则四边形ABCD是正方形(添加一个条件)
∠A=90°(或AC=BD)
5.已知四边形ABCD是矩形,若___________
则四边形ABCD是正方形(添加一个条件)
AB=AD(或AC
⊥
BD)
四边形
平行四边形
矩形
菱形
正方形
平行四边形
矩形
四边形
菱形
正
方
形
四边形、平行四边形、矩形、菱形、正方形之间关系
谈谈收获
1、自评:我学到了什么?
2、互评:你或他学到了什么?
3、你还有什么疑惑?
作业
习题18.2
必做题12、13、选做题15
同学们再见!
在数学的天地里,重要的不是我们知道什么,
更重要的是我们应该
怎么知道什么。
——毕达哥拉斯
18.2.3
正方形
矩
形
正方形
〃
〃
矩形一组邻边相等时变成怎样的图形呢?
探究(一)
菱
形
∟
∟
∟
∟
正方形
探
究(二)
菱形有一个角是直角时变成怎样的图形呢?
一个角是直角
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形
平行四边形
正方形的定义
一组邻边相等
有一个角是直角的菱形是正方形。
有一组邻边相等的矩形是正方形。
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)
(2)
(3)
(4)
正方形、矩形、菱形以及平行四边形四者之间的关系:
既是矩形又是菱形的四边形是正方形。
正方形是特殊的矩形,也是特殊的菱形,既具有矩形的性质又具有菱形的性质。那么它有哪些性质呢?
正方形性质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行,
四条边都相等
四
个
角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD
AD∥BC,
AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OB=OC=OD,
∠1=
∠2=
∠3=
∠4=
∠5=
∠6=
∠7=
∠8
轴对称图形
中心对称图形
1
2
3
4
5
6
7
8
正方形具有而矩形不一定具有的性质是(
)
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.
选一选
2.正方形具有而菱形不一定具有的性质(
)
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
例1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
O
A
B
C
D
已知:四边形ABCD是矩形,对角线AC、BD相交于点O.
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:∵四边形ABCD是正方形
并且△ABO≌△BCO≌△CDO≌△DAO
∴
△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,
∴AC=BD,AC⊥BD,AO=CO=BO=DO.
45°
正方形
12cm
1.正方形的一边和对角线的夹角为______.
2.如果一个四边形既是菱形又是矩形,那么它一定是_________.
3.已知正方形的面积为9cm,它的周长为
______.
练一练
4.已知四边形ABCD是菱形,若___________
则四边形ABCD是正方形(添加一个条件)
∠A=90°(或AC=BD)
5.已知四边形ABCD是矩形,若___________
则四边形ABCD是正方形(添加一个条件)
AB=AD(或AC
⊥
BD)
四边形
平行四边形
矩形
菱形
正方形
平行四边形
矩形
四边形
菱形
正
方
形
四边形、平行四边形、矩形、菱形、正方形之间关系
谈谈收获
1、自评:我学到了什么?
2、互评:你或他学到了什么?
3、你还有什么疑惑?
作业
习题18.2
必做题12、13、选做题15
同学们再见!
