2020-2021学年人教版八年级下册数学 19.1函数 同步练习 (word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 19.1函数 同步练习 (word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 91.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览

文档简介
19.1函数
同步练习
一.选择题
1.下列解析式中,y不是x的函数的是( )
A.y=2x
B.y=x2
C.y=±
(x>0)
D.y=|x|
2.函数y=中自变量x的取值范围是( )
A.x>2
B.x≤2
C.x≥2
D.x≠2
3.下列关系中,y不是x的函数关系的是( )
A.长方形的长一定时,其面积y与宽x
B.高速公路上匀速行驶的汽车,其行驶的路程y与行驶的时间x
C.y=|x|
D.|y|=x
4.要画一个面积为15cm2的长方形,其长为xcm,宽为ycm,在这一变化过程中,常量与变量分别是( )
A.常量为15;变量为x,y
B.常量为15,y;变量为x
C.常量为15,x;变量为y
D.常量为x,y;变量为15
5.一列火车从A站行驶3公里到B处以后,以每小时90公里的速度前进.则离开B处t小时后,火车离A站的路程s与时间t的关系是( )
A.s=3+90t
B.s=90t
C.s=3t
D.s=90+3t
6.如图为有春蛋糕店的价目表,阿凯原本拿了4个蛋糕去结账,结账时发现该点正在举办优惠活动,优惠方式为每买5个蛋糕,其中1个价格最低的蛋糕免费,因此阿凯后来多买了1个黑樱桃蛋糕.若阿凯原本的结账金额为x元,后来的结账金额为y元,则x与y的关系式不可能为下列何者?( )
A.y=x
B.y=x+5
C.y=x+10
D.y=x+15
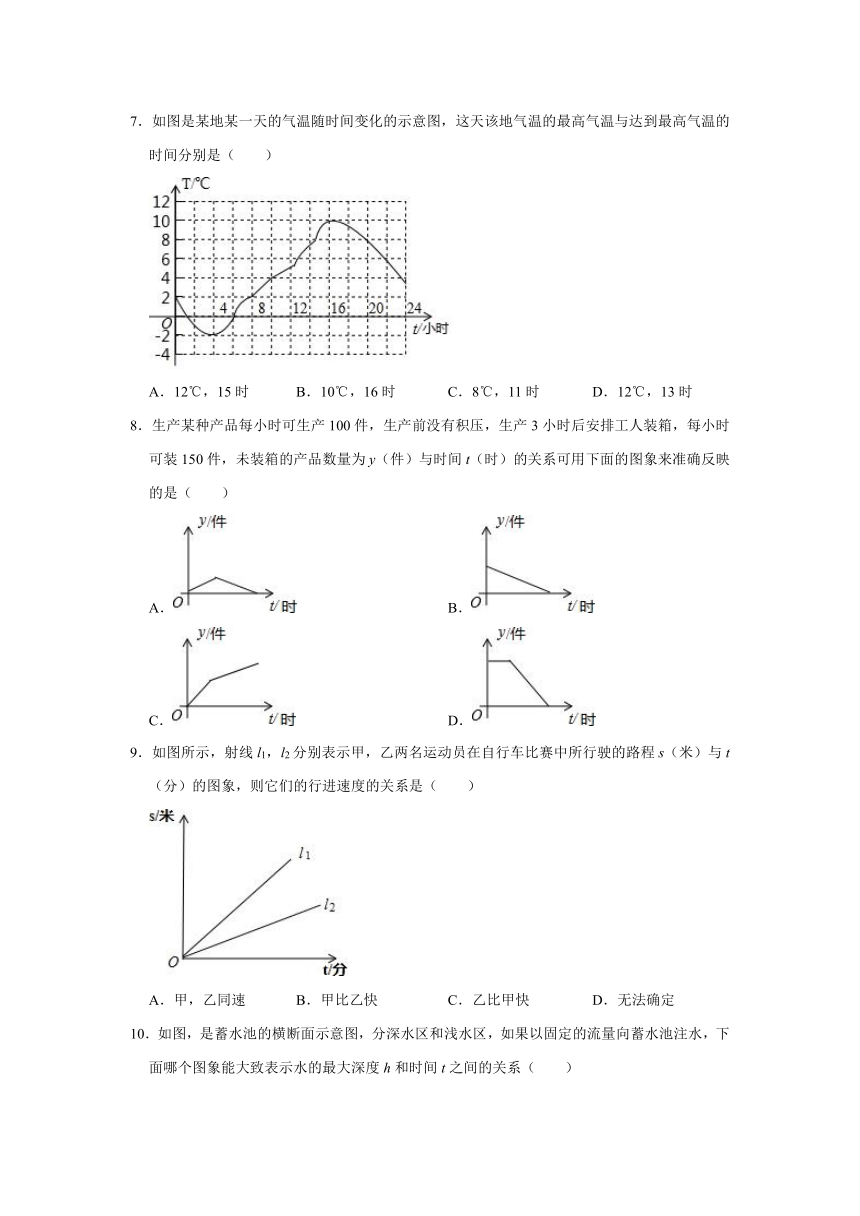
7.如图是某地某一天的气温随时间变化的示意图,这天该地气温的最高气温与达到最高气温的时间分别是( )
A.12℃,15时
B.10℃,16时
C.8℃,11时
D.12℃,13时
8.生产某种产品每小时可生产100件,生产前没有积压,生产3小时后安排工人装箱,每小时可装150件,未装箱的产品数量为y(件)与时间t(时)的关系可用下面的图象来准确反映的是( )
A.
B.
C.
D.
9.如图所示,射线l1,l2分别表示甲,乙两名运动员在自行车比赛中所行驶的路程s(米)与t(分)的图象,则它们的行进速度的关系是( )
A.甲,乙同速
B.甲比乙快
C.乙比甲快
D.无法确定
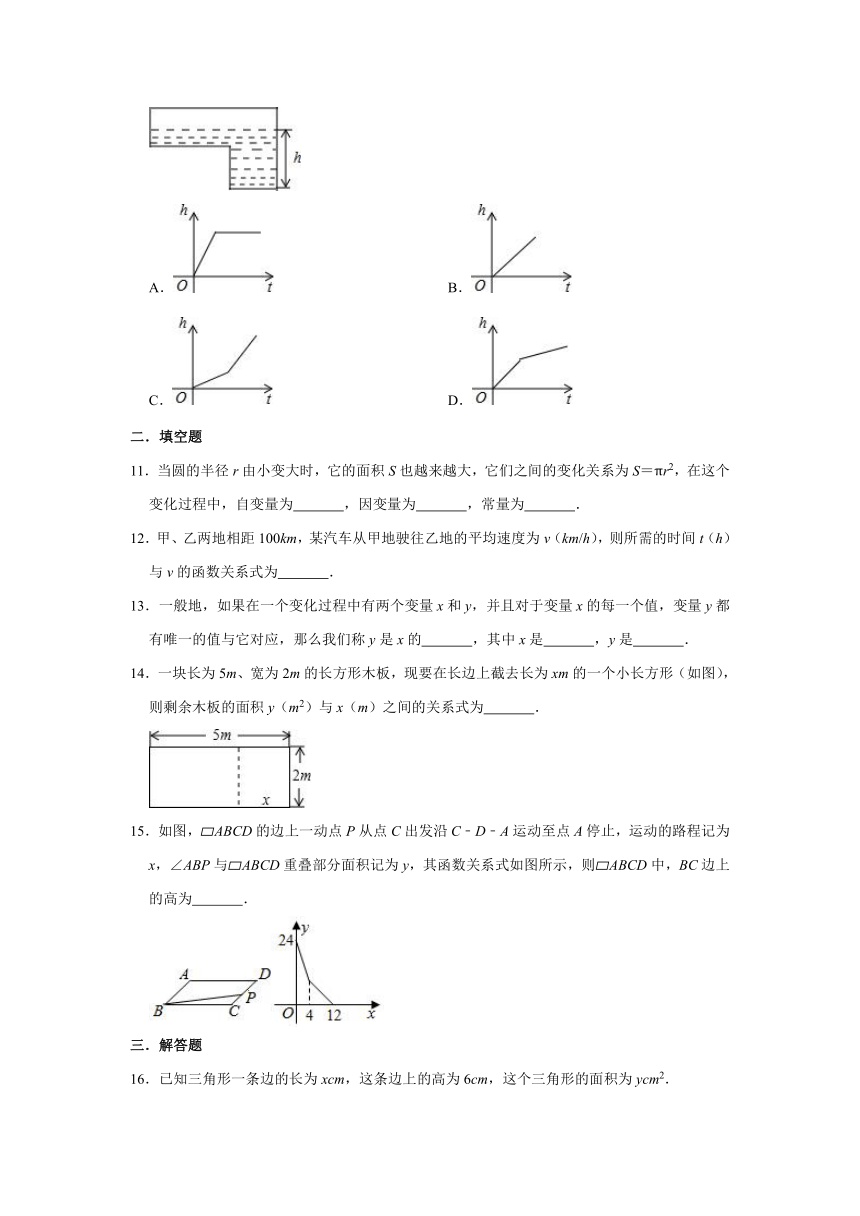
10.如图,是蓄水池的横断面示意图,分深水区和浅水区,如果以固定的流量向蓄水池注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )
A.
B.
C.
D.
二.填空题
11.当圆的半径r由小变大时,它的面积S也越来越大,它们之间的变化关系为S=πr2,在这个变化过程中,自变量为
,因变量为
,常量为
.
12.甲、乙两地相距100km,某汽车从甲地驶往乙地的平均速度为v(km/h),则所需的时间t(h)与v的函数关系式为
.
13.一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的
,其中x是
,y是
.
14.一块长为5m、宽为2m的长方形木板,现要在长边上截去长为xm的一个小长方形(如图),则剩余木板的面积y(m2)与x(m)之间的关系式为
.
15.如图,?ABCD的边上一动点P从点C出发沿C﹣D﹣A运动至点A停止,运动的路程记为x,∠ABP与?ABCD重叠部分面积记为y,其函数关系式如图所示,则?ABCD中,BC边上的高为
.
三.解答题
16.已知三角形一条边的长为xcm,这条边上的高为6cm,这个三角形的面积为ycm2.
(1)写出y与x的函数表达式;
(2)画出这个函数的图象.
17.求下列函数中自变量x的取值范围.
(1)y=﹣x;
(2)y=x+;
(3)y=;
(4)y=.
18.如表是某校高中毕业生升入高等学校人数比率的统计表:
年份
2003
2004
2005
2006
2007
2008
2009
2010
升学率
43.3%
49.9%
418.6%
46.1%
63.8%
73.2%
78.8%
83.5%
(1)其中有哪些变量?
(2)可以把其中的哪个变量看做另一个变量的函数?
参考答案
一.选择题
1.解:A、y=2x对于x的每一个取值,y都有唯一确定的值,符合函数的定义;
B、y=x2对于x的每一个取值,y都有唯一确定的值,符合函数的定义;
C、y=±
(x>0)对于x的每一个取值,y有两个确定的值,不符合函数的定义;
D、y=|x|对于x的每一个取值,y都有唯一确定的值,符合函数的定义.
故选:C.
2.解:由题意得,2﹣x≥0,
解得x≤2.
故选:B.
3.解:A、∵对于x的每一个取值,y都有唯一确定的值,故A正确;
B、∵对于x的每一个取值,y都有唯一确定的值,故B正确;
C、∵对于x的每一个取值,y都有唯一确定的值,故C正确;
D、∵对于x的每一个取值,y没有唯一确定的值,故D错误;
故选:D.
4.解:由题意,得
xy=15
常量为15,变量为x,y.
故选:A.
5.解:火车离A站的距离等于先行的3公理,加上后来t小时行驶的距离可得,
s=3+90t,
故选:A.
6.解:阿凯原本拿了4个蛋糕去结账,后来多买了一个50元的黑樱桃蛋糕,优惠方式为:价格最低的蛋糕免费.
①若原本四个蛋糕中最便宜的蛋糕价格等于50元或高于50元,最后买的黑樱桃蛋糕的最便宜的,免费,
∴此时原本结账金额等于后来结账的金额,即y=x;
②如果原本四个蛋糕中最便宜的蛋糕价格低于50元,则这个最便宜的蛋糕就变成免费,改以黑樱桃蛋糕计费,价格发生变化.
如果原本四个蛋糕中最便宜的是40元(伯爵茶蛋糕),买了黑樱桃蛋糕后,伯爵茶蛋糕变成免费,需要付黑樱桃蛋糕,多付10元,
此时,y=x+10;
③如果原本四个蛋糕中最便宜的是45元,买了黑樱桃蛋糕后,多付5元,
此时,y=x+5.
故选:D.
7.解:由图象可知,这一天中最高气温10°C,达到最高气温的时刻是16时.
故选:B.
8.解:根据题意可知:生产前没有积压代表图象从0开始,生产3小时后安排工人装箱每小时可装150件代表图象匀速上升到一定程度开始下匀速降为0.
故选:A.
9.解:相同的路程,甲用的时间短,那么甲的速度一定快.
故选:B.
10.解:根据题意和图形的形状,可知水的最大深度h与时间t之间的关系分为两段,先快后慢,
故选:D.
二.填空题
11.解:圆的半径发生变化时,面积也发生变化,圆面积S与半径r的关系为S=πr2,r是自变量,S是变量,π是常量.
故答案为:r,S,π.
12.解:由时间=路程÷速度可得,
t=,
故答案为:t=.
13.解:一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
故答案为:函数,自变量,因变量.
14.解:依题意有:y=2×5﹣2x=10﹣2x.
故答案为:y=10﹣2x.
15.解:观察图象可知;CD=4,AD=BC=8,设BC边上的高为h,
由题意:BC?h=24,
∴8h=24,
∴h=3,
故答案为:3.
三.解答题
16.解:(1)由题意,得:y==3x(x≥0);
(2)函数的图象如下所示:
17.解:(1)自变量的取值范围是全体实数;
(2)∵3x≠0,
∴x≠0;
(3)∵2x﹣1≠0,
∴x≠;
(4)∵x+4≠0,
∴x≠﹣4.
18.解:(1)由题可得变量为:年份和升学率;
(2)可以把其中的升学率看做年份的函数.
同步练习
一.选择题
1.下列解析式中,y不是x的函数的是( )
A.y=2x
B.y=x2
C.y=±
(x>0)
D.y=|x|
2.函数y=中自变量x的取值范围是( )
A.x>2
B.x≤2
C.x≥2
D.x≠2
3.下列关系中,y不是x的函数关系的是( )
A.长方形的长一定时,其面积y与宽x
B.高速公路上匀速行驶的汽车,其行驶的路程y与行驶的时间x
C.y=|x|
D.|y|=x
4.要画一个面积为15cm2的长方形,其长为xcm,宽为ycm,在这一变化过程中,常量与变量分别是( )
A.常量为15;变量为x,y
B.常量为15,y;变量为x
C.常量为15,x;变量为y
D.常量为x,y;变量为15
5.一列火车从A站行驶3公里到B处以后,以每小时90公里的速度前进.则离开B处t小时后,火车离A站的路程s与时间t的关系是( )
A.s=3+90t
B.s=90t
C.s=3t
D.s=90+3t
6.如图为有春蛋糕店的价目表,阿凯原本拿了4个蛋糕去结账,结账时发现该点正在举办优惠活动,优惠方式为每买5个蛋糕,其中1个价格最低的蛋糕免费,因此阿凯后来多买了1个黑樱桃蛋糕.若阿凯原本的结账金额为x元,后来的结账金额为y元,则x与y的关系式不可能为下列何者?( )
A.y=x
B.y=x+5
C.y=x+10
D.y=x+15
7.如图是某地某一天的气温随时间变化的示意图,这天该地气温的最高气温与达到最高气温的时间分别是( )
A.12℃,15时
B.10℃,16时
C.8℃,11时
D.12℃,13时
8.生产某种产品每小时可生产100件,生产前没有积压,生产3小时后安排工人装箱,每小时可装150件,未装箱的产品数量为y(件)与时间t(时)的关系可用下面的图象来准确反映的是( )
A.
B.
C.
D.
9.如图所示,射线l1,l2分别表示甲,乙两名运动员在自行车比赛中所行驶的路程s(米)与t(分)的图象,则它们的行进速度的关系是( )
A.甲,乙同速
B.甲比乙快
C.乙比甲快
D.无法确定
10.如图,是蓄水池的横断面示意图,分深水区和浅水区,如果以固定的流量向蓄水池注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )
A.
B.
C.
D.
二.填空题
11.当圆的半径r由小变大时,它的面积S也越来越大,它们之间的变化关系为S=πr2,在这个变化过程中,自变量为
,因变量为
,常量为
.
12.甲、乙两地相距100km,某汽车从甲地驶往乙地的平均速度为v(km/h),则所需的时间t(h)与v的函数关系式为
.
13.一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的
,其中x是
,y是
.
14.一块长为5m、宽为2m的长方形木板,现要在长边上截去长为xm的一个小长方形(如图),则剩余木板的面积y(m2)与x(m)之间的关系式为
.
15.如图,?ABCD的边上一动点P从点C出发沿C﹣D﹣A运动至点A停止,运动的路程记为x,∠ABP与?ABCD重叠部分面积记为y,其函数关系式如图所示,则?ABCD中,BC边上的高为
.
三.解答题
16.已知三角形一条边的长为xcm,这条边上的高为6cm,这个三角形的面积为ycm2.
(1)写出y与x的函数表达式;
(2)画出这个函数的图象.
17.求下列函数中自变量x的取值范围.
(1)y=﹣x;
(2)y=x+;
(3)y=;
(4)y=.
18.如表是某校高中毕业生升入高等学校人数比率的统计表:
年份
2003
2004
2005
2006
2007
2008
2009
2010
升学率
43.3%
49.9%
418.6%
46.1%
63.8%
73.2%
78.8%
83.5%
(1)其中有哪些变量?
(2)可以把其中的哪个变量看做另一个变量的函数?
参考答案
一.选择题
1.解:A、y=2x对于x的每一个取值,y都有唯一确定的值,符合函数的定义;
B、y=x2对于x的每一个取值,y都有唯一确定的值,符合函数的定义;
C、y=±
(x>0)对于x的每一个取值,y有两个确定的值,不符合函数的定义;
D、y=|x|对于x的每一个取值,y都有唯一确定的值,符合函数的定义.
故选:C.
2.解:由题意得,2﹣x≥0,
解得x≤2.
故选:B.
3.解:A、∵对于x的每一个取值,y都有唯一确定的值,故A正确;
B、∵对于x的每一个取值,y都有唯一确定的值,故B正确;
C、∵对于x的每一个取值,y都有唯一确定的值,故C正确;
D、∵对于x的每一个取值,y没有唯一确定的值,故D错误;
故选:D.
4.解:由题意,得
xy=15
常量为15,变量为x,y.
故选:A.
5.解:火车离A站的距离等于先行的3公理,加上后来t小时行驶的距离可得,
s=3+90t,
故选:A.
6.解:阿凯原本拿了4个蛋糕去结账,后来多买了一个50元的黑樱桃蛋糕,优惠方式为:价格最低的蛋糕免费.
①若原本四个蛋糕中最便宜的蛋糕价格等于50元或高于50元,最后买的黑樱桃蛋糕的最便宜的,免费,
∴此时原本结账金额等于后来结账的金额,即y=x;
②如果原本四个蛋糕中最便宜的蛋糕价格低于50元,则这个最便宜的蛋糕就变成免费,改以黑樱桃蛋糕计费,价格发生变化.
如果原本四个蛋糕中最便宜的是40元(伯爵茶蛋糕),买了黑樱桃蛋糕后,伯爵茶蛋糕变成免费,需要付黑樱桃蛋糕,多付10元,
此时,y=x+10;
③如果原本四个蛋糕中最便宜的是45元,买了黑樱桃蛋糕后,多付5元,
此时,y=x+5.
故选:D.
7.解:由图象可知,这一天中最高气温10°C,达到最高气温的时刻是16时.
故选:B.
8.解:根据题意可知:生产前没有积压代表图象从0开始,生产3小时后安排工人装箱每小时可装150件代表图象匀速上升到一定程度开始下匀速降为0.
故选:A.
9.解:相同的路程,甲用的时间短,那么甲的速度一定快.
故选:B.
10.解:根据题意和图形的形状,可知水的最大深度h与时间t之间的关系分为两段,先快后慢,
故选:D.
二.填空题
11.解:圆的半径发生变化时,面积也发生变化,圆面积S与半径r的关系为S=πr2,r是自变量,S是变量,π是常量.
故答案为:r,S,π.
12.解:由时间=路程÷速度可得,
t=,
故答案为:t=.
13.解:一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
故答案为:函数,自变量,因变量.
14.解:依题意有:y=2×5﹣2x=10﹣2x.
故答案为:y=10﹣2x.
15.解:观察图象可知;CD=4,AD=BC=8,设BC边上的高为h,
由题意:BC?h=24,
∴8h=24,
∴h=3,
故答案为:3.
三.解答题
16.解:(1)由题意,得:y==3x(x≥0);
(2)函数的图象如下所示:
17.解:(1)自变量的取值范围是全体实数;
(2)∵3x≠0,
∴x≠0;
(3)∵2x﹣1≠0,
∴x≠;
(4)∵x+4≠0,
∴x≠﹣4.
18.解:(1)由题可得变量为:年份和升学率;
(2)可以把其中的升学率看做年份的函数.
