北师大版数学2020-2021学年七年级下册4.3:探索三角形全等的条件 同步试题(word解析版)
文档属性
| 名称 | 北师大版数学2020-2021学年七年级下册4.3:探索三角形全等的条件 同步试题(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 807.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览


文档简介
北师大版数学2020-2021学年七年级下学期第四章4.3探索三角形全等的条件同步试题
一、单选题
1.下列结论正确的是( )
A.有两个锐角相等的两个直角三角形全等 B.一条斜边对应相等的两个直角三角形全等
C.两个等边三角形全等 D.有两边及其夹角对应相等的两个三角形全等
2.如图,点,,,在同一条直线上,点,在直线的两侧,,,添加下列哪个条件后,仍不能判定出( )
A. B. C. D.
3.如图,∠1=∠2,PC⊥OA于点C,PD⊥OB于D,则下列结论中错误的是( )
A.PC=PD B.OC=OD
C.∠OPC=∠OPD D.OA=OB
4.如图,,,,,则等于( )
A. B. C. D.
5.如图,测量河两岸相对的两点A,B的距离时,先在AB的垂线BF上取两点C,D,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△ABC的依据是( )
A.“边边边” B.“角边角”
C.“全等三角形定义” D.“边角边”
6.如图,①以点O为圆心,适当长为半径画弧,分别交OM、ON于A、C两点;②再分别以A,C为圆心,以大于AC长为半径画弧,两弧在∠MON内部交于点B;③作射线OB,则OB为∠MON的角平分线的依据为( )
A.SAS B.SSS C.HL D.ASA
7.如图,已知,,且,,,则的度数为( )
A. B. C. D.
8.如图,点,分别在线段,上,与相交于点,若,,则图中全等三角形的对数为( )
A.5对 B.4对 C.3对 D.2对
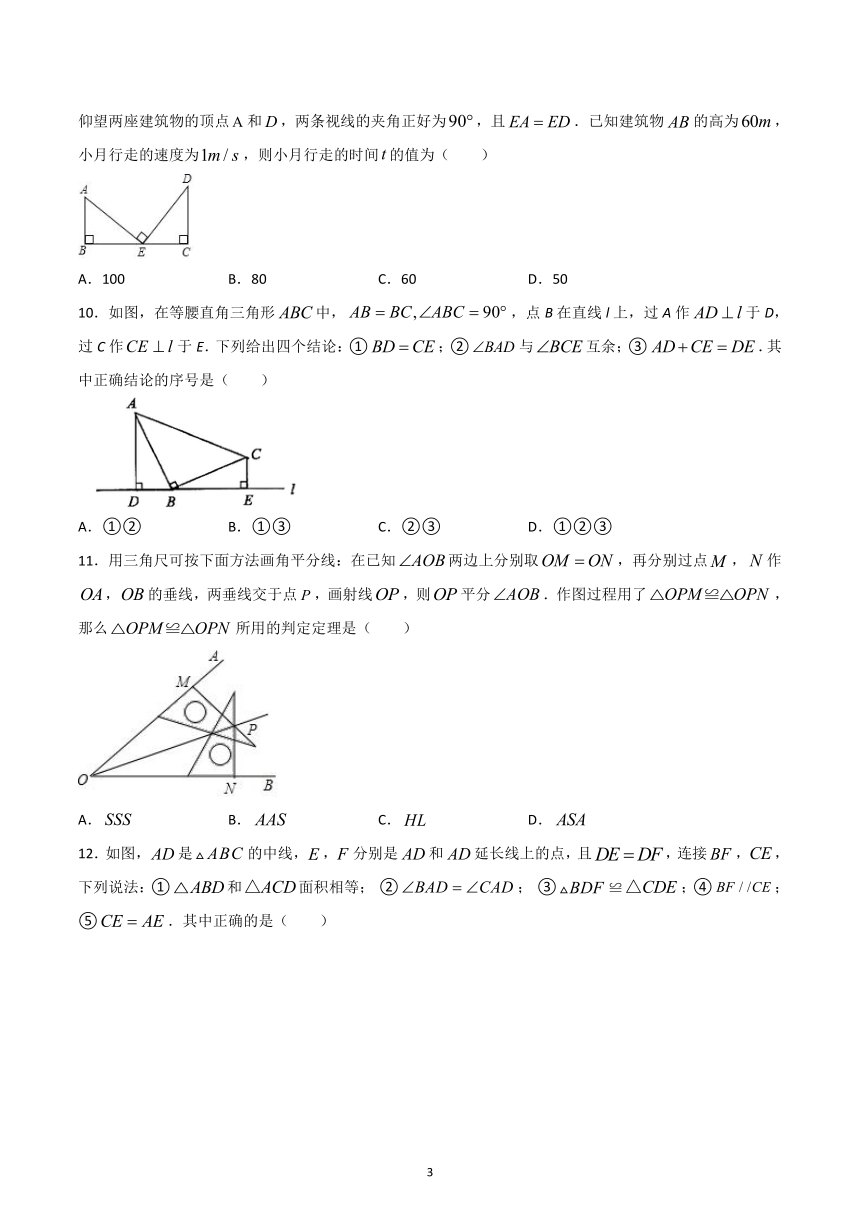
9.如图,两座建筑物,相距160km,小月从点沿BC走向点C,行走ts后她到达点,此时她仰望两座建筑物的顶点和,两条视线的夹角正好为,且.已知建筑物的高为,小月行走的速度为,则小月行走的时间的值为( )
A.100 B.80 C.60 D.50
10.如图,在等腰直角三角形中,,点B在直线l上,过A作于D,过C作于E.下列给出四个结论:①;②与互余;③.其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
11.用三角尺可按下面方法画角平分线:在已知两边上分别取,再分别过点,作,的垂线,两垂线交于点,画射线,则平分.作图过程用了,那么所用的判定定理是( )
A. B. C. D.
12.如图,是的中线,,分别是和延长线上的点,且,连接,,下列说法:①和面积相等; ②; ③≌;④;⑤.其中正确的是( )
A.①② B.①③
C.①③④ D.①④⑤
二、填空题
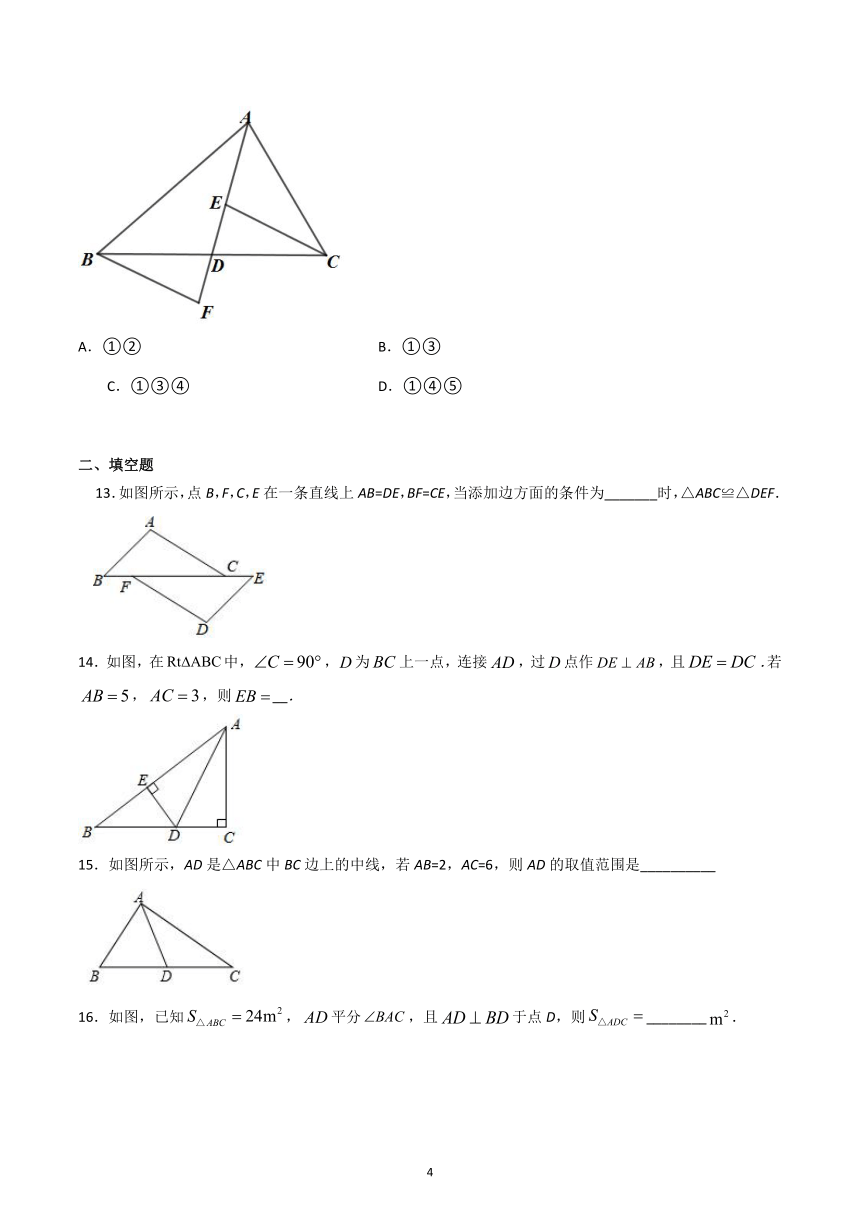
13.如图所示,点B,F,C,E在一条直线上AB=DE,BF=CE,当添加边方面的条件为_______时,△ABC≌△DEF.
14.如图,在中,,为上一点,连接,过点作,且.若,,则__.
15.如图所示,AD是△ABC中BC边上的中线,若AB=2,AC=6,则AD的取值范围是__________
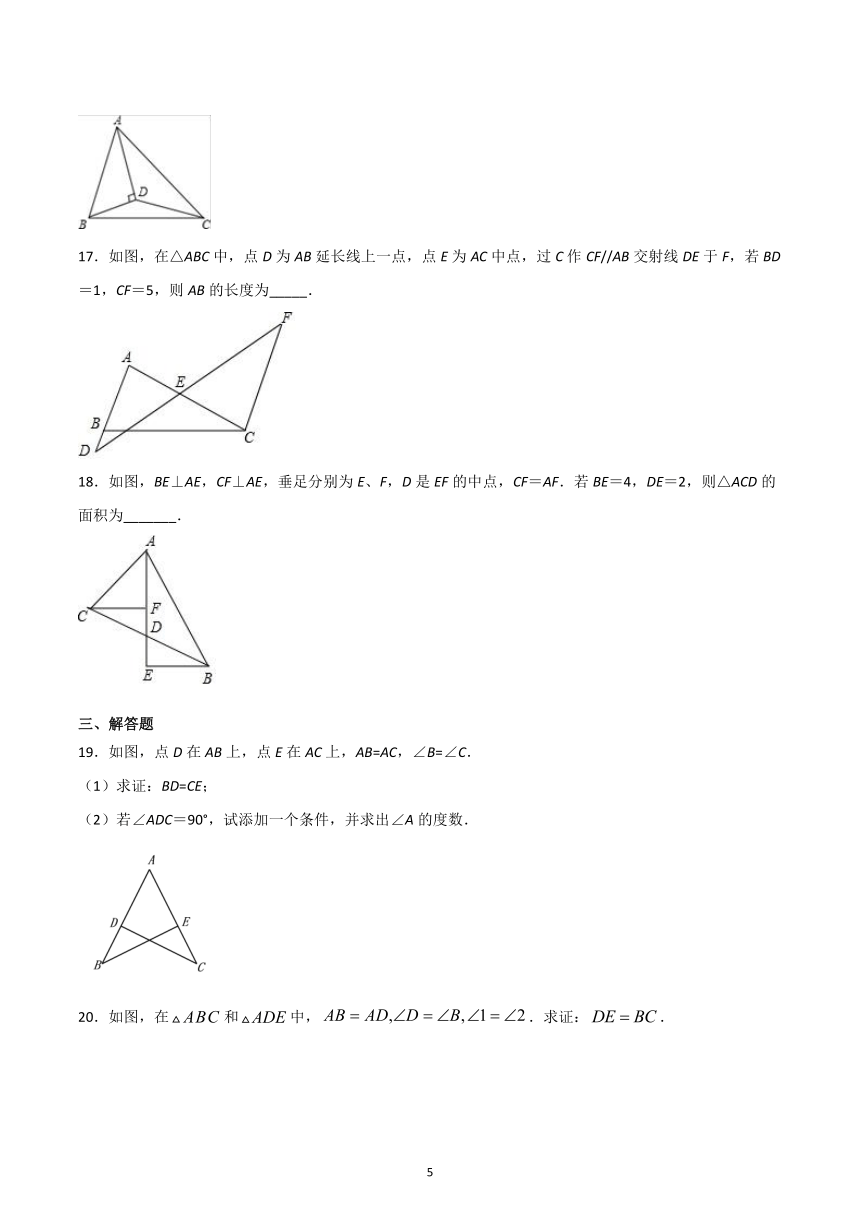
16.如图,已知,平分,且于点D,则________.
17.如图,在△ABC中,点D为AB延长线上一点,点E为AC中点,过C作CF//AB交射线DE于F,若BD=1,CF=5,则AB的长度为_____.
18.如图,BE⊥AE,CF⊥AE,垂足分别为E、F,D是EF的中点,CF=AF.若BE=4,DE=2,则△ACD的面积为_______.
三、解答题
19.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
(1)求证:BD=CE;
(2)若∠ADC=90°,试添加一个条件,并求出∠A的度数.
20.如图,在和中,.求证:.
21.如图,AD=AB,AE=AC,∠BAD=∠CAE.BE与CD交于点O.
求证:(1)BE=CD
(2)∠BOD=∠BAD
22.如图,小明和小华两家位于A,B两处,隔河相望.要测得两家之间的距离,小明设计如下方案:从点B出发沿河岸画一条射线BF,在BF上截取,过点D作,取点E使E,C,A在同一条直线上,则DE的长就是A,B之间的距离,说明他设计的道理.
23.如图,正方形的对角线、相交于点,、分别在、上,,求证:.
24.已知:在△ABC和△DBE中,AB=DB,BC=BE,其中∠ABD=∠CBE.
(1)如图1,求证:AC=DE;
(2)如图2,AB=BC,AC分别交DE,BD于点F,G,BC交DE于点H,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
25.如图1,已知AB=AC,AB⊥AC.直线m经过点A,过点B作BD⊥m于D, CE⊥m于E.我们把这种常见图形称为“K”字图.
(1)悟空同学对图1进行一番探究后,得出结论:DE=BD+CE,现请你替悟空同学完成证明过程.
(2)悟空同学进一步对类似图形进行探究,在图2中,若AB=AC,∠BAC=∠BDA=∠AEC,则结论DE=BD+CE,还成立吗?如果成立,请证明之.
参考答案
1.D
A、由于判断两个三角形全等,必须要一组边相等,所以有两个锐角相等的两个直角三角形全等的说法错误;
B、由于直角三角形除了直角,还需两个条件才能判断这两个直角三角形全等,所以一条斜边对应相等的两个直角三角形全等的说法错误;
C、由于判断两个三角形全等,必须要一组边相等,所以两个等边三角形全等的说法错误;
D、有两边及其夹角对应相等的两个三角形全等,说法正确.
故选:D.
2.A
解:,
,
,
,
即,
当添加,即时,可根据“”判断;
当添加时,可根据“”判断;
当添加时,可根据“”判断.
故选:.
3.D
【详解】
解:∵PC⊥OA于点C,PD⊥OB于D,
∴∠PCO=∠PDO=90°,
在△OPC和△OPD中,
∴△OPC≌△OPD(AAS),
∴PC=PD,OC=OD,∠COP=∠DOP,
∴A、B、C正确,
故选:D.
4.C
解:∵如图,在△AOD中,∠O=50°,∠D=30°,
∴∠OAD=180°-50°-30°=100°,
在△AOD与△BOC中,
∴△AOD≌△BOC(SAS),
故∠D=∠C=30°.
∴∠AEC=∠OAD-∠C=70°,
故选:C.
5.B
【详解】
解:由题意可得∠ABC=∠CDE=90°,
在△EDC和△ABC中,
∴△EDC≌△ABC(ASA),
故选:B.
6.B
【分析】
连接AB,BC,根据SSS证明三角形全等即可解决问题.
【详解】
解:如图,连接AB,BC,
在△BOA和△BOC中,
,
∴△BOA≌△BOC(SSS),
∴∠AOB=∠COB,
∴OB平分∠MON,
故选:B.
7.C
【详解】
在△ABC和△ADE中
∴ △ABC≌△ADE(SAS)
∴∠BAC=∠DAE
∵∠EAB=∠BAC+∠DAE+∠CAD=120°
∴∠BAC=∠DAE
∴∠BAF=∠BAC+∠CAD=65°
∴在△AFB中,∠AFB=180°-∠B-∠BAF=90°
∴∠GFD=90°
在△FGD中,∠EGF=∠D+∠GFD=115°
故选:C
8.B
【详解】
解:在△AOD和△BOC中
?OC=OD
∠AOD=∠BOC
∴△AOD≌△BOC(SAS)
∴OA=OB
∵OC=OD,OA=OB,
∴AC=BD,
在△ACE和△BDE中
∠A=∠B
∠AEC=∠BED
?AC=BD
∴△ACE≌△BDE(AAS),
∴AE=BE
∴AE=BE,
在△AOE和△BOE中
?OA=OB
∠A=∠B
?AE=BE
∴△AOE≌△BOE(SAS),
∴∠COE=∠DOE,
在△COE和△DOE中
?OC=OD
∠COE=∠DOE
?OE=OE
∴△COE≌△DOE(SAS),
故全等的三角形有4对.
故选:B.
9.A
【详解】
解:∵∠AED=90°,
∴∠AEB+∠DEC=90°,
∵∠ABE=90°,
∴∠A+∠AEB=90°,
∴∠A=∠DEC,
在△ABE和△DCE中
,
∴△ABE≌△ECD(AAS),
∴EC=AB=60m,
∵BC=160m,
∴BE=100m,
∴小华走的时间是100÷1=100(s),
故选:A.
10.D
证明:∵, ,
∴∠ADB=∠BEC=90°,
∴∠BAD+∠ABD=90°,∠BCE+∠CBE=90°,
∵,
∴∠ABD+∠CBE=90°,
∴∠BAD=∠CBE,
∴∠BCE+∠BAD=90°,故②正确;
∵∠BAD=∠CBE,∠ADB=∠BEC=90°,
∴△ADB≌△BEC,
∴,AD=BE,故①正确;
DE=DB+BE=CE+AD,故③正确;
11.C
【详解】
解:∵OM⊥MP,ON⊥NP,
∴∠OMP=∠ONP=90°,
在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL).
故选:C.
12.C
【详解】
解:∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,,
∴△BDF≌△CDE(SAS),故③正确;
∴∠F=∠DEC,
∴BF∥CE,故④正确;
∵△BDF≌△CDE,
∴CE=BF,故⑤错误,
正确的结论为:①③④,
故选:C.
13.AC=DF
【详解】
解:适合的条件是AC=DF,
∵BF=CE,
∴BF+FC=CE+FC,即BC=EF,
理由是:∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
故答案为:AC=DF.
14.2
解:∵,,
在和中,
,
,
,
,
故答案为2.
15.2<AD<4
【详解】
解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系定理:6-2<AE<6+2,
∴2<AD<4,
故AD的取值范围为2<AD<4.
16.12
【详解】
解:如图,延长BD交AC于点E,
∵平分,,
∴,.
∵,
∴.
∴.
∴,.
∴.
即.
∵,
∴.
故答案为:12.
17.4
【详解】
∵CF∥AB,
∴∠ADE=∠F,∠FCE=∠A.
∵点E为AC的中点,
∴AE=EC.
∵在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS).
∴AD=CF=5,
∵BD=1,
∴AB=AD-BD=5-1=4.
故答案为:4.
18.12
【详解】
解:∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD,
∵D是EF的中点,
∴ED=FD,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA).
∴CF=EB=4,
∵AF=CF,
∴AF=4,
∵D是EF的中点,
∴DF=DE=2,
∴AD=6,
∴△ACD的面积:.
故答案为:
19.【详解】
(1)证明:在△ADE和△FCE中,
∴△ACD≌△ABE,
∴AD=AE.
∴,即BD=CE.
(2)添加条件:∠C=40°,
∵∠ADC=90°,∠C=40°,
∴∠A=90°-40°=50°.
20.
证明:∵,
∴即,
在和中
∴,
∴.
21.
解:(1)证明:∵∠BAD=∠CAE
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB
在△ACD和△AEB中
∴△ACD≌△AEB
∴CD=BE
(2)由(1)可知∠ADC=∠ABE
又∵∠1=∠2
∠1+∠ADC+∠BAD=∠2+∠ABE+∠BOD=180°
∴∠BOD=∠BAD
22
解:,
,
在和中,
,
,
,
即的长就是、两点之间的距离.
23.
【详解】
证明:∵四边形ABCD为正方形,
∴OA=OB,AC⊥BD,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS)
∴AE=BF.
24
【详解】
证明:(1)∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
即∠ABC=∠DBE,
在△ABC与△DBE中,,
∴△ABC≌△DBE(SAS),
∴AC=DE;
(2)由(1)得△ABC≌△DBE,
∴∠A=∠D,∠C=∠E,AB=DB,BC=BE,
∴AB=BE,
∵AB=BC,
∴∠A=∠C,
∴∠A=∠E,
在△ABG与△EBH中,
∴△ABG≌△EBH(ASA),
∴BG=BH,
在△DBH与△CBG中,
∴△DBH≌△CBG(SAS),
∴∠D=∠C,
∵DB=CB,BG=BH,
∴DG=CF,
在△DFG与△CFH中,,
∴△DFG≌△CFH(AAS).
25.
证明:(1)∵AB⊥AC,BD⊥DE,CE⊥DE,
∴∠BDA=∠AEC=∠BAC=90°,
∴∠DAB+∠ABD=∠EAC+∠DAB=90°,
∴∠ABD=∠EAC,
在△ABD和 △CAE中,
,
∴ △ABD ≌ △CAE(AAS),
∴ BD = AE ,AD = CE,
∴ DE = AE + DA ;
(2)成立,
理由如下:∵ ∠BAC + ∠BAD + ∠EAC = 180° ,
∠ADB+ ∠BAD + ∠ABD = 180°,
∠BAC = ∠BDA,
∴∠ABD = ∠EAC ,
在△ABD和 △CAE中,
,
∴ △ABD ≌ △CAE(AAS),
∴ BD = AE,AD = CE,
∴ DE = AE + DA = BD + CE.
一、单选题
1.下列结论正确的是( )
A.有两个锐角相等的两个直角三角形全等 B.一条斜边对应相等的两个直角三角形全等
C.两个等边三角形全等 D.有两边及其夹角对应相等的两个三角形全等
2.如图,点,,,在同一条直线上,点,在直线的两侧,,,添加下列哪个条件后,仍不能判定出( )
A. B. C. D.
3.如图,∠1=∠2,PC⊥OA于点C,PD⊥OB于D,则下列结论中错误的是( )
A.PC=PD B.OC=OD
C.∠OPC=∠OPD D.OA=OB
4.如图,,,,,则等于( )
A. B. C. D.
5.如图,测量河两岸相对的两点A,B的距离时,先在AB的垂线BF上取两点C,D,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△ABC的依据是( )
A.“边边边” B.“角边角”
C.“全等三角形定义” D.“边角边”
6.如图,①以点O为圆心,适当长为半径画弧,分别交OM、ON于A、C两点;②再分别以A,C为圆心,以大于AC长为半径画弧,两弧在∠MON内部交于点B;③作射线OB,则OB为∠MON的角平分线的依据为( )
A.SAS B.SSS C.HL D.ASA
7.如图,已知,,且,,,则的度数为( )
A. B. C. D.
8.如图,点,分别在线段,上,与相交于点,若,,则图中全等三角形的对数为( )
A.5对 B.4对 C.3对 D.2对
9.如图,两座建筑物,相距160km,小月从点沿BC走向点C,行走ts后她到达点,此时她仰望两座建筑物的顶点和,两条视线的夹角正好为,且.已知建筑物的高为,小月行走的速度为,则小月行走的时间的值为( )
A.100 B.80 C.60 D.50
10.如图,在等腰直角三角形中,,点B在直线l上,过A作于D,过C作于E.下列给出四个结论:①;②与互余;③.其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
11.用三角尺可按下面方法画角平分线:在已知两边上分别取,再分别过点,作,的垂线,两垂线交于点,画射线,则平分.作图过程用了,那么所用的判定定理是( )
A. B. C. D.
12.如图,是的中线,,分别是和延长线上的点,且,连接,,下列说法:①和面积相等; ②; ③≌;④;⑤.其中正确的是( )
A.①② B.①③
C.①③④ D.①④⑤
二、填空题
13.如图所示,点B,F,C,E在一条直线上AB=DE,BF=CE,当添加边方面的条件为_______时,△ABC≌△DEF.
14.如图,在中,,为上一点,连接,过点作,且.若,,则__.
15.如图所示,AD是△ABC中BC边上的中线,若AB=2,AC=6,则AD的取值范围是__________
16.如图,已知,平分,且于点D,则________.
17.如图,在△ABC中,点D为AB延长线上一点,点E为AC中点,过C作CF//AB交射线DE于F,若BD=1,CF=5,则AB的长度为_____.
18.如图,BE⊥AE,CF⊥AE,垂足分别为E、F,D是EF的中点,CF=AF.若BE=4,DE=2,则△ACD的面积为_______.
三、解答题
19.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
(1)求证:BD=CE;
(2)若∠ADC=90°,试添加一个条件,并求出∠A的度数.
20.如图,在和中,.求证:.
21.如图,AD=AB,AE=AC,∠BAD=∠CAE.BE与CD交于点O.
求证:(1)BE=CD
(2)∠BOD=∠BAD
22.如图,小明和小华两家位于A,B两处,隔河相望.要测得两家之间的距离,小明设计如下方案:从点B出发沿河岸画一条射线BF,在BF上截取,过点D作,取点E使E,C,A在同一条直线上,则DE的长就是A,B之间的距离,说明他设计的道理.
23.如图,正方形的对角线、相交于点,、分别在、上,,求证:.
24.已知:在△ABC和△DBE中,AB=DB,BC=BE,其中∠ABD=∠CBE.
(1)如图1,求证:AC=DE;
(2)如图2,AB=BC,AC分别交DE,BD于点F,G,BC交DE于点H,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
25.如图1,已知AB=AC,AB⊥AC.直线m经过点A,过点B作BD⊥m于D, CE⊥m于E.我们把这种常见图形称为“K”字图.
(1)悟空同学对图1进行一番探究后,得出结论:DE=BD+CE,现请你替悟空同学完成证明过程.
(2)悟空同学进一步对类似图形进行探究,在图2中,若AB=AC,∠BAC=∠BDA=∠AEC,则结论DE=BD+CE,还成立吗?如果成立,请证明之.
参考答案
1.D
A、由于判断两个三角形全等,必须要一组边相等,所以有两个锐角相等的两个直角三角形全等的说法错误;
B、由于直角三角形除了直角,还需两个条件才能判断这两个直角三角形全等,所以一条斜边对应相等的两个直角三角形全等的说法错误;
C、由于判断两个三角形全等,必须要一组边相等,所以两个等边三角形全等的说法错误;
D、有两边及其夹角对应相等的两个三角形全等,说法正确.
故选:D.
2.A
解:,
,
,
,
即,
当添加,即时,可根据“”判断;
当添加时,可根据“”判断;
当添加时,可根据“”判断.
故选:.
3.D
【详解】
解:∵PC⊥OA于点C,PD⊥OB于D,
∴∠PCO=∠PDO=90°,
在△OPC和△OPD中,
∴△OPC≌△OPD(AAS),
∴PC=PD,OC=OD,∠COP=∠DOP,
∴A、B、C正确,
故选:D.
4.C
解:∵如图,在△AOD中,∠O=50°,∠D=30°,
∴∠OAD=180°-50°-30°=100°,
在△AOD与△BOC中,
∴△AOD≌△BOC(SAS),
故∠D=∠C=30°.
∴∠AEC=∠OAD-∠C=70°,
故选:C.
5.B
【详解】
解:由题意可得∠ABC=∠CDE=90°,
在△EDC和△ABC中,
∴△EDC≌△ABC(ASA),
故选:B.
6.B
【分析】
连接AB,BC,根据SSS证明三角形全等即可解决问题.
【详解】
解:如图,连接AB,BC,
在△BOA和△BOC中,
,
∴△BOA≌△BOC(SSS),
∴∠AOB=∠COB,
∴OB平分∠MON,
故选:B.
7.C
【详解】
在△ABC和△ADE中
∴ △ABC≌△ADE(SAS)
∴∠BAC=∠DAE
∵∠EAB=∠BAC+∠DAE+∠CAD=120°
∴∠BAC=∠DAE
∴∠BAF=∠BAC+∠CAD=65°
∴在△AFB中,∠AFB=180°-∠B-∠BAF=90°
∴∠GFD=90°
在△FGD中,∠EGF=∠D+∠GFD=115°
故选:C
8.B
【详解】
解:在△AOD和△BOC中
?OC=OD
∠AOD=∠BOC
∴△AOD≌△BOC(SAS)
∴OA=OB
∵OC=OD,OA=OB,
∴AC=BD,
在△ACE和△BDE中
∠A=∠B
∠AEC=∠BED
?AC=BD
∴△ACE≌△BDE(AAS),
∴AE=BE
∴AE=BE,
在△AOE和△BOE中
?OA=OB
∠A=∠B
?AE=BE
∴△AOE≌△BOE(SAS),
∴∠COE=∠DOE,
在△COE和△DOE中
?OC=OD
∠COE=∠DOE
?OE=OE
∴△COE≌△DOE(SAS),
故全等的三角形有4对.
故选:B.
9.A
【详解】
解:∵∠AED=90°,
∴∠AEB+∠DEC=90°,
∵∠ABE=90°,
∴∠A+∠AEB=90°,
∴∠A=∠DEC,
在△ABE和△DCE中
,
∴△ABE≌△ECD(AAS),
∴EC=AB=60m,
∵BC=160m,
∴BE=100m,
∴小华走的时间是100÷1=100(s),
故选:A.
10.D
证明:∵, ,
∴∠ADB=∠BEC=90°,
∴∠BAD+∠ABD=90°,∠BCE+∠CBE=90°,
∵,
∴∠ABD+∠CBE=90°,
∴∠BAD=∠CBE,
∴∠BCE+∠BAD=90°,故②正确;
∵∠BAD=∠CBE,∠ADB=∠BEC=90°,
∴△ADB≌△BEC,
∴,AD=BE,故①正确;
DE=DB+BE=CE+AD,故③正确;
11.C
【详解】
解:∵OM⊥MP,ON⊥NP,
∴∠OMP=∠ONP=90°,
在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL).
故选:C.
12.C
【详解】
解:∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,,
∴△BDF≌△CDE(SAS),故③正确;
∴∠F=∠DEC,
∴BF∥CE,故④正确;
∵△BDF≌△CDE,
∴CE=BF,故⑤错误,
正确的结论为:①③④,
故选:C.
13.AC=DF
【详解】
解:适合的条件是AC=DF,
∵BF=CE,
∴BF+FC=CE+FC,即BC=EF,
理由是:∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
故答案为:AC=DF.
14.2
解:∵,,
在和中,
,
,
,
,
故答案为2.
15.2<AD<4
【详解】
解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系定理:6-2<AE<6+2,
∴2<AD<4,
故AD的取值范围为2<AD<4.
16.12
【详解】
解:如图,延长BD交AC于点E,
∵平分,,
∴,.
∵,
∴.
∴.
∴,.
∴.
即.
∵,
∴.
故答案为:12.
17.4
【详解】
∵CF∥AB,
∴∠ADE=∠F,∠FCE=∠A.
∵点E为AC的中点,
∴AE=EC.
∵在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS).
∴AD=CF=5,
∵BD=1,
∴AB=AD-BD=5-1=4.
故答案为:4.
18.12
【详解】
解:∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD,
∵D是EF的中点,
∴ED=FD,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA).
∴CF=EB=4,
∵AF=CF,
∴AF=4,
∵D是EF的中点,
∴DF=DE=2,
∴AD=6,
∴△ACD的面积:.
故答案为:
19.【详解】
(1)证明:在△ADE和△FCE中,
∴△ACD≌△ABE,
∴AD=AE.
∴,即BD=CE.
(2)添加条件:∠C=40°,
∵∠ADC=90°,∠C=40°,
∴∠A=90°-40°=50°.
20.
证明:∵,
∴即,
在和中
∴,
∴.
21.
解:(1)证明:∵∠BAD=∠CAE
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB
在△ACD和△AEB中
∴△ACD≌△AEB
∴CD=BE
(2)由(1)可知∠ADC=∠ABE
又∵∠1=∠2
∠1+∠ADC+∠BAD=∠2+∠ABE+∠BOD=180°
∴∠BOD=∠BAD
22
解:,
,
在和中,
,
,
,
即的长就是、两点之间的距离.
23.
【详解】
证明:∵四边形ABCD为正方形,
∴OA=OB,AC⊥BD,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS)
∴AE=BF.
24
【详解】
证明:(1)∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
即∠ABC=∠DBE,
在△ABC与△DBE中,,
∴△ABC≌△DBE(SAS),
∴AC=DE;
(2)由(1)得△ABC≌△DBE,
∴∠A=∠D,∠C=∠E,AB=DB,BC=BE,
∴AB=BE,
∵AB=BC,
∴∠A=∠C,
∴∠A=∠E,
在△ABG与△EBH中,
∴△ABG≌△EBH(ASA),
∴BG=BH,
在△DBH与△CBG中,
∴△DBH≌△CBG(SAS),
∴∠D=∠C,
∵DB=CB,BG=BH,
∴DG=CF,
在△DFG与△CFH中,,
∴△DFG≌△CFH(AAS).
25.
证明:(1)∵AB⊥AC,BD⊥DE,CE⊥DE,
∴∠BDA=∠AEC=∠BAC=90°,
∴∠DAB+∠ABD=∠EAC+∠DAB=90°,
∴∠ABD=∠EAC,
在△ABD和 △CAE中,
,
∴ △ABD ≌ △CAE(AAS),
∴ BD = AE ,AD = CE,
∴ DE = AE + DA ;
(2)成立,
理由如下:∵ ∠BAC + ∠BAD + ∠EAC = 180° ,
∠ADB+ ∠BAD + ∠ABD = 180°,
∠BAC = ∠BDA,
∴∠ABD = ∠EAC ,
在△ABD和 △CAE中,
,
∴ △ABD ≌ △CAE(AAS),
∴ BD = AE,AD = CE,
∴ DE = AE + DA = BD + CE.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
