分式的概念学案
图片预览




文档简介
《分式的概念》学案
一、知识梳理:
1、_________________________________________叫分式。当________________时,分式有意义;当_________________时,分式无意义;当__________________时,分式值为零;当______________时,分式值为1。
2、_____________和____________________统称为有理式。
二、课堂精练:
1、下列各式:① ② ③ ④ ⑤ ⑥,其中整式有__________________,分式有________________,有理式有____________________________。
2、下列分式中,一定有意义的是_____________
A、 B、 C、 D、
3、题2中错误的选项要有意义,请你求各式的x的取值范围。
4、要使分式的值为零,则x的取值是____________________。
5、当________________时,分式无意义。
6、对于分式,当___________时,它的值为正;当______________时,它的值为负。
三、双基巩固:
1、请你写出一个分式,满足当x=2时它无意义,这个分式可以是__________________;当x=2时它的值为零,这个分式可以是______________________。
2、当x_______________时,分式无意义。
3、若分式的值为零,则x=____________________。
4、当x=-2时,分式无意义,当x=4时,分式值为零,则a+b=__________________。
5、在① ② ③ ④中,值可能为零的有___________________。
6、当_________________时,分式有意义;当___________________时,分式的值为零。
7、已知x=2时,分式无意义,那么x为何值时,它的值为零。
8、若分式的值为正整数,求整数m的值。
《分式的基本性质》学案(一)
一、知识梳理:
1、分式的基本性质:_____________________________________________________________。
2、用数学语言表示分式的基本性质:
____________________________________________________________________
3、分子与分母_______________________的分式称为最简分式。
二、课堂精练:
1、判断下列变形是否正确。
①若c≠0,则 ( ) ② ( )
③ ( ) ④ ( )
⑤ ( ) ⑥ ( )
2、利用分式的基本性质填空:
① ② ③
3、不改变分式的值,把分式中分子、分母各项系数化为整数,结果为____________。
4、下列分式:① ② ③ ④ ⑤ 中,是最简分式的有__________________。
5、分式的约分是把一个分式分子与分母的__________________约去。
6、公因式的系数是___________________________,然后取相同字母或因式的____________。
三、双基巩固:
1、把分式中的x、y都扩大到原来的2倍,则分式的值___________________。
2、不改变分式的值,使下列分式的分子、分母的最高次项系数为正数。
=___________________, =_________________________
=______________________。
3、在下列的括号内填上适当的“+”、“-”号,使等式成立。
4、当_______________时,分式
5、化简下列分式:
① ② ③
④ ⑤ ⑥
⑦ ⑧
《分式的基本性质》学案(二)
一、知识梳理:
1、分式的通分是________________________________________________________________。通分的关键是确定几个分式的分母的__________________________。
2、确定最简公分母的方法:①找各个分母的系数的_____________________作为最简公分母的系数②找各个分母所含字母或因式的______________________________作为最简公分母的字母或因式。
3、通分的依据是_________________________________________。
二、课堂精练:
1、分式,,的最简公分母是______________________,它们通分后分别为____________、_______________、___________________。
2、分式,,的最简公分母是______________________,它们通分后分别为__________________,_______________________,____________________。
3、分式,,的最简公分母是____________________,它们通分后分别是________________,____________________,________________________。
4、通分:
(1), (2),
三、双基巩固:
1、通分:
(1), (2),,
(3)
(4)
2、已知a-b-3ab=0,求分式的值.
3、若,求分式的值。
《分式的乘除法》学案
一、知识梳理:
分式乘以分式,用______________作为积的分子,__________________作为积的分母;分式除以分式,把_______________________________后,与被除式相乘,分式的乘方要把分子、分母分别_____________________。
二、巩固练习:
1、选择题:
(1)、下列各式计算正确的是( )
A. B.
C. D.
(2)、计算的结果是( )
A.a2 B. C. D.
(3)、如果从一捆均匀的电线上取1m长的电线,称得其质量为 a,再称得剩余的质量为b,那么原来这捆电线的总长度是( )m
A. B. C. D.
2、填空:
(1)、计算:___________________________
(2)、计算:_________________________
(3)、若
(4)、:,则a:b:c=________________________
3、解答题:
(1) (2)
(3) (4)
(5) (6)
(7) (8)
三、拓展与探究:
1、一次数学课堂上,李老师给大家出了这样一道题目:
当x分别为3,,时,求代数式的值。小明一看,太复杂了,怎么算呢?你能帮小明解决这个问题吗?请写出具体的解题过程。
2、已知:3x+2y=13,2x-3y=0.求下面式子:
的值。
3、化简,求值:,其中。
《分式的加减法》学案
一、知识梳理:
同分母分式相加减,分母___________,把分子________________________;异分母分式相加减,先________________,变成同分母分式,再加减。分式的混合运算应先算____________,再算___________________,最后算______________________,如果有括号,先算括号内的。
二、课堂精练:
1、计算的结果是( )
A.-1 B.0 C.2 D.1
2、计算的结果是( )
A. B.a-3 C. D.
3、化简的结果是( )
A. B. C. D.
4、计算的结果是___________________。
5、若,则M=________________________。
6、化简_______________________。
7、若________________________。
三、双基巩固:
计算:
1、 2、
3、 4、
5、 6、
四、拓展探究:
1、已知x为整数,且为整数,求所有符合条件的x的值的和.
2、对于正数x,规定,例如,计算:
+…+__________________________。
3、先化简,再在0、1、2、3中选一个你认为合适的a的值,代入求值。
《分式方程》学案(一)
一、知识梳理:
分母中含有________________的方程叫做分式方程,解分式方程的步骤是:①___________________②___________________________③___________________________④__________________________。
将分式方程变形为整式方程时,有可能产生不适合原方程的根,这种根通常称为__________________。
二、巩固与练习:
1、下列方程不是分式方程的是( )
A. B. C. D.
2、若分式方程有增根,则a的值是( )
A 4 B 2 C 1 D 0
3、方程的解是________________
4、当x=__________时,2x-3与的值互为倒数。
5、当k=____________时,分式方程有增根.
6、若关于x的方程有唯一解,则a、b应满足的条件是________________。
7、解方程:
(1) (2)
(3) (4)
三、拓展探究:
1、已知,求A、B的值。
2、当x为何值时,的值与的值互为相反数?
《分式方程的应用》学案(二)
一、知识梳理:
列分式方程解应用题的一般步骤:①_____________________②_________________③____________④__________________⑤_______________________________⑥_______________________。
二、巩固与练习:
1、某煤厂原计划x天生产120吨煤,由于采用了新技术,每天增产3吨,因此提前2天完成了任务。列方程为( )
A. B.
C. D.
2、沿河两地相距S㎞,船在静水中的速度是a㎞/h,水流速度为b㎞/h,此船往返一次所需的时间为( )h.
A. B. C. D.
3、赵强同学借了一本书,共280页,要在两周借读期内读完,当他读了一半时,发现以后平均每天要多读21页才能在借读期内读完,他读前一半时,平均每天读多少页?如果设他读前一半时,平均每天读x页,则下列方程正确的是( )
A. B.
C. D.
4、若有m人,a天内可完成某项工程,则(m+r)人完成此项工程所需天数为_____________
5、一条路全长m千米,骑自行车b小时能到达,为了提前1小时到达,自行车每小时应该多走___________千米。
6、A、B两地相距135千米,两辆汽车从A地开往B地,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟,已知小汽车与大汽车的速度之比为5:2,求两车的速度。
7、有一项工程要在规定日期内完成,如果甲工程队单独做正好如期完成,如果乙工程队单独做则需要超过4天才能完成,现由甲、乙两队合做3天后,余下的工作由乙队单独完成,正如如期完成整个工程。则规定日期是多少天
《零指数幂和负指数幂、科学计数法》学案
一、知识梳理:
任何不等于0的数的零次幂都等于________,即a0=_______________(其中a____________);任何不等于零的数的-n次幂等于这个数的n次幂的___________或者等于这个数的__________的n次幂,即__________________________________(其中a________________,n为___________________)
二、巩固练习:
1、的值是( )
A. B.4 C. D.-4
2、下列计算正确的是( )
A. B.
C. D.
3、已知,则等于( )
A.4 B.2 C.6 D.8
4、0.000976用科学计数法表示为( )
A.0.976×10-3 B.9.76×10-3 C. 9.76×10-4 D. 9.76×10-6
5、长方形的长是3.2×103厘米,宽是2.5×102厘米,则它的面积是( )
A.8×106 B. 8×104 C. 8×105 D. 8×107
6、用小数表示-3×10-3,结果是( )
A.-0.03 B.-0.003 C.-0.0003 D.-0.3
7、用科学计数法表示下列各数:①0.0000304=________________②-0.000000305=_________________③人体大约有2万5千亿个红细胞,2万5千亿=______________________④北京故宫博物馆占地面积约为72000=____________________
8、成立的条件是__________________
9、若,则k的值是__________________________
10、若,则x的值是________________________
11、若5x-3y-2=0,则_____________________
三、拓展探究:
1、计算,使结果只含有正整指数幂
① ②
2、若,试比较的大小。
一、知识梳理:
1、_________________________________________叫分式。当________________时,分式有意义;当_________________时,分式无意义;当__________________时,分式值为零;当______________时,分式值为1。
2、_____________和____________________统称为有理式。
二、课堂精练:
1、下列各式:① ② ③ ④ ⑤ ⑥,其中整式有__________________,分式有________________,有理式有____________________________。
2、下列分式中,一定有意义的是_____________
A、 B、 C、 D、
3、题2中错误的选项要有意义,请你求各式的x的取值范围。
4、要使分式的值为零,则x的取值是____________________。
5、当________________时,分式无意义。
6、对于分式,当___________时,它的值为正;当______________时,它的值为负。
三、双基巩固:
1、请你写出一个分式,满足当x=2时它无意义,这个分式可以是__________________;当x=2时它的值为零,这个分式可以是______________________。
2、当x_______________时,分式无意义。
3、若分式的值为零,则x=____________________。
4、当x=-2时,分式无意义,当x=4时,分式值为零,则a+b=__________________。
5、在① ② ③ ④中,值可能为零的有___________________。
6、当_________________时,分式有意义;当___________________时,分式的值为零。
7、已知x=2时,分式无意义,那么x为何值时,它的值为零。
8、若分式的值为正整数,求整数m的值。
《分式的基本性质》学案(一)
一、知识梳理:
1、分式的基本性质:_____________________________________________________________。
2、用数学语言表示分式的基本性质:
____________________________________________________________________
3、分子与分母_______________________的分式称为最简分式。
二、课堂精练:
1、判断下列变形是否正确。
①若c≠0,则 ( ) ② ( )
③ ( ) ④ ( )
⑤ ( ) ⑥ ( )
2、利用分式的基本性质填空:
① ② ③
3、不改变分式的值,把分式中分子、分母各项系数化为整数,结果为____________。
4、下列分式:① ② ③ ④ ⑤ 中,是最简分式的有__________________。
5、分式的约分是把一个分式分子与分母的__________________约去。
6、公因式的系数是___________________________,然后取相同字母或因式的____________。
三、双基巩固:
1、把分式中的x、y都扩大到原来的2倍,则分式的值___________________。
2、不改变分式的值,使下列分式的分子、分母的最高次项系数为正数。
=___________________, =_________________________
=______________________。
3、在下列的括号内填上适当的“+”、“-”号,使等式成立。
4、当_______________时,分式
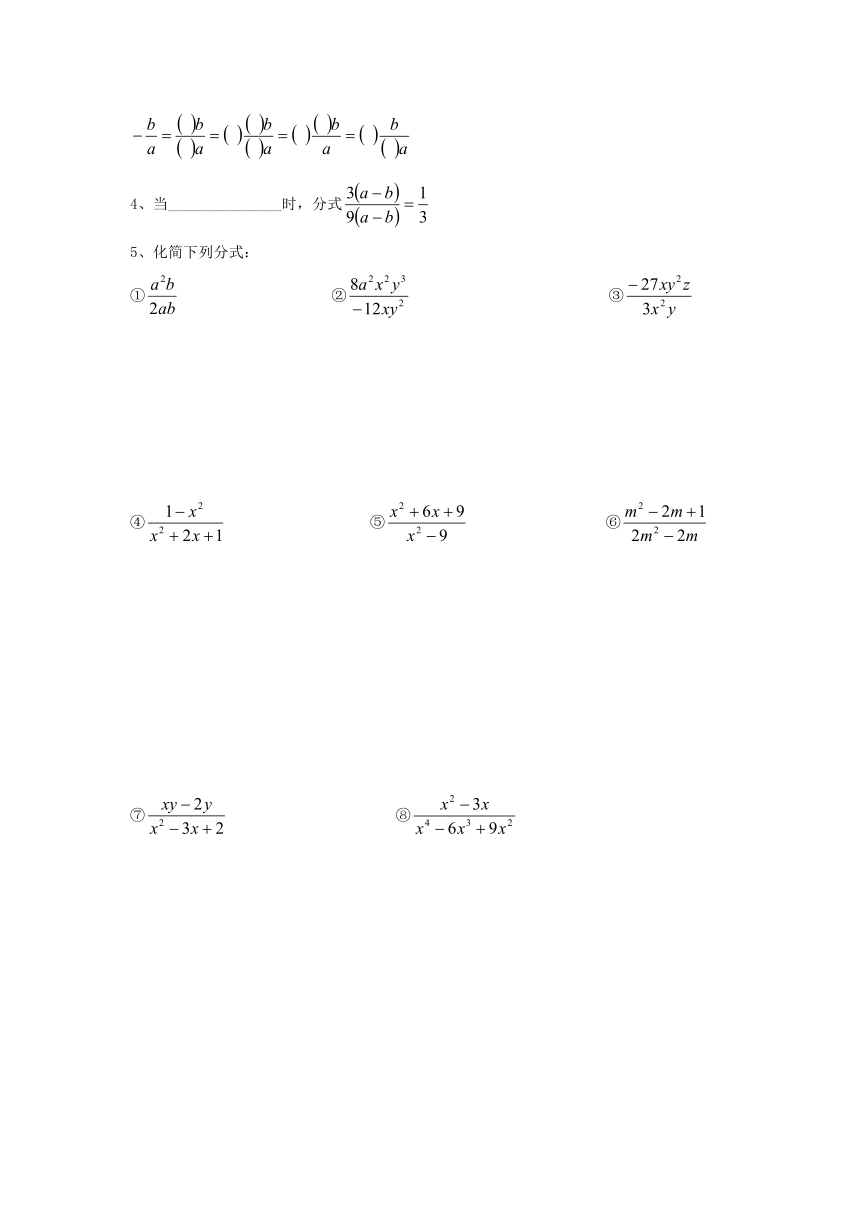
5、化简下列分式:
① ② ③
④ ⑤ ⑥
⑦ ⑧
《分式的基本性质》学案(二)
一、知识梳理:
1、分式的通分是________________________________________________________________。通分的关键是确定几个分式的分母的__________________________。
2、确定最简公分母的方法:①找各个分母的系数的_____________________作为最简公分母的系数②找各个分母所含字母或因式的______________________________作为最简公分母的字母或因式。
3、通分的依据是_________________________________________。
二、课堂精练:
1、分式,,的最简公分母是______________________,它们通分后分别为____________、_______________、___________________。
2、分式,,的最简公分母是______________________,它们通分后分别为__________________,_______________________,____________________。
3、分式,,的最简公分母是____________________,它们通分后分别是________________,____________________,________________________。
4、通分:
(1), (2),
三、双基巩固:
1、通分:
(1), (2),,
(3)
(4)
2、已知a-b-3ab=0,求分式的值.
3、若,求分式的值。
《分式的乘除法》学案
一、知识梳理:
分式乘以分式,用______________作为积的分子,__________________作为积的分母;分式除以分式,把_______________________________后,与被除式相乘,分式的乘方要把分子、分母分别_____________________。
二、巩固练习:
1、选择题:
(1)、下列各式计算正确的是( )
A. B.
C. D.
(2)、计算的结果是( )
A.a2 B. C. D.
(3)、如果从一捆均匀的电线上取1m长的电线,称得其质量为 a,再称得剩余的质量为b,那么原来这捆电线的总长度是( )m
A. B. C. D.
2、填空:
(1)、计算:___________________________
(2)、计算:_________________________
(3)、若
(4)、:,则a:b:c=________________________
3、解答题:
(1) (2)
(3) (4)
(5) (6)
(7) (8)
三、拓展与探究:
1、一次数学课堂上,李老师给大家出了这样一道题目:
当x分别为3,,时,求代数式的值。小明一看,太复杂了,怎么算呢?你能帮小明解决这个问题吗?请写出具体的解题过程。
2、已知:3x+2y=13,2x-3y=0.求下面式子:
的值。
3、化简,求值:,其中。
《分式的加减法》学案
一、知识梳理:
同分母分式相加减,分母___________,把分子________________________;异分母分式相加减,先________________,变成同分母分式,再加减。分式的混合运算应先算____________,再算___________________,最后算______________________,如果有括号,先算括号内的。
二、课堂精练:
1、计算的结果是( )
A.-1 B.0 C.2 D.1
2、计算的结果是( )
A. B.a-3 C. D.
3、化简的结果是( )
A. B. C. D.
4、计算的结果是___________________。
5、若,则M=________________________。
6、化简_______________________。
7、若________________________。
三、双基巩固:
计算:
1、 2、
3、 4、
5、 6、
四、拓展探究:
1、已知x为整数,且为整数,求所有符合条件的x的值的和.
2、对于正数x,规定,例如,计算:
+…+__________________________。
3、先化简,再在0、1、2、3中选一个你认为合适的a的值,代入求值。
《分式方程》学案(一)
一、知识梳理:
分母中含有________________的方程叫做分式方程,解分式方程的步骤是:①___________________②___________________________③___________________________④__________________________。
将分式方程变形为整式方程时,有可能产生不适合原方程的根,这种根通常称为__________________。
二、巩固与练习:
1、下列方程不是分式方程的是( )
A. B. C. D.
2、若分式方程有增根,则a的值是( )
A 4 B 2 C 1 D 0
3、方程的解是________________
4、当x=__________时,2x-3与的值互为倒数。
5、当k=____________时,分式方程有增根.
6、若关于x的方程有唯一解,则a、b应满足的条件是________________。
7、解方程:
(1) (2)
(3) (4)
三、拓展探究:
1、已知,求A、B的值。
2、当x为何值时,的值与的值互为相反数?
《分式方程的应用》学案(二)
一、知识梳理:
列分式方程解应用题的一般步骤:①_____________________②_________________③____________④__________________⑤_______________________________⑥_______________________。
二、巩固与练习:
1、某煤厂原计划x天生产120吨煤,由于采用了新技术,每天增产3吨,因此提前2天完成了任务。列方程为( )
A. B.
C. D.
2、沿河两地相距S㎞,船在静水中的速度是a㎞/h,水流速度为b㎞/h,此船往返一次所需的时间为( )h.
A. B. C. D.
3、赵强同学借了一本书,共280页,要在两周借读期内读完,当他读了一半时,发现以后平均每天要多读21页才能在借读期内读完,他读前一半时,平均每天读多少页?如果设他读前一半时,平均每天读x页,则下列方程正确的是( )
A. B.
C. D.
4、若有m人,a天内可完成某项工程,则(m+r)人完成此项工程所需天数为_____________
5、一条路全长m千米,骑自行车b小时能到达,为了提前1小时到达,自行车每小时应该多走___________千米。
6、A、B两地相距135千米,两辆汽车从A地开往B地,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟,已知小汽车与大汽车的速度之比为5:2,求两车的速度。
7、有一项工程要在规定日期内完成,如果甲工程队单独做正好如期完成,如果乙工程队单独做则需要超过4天才能完成,现由甲、乙两队合做3天后,余下的工作由乙队单独完成,正如如期完成整个工程。则规定日期是多少天
《零指数幂和负指数幂、科学计数法》学案
一、知识梳理:
任何不等于0的数的零次幂都等于________,即a0=_______________(其中a____________);任何不等于零的数的-n次幂等于这个数的n次幂的___________或者等于这个数的__________的n次幂,即__________________________________(其中a________________,n为___________________)
二、巩固练习:
1、的值是( )
A. B.4 C. D.-4
2、下列计算正确的是( )
A. B.
C. D.
3、已知,则等于( )
A.4 B.2 C.6 D.8
4、0.000976用科学计数法表示为( )
A.0.976×10-3 B.9.76×10-3 C. 9.76×10-4 D. 9.76×10-6
5、长方形的长是3.2×103厘米,宽是2.5×102厘米,则它的面积是( )
A.8×106 B. 8×104 C. 8×105 D. 8×107
6、用小数表示-3×10-3,结果是( )
A.-0.03 B.-0.003 C.-0.0003 D.-0.3
7、用科学计数法表示下列各数:①0.0000304=________________②-0.000000305=_________________③人体大约有2万5千亿个红细胞,2万5千亿=______________________④北京故宫博物馆占地面积约为72000=____________________
8、成立的条件是__________________
9、若,则k的值是__________________________
10、若,则x的值是________________________
11、若5x-3y-2=0,则_____________________
三、拓展探究:
1、计算,使结果只含有正整指数幂
① ②
2、若,试比较的大小。
