7.3.2 正弦型函数的性质和图像-【新教材】2020-2021学年人教B版(2019)高中数学必修第三册同步练习(word含答案)
文档属性
| 名称 | 7.3.2 正弦型函数的性质和图像-【新教材】2020-2021学年人教B版(2019)高中数学必修第三册同步练习(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 13:00:23 | ||
图片预览

文档简介
7.3.2正弦型函数的性质和图像
一、选择题:
1.函数的周期、振幅和初相分别是( )。
A. B. C. D.
2.已知函数,则下列命题正确的是( )。
A、f(x)是周期为1的奇函数; B、f(x)是周期为2的偶函数;
C、f(x)是周期为1的非奇非偶函数; D、f(x)是周期为2的非奇非偶函数。
3、函数的图象的一条对称轴是( )。
A、x= B、x= - C、x= D、x=-
4、函数的图象( )。
A、关于直线x=对称; B、关于y轴对称;
C、关于直线x= -对称; D、关于原点对称;
5、先将函数y=sin2X的图象向右平移个单位长度,再将所得图象作关于y轴的对称变换,则与最后所得图象对应的函数解析式是( )。
A、 B、
C、 D、y= sin(-2x-)
6.将函数的图象上所有的点向右平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,所得图象的函数解析式是( )。
A、 B、
C、 D、
7、已知函数,下面结论错误的是( )。
A、函数的最小正周期为 B、函数在区间上是增函数
C、函数的图象关于直线对称 D、函数是奇函数
8.已知函数的周期为π,则其单调递增区间为( )。
A. B.
C. D.
9.当用“五点法”作的图像时,应当描出的五个关键点的横坐标可以是( )。
A. B.
C. D.
10.已知和函数图像的两条相邻对称轴,则
的值为( )。
A.4 B.8 C. D.
二、填空题:
1.函数的最大值为5,则A= 。
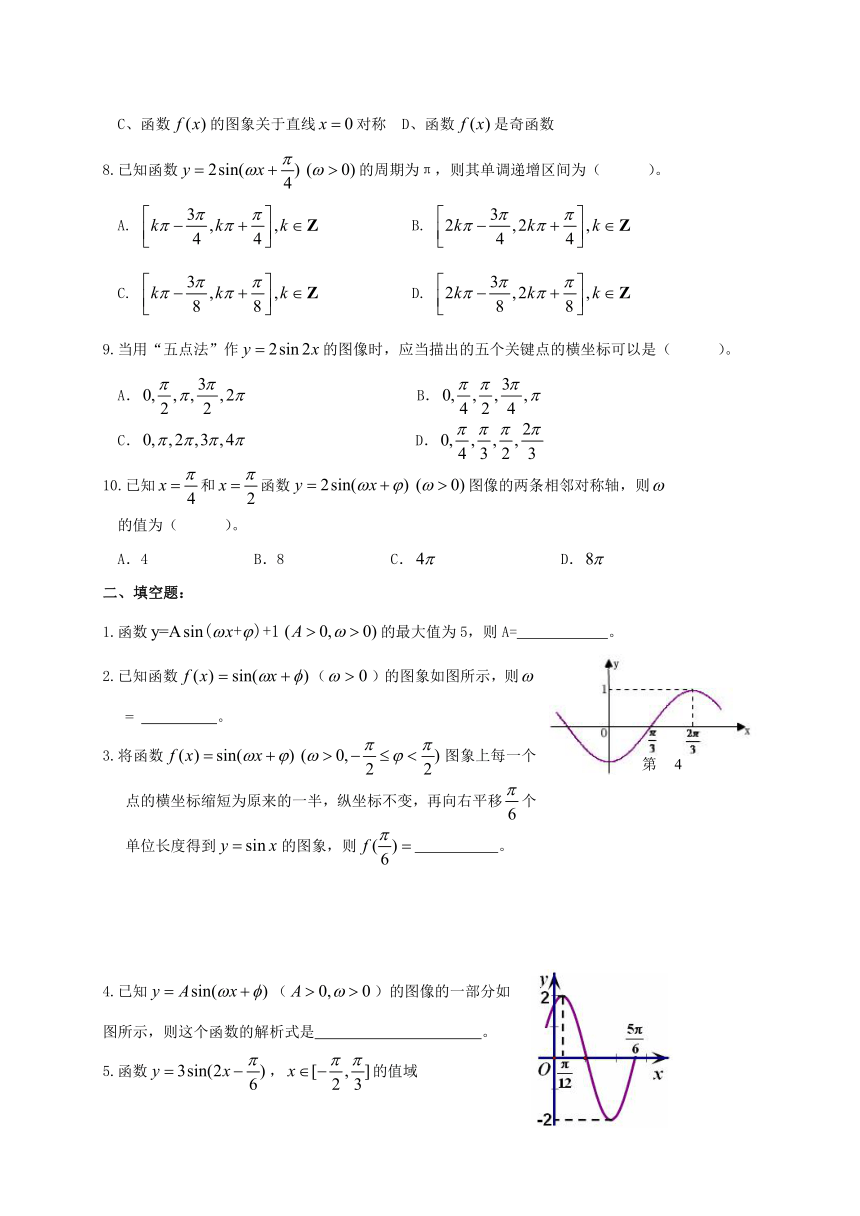
2.已知函数()的图象如图所示,则 = 。
3.将函数图象上每一个点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到的图象,则 。
4.已知()的图像的一部分如
图所示,则这个函数的解析式是 。
5.函数,的值域
为 。
6. 函数的对称轴方程为 ,对称中心
的坐标为为 。
三、解答题:
1、已知函数()在一个周期内的图象如图所示。求函数解析式。
2、函数()的部分图象如图所示,若,求函数解析式。
3、设函数,,且以为最小正周期。
(1)求;(2)求的解析式;(3)已知,求的值。
4.求函数的单调递增区间。
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C D C D C B A
二、填空题:
1.4 2.
3. 解:逆向推导:①的图象向左平移个单位长度:;
②图象上每一个点的横坐标伸长为原来2倍,纵坐
标不变:。
于是。。
4. 解:,,。A=2.
。取。所以函数的解析式为。
5.[-3,3]
6. 解:令,解得。
对称轴方程为:。令,解得。
所以对称中心坐标为:。
三、解答题:
1.解:A=2,,。
当x=0时,.所以可以取。
。
2. 解: A=,,,
。当时,.
所以。因为,所以取。函数的解析式为。
3.设函数,,且以为最小正周期。
(1)求;(2)求的解析式;(3)已知,求的值。
解:(1)因为,所以;
(2)因为,所以。的解析式为。
(3)。
因为,所以。
。
4.求函数的单调递增区间。
解:。
令,解得。
所以单调递减区间为。
令,解得。
所以单调递增减区间为。
一、选择题:
1.函数的周期、振幅和初相分别是( )。
A. B. C. D.
2.已知函数,则下列命题正确的是( )。
A、f(x)是周期为1的奇函数; B、f(x)是周期为2的偶函数;
C、f(x)是周期为1的非奇非偶函数; D、f(x)是周期为2的非奇非偶函数。
3、函数的图象的一条对称轴是( )。
A、x= B、x= - C、x= D、x=-
4、函数的图象( )。
A、关于直线x=对称; B、关于y轴对称;
C、关于直线x= -对称; D、关于原点对称;
5、先将函数y=sin2X的图象向右平移个单位长度,再将所得图象作关于y轴的对称变换,则与最后所得图象对应的函数解析式是( )。
A、 B、
C、 D、y= sin(-2x-)
6.将函数的图象上所有的点向右平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,所得图象的函数解析式是( )。
A、 B、
C、 D、
7、已知函数,下面结论错误的是( )。
A、函数的最小正周期为 B、函数在区间上是增函数
C、函数的图象关于直线对称 D、函数是奇函数
8.已知函数的周期为π,则其单调递增区间为( )。
A. B.
C. D.
9.当用“五点法”作的图像时,应当描出的五个关键点的横坐标可以是( )。
A. B.
C. D.
10.已知和函数图像的两条相邻对称轴,则
的值为( )。
A.4 B.8 C. D.
二、填空题:
1.函数的最大值为5,则A= 。
2.已知函数()的图象如图所示,则 = 。
3.将函数图象上每一个点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到的图象,则 。
4.已知()的图像的一部分如
图所示,则这个函数的解析式是 。
5.函数,的值域
为 。
6. 函数的对称轴方程为 ,对称中心
的坐标为为 。
三、解答题:
1、已知函数()在一个周期内的图象如图所示。求函数解析式。
2、函数()的部分图象如图所示,若,求函数解析式。
3、设函数,,且以为最小正周期。
(1)求;(2)求的解析式;(3)已知,求的值。
4.求函数的单调递增区间。
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C D C D C B A
二、填空题:
1.4 2.
3. 解:逆向推导:①的图象向左平移个单位长度:;
②图象上每一个点的横坐标伸长为原来2倍,纵坐
标不变:。
于是。。
4. 解:,,。A=2.
。取。所以函数的解析式为。
5.[-3,3]
6. 解:令,解得。
对称轴方程为:。令,解得。
所以对称中心坐标为:。
三、解答题:
1.解:A=2,,。
当x=0时,.所以可以取。
。
2. 解: A=,,,
。当时,.
所以。因为,所以取。函数的解析式为。
3.设函数,,且以为最小正周期。
(1)求;(2)求的解析式;(3)已知,求的值。
解:(1)因为,所以;
(2)因为,所以。的解析式为。
(3)。
因为,所以。
。
4.求函数的单调递增区间。
解:。
令,解得。
所以单调递减区间为。
令,解得。
所以单调递增减区间为。
