6.1分类加法计数原理与分步乘法计数原理-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修三练习(word含答案解析)
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修三练习(word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 199.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览




文档简介
分类加法计数原理与分步乘法计数原理练习
一、单选题
如图所示,从甲地到乙地有3条公路可走,从乙地到丙地有2条公路可走,从甲地不经过乙地到丙地有2条水路可走.则从甲地经过乙地到丙地和从甲地到丙地的走法种数分别为(????)
A. 6,8 B. 6,6 C. 5,7 D. 6,2
某班组织文艺晚会,准备从A,B等8个节目中选出4个节目演出,要求A,B两个节目至少有一个被选中,且A,B同时被选中时,它们的演出顺序不能相邻,那么不同的演出顺序种数为(? )
A. 1020 B. 1140 C. 1320 D. 1860
从标号分别为1、2、3、4的四个红球和标号分别为1、2、3的三个黑球及标号分别为1、2的两个白球中取出不同颜色的两个小球,不同的取法种数共有(????)
A. 24种 B. 9种 C. 10种 D. 26种
有不同的语文书9本,不同的数学书7本,不同的英语书5本,从中选出不属于同一学科的书2本,则不同的选法有(????)
A. 21种 B. 315种 C. 153种 D. 143种
某电视台在一档娱乐节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众的来信,甲信箱中有30封,乙信箱中有20封.现由主持人抽奖确定幸运观众,若先从这些信中确定一名幸运观众为“幸运之星”,再从两信箱中各确定一名幸运观众为“幸运伙伴”(“幸运之星”与“幸运伙伴”不能为同一人),不同的结果有(????).
A. 17400种 B. 11400种 C. 28800种 D. 29000种
如图,洛书(古称龟书),是阴阳五行术数之源.在古代传说中有神龟出于洛水,其甲壳上有此图像,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.若从四个阴数和五个阳数中随机选取3个数,则选取的3个数之和为奇数的方法数为
A. 30 B. 40 C. 44 D. 70
若用0,1,2,3,4,5这6个数字组成无重复数字且个位数字不是5的六位数,则这样的六位数共有(????)个
A. 470 B. 504 C. 540 D. 288
5个人排成一排,其中甲与乙不相邻,而丙与丁必须相邻,则不同的排法种数为(????)
A. 72 B. 48 C. 24 D. 60
如图所示的阴影部分由方格纸上3个小方格组成,我们称这样的图案为“L”形(每次旋转90?仍为“L”形的图案),那么在5×6的方格纸上可以画出不同位置的“L”形图案的个数是(????)
A. 36
B. 64
C. 80
D. 96
用5种不同颜色(可以只用其中部分颜色)给三棱锥P?ABC的各条棱染色,要求任意两条有公共端点的棱颜色不同,则不同的染色方法共有(????)
A. 180种
B. 432种
C. 540种
D. 780种
将甲、乙、丙、丁四位辅导老师分配到A、B、C、D四个班级,每个班级一位老师,且甲不能分配到A班,丁不能分配到B班,则共有分配方案的种数为(? )
A. 10 B. 12 C. 14 D. 24
满足a,b∈?1,0,1,2且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为(????)
A. 14 B. 13 C. 12 D. 10
二、单空题
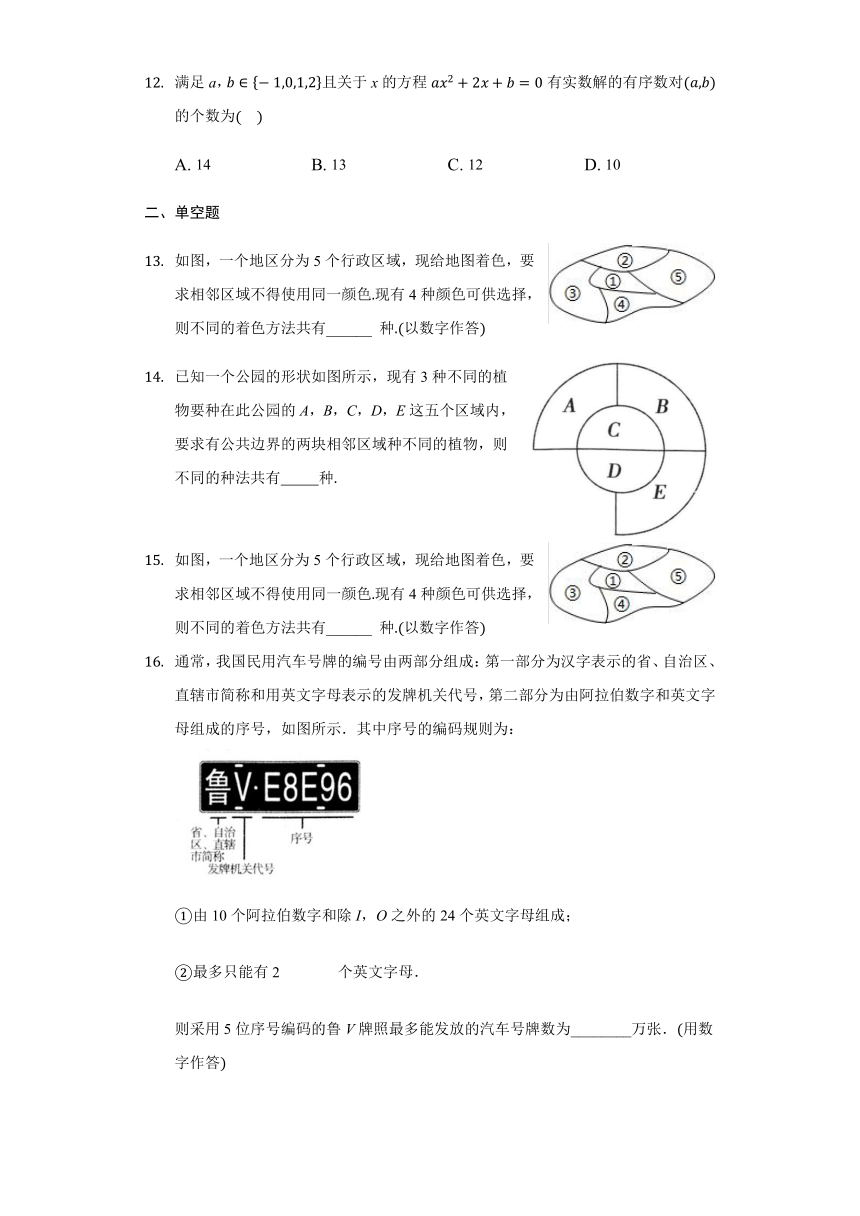
如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色.现有4种颜色可供选择,则不同的着色方法共有______ 种.(以数字作答)
已知一个公园的形状如图所示,现有3种不同的植物要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的两块相邻区域种不同的植物,则不同的种法共有??????????种.
如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色.现有4种颜色可供选择,则不同的着色方法共有______ 种.(以数字作答)
通常,我国民用汽车号牌的编号由两部分组成:第一部分为汉字表示的省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图所示.其中序号的编码规则为:
①由10个阿拉伯数字和除I,O之外的24个英文字母组成;
②最多只能有2个英文字母.
则采用5位序号编码的鲁V牌照最多能发放的汽车号牌数为________万张.(用数字作答)
如图所示为一电路图,从A到B不同的线路中可通电的共有________条.
三、解答题
用黄、蓝、白三种颜色粉刷6间办公室.
(1)若每间办公室刷什么颜色不要求,有多少种不同的粉刷方法?
(2)若一种颜色的粉刷3间,一种颜色的粉刷2间,一种颜色的粉刷1间,有多少种不同的粉刷方法?
(3)若每种颜色至少用一次,粉刷这6间办公室,有多少种不同的粉刷方法?
现有高一四个班的学生34人,其中一、二、三、四班分别有7人、8人、9人、10人,他们自愿组成数学课外小组.
(1)选其中一人为负责人,有多少种不同的选法?
(2)每班选一名组长,有多少种不同的选法?
(3)推选两人做中心发言,这两人需来自不同的班级,有多少种不同的选法?
有一项活动需在3名老师,6名男同学和8名女同学中选人参加,
(1)若只需一人参加,有多少种不同选法?
(2)若需一名老师,一名学生参加,有多少种不同选法?
(3)若需老师,男同学、女同学各一人参加,有多少种不同选法?
答案和解析
1.【答案】A
【解答】解:根据分步乘法计数原理,
可知从甲地经过乙地到丙地的走法种数为2×3=6;
又从甲地不经过乙地到丙地有2条水路可走,
由分类加法计数原理,可得从甲地到丙地的走法种数为6+2=8.
2.【答案】B
【解答】
解:分两类:第一类,A,B只有一个选中,则不同演出顺序有C21C63A44种;
第二类:A,B同时选中,则不同演出顺序有C62A22A32种,
共有:C21C63A44+C62A22A32=1140(种).
3.【答案】D
【解答】
解:红球和黑球中各取一个,共有4×3=12种,
红球和白球中各取一个,共有4×2=8种,
白球和黑球中各取一个,共有2×3=6种,
根据分类计数原理,共有12+8+6=26中,
4.【答案】D
【解答】
解:可分三类:第一类:语文、数学各1本,共有9×7=63种;
第二类:语文、英语各1本,共有9×5=45种;
第三类:数学、英语各1本,共有7×5=35种,
∴共有63+45+35=143种不同的选法.
5.【答案】C
【解答】
解:由题意知本题是一个分两类计数问题,
幸运之星在甲箱中抽,先定幸运之星,
再在两箱中各定一名幸运伙伴有30×29×20=17400种结果;
幸运之星在乙箱中抽,同理有20×19×30=11400(种)结果,
因此共有不同结果17400+11400=28800(种).
6.【答案】B
【解答】
解:从四个阴数2,4,6,8和五个阳数1,3,5,7,9中随机选取3个数,和为奇数,则分两种情况:1个阳数,2个阴数,或者3个阳数.
①1个阳数,2个阴数:C51C42=30种不同方法;
②3个阳数:C53=10种不同方法,
故共有30+10=40种方法.
7.【答案】B
【解答】
解:由分类加法计数原理,
当首位是5时:后五位共有A55=120个;
当首位不是5时:依次排首、末、中间四位共有C41C41A44=384个;
综上,共有120+384=504个六位数.
8.【答案】C
【解答】
解:首先丙丁采取捆绑法,看做一个人,且丙丁有顺序,排法有A44×A22=48种,
又因为有甲乙相邻的情况在里面,所以把甲乙也看成一个,这就剩三人排了共有6种排法,再考虑甲乙顺序、丙丁顺序则共有6×2×2=24种排法.
所以最后作差可得不同的排法种数为24种.
9.【答案】C
【解答】解:每一个“田”字里可以画出4个“L”形图案,如图.
因为5×6的方格纸内共有4×5=20个“田”字,所以可以画出20×4=80个“L”形图案.
10.【答案】D
【解答】
解:四面体的对棱可以涂同一种颜色,也可以涂不同的颜色,
①若所有相对的棱涂同一种颜色,则一共用了三种颜色,不同的涂色方案共有A53=60?种;
②若相对3对对棱中有2对对棱涂同色,则一共用了4种颜色,不同的涂色方案共有C32A54=360种;
③若相对3对对棱中有1对对棱涂同色,则一共用了5种颜色,不同的涂色方案共有C31A55=360种.
综上可得,总的涂法种数是60+360+360=780种,
11.【答案】C
【解答】
解:①甲到B班,则丁有3种选择,剩下两人自由分,有3×2=6种方法;
②甲没到B班,则甲有两种选择,再安排丁,有两种方法,剩余两人自由分,有2×2×2=8种方法,
根据分类加法计数原理,共有分配方案的种数为6+8=14种.
12.【答案】B
【解答】
解:当a=0时,易知满足题意的(a,b)有4个;
当a≠0时,需Δ=4?4ab≥0,即ab≤1,
当a=?1时,b的取值有4个,
当a=1时,b的取值有3个,
当a=2时,b的取值有2个,所以满足题意的(a,b)有9个.
综上,满足题意的有序数对(a,b)的个数为4+9=13,
13.【答案】72
【解答】
解:由题意,选用3种颜色时:则?②?④同色,?③?⑤同色,涂色方法:C43A33=24种,
4色全用时涂色方法:则?②?④或?③?⑤用一种颜色,涂色方法:C21A44=48种,
所以不同的着色方法共有24+48=72种.
故答案为72.
14.【答案】18
【解答】解:分两步进行:
?①对于A,B,C区域,三个区域两两相邻,种植的植物都不能相同,
将3种不同的植物全排列,安排在A,B,C区域,有A33=6种种法;
?②对于D,E区域,若C,E相同,D有2种种法,
若C,E不相同,D只有1种种法,故D,E区域不同的种法共有2+1=3(种).
由分步乘法计数原理可得所有种法的种数为6×3=18.
15.【答案】72
【解答】
解:由题意,选用3种颜色时:则?②?④同色,?③?⑤同色,涂色方法:C43A33=24种,
4色全用时涂色方法:则?②?④或?③?⑤用一种颜色,涂色方法:C21A44=48种,
所以不同的着色方法共有24+48=72种.
故答案为72.
16.【答案】706
【解答】
解:分三类讨论,
①有1位英文字母时,有C51×24×104=120(万),
②有2位英文字母时,有C52×24×24×103=576(万),
③全是数字时,105=10(万),
满足规则的编码共有120+576+10=706(万).
故答案为706.
17.【答案】8
【解答】
解:按上、中、下三条线路可分为三类:
从上线路中有3种;
中线路中有1种;
下线路中有2×2=4种,
根据分类计数原理,共有3+1+4=8(种).
故答案为8.
18.【答案】解:(1)根据题意,每间办公室刷什么颜色不要求,则每间办公室都有3种选择,即共有3×3×3×3×3×3=36=729种情况;
(2)根据题意,先将办公室分为3组,分别为3间、2间、1间,有C63C32C11种分法,
再将3组对应三种颜色,有A33种情况,
由分步计数原理可得,共有C63C32C11A33=360种粉刷方法;
(3)若每种颜色至少用一次,先将办公室分为3组,让每组用一种颜色,分析可得,有3间、2间、1间或2间、2间、2间或4间,1间、1间,
三种分组的方法:①若分为2间、2间、2间的情况,有C62C42C22A33种分法,将3组对应三种颜色,有A33种情况,则有C62C42C22A33A33=90种粉刷方法;
②若分为3间、2间、1间的情况,有C63C32C11种分法,将3组对应三种颜色,有A33种情况,则有C63C32C11A33=360种粉刷方法;
③若分为1间、1间、4间的情况,有C61C51C44A22种分法,将3组对应三种颜色,有A33种情况,则有C61C51C44A22A33=90种粉刷方法,
由分类计数原理,可得共有90+360+90=540种方法.
19.【答案】解:(1)根据题意,四个班共34人,
要求从34人中,选其中一人为负责人,
即有34种选法;
(2)根据题意,分析可得:从一班选一名组长,有7种情况,
从二班选一名组长,有8种情况,
从三班选一名组长,有9种情况,
从四班选一名组长,有10种情况,
所以每班选一名组长,不同的选法共有:7×8×9×10=5040(种).
(3)根据题意,分六种情况讨论,
①从一、二班学生中各选1人,有7×8种不同的选法;
②从一、三班学生中各选1人,有7×9种不同的选法,
③从一、四班学生中各选1人,有7×10种不同的选法;
④从二、三班学生中各选1人,有8×9种不同的选法;
⑤从二、四班学生中各选1人,有8×10种不同的选法;
⑥从三、四班学生中各选1人,有9×10种不同的选法,
所以不同的选法共有:7×8+7×9+7×10+8×9+8×10+9×10=431(种).
20.【答案】解:(1)只需一人参加,可按老师、男同学、女同学分三类各自有3、6、8种方法,由分类加法计数原理知,总方法数为3+6+8=17(种).
(2)分两步,先选教师共3种选法,再选学生共6+8=14种选法,由分步乘法计数原理知,总方法数为3×14=42(种).
(3)教师、男、女同学各一人可分三步,每步方法依次为3,6,8种.由分步乘法计数原理知方法数为3×6×8=144(种).
一、单选题
如图所示,从甲地到乙地有3条公路可走,从乙地到丙地有2条公路可走,从甲地不经过乙地到丙地有2条水路可走.则从甲地经过乙地到丙地和从甲地到丙地的走法种数分别为(????)
A. 6,8 B. 6,6 C. 5,7 D. 6,2
某班组织文艺晚会,准备从A,B等8个节目中选出4个节目演出,要求A,B两个节目至少有一个被选中,且A,B同时被选中时,它们的演出顺序不能相邻,那么不同的演出顺序种数为(? )
A. 1020 B. 1140 C. 1320 D. 1860
从标号分别为1、2、3、4的四个红球和标号分别为1、2、3的三个黑球及标号分别为1、2的两个白球中取出不同颜色的两个小球,不同的取法种数共有(????)
A. 24种 B. 9种 C. 10种 D. 26种
有不同的语文书9本,不同的数学书7本,不同的英语书5本,从中选出不属于同一学科的书2本,则不同的选法有(????)
A. 21种 B. 315种 C. 153种 D. 143种
某电视台在一档娱乐节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众的来信,甲信箱中有30封,乙信箱中有20封.现由主持人抽奖确定幸运观众,若先从这些信中确定一名幸运观众为“幸运之星”,再从两信箱中各确定一名幸运观众为“幸运伙伴”(“幸运之星”与“幸运伙伴”不能为同一人),不同的结果有(????).
A. 17400种 B. 11400种 C. 28800种 D. 29000种
如图,洛书(古称龟书),是阴阳五行术数之源.在古代传说中有神龟出于洛水,其甲壳上有此图像,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.若从四个阴数和五个阳数中随机选取3个数,则选取的3个数之和为奇数的方法数为
A. 30 B. 40 C. 44 D. 70
若用0,1,2,3,4,5这6个数字组成无重复数字且个位数字不是5的六位数,则这样的六位数共有(????)个
A. 470 B. 504 C. 540 D. 288
5个人排成一排,其中甲与乙不相邻,而丙与丁必须相邻,则不同的排法种数为(????)
A. 72 B. 48 C. 24 D. 60
如图所示的阴影部分由方格纸上3个小方格组成,我们称这样的图案为“L”形(每次旋转90?仍为“L”形的图案),那么在5×6的方格纸上可以画出不同位置的“L”形图案的个数是(????)
A. 36
B. 64
C. 80
D. 96
用5种不同颜色(可以只用其中部分颜色)给三棱锥P?ABC的各条棱染色,要求任意两条有公共端点的棱颜色不同,则不同的染色方法共有(????)
A. 180种
B. 432种
C. 540种
D. 780种
将甲、乙、丙、丁四位辅导老师分配到A、B、C、D四个班级,每个班级一位老师,且甲不能分配到A班,丁不能分配到B班,则共有分配方案的种数为(? )
A. 10 B. 12 C. 14 D. 24
满足a,b∈?1,0,1,2且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为(????)
A. 14 B. 13 C. 12 D. 10
二、单空题
如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色.现有4种颜色可供选择,则不同的着色方法共有______ 种.(以数字作答)
已知一个公园的形状如图所示,现有3种不同的植物要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的两块相邻区域种不同的植物,则不同的种法共有??????????种.
如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色.现有4种颜色可供选择,则不同的着色方法共有______ 种.(以数字作答)
通常,我国民用汽车号牌的编号由两部分组成:第一部分为汉字表示的省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图所示.其中序号的编码规则为:
①由10个阿拉伯数字和除I,O之外的24个英文字母组成;
②最多只能有2个英文字母.
则采用5位序号编码的鲁V牌照最多能发放的汽车号牌数为________万张.(用数字作答)
如图所示为一电路图,从A到B不同的线路中可通电的共有________条.
三、解答题
用黄、蓝、白三种颜色粉刷6间办公室.
(1)若每间办公室刷什么颜色不要求,有多少种不同的粉刷方法?
(2)若一种颜色的粉刷3间,一种颜色的粉刷2间,一种颜色的粉刷1间,有多少种不同的粉刷方法?
(3)若每种颜色至少用一次,粉刷这6间办公室,有多少种不同的粉刷方法?
现有高一四个班的学生34人,其中一、二、三、四班分别有7人、8人、9人、10人,他们自愿组成数学课外小组.
(1)选其中一人为负责人,有多少种不同的选法?
(2)每班选一名组长,有多少种不同的选法?
(3)推选两人做中心发言,这两人需来自不同的班级,有多少种不同的选法?
有一项活动需在3名老师,6名男同学和8名女同学中选人参加,
(1)若只需一人参加,有多少种不同选法?
(2)若需一名老师,一名学生参加,有多少种不同选法?
(3)若需老师,男同学、女同学各一人参加,有多少种不同选法?
答案和解析
1.【答案】A
【解答】解:根据分步乘法计数原理,
可知从甲地经过乙地到丙地的走法种数为2×3=6;
又从甲地不经过乙地到丙地有2条水路可走,
由分类加法计数原理,可得从甲地到丙地的走法种数为6+2=8.
2.【答案】B
【解答】
解:分两类:第一类,A,B只有一个选中,则不同演出顺序有C21C63A44种;
第二类:A,B同时选中,则不同演出顺序有C62A22A32种,
共有:C21C63A44+C62A22A32=1140(种).
3.【答案】D
【解答】
解:红球和黑球中各取一个,共有4×3=12种,
红球和白球中各取一个,共有4×2=8种,
白球和黑球中各取一个,共有2×3=6种,
根据分类计数原理,共有12+8+6=26中,
4.【答案】D
【解答】
解:可分三类:第一类:语文、数学各1本,共有9×7=63种;
第二类:语文、英语各1本,共有9×5=45种;
第三类:数学、英语各1本,共有7×5=35种,
∴共有63+45+35=143种不同的选法.
5.【答案】C
【解答】
解:由题意知本题是一个分两类计数问题,
幸运之星在甲箱中抽,先定幸运之星,
再在两箱中各定一名幸运伙伴有30×29×20=17400种结果;
幸运之星在乙箱中抽,同理有20×19×30=11400(种)结果,
因此共有不同结果17400+11400=28800(种).
6.【答案】B
【解答】
解:从四个阴数2,4,6,8和五个阳数1,3,5,7,9中随机选取3个数,和为奇数,则分两种情况:1个阳数,2个阴数,或者3个阳数.
①1个阳数,2个阴数:C51C42=30种不同方法;
②3个阳数:C53=10种不同方法,
故共有30+10=40种方法.
7.【答案】B
【解答】
解:由分类加法计数原理,
当首位是5时:后五位共有A55=120个;
当首位不是5时:依次排首、末、中间四位共有C41C41A44=384个;
综上,共有120+384=504个六位数.
8.【答案】C
【解答】
解:首先丙丁采取捆绑法,看做一个人,且丙丁有顺序,排法有A44×A22=48种,
又因为有甲乙相邻的情况在里面,所以把甲乙也看成一个,这就剩三人排了共有6种排法,再考虑甲乙顺序、丙丁顺序则共有6×2×2=24种排法.
所以最后作差可得不同的排法种数为24种.
9.【答案】C
【解答】解:每一个“田”字里可以画出4个“L”形图案,如图.
因为5×6的方格纸内共有4×5=20个“田”字,所以可以画出20×4=80个“L”形图案.
10.【答案】D
【解答】
解:四面体的对棱可以涂同一种颜色,也可以涂不同的颜色,
①若所有相对的棱涂同一种颜色,则一共用了三种颜色,不同的涂色方案共有A53=60?种;
②若相对3对对棱中有2对对棱涂同色,则一共用了4种颜色,不同的涂色方案共有C32A54=360种;
③若相对3对对棱中有1对对棱涂同色,则一共用了5种颜色,不同的涂色方案共有C31A55=360种.
综上可得,总的涂法种数是60+360+360=780种,
11.【答案】C
【解答】
解:①甲到B班,则丁有3种选择,剩下两人自由分,有3×2=6种方法;
②甲没到B班,则甲有两种选择,再安排丁,有两种方法,剩余两人自由分,有2×2×2=8种方法,
根据分类加法计数原理,共有分配方案的种数为6+8=14种.
12.【答案】B
【解答】
解:当a=0时,易知满足题意的(a,b)有4个;
当a≠0时,需Δ=4?4ab≥0,即ab≤1,
当a=?1时,b的取值有4个,
当a=1时,b的取值有3个,
当a=2时,b的取值有2个,所以满足题意的(a,b)有9个.
综上,满足题意的有序数对(a,b)的个数为4+9=13,
13.【答案】72
【解答】
解:由题意,选用3种颜色时:则?②?④同色,?③?⑤同色,涂色方法:C43A33=24种,
4色全用时涂色方法:则?②?④或?③?⑤用一种颜色,涂色方法:C21A44=48种,
所以不同的着色方法共有24+48=72种.
故答案为72.
14.【答案】18
【解答】解:分两步进行:
?①对于A,B,C区域,三个区域两两相邻,种植的植物都不能相同,
将3种不同的植物全排列,安排在A,B,C区域,有A33=6种种法;
?②对于D,E区域,若C,E相同,D有2种种法,
若C,E不相同,D只有1种种法,故D,E区域不同的种法共有2+1=3(种).
由分步乘法计数原理可得所有种法的种数为6×3=18.
15.【答案】72
【解答】
解:由题意,选用3种颜色时:则?②?④同色,?③?⑤同色,涂色方法:C43A33=24种,
4色全用时涂色方法:则?②?④或?③?⑤用一种颜色,涂色方法:C21A44=48种,
所以不同的着色方法共有24+48=72种.
故答案为72.
16.【答案】706
【解答】
解:分三类讨论,
①有1位英文字母时,有C51×24×104=120(万),
②有2位英文字母时,有C52×24×24×103=576(万),
③全是数字时,105=10(万),
满足规则的编码共有120+576+10=706(万).
故答案为706.
17.【答案】8
【解答】
解:按上、中、下三条线路可分为三类:
从上线路中有3种;
中线路中有1种;
下线路中有2×2=4种,
根据分类计数原理,共有3+1+4=8(种).
故答案为8.
18.【答案】解:(1)根据题意,每间办公室刷什么颜色不要求,则每间办公室都有3种选择,即共有3×3×3×3×3×3=36=729种情况;
(2)根据题意,先将办公室分为3组,分别为3间、2间、1间,有C63C32C11种分法,
再将3组对应三种颜色,有A33种情况,
由分步计数原理可得,共有C63C32C11A33=360种粉刷方法;
(3)若每种颜色至少用一次,先将办公室分为3组,让每组用一种颜色,分析可得,有3间、2间、1间或2间、2间、2间或4间,1间、1间,
三种分组的方法:①若分为2间、2间、2间的情况,有C62C42C22A33种分法,将3组对应三种颜色,有A33种情况,则有C62C42C22A33A33=90种粉刷方法;
②若分为3间、2间、1间的情况,有C63C32C11种分法,将3组对应三种颜色,有A33种情况,则有C63C32C11A33=360种粉刷方法;
③若分为1间、1间、4间的情况,有C61C51C44A22种分法,将3组对应三种颜色,有A33种情况,则有C61C51C44A22A33=90种粉刷方法,
由分类计数原理,可得共有90+360+90=540种方法.
19.【答案】解:(1)根据题意,四个班共34人,
要求从34人中,选其中一人为负责人,
即有34种选法;
(2)根据题意,分析可得:从一班选一名组长,有7种情况,
从二班选一名组长,有8种情况,
从三班选一名组长,有9种情况,
从四班选一名组长,有10种情况,
所以每班选一名组长,不同的选法共有:7×8×9×10=5040(种).
(3)根据题意,分六种情况讨论,
①从一、二班学生中各选1人,有7×8种不同的选法;
②从一、三班学生中各选1人,有7×9种不同的选法,
③从一、四班学生中各选1人,有7×10种不同的选法;
④从二、三班学生中各选1人,有8×9种不同的选法;
⑤从二、四班学生中各选1人,有8×10种不同的选法;
⑥从三、四班学生中各选1人,有9×10种不同的选法,
所以不同的选法共有:7×8+7×9+7×10+8×9+8×10+9×10=431(种).
20.【答案】解:(1)只需一人参加,可按老师、男同学、女同学分三类各自有3、6、8种方法,由分类加法计数原理知,总方法数为3+6+8=17(种).
(2)分两步,先选教师共3种选法,再选学生共6+8=14种选法,由分步乘法计数原理知,总方法数为3×14=42(种).
(3)教师、男、女同学各一人可分三步,每步方法依次为3,6,8种.由分步乘法计数原理知方法数为3×6×8=144(种).
