2020-2021学年 人教版八年级数学下册 20.1.1.2 用样本平均数估计总体平均数 同步练习题 (word版含答案)
文档属性
| 名称 | 2020-2021学年 人教版八年级数学下册 20.1.1.2 用样本平均数估计总体平均数 同步练习题 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 154.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览



文档简介
第二十章 数据的分析
20.1 数据的集中趋势
20.1.1.2
用样本平均数估计总体平均数
1.对一组数据进行了整理,结果如下表:
分组
0≤x<10
10≤x<20
频数
8
12
则这组数据的平均数约是(
)
A.10 B.11 C.12 D.16
2.
某学校绿化小组22人参加一次植树活动,其中4人每人种6棵,8人每人种3棵,10人每人种4棵,那么这个小组平均每人种树的棵数为(
)
A.6
B.5
C.4
D.3
3.某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量.数据如下
(单位:只):7,5,7,8,7,5,8,9,5,9.利用上述数据估计该小区2000户家庭一周内需要环保方便袋约(
)
A.2000只
B.14000只
C.21000只
D.98000只
4.如图所示是小芹6月1日~7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是(
)
A.1小时
B.1.5小时
C.2小时
D.3小时
6.下列各组数据中,组中值不是10的是(
)
A.0≤x<20
B.8≤x<12
C.7≤x<13
D.3≤x<7
7.为了调查某一路口某一时段的汽车流量,记录了一个月中每天该时段通过该路口的汽车数量,其中有4天每天是284辆,4天每天是290辆人,12天每天是312辆,10天每天是314辆人,于是可以估计这一路口该时段每天通过汽车的平均数约为(
)
A.305辆
B.306辆
C.307辆
D.308辆
7.已知一组数据在10≤x<20的范围内出现了7次,则组中值是
,权是
.
8.
某市号召居民节约用水,为了解某小区居民的用水情况,随机抽查了20户家庭某月的用水量,结果如表,则该小区500户家庭这个月的用水总量是
吨.
用水量(吨)
4
5
6
8
户数(户)
3
8
4
5
9.
某校组织学生参加植树活动,活动结束后,统计了八年级甲班50名学生每人植树的情况,绘制了如下的统计表:
植树棵数
3
4
5
6
人数
20
15
10
5
那么这50名学生平均每人植树
棵.
10.某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(分数为整数,满分为100分):
分数段(分)
61~70
71~80
81~90
91~100
人 数
2
8
6
4
则参加这次演讲比赛的同学的平均分为
.
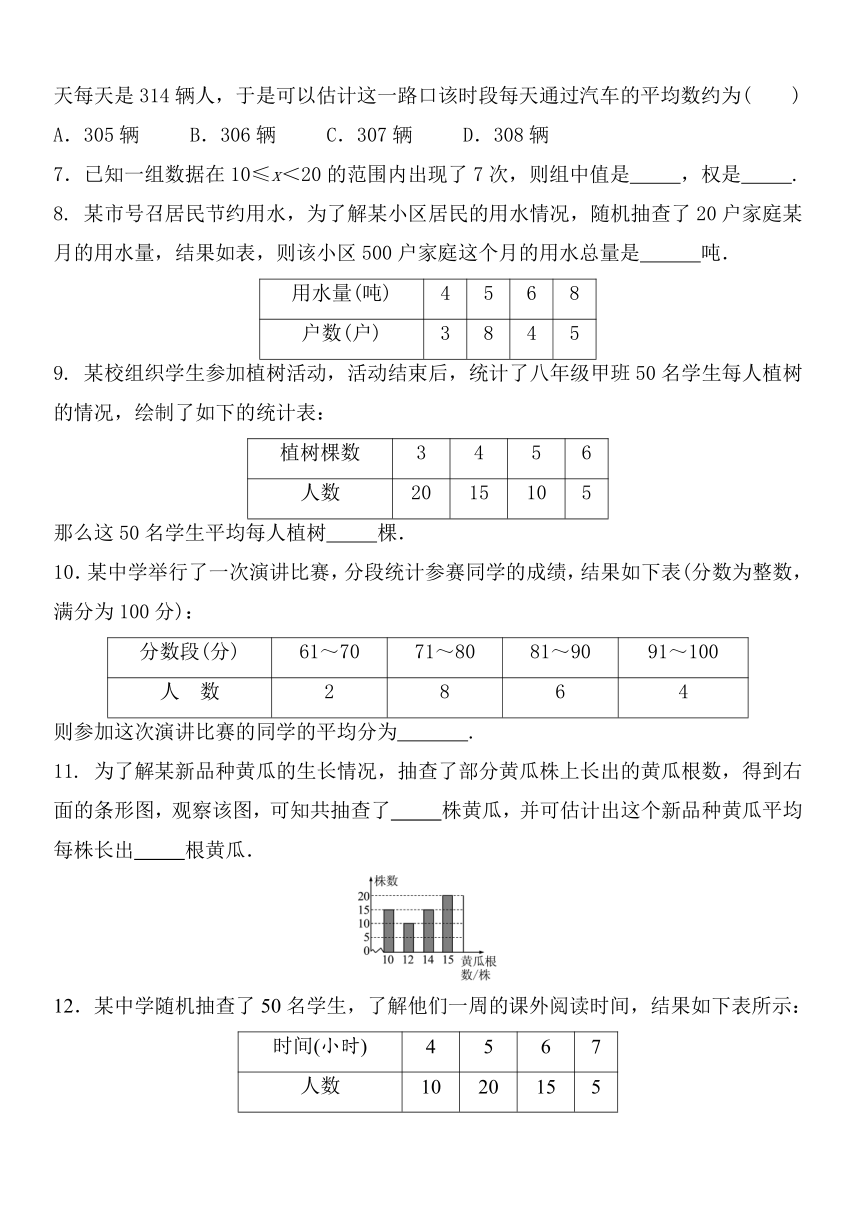
11.
为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,观察该图,可知共抽查了
株黄瓜,并可估计出这个新品种黄瓜平均每株长出
根黄瓜.
12.某中学随机抽查了50名学生,了解他们一周的课外阅读时间,结果如下表所示:
时间(小时)
4
5
6
7
人数
10
20
15
5
则这50名学生一周的平均课外阅读时间是
小时.
13.
若35≤x<47,则组中值为
.
14.
某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量
(单位:棵)
4
5
6
8
10
人数
30
22
25
15
8
则这100名学生平均每人植树
棵;若该校共有1000名学生,估计该校学生的植树总数是
棵.
15.
某中学为了了解本校学生的身体发育情况,抽测了同年龄的40名女学生的身高情况,统计人员将数据整理后,列出了频数分布表如下:
身高(cm)
频数
144.5≤x<149.5
2
149.5≤x<154.5
A
154.5≤x<159.5
14
159.5≤x<164.5
12
164.5≤x<169.5
6
合计
40
根据以上信息回答下列问题:
(1)频数分布表中的A=
;
(2)这40名女学生的平均身高大约是
cm
(精确到0.1cm).
16.
为了了解中学生的身体发育情况,对某中学同龄的60名女学生的身高进行了测量,并将结果列成了如下的频数分布表:
17.某市电信局对计算机拨号上网用户提供三种付费方式供用户选择(每个用户只能选择一种付费方式):甲种方式是按实际用时付费,每小时付信息费4元,另加付电话费每小时1元2角;乙种方式是包月制,每月付信息费100元,同时加付电话费每小时1元2角;丙种方式也是包月制,每月付信息费150元,但不必再另付电话费.某用户为选择合适的付费方式,连续记录了7天中每天上网所花的时间(单位:分):
第一天
第二天
第三天
第四天
第五天
第六天
第七天
上网时间(分)
62
40
35
74
27
60
80
根据上述情况,该用户选择哪种付费方式比较合适?请你帮助选择,并说明理由(每月以30天计算).
18.某地区在一次八年级数学检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a=
,b=
,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的八年级学生来说属于哪一类?
19.
统计2019年某博览会前20天日参观人数,得到如下频数分布表和如图所示的频数分布直方图(部分未完成):
2019年某博览会前20天日参观人数的频数分布表
组别(万人)
组中值(万人)
频数
7.5~14.5
11
5
14.5~21.5
6
21.5~28.5
25
28.5~35.5
32
3
2019年某博览会前20天日参观人数的频数分布直方图
(1)请补全频数分布表和频数分布直方图;
(2)求出日参观人数不低于22万人的天数和所占的百分比;
(3)利用以上信息,试估计该博览会(会期184天)的参观总人数.
20.
某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变,有关数据如下表所示:
景点
A
B
C
D
E
原价(元)
10
10
15
20
25
现价(元)
5
5
15
25
30
平均日人数(千人)
1
1
2
3
2
(1)该风景区称调整前后这5个景点门票的平均收费不变,平均日总收入持平.问风景区是怎样计算的?
(2)另一方面,游客认为调整收费后风景区的平均日总收入相对于调价前,实际上增加了约9.4%.问游客是怎样计算的?
(3)你认为风景区和游客哪一个的说法较能反映整体实际?
答案:
1-6
BCBBD
B
7.
15
7
8.
2900
9.
4
10.
8105
11.
60
13
12.
5.3
13.
41
14.
5.8
5800
15.
(1)
6
(2)
158.8
16.
解:
∵各组组中值分别为147,150,153,156,159,162,165,168,所以这60名女生的平均身高约为(147×1+150×3+153×6+156×8+159×18+162×11+165×10+168×3)÷60≈159.4(cm).
答:这60名女生的平均身高约为159.4cm.
17.
解:该用户一个月总上网时间约为×30÷60=27(时),选择甲种付费方式每月应付费5.2×27=140.4(元);选择乙种付费方式每月应付费100+1.2×27=132.4(元);选择丙种付费方式每月应付费150元.所以该用户选择乙种付费方式比较合适.
18.
解:(1)25 20 补全条形统计图略;
(2)由(1)可知,得满分的占20%,∴该地区此题得满分(即8分)的学生人数是4500×20%=900(人);
(3)由题意可得L===0.575.∵0.575处于0.4与0.7之间,∴此题对于该地区的八年级学生来说属于中等难度试题.
19.
解:(1)组中值为18,频数为6;
(2)日参观人数不低于22万人的有9天,所占百分比为45%;
(3)该博览会前20天的平均每天参观人数约为(11×5+18×6+25×6+32×3)÷20=20.45(万人),20.45×184=3762.8(万人).
20.
解:(1)风景区的算法是:调整前的平均价格为:×(10+10+15+20+25)=16(元);调整后的平均价格为:×(5+5+15+25+30)=16(元),而日平均人数没有变化,因此风景区的总收入没有变化;
(2)游客的计算方法:调整前风景区日平均收入为:10×1+10×1+15×2+20×3+25×2=160(千元);调整后风景区日平均收入为:5×1+5×1+15×2+25×3+30×2=175(千元),所以风景区的日平均收入增加了×100%≈9.4%;
(3)游客的说法较能反映整体实际.
20.1 数据的集中趋势
20.1.1.2
用样本平均数估计总体平均数
1.对一组数据进行了整理,结果如下表:
分组
0≤x<10
10≤x<20
频数
8
12
则这组数据的平均数约是(
)
A.10 B.11 C.12 D.16
2.
某学校绿化小组22人参加一次植树活动,其中4人每人种6棵,8人每人种3棵,10人每人种4棵,那么这个小组平均每人种树的棵数为(
)
A.6
B.5
C.4
D.3
3.某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量.数据如下
(单位:只):7,5,7,8,7,5,8,9,5,9.利用上述数据估计该小区2000户家庭一周内需要环保方便袋约(
)
A.2000只
B.14000只
C.21000只
D.98000只
4.如图所示是小芹6月1日~7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是(
)
A.1小时
B.1.5小时
C.2小时
D.3小时
6.下列各组数据中,组中值不是10的是(
)
A.0≤x<20
B.8≤x<12
C.7≤x<13
D.3≤x<7
7.为了调查某一路口某一时段的汽车流量,记录了一个月中每天该时段通过该路口的汽车数量,其中有4天每天是284辆,4天每天是290辆人,12天每天是312辆,10天每天是314辆人,于是可以估计这一路口该时段每天通过汽车的平均数约为(
)
A.305辆
B.306辆
C.307辆
D.308辆
7.已知一组数据在10≤x<20的范围内出现了7次,则组中值是
,权是
.
8.
某市号召居民节约用水,为了解某小区居民的用水情况,随机抽查了20户家庭某月的用水量,结果如表,则该小区500户家庭这个月的用水总量是
吨.
用水量(吨)
4
5
6
8
户数(户)
3
8
4
5
9.
某校组织学生参加植树活动,活动结束后,统计了八年级甲班50名学生每人植树的情况,绘制了如下的统计表:
植树棵数
3
4
5
6
人数
20
15
10
5
那么这50名学生平均每人植树
棵.
10.某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(分数为整数,满分为100分):
分数段(分)
61~70
71~80
81~90
91~100
人 数
2
8
6
4
则参加这次演讲比赛的同学的平均分为
.
11.
为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,观察该图,可知共抽查了
株黄瓜,并可估计出这个新品种黄瓜平均每株长出
根黄瓜.
12.某中学随机抽查了50名学生,了解他们一周的课外阅读时间,结果如下表所示:
时间(小时)
4
5
6
7
人数
10
20
15
5
则这50名学生一周的平均课外阅读时间是
小时.
13.
若35≤x<47,则组中值为
.
14.
某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量
(单位:棵)
4
5
6
8
10
人数
30
22
25
15
8
则这100名学生平均每人植树
棵;若该校共有1000名学生,估计该校学生的植树总数是
棵.
15.
某中学为了了解本校学生的身体发育情况,抽测了同年龄的40名女学生的身高情况,统计人员将数据整理后,列出了频数分布表如下:
身高(cm)
频数
144.5≤x<149.5
2
149.5≤x<154.5
A
154.5≤x<159.5
14
159.5≤x<164.5
12
164.5≤x<169.5
6
合计
40
根据以上信息回答下列问题:
(1)频数分布表中的A=
;
(2)这40名女学生的平均身高大约是
cm
(精确到0.1cm).
16.
为了了解中学生的身体发育情况,对某中学同龄的60名女学生的身高进行了测量,并将结果列成了如下的频数分布表:
17.某市电信局对计算机拨号上网用户提供三种付费方式供用户选择(每个用户只能选择一种付费方式):甲种方式是按实际用时付费,每小时付信息费4元,另加付电话费每小时1元2角;乙种方式是包月制,每月付信息费100元,同时加付电话费每小时1元2角;丙种方式也是包月制,每月付信息费150元,但不必再另付电话费.某用户为选择合适的付费方式,连续记录了7天中每天上网所花的时间(单位:分):
第一天
第二天
第三天
第四天
第五天
第六天
第七天
上网时间(分)
62
40
35
74
27
60
80
根据上述情况,该用户选择哪种付费方式比较合适?请你帮助选择,并说明理由(每月以30天计算).
18.某地区在一次八年级数学检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a=
,b=
,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的八年级学生来说属于哪一类?
19.
统计2019年某博览会前20天日参观人数,得到如下频数分布表和如图所示的频数分布直方图(部分未完成):
2019年某博览会前20天日参观人数的频数分布表
组别(万人)
组中值(万人)
频数
7.5~14.5
11
5
14.5~21.5
6
21.5~28.5
25
28.5~35.5
32
3
2019年某博览会前20天日参观人数的频数分布直方图
(1)请补全频数分布表和频数分布直方图;
(2)求出日参观人数不低于22万人的天数和所占的百分比;
(3)利用以上信息,试估计该博览会(会期184天)的参观总人数.
20.
某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变,有关数据如下表所示:
景点
A
B
C
D
E
原价(元)
10
10
15
20
25
现价(元)
5
5
15
25
30
平均日人数(千人)
1
1
2
3
2
(1)该风景区称调整前后这5个景点门票的平均收费不变,平均日总收入持平.问风景区是怎样计算的?
(2)另一方面,游客认为调整收费后风景区的平均日总收入相对于调价前,实际上增加了约9.4%.问游客是怎样计算的?
(3)你认为风景区和游客哪一个的说法较能反映整体实际?
答案:
1-6
BCBBD
B
7.
15
7
8.
2900
9.
4
10.
8105
11.
60
13
12.
5.3
13.
41
14.
5.8
5800
15.
(1)
6
(2)
158.8
16.
解:
∵各组组中值分别为147,150,153,156,159,162,165,168,所以这60名女生的平均身高约为(147×1+150×3+153×6+156×8+159×18+162×11+165×10+168×3)÷60≈159.4(cm).
答:这60名女生的平均身高约为159.4cm.
17.
解:该用户一个月总上网时间约为×30÷60=27(时),选择甲种付费方式每月应付费5.2×27=140.4(元);选择乙种付费方式每月应付费100+1.2×27=132.4(元);选择丙种付费方式每月应付费150元.所以该用户选择乙种付费方式比较合适.
18.
解:(1)25 20 补全条形统计图略;
(2)由(1)可知,得满分的占20%,∴该地区此题得满分(即8分)的学生人数是4500×20%=900(人);
(3)由题意可得L===0.575.∵0.575处于0.4与0.7之间,∴此题对于该地区的八年级学生来说属于中等难度试题.
19.
解:(1)组中值为18,频数为6;
(2)日参观人数不低于22万人的有9天,所占百分比为45%;
(3)该博览会前20天的平均每天参观人数约为(11×5+18×6+25×6+32×3)÷20=20.45(万人),20.45×184=3762.8(万人).
20.
解:(1)风景区的算法是:调整前的平均价格为:×(10+10+15+20+25)=16(元);调整后的平均价格为:×(5+5+15+25+30)=16(元),而日平均人数没有变化,因此风景区的总收入没有变化;
(2)游客的计算方法:调整前风景区日平均收入为:10×1+10×1+15×2+20×3+25×2=160(千元);调整后风景区日平均收入为:5×1+5×1+15×2+25×3+30×2=175(千元),所以风景区的日平均收入增加了×100%≈9.4%;
(3)游客的说法较能反映整体实际.
