23章一元二次方程复习课件
图片预览






文档简介
(共20张PPT)
一、问题
某校团委准备举办学生绘画展览,为了美化画面,在长为30cm、宽为20cm的矩形画面四周镶上宽度相等彩纸,并使彩纸的面积恰好与原画面面积相等(如图)。求彩纸的宽度。
解:设彩纸的宽度为 cm. 依题意得
整理得
20cm
30cm
这是一个什么方程
一元二次方程
(1)定义:只含有_____个未知数,且未知数的最高次数是____的整式方程,叫做一元二次方程。
(2)一元二次方程的一般形式是____________。其中____叫二次项,_____是二次项系数;_____叫一次项,______是一次项系数;______叫常数项。
1
2
回顾
(3)将方程 化为一元二次方程的一般形式是:_____________,它的二次项系数是____,一次项系数是___,常数项是___.
(4)在下列方程 中,是一元二次方程的有:_________________________.
5
-6
8
(1)
(2)
(3)
(4)
选择适当的方法求解下列方程
-----直接开平方法
-----配方法
-------公式法
----------因式分解法
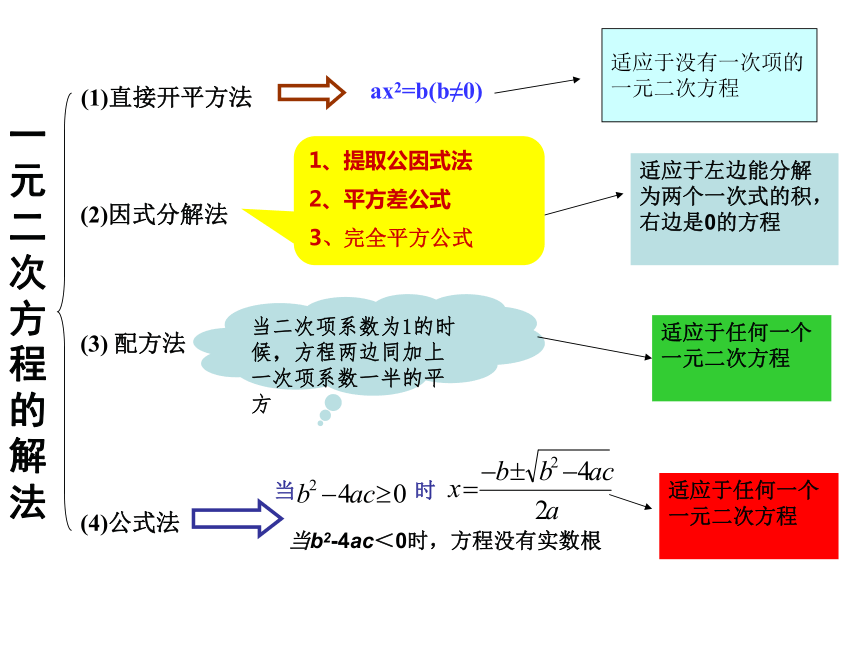
(1)直接开平方法
ax2=b(b≠0)
(2)因式分解法
1、提取公因式法
2、平方差公式
3、完全平方公式
(3) 配方法
(4)公式法
当二次项系数为1的时候,方程两边同加上一次项系数一半的平方
当b2-4ac<0时,方程没有实数根
一元二次方程的解法
适应于任何一个一元二次方程
适应于任何一个一元二次方程
适应于左边能分解为两个一次式的积,右边是0的方程
当 时
适应于没有一次项的
一元二次方程
(1) ---直接开平方法
解:
两边开平方
或
(2) -----配方法
解:
(3) -------公式法
解:
(4) -------因式分解法
解:
或
利用根与系数的关系,填写下表:
一元二次方程
若方程 有两个根 那么这两个根与方程的系数有什么关系
根与系数的关系
2
1
3
2
(2)若 是方程 的解,则 _____
(3)已知 是一元二次方程 的一个根,则方程的另一个根是_________.
(1)已知一元二次方程 的两个根为 . 则
试一试
效果检测
1、方程 的解是( )。
(A) (B) (C) ( D)
2、 是一元二次方程的条件是( )。
(A) (B) (C) (D)
3、解方程 ,配方得( )
(A) (B)
(C) (D)
c
D
c
4、为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600万元。则这两年投入教育经费的年平均增长率为多少?
解:
设这两年投入教育经费的年平均增长率为 ,依题意得
答:这两年投入教育经费的年平均增长率为20%。
即
(舍去)
小结:
2、通过本节课的学习大家有什么新的感受?
1、这节课我们复习了什么?
作业:用适当方法解下列方程
(5)
(1)
(2)
(4)
(3)
一、问题
某校团委准备举办学生绘画展览,为了美化画面,在长为30cm、宽为20cm的矩形画面四周镶上宽度相等彩纸,并使彩纸的面积恰好与原画面面积相等(如图)。求彩纸的宽度。
解:设彩纸的宽度为 cm. 依题意得
整理得
20cm
30cm
这是一个什么方程
一元二次方程
(1)定义:只含有_____个未知数,且未知数的最高次数是____的整式方程,叫做一元二次方程。
(2)一元二次方程的一般形式是____________。其中____叫二次项,_____是二次项系数;_____叫一次项,______是一次项系数;______叫常数项。
1
2
回顾
(3)将方程 化为一元二次方程的一般形式是:_____________,它的二次项系数是____,一次项系数是___,常数项是___.
(4)在下列方程 中,是一元二次方程的有:_________________________.
5
-6
8
(1)
(2)
(3)
(4)
选择适当的方法求解下列方程
-----直接开平方法
-----配方法
-------公式法
----------因式分解法
(1)直接开平方法
ax2=b(b≠0)
(2)因式分解法
1、提取公因式法
2、平方差公式
3、完全平方公式
(3) 配方法
(4)公式法
当二次项系数为1的时候,方程两边同加上一次项系数一半的平方
当b2-4ac<0时,方程没有实数根
一元二次方程的解法
适应于任何一个一元二次方程
适应于任何一个一元二次方程
适应于左边能分解为两个一次式的积,右边是0的方程
当 时
适应于没有一次项的
一元二次方程
(1) ---直接开平方法
解:
两边开平方
或
(2) -----配方法
解:
(3) -------公式法
解:
(4) -------因式分解法
解:
或
利用根与系数的关系,填写下表:
一元二次方程
若方程 有两个根 那么这两个根与方程的系数有什么关系
根与系数的关系
2
1
3
2
(2)若 是方程 的解,则 _____
(3)已知 是一元二次方程 的一个根,则方程的另一个根是_________.
(1)已知一元二次方程 的两个根为 . 则
试一试
效果检测
1、方程 的解是( )。
(A) (B) (C) ( D)
2、 是一元二次方程的条件是( )。
(A) (B) (C) (D)
3、解方程 ,配方得( )
(A) (B)
(C) (D)
c
D
c
4、为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600万元。则这两年投入教育经费的年平均增长率为多少?
解:
设这两年投入教育经费的年平均增长率为 ,依题意得
答:这两年投入教育经费的年平均增长率为20%。
即
(舍去)
小结:
2、通过本节课的学习大家有什么新的感受?
1、这节课我们复习了什么?
作业:用适当方法解下列方程
(5)
(1)
(2)
(4)
(3)
