苏科版七年级下册数学课件 7.5 多边形的内角和与外角和(28张)
文档属性
| 名称 | 苏科版七年级下册数学课件 7.5 多边形的内角和与外角和(28张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 632.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览




文档简介
美国国防部大楼——五角大楼
看一看
看一看
7.5多边形的内角和与外角和(2)
-----探索多边形的内角和
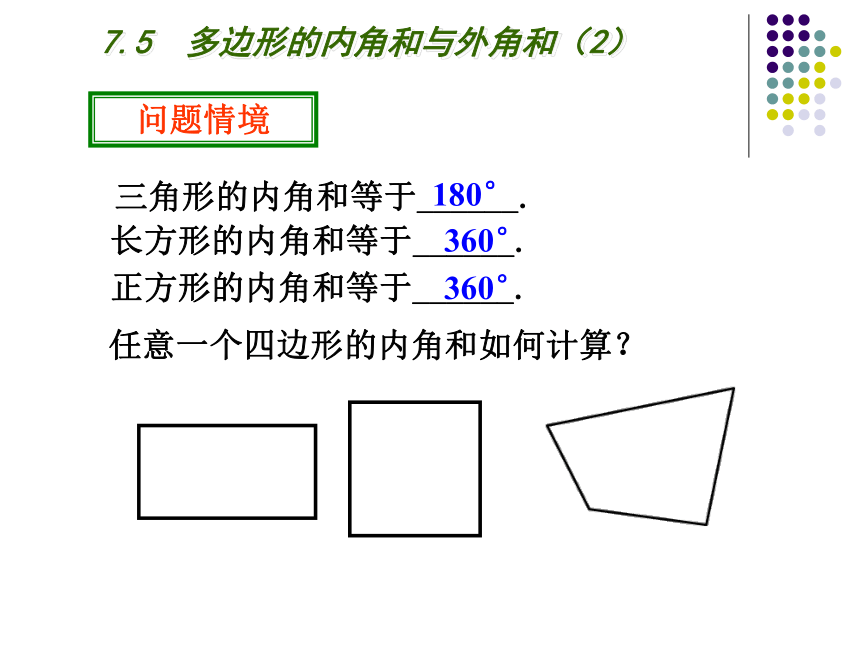
三角形的内角和等于______.
180°
问题情境
任意一个四边形的内角和如何计算?
长方形的内角和等于______.
正方形的内角和等于______.
360°
360°
7.5 多边形的内角和与外角和(2)
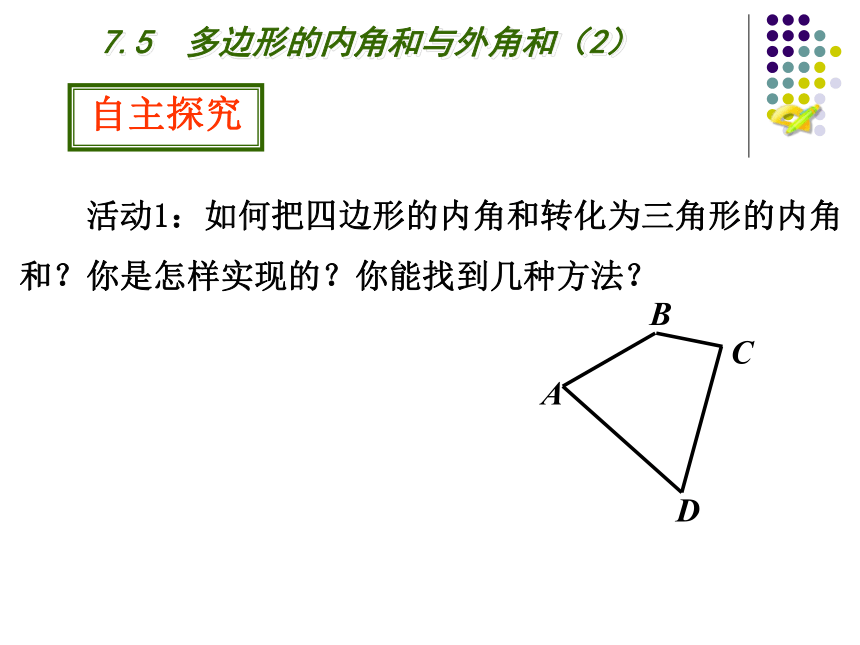
自主探究
活动1:如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?你能找到几种方法?
D
C
B
A
7.5 多边形的内角和与外角和(2)
D
C
B
A
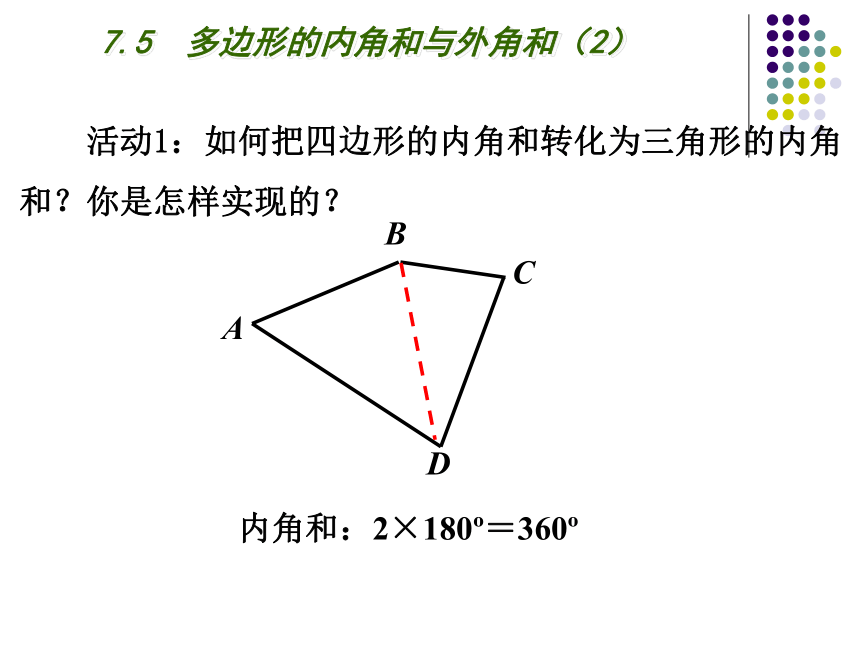
内角和:2×180?=360?
活动1:如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?
7.5 多边形的内角和与外角和(2)
A
C
D
B
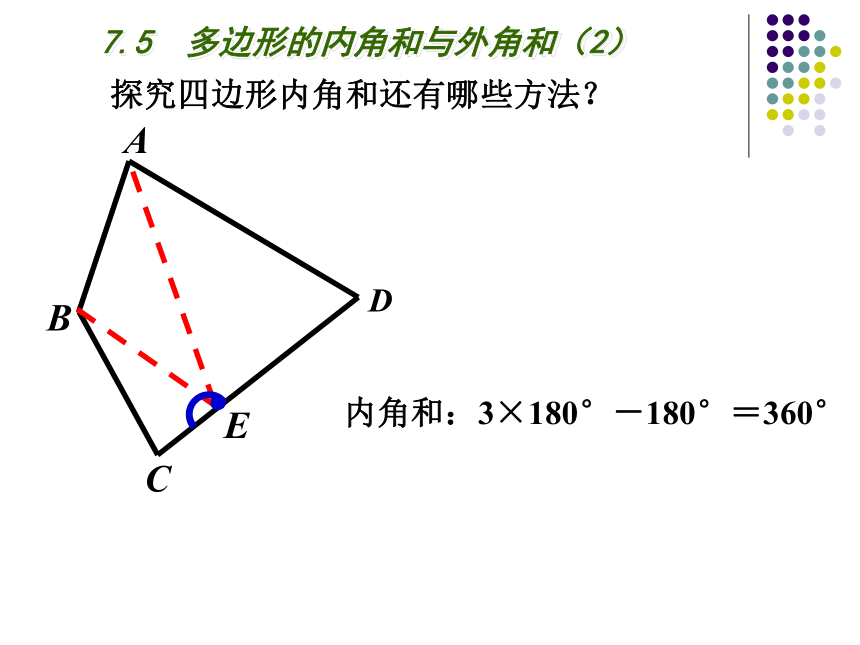
内角和:3×180°-180°=360°
.
E
⌒
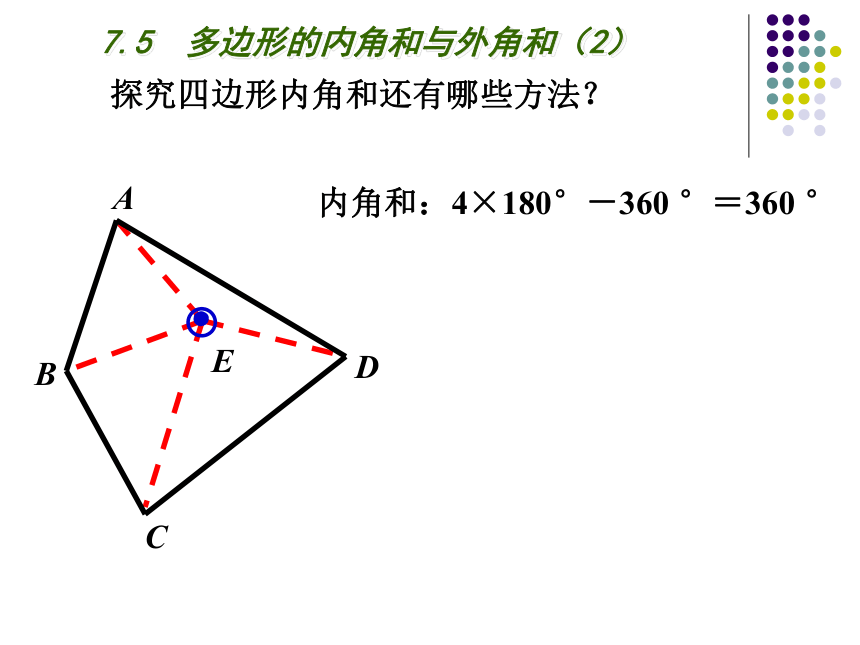
探究四边形内角和还有哪些方法?
7.5 多边形的内角和与外角和(2)
内角和:4×180°-360 °=360 °
D
C
B
A
E
.
探究四边形内角和还有哪些方法?
7.5 多边形的内角和与外角和(2)
A
C
D
B
E
内角和:3×180?-180?=360?
.
探究四边形内角和还有哪些方法?
7.5 多边形的内角和与外角和(2)
A
C
D
B
C
A
D
B
.
O
⌒
A
C
D
B
O
.
把四边形问题转化为熟悉的三角形问题来解决.
D
C
B
A
E
.
7.5 多边形的内角和与外角和(2)
活动2 请你选择其中一种方法探索四边形的内角和.
从四边形的一个顶点出发,可以作_____条对角线,它们将
四边形分为 个三角形,四边形的内角和等于
180°×____= °.
1
2
2
360
A
B
C
D
自主探究
7.5 多边形的内角和与外角和(2)
A
B
C
D
E
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180?× = ?.
2
3
3
540
活动2 请你选择其中一种方法探索五边形的内角和.
自主探究
7.5 多边形的内角和与外角和(2)
如图,从六边形的一个顶点出发,可以作_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于
180°×___=_____°.
3
4
4
720
C
A
B
D
E
F
活动2 请你选择其中一种方法探索六边形的内角和.
自主探究
7.5 多边形的内角和与外角和(2)
从n 边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.
活动2 你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?
自主探究
7.5 多边形的内角和与外角和(2)
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一个顶点引出的对角线条数
图形
边数
······
······
0
3-3 =
4-3 =
5-3 =
6-3 =
n-3
1
2
3
3-2 =
1
4-2 =
2
5-2 =
3
6-2 =
4
n-2
( n-2 )·180?
180?
360?
540?
720?
······
······
······
归纳总结
7.5 多边形的内角和与外角和(2)
活动3
正多边形的特点:所有边都相等,所有角都相等;
正多边形的内角和:(n-2)×180?;
正多边形每个内角的度数:(n-2)·180?÷n.
自主探究
7.5 多边形的内角和与外角和(2)
判断:1.四个角都是直角的四边形是正四边形吗?
2.四条边都相等的四边形是正四边形吗?
巩固新知
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补.
7.5 多边形的内角和与外角和(2)
(1)八边形内角和是____?;
(2)十六边形内角和是______?;
(3)如果一个多边形的边数增加1,那么这时它的内角和增加了___度.
练习1
巩固新知
7.5 多边形的内角和与外角和(2)
一个多边形的内角和等于1440°,它是几边形?
练习2
巩固新知
7.5 多边形的内角和与外角和(2)
解:由多边形的内角和公式可得
(n - 2)· 1800 = 14400
(n - 2) = 8
n = 10
∴这是十边形。
练习3 求图中x的值.
巩固新知
7.5 多边形的内角和与外角和(2)
巩固新知
7.5 多边形的内角和与外角和(2)
练习4.每个内角都为1200的多边形是__边形.
小结反思
这节课我收获的知识是?
我学到的一种方法是?
我将进一步研究的问题是?
请用一句话总结:
7.5 多边形的内角和与外角和(2)
课堂练习
1.已知四边形的四个内角的度数的比为1:2:3:4,求这个四边形最大的角的度数.
解:设每份为x,则四个角表示为x,2x,3x,4x,由题意得:
x+2x+3x+4x =(4-2)×1800
解得 x=360
最大的角为 4×360 =1440
2、一个多边形的内角和为1080°,
这个多边形是几边形?
解:设这个多边形为n边形,由题意可得:
180×(n-2)=1080
解得 : n=8
答:这个多边形为8边形.
练一练
3、一个多边形除一个内角外,其余各内角的和为2220°,求这个内角的度数以及这个多边形的边数。
分析:由于多边形的内角和为1800的整数倍,所以用22200÷1800=12.333…,故该多边形的边数应该是13.
一个多边形的所有内角与它的一个外角的和等于2000°,求这个内角的度数以及这个多边形的边数。
练一练
4、在四边形ABCD中,∠A=120度,
∠B:∠C:∠D =3:4:5,
求∠B,∠C,∠D的度数。
看一看
看一看
7.5多边形的内角和与外角和(2)
-----探索多边形的内角和
三角形的内角和等于______.
180°
问题情境
任意一个四边形的内角和如何计算?
长方形的内角和等于______.
正方形的内角和等于______.
360°
360°
7.5 多边形的内角和与外角和(2)
自主探究
活动1:如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?你能找到几种方法?
D
C
B
A
7.5 多边形的内角和与外角和(2)
D
C
B
A
内角和:2×180?=360?
活动1:如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?
7.5 多边形的内角和与外角和(2)
A
C
D
B
内角和:3×180°-180°=360°
.
E
⌒
探究四边形内角和还有哪些方法?
7.5 多边形的内角和与外角和(2)
内角和:4×180°-360 °=360 °
D
C
B
A
E
.
探究四边形内角和还有哪些方法?
7.5 多边形的内角和与外角和(2)
A
C
D
B
E
内角和:3×180?-180?=360?
.
探究四边形内角和还有哪些方法?
7.5 多边形的内角和与外角和(2)
A
C
D
B
C
A
D
B
.
O
⌒
A
C
D
B
O
.
把四边形问题转化为熟悉的三角形问题来解决.
D
C
B
A
E
.
7.5 多边形的内角和与外角和(2)
活动2 请你选择其中一种方法探索四边形的内角和.
从四边形的一个顶点出发,可以作_____条对角线,它们将
四边形分为 个三角形,四边形的内角和等于
180°×____= °.
1
2
2
360
A
B
C
D
自主探究
7.5 多边形的内角和与外角和(2)
A
B
C
D
E
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180?× = ?.
2
3
3
540
活动2 请你选择其中一种方法探索五边形的内角和.
自主探究
7.5 多边形的内角和与外角和(2)
如图,从六边形的一个顶点出发,可以作_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于
180°×___=_____°.
3
4
4
720
C
A
B
D
E
F
活动2 请你选择其中一种方法探索六边形的内角和.
自主探究
7.5 多边形的内角和与外角和(2)
从n 边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.
活动2 你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?
自主探究
7.5 多边形的内角和与外角和(2)
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一个顶点引出的对角线条数
图形
边数
······
······
0
3-3 =
4-3 =
5-3 =
6-3 =
n-3
1
2
3
3-2 =
1
4-2 =
2
5-2 =
3
6-2 =
4
n-2
( n-2 )·180?
180?
360?
540?
720?
······
······
······
归纳总结
7.5 多边形的内角和与外角和(2)
活动3
正多边形的特点:所有边都相等,所有角都相等;
正多边形的内角和:(n-2)×180?;
正多边形每个内角的度数:(n-2)·180?÷n.
自主探究
7.5 多边形的内角和与外角和(2)
判断:1.四个角都是直角的四边形是正四边形吗?
2.四条边都相等的四边形是正四边形吗?
巩固新知
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补.
7.5 多边形的内角和与外角和(2)
(1)八边形内角和是____?;
(2)十六边形内角和是______?;
(3)如果一个多边形的边数增加1,那么这时它的内角和增加了___度.
练习1
巩固新知
7.5 多边形的内角和与外角和(2)
一个多边形的内角和等于1440°,它是几边形?
练习2
巩固新知
7.5 多边形的内角和与外角和(2)
解:由多边形的内角和公式可得
(n - 2)· 1800 = 14400
(n - 2) = 8
n = 10
∴这是十边形。
练习3 求图中x的值.
巩固新知
7.5 多边形的内角和与外角和(2)
巩固新知
7.5 多边形的内角和与外角和(2)
练习4.每个内角都为1200的多边形是__边形.
小结反思
这节课我收获的知识是?
我学到的一种方法是?
我将进一步研究的问题是?
请用一句话总结:
7.5 多边形的内角和与外角和(2)
课堂练习
1.已知四边形的四个内角的度数的比为1:2:3:4,求这个四边形最大的角的度数.
解:设每份为x,则四个角表示为x,2x,3x,4x,由题意得:
x+2x+3x+4x =(4-2)×1800
解得 x=360
最大的角为 4×360 =1440
2、一个多边形的内角和为1080°,
这个多边形是几边形?
解:设这个多边形为n边形,由题意可得:
180×(n-2)=1080
解得 : n=8
答:这个多边形为8边形.
练一练
3、一个多边形除一个内角外,其余各内角的和为2220°,求这个内角的度数以及这个多边形的边数。
分析:由于多边形的内角和为1800的整数倍,所以用22200÷1800=12.333…,故该多边形的边数应该是13.
一个多边形的所有内角与它的一个外角的和等于2000°,求这个内角的度数以及这个多边形的边数。
练一练
4、在四边形ABCD中,∠A=120度,
∠B:∠C:∠D =3:4:5,
求∠B,∠C,∠D的度数。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
