江西省景德镇十六中汤瑛余角和补角
文档属性
| 名称 | 江西省景德镇十六中汤瑛余角和补角 |

|
|
| 格式 | zip | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-20 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
江西景德镇市十六中学 汤瑛
生活中处处可见道路、房屋、山川、桥梁。在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线。在这一章里,我们将发现相交线和平行线的一些特征,并探索两条直线平行的条件。我们还将利用圆规和没有刻度的直尺,尝试着作一些美丽的图案!
玉田水库大坝要修复加固,施工前要求先测
大坝的倾斜角,坝底是石块堆积而成,量角器无法伸入大坝底部测量,聪明的你有什么简单的方法?
1
β
α
α
β
江西景德镇市十六中学 汤瑛
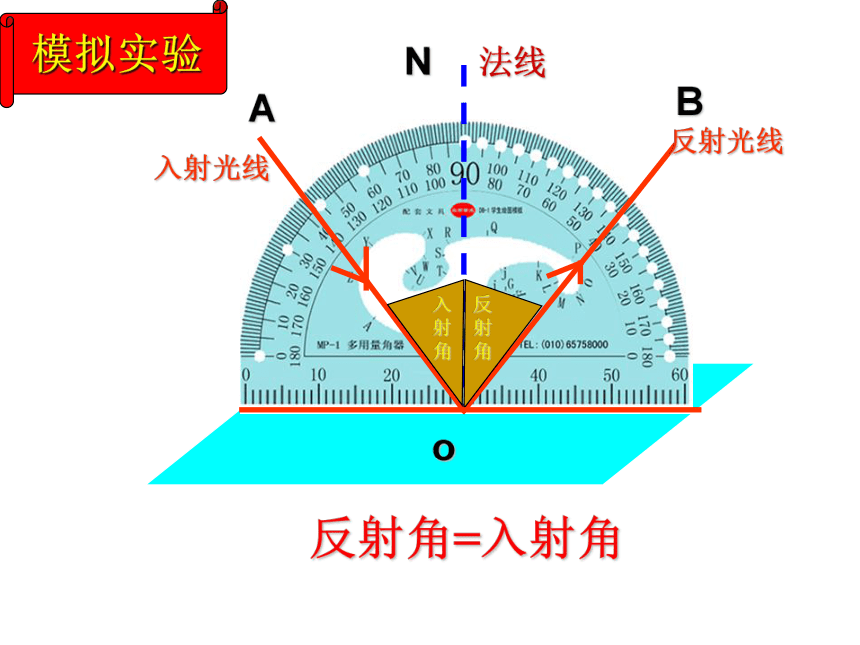
反射角=入射角
入射角
反射角
入射光线
反射光线
法线
模拟实验
A
B
N
o
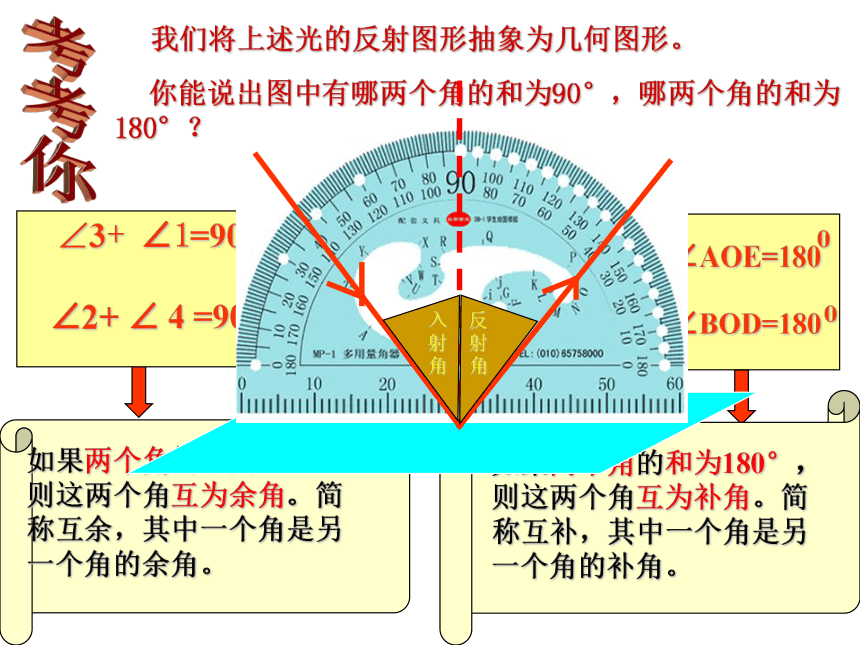
我们将上述光的反射图形抽象为几何图形。
你能说出图中有哪两个角的和为90°,哪两个角的和为180°?
如果两个角的和为90°,则这两个角互为余角。简称互余,其中一个角是另一个角的余角。
如果两个角的和为180°,则这两个角互为补角。简称互补,其中一个角是另一个角的补角。
∠3+ ∠1=90
∠2+ ∠ 4 =90
0
0
∠3+ ∠AOE=180
∠4+ ∠BOD=180
0
0
1
4
2
B
3
A
N
O
D
E
入射角
反射角
(1)30 ,70 与80 的和为平角,所以这三个角互补( )
(2)互余的两个角都是锐角。 ( )
(3)一个角的补角必为钝角。 ( )
(4)90 的角为余角。 ( )
(5)两角是否互补既与其大小有关又与其位置有关( )
0
×
√
×
×
×
互余与互补是指两个角之间的数量关系,与它们的位置关系无关。
判断下列说法是否正确
0
0
0
前后呼应 :测量大坝的倾斜角(即图中的∠1),你有什么简单的方法呢?
1
2
1
方法一:测量∠ 1的补角∠2
方法二:测量∠1的余角∠3
3
2
(
(2)图中∠α的余角∠1,∠2的大小有什么关系?为什么?
(3) 这一结论用文字怎么叙述?
同 角的余角相等
A
(或等)
α
2
β
1
1
又因为∠α=∠β
(1) 动手画一画: 已知∠α(如图),请利用三角板画∠α的余角
C
O
B
α
(
D
探究乐园一
同 角的补角相等
(或等)
C
O
B
α
1
A
D
2
α
β
1
2
(2) 动手画一画
已知∠α(如图),请利用三角板画∠α的补角
图中∠α的补角∠1,∠2的大小有什么关系?为什么?
探究乐园二
探究乐园三
1
2
A
D
C
B
O
图中,还有相等的角吗?这几组相等的角在位置上有什么样的关系,你能试着描述一下吗?
像∠ 1与∠2, ∠ AOC与∠BOD一样,两个角有公共的顶点O,且一个角的两边是另一角两边的反向延长线,这两个角互为对顶角。
我发现了
对顶角相等
定义:
性质:
1.下图中有对顶角吗?若有,请指出,若没有,请说明理由
小试牛刀
对顶角要满足两个条件:
1、两个角有公共顶点;
2、角的两边互为反向延长线
(1)因为∠ 1与∠2无公共顶点,所以它们不是对顶角;
(2)因为∠2的两边并不都是∠ 1两边的反向延长线,
所以不是对顶角;
(3)符合对顶角的定义,所以它们是对顶角。
如图所示,有一个破损的扇形零件,利用量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角是多少度吗?你的根据是什么?
40
0
方法一:可利用对顶角相等得出。
方法二:可利用补角得出。
学以致用
用方程的思想解决几何问题是常用的一种数学方法。
若一个角的补角等于它的余角的4倍,求
这个角的度数。
解:设这个角是x ,则它的补角是(180-x)°,
余角是(90-x) °,根据题意得:
180-x = 4 (90-x)
解得: x =60
答:这个角的度数是60 °。
如图:∠ACB=90°, CD垂直AB于点D,∠A与∠BCD有什么大小关系?为什么?
答:∠A=∠BCD
因为∠A+∠B=90° ∠BCD+∠B=90°
所以∠A=∠BCD
(同角的余角相等)
拓展
理一理 今天学习的知识
余角、补角、对顶角的概念:
(1) 和为直角的两个角称互为余角;
(2) 和为平角的两个角称互为补角;
(3) 有公共顶点,且两个角的两边互为反向延长线的两个角互为对顶角。
余角、补角、对顶角的性质:
(1) 同角或等角的余角相等;
(2) 同角或等角的补角相等;
(3) 对顶角相等。
互余与互补只与角的数量有关,与位置无关。而对顶角是根据角的位置来判断的
作业
1. 习题2.1 数学理解1
2. 习题2.1 问题解决1,2
江西景德镇市十六中学 汤瑛
生活中处处可见道路、房屋、山川、桥梁。在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线。在这一章里,我们将发现相交线和平行线的一些特征,并探索两条直线平行的条件。我们还将利用圆规和没有刻度的直尺,尝试着作一些美丽的图案!
玉田水库大坝要修复加固,施工前要求先测
大坝的倾斜角,坝底是石块堆积而成,量角器无法伸入大坝底部测量,聪明的你有什么简单的方法?
1
β
α
α
β
江西景德镇市十六中学 汤瑛
反射角=入射角
入射角
反射角
入射光线
反射光线
法线
模拟实验
A
B
N
o
我们将上述光的反射图形抽象为几何图形。
你能说出图中有哪两个角的和为90°,哪两个角的和为180°?
如果两个角的和为90°,则这两个角互为余角。简称互余,其中一个角是另一个角的余角。
如果两个角的和为180°,则这两个角互为补角。简称互补,其中一个角是另一个角的补角。
∠3+ ∠1=90
∠2+ ∠ 4 =90
0
0
∠3+ ∠AOE=180
∠4+ ∠BOD=180
0
0
1
4
2
B
3
A
N
O
D
E
入射角
反射角
(1)30 ,70 与80 的和为平角,所以这三个角互补( )
(2)互余的两个角都是锐角。 ( )
(3)一个角的补角必为钝角。 ( )
(4)90 的角为余角。 ( )
(5)两角是否互补既与其大小有关又与其位置有关( )
0
×
√
×
×
×
互余与互补是指两个角之间的数量关系,与它们的位置关系无关。
判断下列说法是否正确
0
0
0
前后呼应 :测量大坝的倾斜角(即图中的∠1),你有什么简单的方法呢?
1
2
1
方法一:测量∠ 1的补角∠2
方法二:测量∠1的余角∠3
3
2
(
(2)图中∠α的余角∠1,∠2的大小有什么关系?为什么?
(3) 这一结论用文字怎么叙述?
同 角的余角相等
A
(或等)
α
2
β
1
1
又因为∠α=∠β
(1) 动手画一画: 已知∠α(如图),请利用三角板画∠α的余角
C
O
B
α
(
D
探究乐园一
同 角的补角相等
(或等)
C
O
B
α
1
A
D
2
α
β
1
2
(2) 动手画一画
已知∠α(如图),请利用三角板画∠α的补角
图中∠α的补角∠1,∠2的大小有什么关系?为什么?
探究乐园二
探究乐园三
1
2
A
D
C
B
O
图中,还有相等的角吗?这几组相等的角在位置上有什么样的关系,你能试着描述一下吗?
像∠ 1与∠2, ∠ AOC与∠BOD一样,两个角有公共的顶点O,且一个角的两边是另一角两边的反向延长线,这两个角互为对顶角。
我发现了
对顶角相等
定义:
性质:
1.下图中有对顶角吗?若有,请指出,若没有,请说明理由
小试牛刀
对顶角要满足两个条件:
1、两个角有公共顶点;
2、角的两边互为反向延长线
(1)因为∠ 1与∠2无公共顶点,所以它们不是对顶角;
(2)因为∠2的两边并不都是∠ 1两边的反向延长线,
所以不是对顶角;
(3)符合对顶角的定义,所以它们是对顶角。
如图所示,有一个破损的扇形零件,利用量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角是多少度吗?你的根据是什么?
40
0
方法一:可利用对顶角相等得出。
方法二:可利用补角得出。
学以致用
用方程的思想解决几何问题是常用的一种数学方法。
若一个角的补角等于它的余角的4倍,求
这个角的度数。
解:设这个角是x ,则它的补角是(180-x)°,
余角是(90-x) °,根据题意得:
180-x = 4 (90-x)
解得: x =60
答:这个角的度数是60 °。
如图:∠ACB=90°, CD垂直AB于点D,∠A与∠BCD有什么大小关系?为什么?
答:∠A=∠BCD
因为∠A+∠B=90° ∠BCD+∠B=90°
所以∠A=∠BCD
(同角的余角相等)
拓展
理一理 今天学习的知识
余角、补角、对顶角的概念:
(1) 和为直角的两个角称互为余角;
(2) 和为平角的两个角称互为补角;
(3) 有公共顶点,且两个角的两边互为反向延长线的两个角互为对顶角。
余角、补角、对顶角的性质:
(1) 同角或等角的余角相等;
(2) 同角或等角的补角相等;
(3) 对顶角相等。
互余与互补只与角的数量有关,与位置无关。而对顶角是根据角的位置来判断的
作业
1. 习题2.1 数学理解1
2. 习题2.1 问题解决1,2
