湘教版八年级下学期复习专题1 直角三角形的性质(含解析)
文档属性
| 名称 | 湘教版八年级下学期复习专题1 直角三角形的性质(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 15:00:45 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下学期复习专题1
直角三角形的性质
一、单选题
1.满足下列条件的三角形中,不是直角三角形的是(???
)
A.?∠A-∠B=∠C???????????B.?∠A:∠B:∠C=3:4:7???????????C.?∠A=2∠B=3∠C???????????D.?∠A=9°,∠B=81°
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(???
)
A.?锐角三角形????????????????????????B.?钝角三角形????????????????????????C.?直角三角形????????????????????????D.?都有可能
3.如图由于台风的影响,一棵树在离地面
处折断,折断后树干上部分与地面成30度的夹角,折断前长度是?
(?????????
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
.
4.如右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,DE的长为(??
)
A.?7.4m??????????????????????????????????B.?3.7m??????????????????????????????????C.?1.85m??????????????????????????????????D.?2.85m
5.将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为h,则h的取值范围是(
??)
A.?12cm≤h≤19cm?????????????B.?12cm≤h≤13cm?????????????C.?11cm≤h≤12cm?????????????D.?5cm≤h≤12cm
6.如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是5,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是(??
)
A.?4??????????????????????????????????????????B.?9??????????????????????????????????????????C.?16??????????????????????????????????????????D.?25
7.若一个三角形三边满足(a+b)2﹣c2=2ab,则这个三角形是(??
)
A.?直角三角形??????????????????B.?等腰直角三角形??????????????????C.?等腰三角形??????????????????D.?以上结论都不对
8.下列各组数中,是勾股数的是(???
)
A.?0.3,0.4,0.5??????????????????B.?
,
,
??????????????????C.?6,8,10??????????????????D.?1.5,2,2.5
9.我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a
,
较长直角边长为b
,
那么(a+b)2的值为( )
A.?13????????????????????????????????????????B.?19????????????????????????????????????????C.?25????????????????????????????????????????D.?169
10.如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则
BC
的长是(???
)
A.?8?????????????????????????????????????????B.?10?????????????????????????????????????????C.?12?????????????????????????????????????????D.?16
11.已知Rt△ABC中,∠C=90°,若a+b=10cm,c=8cm,则Rt△ABC的面积为(???
)
A.?9cm2????????????????????????????????B.?18cm2????????????????????????????????C.?24cm?????????????????????????????????D.?36cm2
12.将一根长为25厘米的筷子至于底面直径为5厘米,高为12厘米的圆柱形水杯中,设筷子漏在杯子外的长为h厘米,则h的取值范围是(
???)
A.?12≤h≤13??????????????????????????B.?11≤h≤12??????????????????????????C.?11≤h≤13??????????????????????????D.?10≤h≤12
二、填空题
13.在Rt
ABC中,∠C=90°,∠A=65°,则∠B=________.
14.如图,Rt△ABC中,∠ACB=90°,D为斜边AB的中点,AB=6cm,则CD的长为________cm.
15.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的高,若AB=8,则BD=________.
16.如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,则AD的取值范围是________.
17.如图,作一个长方形,以数轴的原点为中心,长方形对角线为半径,交数轴于点A,则点A表示的数是________.
18.如图,将长AB=5cm,宽AD=3cm的矩形纸片ABCD折叠,使点A与C重合,折痕为EF,则AE长为________cm.
三、计算题
19.在
Rt△ABC
中,∠C=90°,∠A、∠B、∠C
的对边分别为
a、b、c
.
若
a∶c=15∶17,b=24,求
a.
四、解答题
20.如图,
中,
,CD是
的高,
,
,求BD长.
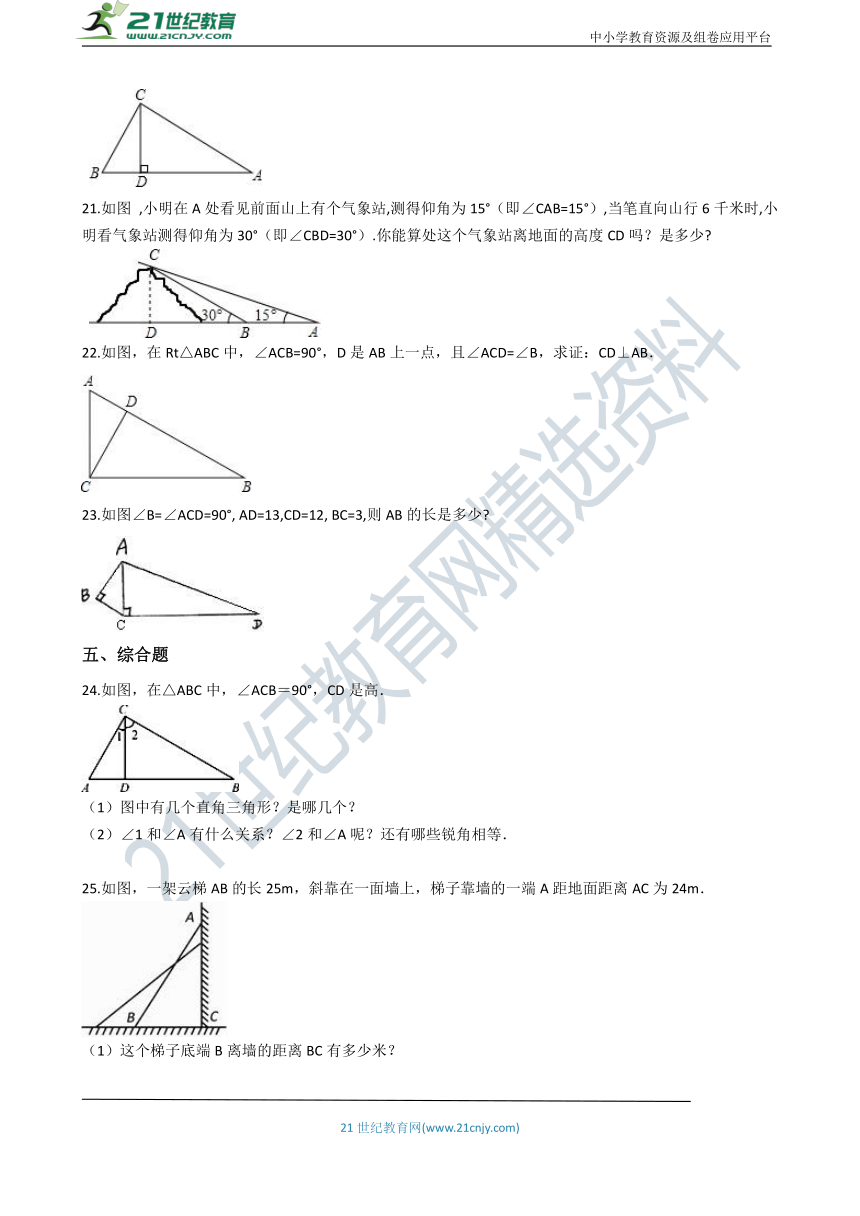
21.如图
,小明在A处看见前面山上有个气象站,测得仰角为15°(即∠CAB=15°),当笔直向山行6千米时,小明看气象站测得仰角为30°(即∠CBD=30°).你能算处这个气象站离地面的高度CD吗?是多少?
22.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
23.如图∠B=∠ACD=90°,
AD=13,CD=12,
BC=3,则AB的长是多少?
?
五、综合题
24.如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
25.如图,一架云梯AB的长25m,斜靠在一面墙上,梯子靠墙的一端A距地面距离AC为24m.
(1)这个梯子底端B离墙的距离BC有多少米?
(2)如果梯子的顶端下滑了4m,那么梯子的底部在水平方向也滑动了4
m吗?为什么?
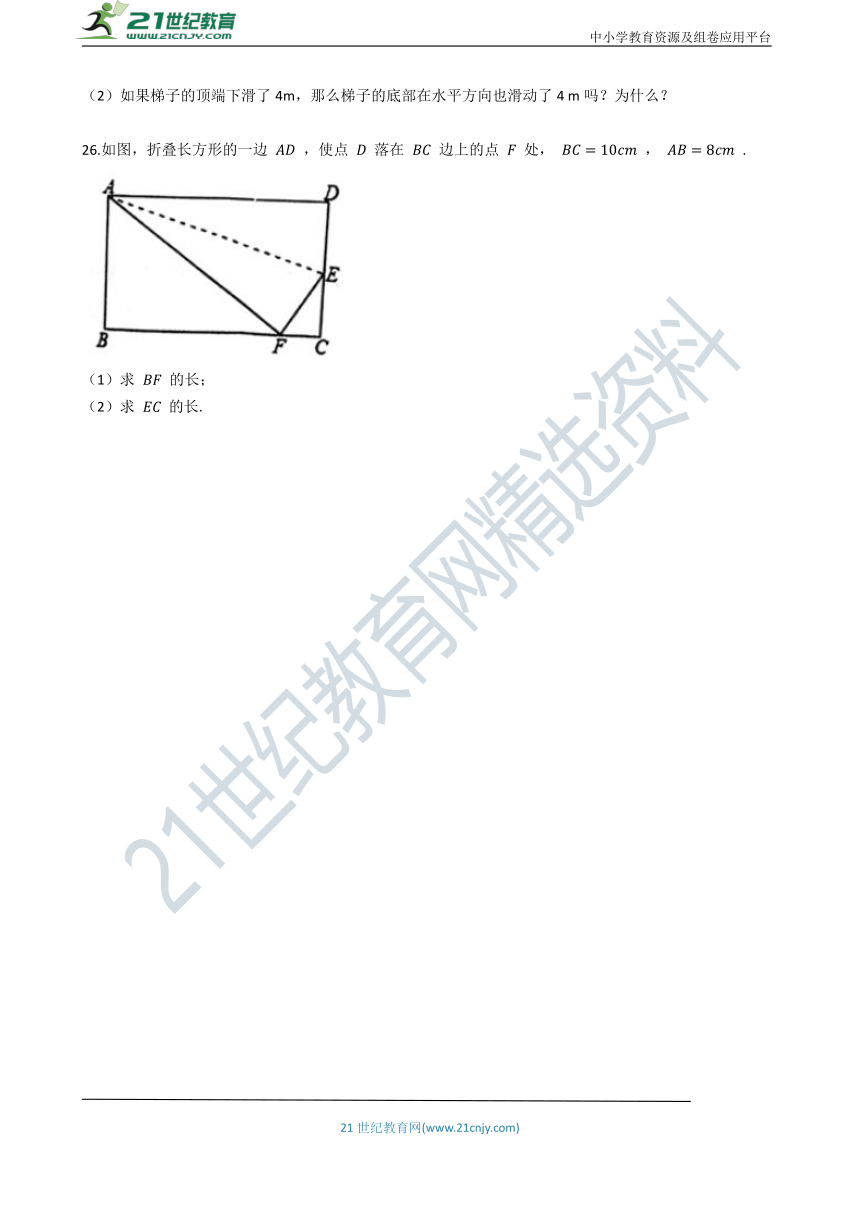
26.如图,折叠长方形的一边
,使点
落在
边上的点
处,
,
.
(1)求
的长;
(2)求
的长.
答案解析部分
一、单选题
1.【答案】
C
解:A.∵∠A-∠B=∠C,∴∠A=∠B+∠C=90°,∴该三角形是直角三角形;
B.∵∠A:∠B:∠C=3:4:7,∴∠C=180°×
=90°,∴该三角形是直角三角形;
C.∵∠A=2∠B=3∠C,∴∠A=180°×
>90°,∴该三角形是钝角三角形;
D.∵∠A=9°,∠B=81°,∴∠C=90°,∴该三角形是直角三角形;
故答案为:C.
2.【答案】
C
解:∵三角形三条高的交点恰好为三角形的顶点
∴该三角形为直角三角形
故答案为:C。
3.【答案】
C
解:如图,
∵∠BAC=30°,∠BCA=90°,
∴AB=2CB,
而BC=3米,
∴AB=6米,
∴这棵大树在折断前的高度为AB+BC=9米.
故答案为:C.
4.【答案】
C
解:在直角三角形ADE中,∵∠A=30°,AB=7.4,D为AB的中点
∴DE=AD==1.85.
故答案为:C。
5.【答案】
C
解:
h最大时为筷子与杯底垂直时,h=12cm
最小时为筷子与杯底和杯高形成直角三角形时,AB=
h=24-13=11cm,
∴11cm≤h≤12cm.
故答案为:C.
6.【答案】
B
解:∵大正方形的面积是5,
∴c2=5,
∴a2+b2=c2=5,
∵直角三角形的面积是
=1,
又∵直角三角形的面积是
ab=1,
∴ab=2,
∴(a+b)2=a2+b2+2ab=c2+2ab=5+2×2=5+4=9.
故选:B.
7.【答案】
A
解:∵(a+b)2﹣c2=2ab,
∴a2+b2+2ab﹣c2=2ab,
∴a2+b2=c2
,
∴这个三角形为直角三角形.
故答案为:A.
8.【答案】
C
解:A.因为0.32+0.42=0.52
,
0.3,0.4,0.5能组成直角三角形,但0.3,0.4,0.5不是正整数,所以0.3,0.4,0.5不是勾股数,故A错误;
B.因为()2+()2
=()2
,
,
,
能组成直角三角形,但
,
,
不是正整数,所以
,
,
不是勾股数,故B错误;
C.因为62+82=102
,
所以正整数6,8,10能组成直角三角形,所以6,8,10是勾股数,故C正确;
D.因为1.52+22=2.52
,
1.5,2,2.5能组成直角三角形,但1.5,2,2.5不是正整数,所以1.5,2,2.5不是勾股数,故D错误.
故答案为:C.
9.【答案】
C
解:小正方形面积开方,得边长1,则有b-a=1
大正方形边长的平方为其面积即13,则在三角形中有
=13
将b-a=1两边平方,得
=1
将
=13代入,得13-2ab=1
故ab=6
由
=13与2ab=12两式相加,得
故答案为:C
10.【答案】
C
解:在△ACD中,AD⊥CD,
∴∠D=90°,
∵CD=4,AD=3,
∴由勾股定理得:AC=,
在△ABC中,∠ACB=90°,AB=13,
∴由勾股定理得:BC=。
11.【答案】
A
解:∵Rt△ABC中,∠C=90°,c=8,
∴a2+b2=c2=64,
∴(a+b)2-2ab=64
∴100-2ab=64
解之:ab=18.
∴S△ABC=ab=9.
故答案为:A.
12.【答案】
A
解:如图,
由题意可知AB=5cm,AE=BD=25cm,BC=12cm
∴CD=h=25-12=13,
AC=
∴CE=h=AE-AC=25-13=12
∴h的取值范围是:12≤h≤13.
故答案为:A
二、填空题
13.【答案】
25°
解:如图,在直角三角形ABC中,∠C=90°,∠A=65°,
则∠B=90°-∠A=25°(直角三角形中,两个锐角互余).
故答案是:25°.
14.【答案】
3
解:在Rt△ABC中,
∵∠ACB-90°,AB=6cm,D为斜边AB的中点,
∴CD=AB=3(cm).
故答案为:3.
15.【答案】
2
解:由题,
在Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,
∴
BC=
AB=4,
∵CD是斜边AB上的高,
∴∠ADC=∠BDC=90°,
∴∠ACD=60°,
∴∠DCB=30°,
在Rt△BDC中,∠DCB=30°,
∴BD=
BC=2.
故答案为:2.
16.【答案】
2<AD<8
解:如图,延长BC交AD的延长线于E,作BF⊥AD于F,
在Rt△ABE中,∵∠E=30°,AB=4,
∴AE=2AB=8,
在Rt△ABF中,AF=
AB=2,
∴AD的取值范围为2<AD<8,
故答案为:2<AD<8
17.【答案】
解:长方形的对角线长==
,
????????????
又∵点A在数轴的负半轴,∴点A表示的数是.
????????????
故答案为:.
18.【答案】
3.4
解:根据矩形的性质可得:BC=AD=3cm,设AE=xcm,则BE=(5-x)cm,根据折叠图形的性质可得CE=AE=xcm,根据Rt△BCE的勾股定理可得:
,解得:x=3.4
三、计算题
19.【答案】
解:设a=15x,则c=17x,
由勾股定理得,(15x)2+242=(17x)2
,
解得,x=3,
则a=15x=45.
四、解答题
20.【答案】
解:
中,
,
,
,
,
是
的高,
,
,
故
,
在
中,
,
.
21.【答案】
解:∵∠A=15°,∠CBD=30°,
∴∠ACB=∠A=15°,
∴BC=AB=6千米
在直角△BCD中,则CD=
BC=3千米.
22.【答案】
证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB
23.【答案】
解:
∵∠ACD=90°
AD=13,
CD=12
∴AC2
=AD2-CD2
=132-122
=25
∴AC=5
又∵∠ABC=90°且BC=3
∴由勾股定理可得
AB2=AC2-BC2
=52-32
=16
∴AB=
4
∴AB的长是4.
五、综合题
24.【答案】
(1)解:
?∠ACB=90°,CD是高,∴∠ADC=∠BDC=∠ACB=90°∴图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
(2)解:∠1+∠A=90°,∠2=∠A,∠1=∠B.
??ACD,△BCD,△ABC是直角三角形,且∠ADC、∠BDC、∠ACB是直角,∴∠1+∠A=90°,∠1+∠2=90°,∠B+∠A=90°∴∠2=∠A,∠1=∠B
25.【答案】
(1)解:由题意得此时AC=24米,AB=25米,根据AC2+BC2=AB2
,
可得:BC=7,
答:这个梯子底端离墙有7米;
(2)解:不是.
理由:设滑动后梯子的底端到墙的距离为x米,
得方程,x2+(24?4)2=252
,
解得:x=15,
所以梯子向后滑动了8米.
26.【答案】
(1)解:由题意可得,
在
中,∵
,
∴
(2)解:∵
由题意可得
,设
的长为
cm
则在
中,
解得
则
的长为
.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下学期复习专题1
直角三角形的性质
一、单选题
1.满足下列条件的三角形中,不是直角三角形的是(???
)
A.?∠A-∠B=∠C???????????B.?∠A:∠B:∠C=3:4:7???????????C.?∠A=2∠B=3∠C???????????D.?∠A=9°,∠B=81°
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(???
)
A.?锐角三角形????????????????????????B.?钝角三角形????????????????????????C.?直角三角形????????????????????????D.?都有可能
3.如图由于台风的影响,一棵树在离地面
处折断,折断后树干上部分与地面成30度的夹角,折断前长度是?
(?????????
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
.
4.如右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,DE的长为(??
)
A.?7.4m??????????????????????????????????B.?3.7m??????????????????????????????????C.?1.85m??????????????????????????????????D.?2.85m
5.将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为h,则h的取值范围是(
??)
A.?12cm≤h≤19cm?????????????B.?12cm≤h≤13cm?????????????C.?11cm≤h≤12cm?????????????D.?5cm≤h≤12cm
6.如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是5,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是(??
)
A.?4??????????????????????????????????????????B.?9??????????????????????????????????????????C.?16??????????????????????????????????????????D.?25
7.若一个三角形三边满足(a+b)2﹣c2=2ab,则这个三角形是(??
)
A.?直角三角形??????????????????B.?等腰直角三角形??????????????????C.?等腰三角形??????????????????D.?以上结论都不对
8.下列各组数中,是勾股数的是(???
)
A.?0.3,0.4,0.5??????????????????B.?
,
,
??????????????????C.?6,8,10??????????????????D.?1.5,2,2.5
9.我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a
,
较长直角边长为b
,
那么(a+b)2的值为( )
A.?13????????????????????????????????????????B.?19????????????????????????????????????????C.?25????????????????????????????????????????D.?169
10.如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则
BC
的长是(???
)
A.?8?????????????????????????????????????????B.?10?????????????????????????????????????????C.?12?????????????????????????????????????????D.?16
11.已知Rt△ABC中,∠C=90°,若a+b=10cm,c=8cm,则Rt△ABC的面积为(???
)
A.?9cm2????????????????????????????????B.?18cm2????????????????????????????????C.?24cm?????????????????????????????????D.?36cm2
12.将一根长为25厘米的筷子至于底面直径为5厘米,高为12厘米的圆柱形水杯中,设筷子漏在杯子外的长为h厘米,则h的取值范围是(
???)
A.?12≤h≤13??????????????????????????B.?11≤h≤12??????????????????????????C.?11≤h≤13??????????????????????????D.?10≤h≤12
二、填空题
13.在Rt
ABC中,∠C=90°,∠A=65°,则∠B=________.
14.如图,Rt△ABC中,∠ACB=90°,D为斜边AB的中点,AB=6cm,则CD的长为________cm.
15.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的高,若AB=8,则BD=________.
16.如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,则AD的取值范围是________.
17.如图,作一个长方形,以数轴的原点为中心,长方形对角线为半径,交数轴于点A,则点A表示的数是________.
18.如图,将长AB=5cm,宽AD=3cm的矩形纸片ABCD折叠,使点A与C重合,折痕为EF,则AE长为________cm.
三、计算题
19.在
Rt△ABC
中,∠C=90°,∠A、∠B、∠C
的对边分别为
a、b、c
.
若
a∶c=15∶17,b=24,求
a.
四、解答题
20.如图,
中,
,CD是
的高,
,
,求BD长.
21.如图
,小明在A处看见前面山上有个气象站,测得仰角为15°(即∠CAB=15°),当笔直向山行6千米时,小明看气象站测得仰角为30°(即∠CBD=30°).你能算处这个气象站离地面的高度CD吗?是多少?
22.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
23.如图∠B=∠ACD=90°,
AD=13,CD=12,
BC=3,则AB的长是多少?
?
五、综合题
24.如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
25.如图,一架云梯AB的长25m,斜靠在一面墙上,梯子靠墙的一端A距地面距离AC为24m.
(1)这个梯子底端B离墙的距离BC有多少米?
(2)如果梯子的顶端下滑了4m,那么梯子的底部在水平方向也滑动了4
m吗?为什么?
26.如图,折叠长方形的一边
,使点
落在
边上的点
处,
,
.
(1)求
的长;
(2)求
的长.
答案解析部分
一、单选题
1.【答案】
C
解:A.∵∠A-∠B=∠C,∴∠A=∠B+∠C=90°,∴该三角形是直角三角形;
B.∵∠A:∠B:∠C=3:4:7,∴∠C=180°×
=90°,∴该三角形是直角三角形;
C.∵∠A=2∠B=3∠C,∴∠A=180°×
>90°,∴该三角形是钝角三角形;
D.∵∠A=9°,∠B=81°,∴∠C=90°,∴该三角形是直角三角形;
故答案为:C.
2.【答案】
C
解:∵三角形三条高的交点恰好为三角形的顶点
∴该三角形为直角三角形
故答案为:C。
3.【答案】
C
解:如图,
∵∠BAC=30°,∠BCA=90°,
∴AB=2CB,
而BC=3米,
∴AB=6米,
∴这棵大树在折断前的高度为AB+BC=9米.
故答案为:C.
4.【答案】
C
解:在直角三角形ADE中,∵∠A=30°,AB=7.4,D为AB的中点
∴DE=AD==1.85.
故答案为:C。
5.【答案】
C
解:
h最大时为筷子与杯底垂直时,h=12cm
最小时为筷子与杯底和杯高形成直角三角形时,AB=
h=24-13=11cm,
∴11cm≤h≤12cm.
故答案为:C.
6.【答案】
B
解:∵大正方形的面积是5,
∴c2=5,
∴a2+b2=c2=5,
∵直角三角形的面积是
=1,
又∵直角三角形的面积是
ab=1,
∴ab=2,
∴(a+b)2=a2+b2+2ab=c2+2ab=5+2×2=5+4=9.
故选:B.
7.【答案】
A
解:∵(a+b)2﹣c2=2ab,
∴a2+b2+2ab﹣c2=2ab,
∴a2+b2=c2
,
∴这个三角形为直角三角形.
故答案为:A.
8.【答案】
C
解:A.因为0.32+0.42=0.52
,
0.3,0.4,0.5能组成直角三角形,但0.3,0.4,0.5不是正整数,所以0.3,0.4,0.5不是勾股数,故A错误;
B.因为()2+()2
=()2
,
,
,
能组成直角三角形,但
,
,
不是正整数,所以
,
,
不是勾股数,故B错误;
C.因为62+82=102
,
所以正整数6,8,10能组成直角三角形,所以6,8,10是勾股数,故C正确;
D.因为1.52+22=2.52
,
1.5,2,2.5能组成直角三角形,但1.5,2,2.5不是正整数,所以1.5,2,2.5不是勾股数,故D错误.
故答案为:C.
9.【答案】
C
解:小正方形面积开方,得边长1,则有b-a=1
大正方形边长的平方为其面积即13,则在三角形中有
=13
将b-a=1两边平方,得
=1
将
=13代入,得13-2ab=1
故ab=6
由
=13与2ab=12两式相加,得
故答案为:C
10.【答案】
C
解:在△ACD中,AD⊥CD,
∴∠D=90°,
∵CD=4,AD=3,
∴由勾股定理得:AC=,
在△ABC中,∠ACB=90°,AB=13,
∴由勾股定理得:BC=。
11.【答案】
A
解:∵Rt△ABC中,∠C=90°,c=8,
∴a2+b2=c2=64,
∴(a+b)2-2ab=64
∴100-2ab=64
解之:ab=18.
∴S△ABC=ab=9.
故答案为:A.
12.【答案】
A
解:如图,
由题意可知AB=5cm,AE=BD=25cm,BC=12cm
∴CD=h=25-12=13,
AC=
∴CE=h=AE-AC=25-13=12
∴h的取值范围是:12≤h≤13.
故答案为:A
二、填空题
13.【答案】
25°
解:如图,在直角三角形ABC中,∠C=90°,∠A=65°,
则∠B=90°-∠A=25°(直角三角形中,两个锐角互余).
故答案是:25°.
14.【答案】
3
解:在Rt△ABC中,
∵∠ACB-90°,AB=6cm,D为斜边AB的中点,
∴CD=AB=3(cm).
故答案为:3.
15.【答案】
2
解:由题,
在Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,
∴
BC=
AB=4,
∵CD是斜边AB上的高,
∴∠ADC=∠BDC=90°,
∴∠ACD=60°,
∴∠DCB=30°,
在Rt△BDC中,∠DCB=30°,
∴BD=
BC=2.
故答案为:2.
16.【答案】
2<AD<8
解:如图,延长BC交AD的延长线于E,作BF⊥AD于F,
在Rt△ABE中,∵∠E=30°,AB=4,
∴AE=2AB=8,
在Rt△ABF中,AF=
AB=2,
∴AD的取值范围为2<AD<8,
故答案为:2<AD<8
17.【答案】
解:长方形的对角线长==
,
????????????
又∵点A在数轴的负半轴,∴点A表示的数是.
????????????
故答案为:.
18.【答案】
3.4
解:根据矩形的性质可得:BC=AD=3cm,设AE=xcm,则BE=(5-x)cm,根据折叠图形的性质可得CE=AE=xcm,根据Rt△BCE的勾股定理可得:
,解得:x=3.4
三、计算题
19.【答案】
解:设a=15x,则c=17x,
由勾股定理得,(15x)2+242=(17x)2
,
解得,x=3,
则a=15x=45.
四、解答题
20.【答案】
解:
中,
,
,
,
,
是
的高,
,
,
故
,
在
中,
,
.
21.【答案】
解:∵∠A=15°,∠CBD=30°,
∴∠ACB=∠A=15°,
∴BC=AB=6千米
在直角△BCD中,则CD=
BC=3千米.
22.【答案】
证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB
23.【答案】
解:
∵∠ACD=90°
AD=13,
CD=12
∴AC2
=AD2-CD2
=132-122
=25
∴AC=5
又∵∠ABC=90°且BC=3
∴由勾股定理可得
AB2=AC2-BC2
=52-32
=16
∴AB=
4
∴AB的长是4.
五、综合题
24.【答案】
(1)解:
?∠ACB=90°,CD是高,∴∠ADC=∠BDC=∠ACB=90°∴图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
(2)解:∠1+∠A=90°,∠2=∠A,∠1=∠B.
??ACD,△BCD,△ABC是直角三角形,且∠ADC、∠BDC、∠ACB是直角,∴∠1+∠A=90°,∠1+∠2=90°,∠B+∠A=90°∴∠2=∠A,∠1=∠B
25.【答案】
(1)解:由题意得此时AC=24米,AB=25米,根据AC2+BC2=AB2
,
可得:BC=7,
答:这个梯子底端离墙有7米;
(2)解:不是.
理由:设滑动后梯子的底端到墙的距离为x米,
得方程,x2+(24?4)2=252
,
解得:x=15,
所以梯子向后滑动了8米.
26.【答案】
(1)解:由题意可得,
在
中,∵
,
∴
(2)解:∵
由题意可得
,设
的长为
cm
则在
中,
解得
则
的长为
.
21世纪教育网(www.21cnjy.com)
同课章节目录
