连云港市灌南县灌河中学2012届中考数学二轮专题复习一 化归思想问题
文档属性
| 名称 | 连云港市灌南县灌河中学2012届中考数学二轮专题复习一 化归思想问题 |  | |
| 格式 | zip | ||
| 文件大小 | 548.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-20 23:53:07 | ||
图片预览


文档简介
中考数学专题复习一 化归思想问题
一、总体概述
数学思想是数学内容的进一步提炼和概括,是对数学内容的种本质认识,数学方法是实施有关数学思想的一种方式、途径、手段,数学思想方法是数学发现、发明的关键和动力.抓住数学思想方法,善于迅速调用数学思想方法,更是提高解题能力根本之所在.因此,在复习时要注意体会教材例题、习题以及中考试题中所体现的数学思想和方法,培养用数学思想方法解决问题的意识. 初中数学的主要数学思想是化归思想、分类讨论思想、数形结合思想等.本专题专门复习化归思想.所谓化归思想就是化未知为已知、化繁为简、化难为易.如将分式方程化为整式方程,将代数问题化为几何问题,将四边形问题转化为三角形问题等.实现这种转化的方法有:待定系数法、配方法、整体代人法以及化动为静、由抽象到具体等.
二、典型例题
【例题1】如图3-1-1,反比例函数y=-与一次函数y=-x+2的图象交于A、B两点.
(1)求 A、B两点的坐标;
(2)求△AOB的面积.
【例题2】解方程:
【例题3】如图 3-1-2,梯形 ABCD中,AD∥BC,AB=CD,对角线AC、BD相交于O点,且AC⊥BD,AD=3,BC=5,求AC的长.
【例题4】已知△ABC的三边为a,b,c,且,试判断△ABC的形状.
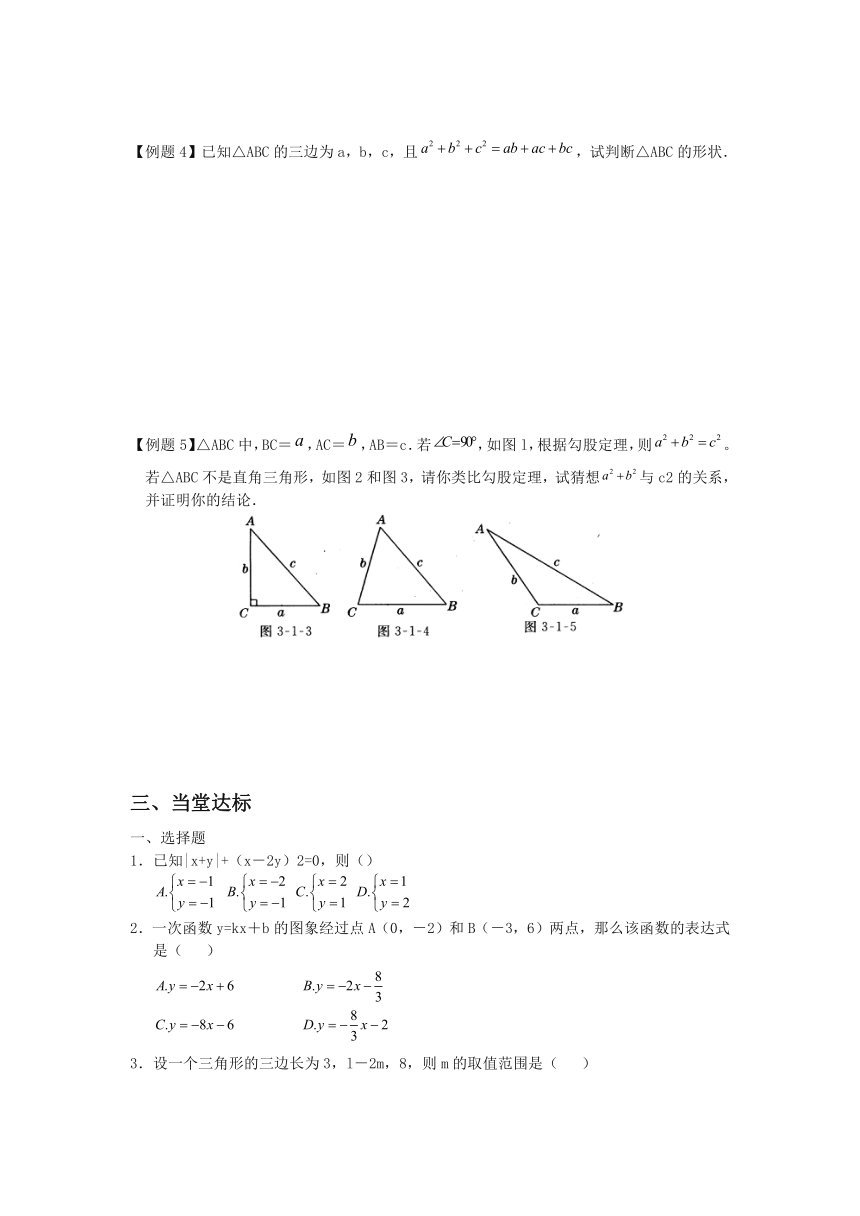
【例题5】△ABC中,BC=,AC=,AB=c.若,如图l,根据勾股定理,则。若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想与c2的关系,并证明你的结论.
三、当堂达标
一、选择题
1.已知|x+y|+(x-2y)2=0,则()
2.一次函数y=kx+b的图象经过点A(0,-2)和B(-3,6)两点,那么该函数的表达式是( )
3.设一个三角形的三边长为3,l-2m,8,则m的取值范围是( )
A.0<m< B. -5<m- 2
C.-2<m <5 D.-<m<-l
4.已知的值为( )
A、 B、- C、 D、-
5.若是完全平方式,则m=( )
A.6 B.4 C.0 D.4或0
6.如果表示a、b为两个实数的点在数轴上的位置如图3-l-8所示,那么化简的结果等于( ),
A.2a B.2b
C.-2a D.-2b
二、填空题
7.已知抛物线的对称轴为直线x=2,且经过点(5,4)和点(1,4)则该抛物线的解析式为____________.
8.用配方法把二次函数 y=x2+3x+l写成 y=(x+m)2+n的形式,则y=__________________-
9.若分式的值为零,则x=________
10函数y=中自变量x的取值范围是_______.
11如果长度分别为5、3、x的三条线段能组成一个三角形,那么x的范围是_______.
12 点(1,6)在双曲线y= 上,则k=______.
三、解答题
13.解下歹方程(组):
14.已知
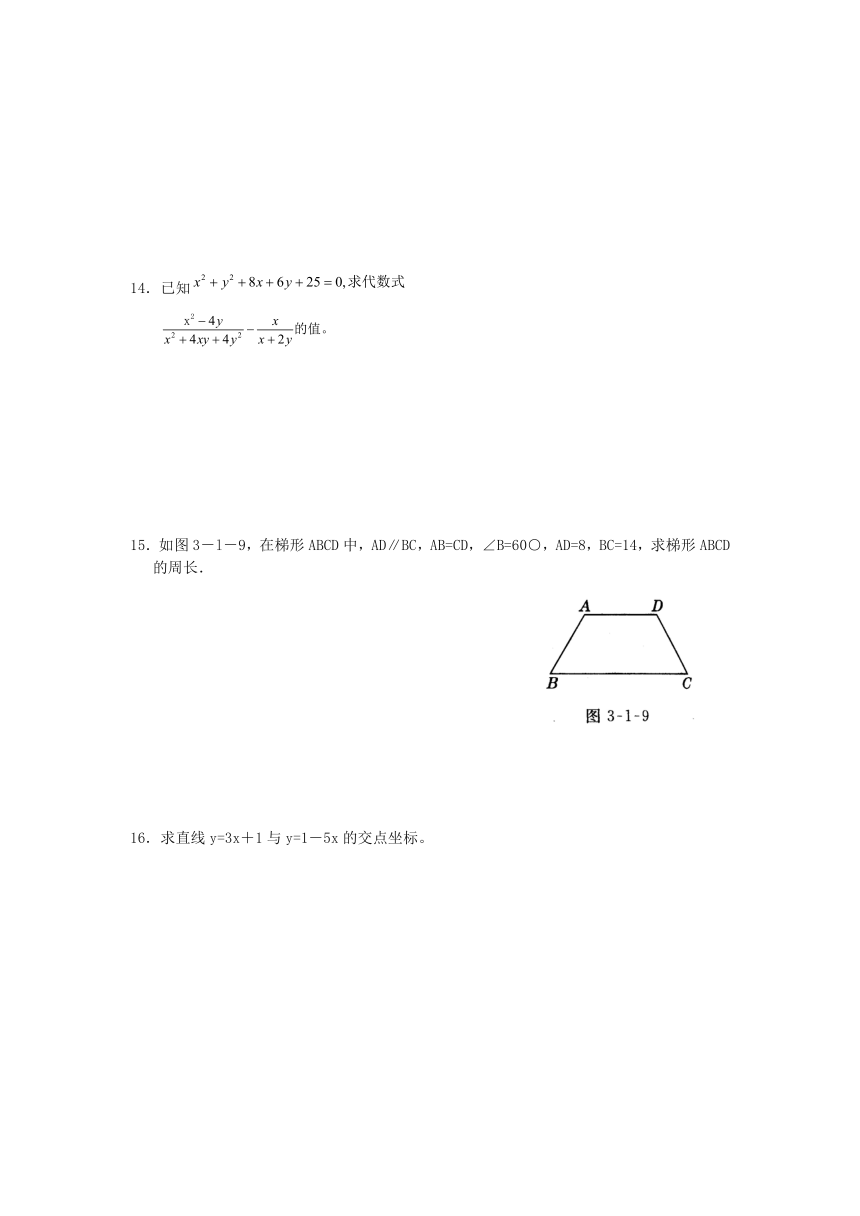
15.如图3-l-9,在梯形ABCD中,AD∥BC,AB=CD,∠B=60○,AD=8,BC=14,求梯形ABCD的周长.
16.求直线y=3x+1与y=1-5x的交点坐标。
参考答案
例题参考答案
【例题1】解:⑴解方程组 得
所以A、B两点的坐标分别为A(-2,4)B(4,-2(2)因为直线y=-x+2与y轴交点D坐标是(0, 2),
所以 所以
点拨:两个函数的图象相交,说明交点处的横坐标和纵坐标,既适合于第一个函数,又适合于第二个函数,所以根据题意可以将函数问题转化为方程组的问题,从而求出交点坐标.
【例题2】解:令y= x—1,则2 y2—5 y +2=0.
所以y1=2或y2=,即x—1=2或x—1=.
所以x=3或x= 故原方程的解为x=3或x=
点拨:很显然,此为解关于x-1的一元二次方程.如果把方程展开化简后再求解会非常麻烦,所以可根据方程的特点,含未·知项的都是含有(x—1)所以可将设为y,这样原方程就可以利用换元法转化为含有y的一元二次方程,问题就简单化了.
【例题3】解:过 D作DE∥AC交BC的延长线于E,则得AD=CE、AC=DE.所以BE=BC+CE=8.
因为 AC⊥BD,所以BD⊥DE.
因为 AB=CD, 所以AC=BD.所以GD=DE.
在Rt△BDE中,BD2+DE2=BE2
所以BD=BE=4,即AC=4.
点拨:此题是根据梯形对角线互相垂直的特点通过平移对角线将等腰梯形转化为直角三角形和平行四边形,使问题得以解决.
【例题4】解:因为,
所以,
即:
所以a=b,a=c, b=c
所以△ABC为等边三角形.
点拨:此题将几何问题转化为代数问题,利用凑完全平方式解决问题.
【例题5】证明:过B作BDAC,交AC的延长线于D。
设CD为,则有
根据勾股定理,得.
即。 ∵,
∴,∴。
点拨:勾股定理是我们非常熟悉的几何知识,对于直角三角形三边具有:的关系,那么锐角三角形、钝角三角形的三边又是怎样的关系呢?我们可以通过作高这条辅助线,将一般三角形转化为直角三角形来确定三边的关系.
当堂达标参考答案
一、总体概述
数学思想是数学内容的进一步提炼和概括,是对数学内容的种本质认识,数学方法是实施有关数学思想的一种方式、途径、手段,数学思想方法是数学发现、发明的关键和动力.抓住数学思想方法,善于迅速调用数学思想方法,更是提高解题能力根本之所在.因此,在复习时要注意体会教材例题、习题以及中考试题中所体现的数学思想和方法,培养用数学思想方法解决问题的意识. 初中数学的主要数学思想是化归思想、分类讨论思想、数形结合思想等.本专题专门复习化归思想.所谓化归思想就是化未知为已知、化繁为简、化难为易.如将分式方程化为整式方程,将代数问题化为几何问题,将四边形问题转化为三角形问题等.实现这种转化的方法有:待定系数法、配方法、整体代人法以及化动为静、由抽象到具体等.
二、典型例题
【例题1】如图3-1-1,反比例函数y=-与一次函数y=-x+2的图象交于A、B两点.
(1)求 A、B两点的坐标;
(2)求△AOB的面积.
【例题2】解方程:
【例题3】如图 3-1-2,梯形 ABCD中,AD∥BC,AB=CD,对角线AC、BD相交于O点,且AC⊥BD,AD=3,BC=5,求AC的长.
【例题4】已知△ABC的三边为a,b,c,且,试判断△ABC的形状.
【例题5】△ABC中,BC=,AC=,AB=c.若,如图l,根据勾股定理,则。若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想与c2的关系,并证明你的结论.
三、当堂达标
一、选择题
1.已知|x+y|+(x-2y)2=0,则()
2.一次函数y=kx+b的图象经过点A(0,-2)和B(-3,6)两点,那么该函数的表达式是( )
3.设一个三角形的三边长为3,l-2m,8,则m的取值范围是( )
A.0<m< B. -5<m- 2
C.-2<m <5 D.-<m<-l
4.已知的值为( )
A、 B、- C、 D、-
5.若是完全平方式,则m=( )
A.6 B.4 C.0 D.4或0
6.如果表示a、b为两个实数的点在数轴上的位置如图3-l-8所示,那么化简的结果等于( ),
A.2a B.2b
C.-2a D.-2b
二、填空题
7.已知抛物线的对称轴为直线x=2,且经过点(5,4)和点(1,4)则该抛物线的解析式为____________.
8.用配方法把二次函数 y=x2+3x+l写成 y=(x+m)2+n的形式,则y=__________________-
9.若分式的值为零,则x=________
10函数y=中自变量x的取值范围是_______.
11如果长度分别为5、3、x的三条线段能组成一个三角形,那么x的范围是_______.
12 点(1,6)在双曲线y= 上,则k=______.
三、解答题
13.解下歹方程(组):
14.已知
15.如图3-l-9,在梯形ABCD中,AD∥BC,AB=CD,∠B=60○,AD=8,BC=14,求梯形ABCD的周长.
16.求直线y=3x+1与y=1-5x的交点坐标。
参考答案
例题参考答案
【例题1】解:⑴解方程组 得
所以A、B两点的坐标分别为A(-2,4)B(4,-2(2)因为直线y=-x+2与y轴交点D坐标是(0, 2),
所以 所以
点拨:两个函数的图象相交,说明交点处的横坐标和纵坐标,既适合于第一个函数,又适合于第二个函数,所以根据题意可以将函数问题转化为方程组的问题,从而求出交点坐标.
【例题2】解:令y= x—1,则2 y2—5 y +2=0.
所以y1=2或y2=,即x—1=2或x—1=.
所以x=3或x= 故原方程的解为x=3或x=
点拨:很显然,此为解关于x-1的一元二次方程.如果把方程展开化简后再求解会非常麻烦,所以可根据方程的特点,含未·知项的都是含有(x—1)所以可将设为y,这样原方程就可以利用换元法转化为含有y的一元二次方程,问题就简单化了.
【例题3】解:过 D作DE∥AC交BC的延长线于E,则得AD=CE、AC=DE.所以BE=BC+CE=8.
因为 AC⊥BD,所以BD⊥DE.
因为 AB=CD, 所以AC=BD.所以GD=DE.
在Rt△BDE中,BD2+DE2=BE2
所以BD=BE=4,即AC=4.
点拨:此题是根据梯形对角线互相垂直的特点通过平移对角线将等腰梯形转化为直角三角形和平行四边形,使问题得以解决.
【例题4】解:因为,
所以,
即:
所以a=b,a=c, b=c
所以△ABC为等边三角形.
点拨:此题将几何问题转化为代数问题,利用凑完全平方式解决问题.
【例题5】证明:过B作BDAC,交AC的延长线于D。
设CD为,则有
根据勾股定理,得.
即。 ∵,
∴,∴。
点拨:勾股定理是我们非常熟悉的几何知识,对于直角三角形三边具有:的关系,那么锐角三角形、钝角三角形的三边又是怎样的关系呢?我们可以通过作高这条辅助线,将一般三角形转化为直角三角形来确定三边的关系.
当堂达标参考答案
同课章节目录
