连云港市灌南县灌河中学2012届中考数学二轮专题复习四 实际应用题
文档属性
| 名称 | 连云港市灌南县灌河中学2012届中考数学二轮专题复习四 实际应用题 |

|
|
| 格式 | zip | ||
| 文件大小 | 305.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-20 00:00:00 | ||
图片预览



文档简介
中考数学专题复习四 实际应用题
一、总体概述
近年各地中考中总有联系社会热点及现实生产生活的应用题,以考察学生用数学知识解决实际问题的能力。这类问题往往具有较强的现实意义和时代感,其背景贴近生活,贴近实际,有利于促进学生数学应用意识的培养和提高。
二、典型例题
例1 利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的二次函数关系式(不要求写出x的取值范围);
(3)请把(2)中的二次函数配方成的形式,并据此说明,该经销店要
获得最大月利润,售价应定为每吨多少元;
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
[解析] (1)=60(吨).
(2),
化简得: .
(3).
利达经销店要获得最大月利润,材料的售价应定为每吨210元.
(4)我认为,小静说的不对.
理由:方法一:当月利润最大时,x为210元,
而对于月销售额来说,
当x为160元时,月销售额W最大.
∴当x为210元时,月销售额W不是最大.
∴小静说的不对.
方法二:当月利润最大时,x为210元,此时,月销售额为17325元;
而当x为200元时,月销售额为18000元.∵17325<18000,
∴当月利润最大时,月销售额W不是最大.
∴小静说的不对.
例2 西南五省干旱牵动着全国亿万人民的心,某校为 灾区开展了“献出我们的爱” 赈灾捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动,下表是小明对全班捐款情况的统计表:
捐款(元) 10 15 30 50 60
人数 3 6 11 13 6
因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数、中位数分别是多少?
[解析](1) 被污染处的人数为11人
设被污染处的捐款数为元,则
11+1460=50×38
解得 =40
答:(1)被污染处的人数为11人,被污染处的捐款数为40元.
(2)捐款金额的中位数是40元,捐款金额的众数是50元
[解题启示]
这类题目的特点是由图象或表格提供一组数据,要求从图表中获取有效信息并加以处理,因而寻找数据间的相等关系是解答这类问题的突破口
例3 有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.图是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
(1)乙队开挖到30米时,用了_____小时.开挖6小时时, 甲队比乙队多挖了______米;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
③开挖几小时后,甲队所挖掘河渠的长度开始超过乙队?
(3)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.问甲队从开挖到完工所挖河渠的长度为多少米?
[解析] (1)2;10;
(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式为y=k1x,
由图可知,函数图象过点(6,60),
∴6 k1=60,解得k1=10,
∴y =10x.
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y =k2x+b,
由图可知,函数图象过点(2,30)、(6,50),
∴ 解得
∴y =5x+20.
③由题意,得10x>5x+20,解得x>4.
所以,4小时后,甲队挖掘河渠的长度开始超过乙队.
(3)由图可知,甲队速度是:60÷6=10(米/时).
设甲队从开挖到完工所挖河渠的长度为z米,依题意,得
解得 =110.
答:甲队从开挖到完工所挖河渠的长度为110米.
[解题启示]
解决这类题目主要是通过观察图象获取信息并用方程的思想来解决问题
例4 在购买“上海世博“门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
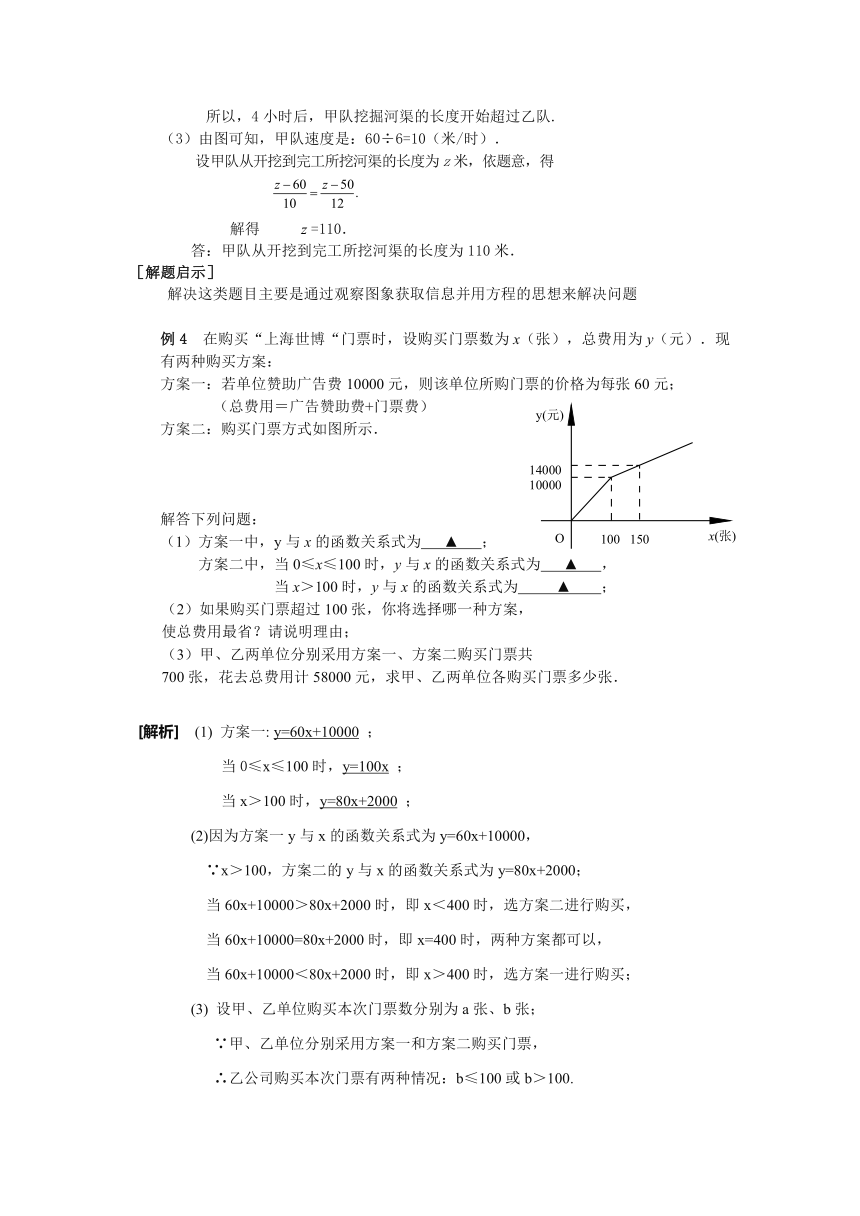
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为 ▲ ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ▲ ,
当x>100时,y与x的函数关系式为 ▲ ;
(2)如果购买门票超过100张,你将选择哪一种方案,
使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买门票共
700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
[解析] (1) 方案一: y=60x+10000 ;
当0≤x≤100时,y=100x ;
当x>100时,y=80x+2000 ;
(2)因为方案一y与x的函数关系式为y=60x+10000,
∵x>100,方案二的y与x的函数关系式为y=80x+2000;
当60x+10000>80x+2000时,即x<400时,选方案二进行购买,
当60x+10000=80x+2000时,即x=400时,两种方案都可以,
当60x+10000<80x+2000时,即x>400时,选方案一进行购买;
(3) 设甲、乙单位购买本次门票数分别为a张、b张;
∵甲、乙单位分别采用方案一和方案二购买门票,
∴乙公司购买本次门票有两种情况:b≤100或b>100.
当b≤100时,乙公司购买本次门票费为100b,
解得不符合题意,舍去;
当b>100时,乙公司购买本次门票费为80b+2000,
解得 符合题意
答:甲、乙单位购买本次门票分别为500张、200张.
[解题启示]
方案一中可直接求出函数关系式,方案二中结合图象利用待定系数法可以求出函数关系式。(2)选择哪一种方案,使总费用最省,就把这两种方案进行分类比较。
(3)中要就不同的情况分类求解。
三、当堂达标
1.甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球
从起跑线起跑,绕过P点跑回到起跑线(如图所示);途中乒乓
球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲
同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,
甲同学说:“我俩所用的全部时间的和为50秒”,乙同学说:“捡球
过程不算在内时,甲的速度是我的1.2倍”.根据图文信息,请问哪
位同学获胜?
2. 如图某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即)为1︰1.2,坝高为5米,现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4,已知堤坝总长度为4000米.
(1)求完成该工程需要多少土方
(2)该工程由甲、乙两个工程队同时合作完成.按原计划需要20天.准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率,甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成.问这两个工程队原计划每天各完成多少土方?
3. 某农户种植一种经济作物,总用水量(米)与种植时间(天)之间的函数关系式如图10所示.
(1)第天的总用水量为多少米?
(2)当时,求与之间的函数关系式.
(3)种植时间为多少天时,总用水量达到7000米?
4.某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 管理人员 普通工作人员
人员结构 总经理 部门经理 科研人员 销售人员 高级技工 中级技工 勤杂工
员工数(名) 1 3 2 3 24 1
每人月工资(元) 21000 8400 2025 2200 1800 1600 950
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数为2500元,
中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作
人员.请你回答右图中小张的
问题,并指出用(2)中的哪个
数据向小张介绍员工的月工资
实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资(结果保留整数),并判断能否反映该公司员工的月工资实际水平.
5.某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为,BC所在抛物线的解析式为,且已知.
(1)设是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一直铺到山脚,为什么?
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为.试求索道的最大悬空高度.
中考数学专题复习 实际应用题
参考答案
1.解一:设乙同学的速度为米/秒,则甲同学的速度为米/秒, 根据题意,得, 解得 经检验,是方程的解,且符合题意.
甲同学所用的时间为:(秒), 乙同学所用的时间为:(秒).
,乙同学获胜.
解二:设甲同学所用的时间为秒,乙同学所用的时间为秒, 根据题意,得 解得 经检验,,是方程组的解,且符合题意.
,乙同学获胜
2(1)作DG⊥AB于G,作EH⊥AB于H. ∵CD∥AB,∴EH=DG
∵,∴AG=6米,∵,∴FH=7米, ∴FA=FH+GH-AG=7+1-6=2(米)
∴SADEF=(ED+AF)·EH=(1+2)×5=7.5(平方米)V=7.5×4000=30000 (立方米)
(2)设甲队原计划每天完成x立方米土方,乙队原计划每天完成y立方米土方.
根据题意,得 化简,得
解之,得 HYPERLINK "http://" 答:甲队原计划每天完成1000立方米土方,乙队原计划每天完成500立方米土方.
3. 解:(1)第天的总用水量为米 (2)当时,设
∵函数图象经过点(20,1000),(30,4000)∴ 解得
∴与之间的函数关系式为:y=3005000
(3)当y =7000时 有7000=3005000 解得=40答 :种植时间为40天时,总用水量达到7000米
4.(1)由表中数据知有16名; (2)由表中数据知中位数为1700;众数为1600; (3)这个经理的介绍不能反映该公司员工的月工资实际水平. 用1700元或1600元来介绍更合理些.(说明:该问中只要写对其中一个数据或相应统计量(中位数或众数)也可以)
(4)≈1713(元) 能反映.
5.(1)∵是山坡线AB上任意一点,∴,, ∴, ∵,∴=4,∴
(2)在山坡线AB上,,
①令,得 ;令,得
∴第一级台阶的长度为(百米)(厘米)
同理,令、,可得、
∴第二级台阶的长度为(百米)(厘米)
第三级台阶的长度为(百米)(厘米)
②取点,又取,则
∵
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性)
②另解:连接任意一段台阶的两端点P、Q,如图
∵这种台阶的长度不小于它的高度
∴
当其中有一级台阶的长大于它的高时,
在题设图中,作于H
则,又第一级台阶的长大于它的高
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
(3)
、、、
由图可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值
索道在BC上方时,悬空高度
当时,
∴索道的最大悬空高度为米.
6
2
O
x(时)
y(米)
30
60
乙
甲
50
10000
14000
100
150
O
x(张)
y(元)
P
30米
l
O
(天)
y(米)
4000
1000
30
20
部门经理
小张
这个经理的介绍能反映该公司员工的月工资实际水平吗?
欢迎你来我们公司应聘!我公司员工的月平均工资是2500元,薪水是较高的.
上山方向
长度
高度
上山方向
一、总体概述
近年各地中考中总有联系社会热点及现实生产生活的应用题,以考察学生用数学知识解决实际问题的能力。这类问题往往具有较强的现实意义和时代感,其背景贴近生活,贴近实际,有利于促进学生数学应用意识的培养和提高。
二、典型例题
例1 利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的二次函数关系式(不要求写出x的取值范围);
(3)请把(2)中的二次函数配方成的形式,并据此说明,该经销店要
获得最大月利润,售价应定为每吨多少元;
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
[解析] (1)=60(吨).
(2),
化简得: .
(3).
利达经销店要获得最大月利润,材料的售价应定为每吨210元.
(4)我认为,小静说的不对.
理由:方法一:当月利润最大时,x为210元,
而对于月销售额来说,
当x为160元时,月销售额W最大.
∴当x为210元时,月销售额W不是最大.
∴小静说的不对.
方法二:当月利润最大时,x为210元,此时,月销售额为17325元;
而当x为200元时,月销售额为18000元.∵17325<18000,
∴当月利润最大时,月销售额W不是最大.
∴小静说的不对.
例2 西南五省干旱牵动着全国亿万人民的心,某校为 灾区开展了“献出我们的爱” 赈灾捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动,下表是小明对全班捐款情况的统计表:
捐款(元) 10 15 30 50 60
人数 3 6 11 13 6
因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数、中位数分别是多少?
[解析](1) 被污染处的人数为11人
设被污染处的捐款数为元,则
11+1460=50×38
解得 =40
答:(1)被污染处的人数为11人,被污染处的捐款数为40元.
(2)捐款金额的中位数是40元,捐款金额的众数是50元
[解题启示]
这类题目的特点是由图象或表格提供一组数据,要求从图表中获取有效信息并加以处理,因而寻找数据间的相等关系是解答这类问题的突破口
例3 有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.图是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
(1)乙队开挖到30米时,用了_____小时.开挖6小时时, 甲队比乙队多挖了______米;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
③开挖几小时后,甲队所挖掘河渠的长度开始超过乙队?
(3)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.问甲队从开挖到完工所挖河渠的长度为多少米?
[解析] (1)2;10;
(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式为y=k1x,
由图可知,函数图象过点(6,60),
∴6 k1=60,解得k1=10,
∴y =10x.
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y =k2x+b,
由图可知,函数图象过点(2,30)、(6,50),
∴ 解得
∴y =5x+20.
③由题意,得10x>5x+20,解得x>4.
所以,4小时后,甲队挖掘河渠的长度开始超过乙队.
(3)由图可知,甲队速度是:60÷6=10(米/时).
设甲队从开挖到完工所挖河渠的长度为z米,依题意,得
解得 =110.
答:甲队从开挖到完工所挖河渠的长度为110米.
[解题启示]
解决这类题目主要是通过观察图象获取信息并用方程的思想来解决问题
例4 在购买“上海世博“门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为 ▲ ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ▲ ,
当x>100时,y与x的函数关系式为 ▲ ;
(2)如果购买门票超过100张,你将选择哪一种方案,
使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买门票共
700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
[解析] (1) 方案一: y=60x+10000 ;
当0≤x≤100时,y=100x ;
当x>100时,y=80x+2000 ;
(2)因为方案一y与x的函数关系式为y=60x+10000,
∵x>100,方案二的y与x的函数关系式为y=80x+2000;
当60x+10000>80x+2000时,即x<400时,选方案二进行购买,
当60x+10000=80x+2000时,即x=400时,两种方案都可以,
当60x+10000<80x+2000时,即x>400时,选方案一进行购买;
(3) 设甲、乙单位购买本次门票数分别为a张、b张;
∵甲、乙单位分别采用方案一和方案二购买门票,
∴乙公司购买本次门票有两种情况:b≤100或b>100.
当b≤100时,乙公司购买本次门票费为100b,
解得不符合题意,舍去;
当b>100时,乙公司购买本次门票费为80b+2000,
解得 符合题意
答:甲、乙单位购买本次门票分别为500张、200张.
[解题启示]
方案一中可直接求出函数关系式,方案二中结合图象利用待定系数法可以求出函数关系式。(2)选择哪一种方案,使总费用最省,就把这两种方案进行分类比较。
(3)中要就不同的情况分类求解。
三、当堂达标
1.甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球
从起跑线起跑,绕过P点跑回到起跑线(如图所示);途中乒乓
球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲
同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,
甲同学说:“我俩所用的全部时间的和为50秒”,乙同学说:“捡球
过程不算在内时,甲的速度是我的1.2倍”.根据图文信息,请问哪
位同学获胜?
2. 如图某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即)为1︰1.2,坝高为5米,现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4,已知堤坝总长度为4000米.
(1)求完成该工程需要多少土方
(2)该工程由甲、乙两个工程队同时合作完成.按原计划需要20天.准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率,甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成.问这两个工程队原计划每天各完成多少土方?
3. 某农户种植一种经济作物,总用水量(米)与种植时间(天)之间的函数关系式如图10所示.
(1)第天的总用水量为多少米?
(2)当时,求与之间的函数关系式.
(3)种植时间为多少天时,总用水量达到7000米?
4.某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 管理人员 普通工作人员
人员结构 总经理 部门经理 科研人员 销售人员 高级技工 中级技工 勤杂工
员工数(名) 1 3 2 3 24 1
每人月工资(元) 21000 8400 2025 2200 1800 1600 950
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数为2500元,
中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作
人员.请你回答右图中小张的
问题,并指出用(2)中的哪个
数据向小张介绍员工的月工资
实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资(结果保留整数),并判断能否反映该公司员工的月工资实际水平.
5.某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为,BC所在抛物线的解析式为,且已知.
(1)设是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一直铺到山脚,为什么?
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为.试求索道的最大悬空高度.
中考数学专题复习 实际应用题
参考答案
1.解一:设乙同学的速度为米/秒,则甲同学的速度为米/秒, 根据题意,得, 解得 经检验,是方程的解,且符合题意.
甲同学所用的时间为:(秒), 乙同学所用的时间为:(秒).
,乙同学获胜.
解二:设甲同学所用的时间为秒,乙同学所用的时间为秒, 根据题意,得 解得 经检验,,是方程组的解,且符合题意.
,乙同学获胜
2(1)作DG⊥AB于G,作EH⊥AB于H. ∵CD∥AB,∴EH=DG
∵,∴AG=6米,∵,∴FH=7米, ∴FA=FH+GH-AG=7+1-6=2(米)
∴SADEF=(ED+AF)·EH=(1+2)×5=7.5(平方米)V=7.5×4000=30000 (立方米)
(2)设甲队原计划每天完成x立方米土方,乙队原计划每天完成y立方米土方.
根据题意,得 化简,得
解之,得 HYPERLINK "http://" 答:甲队原计划每天完成1000立方米土方,乙队原计划每天完成500立方米土方.
3. 解:(1)第天的总用水量为米 (2)当时,设
∵函数图象经过点(20,1000),(30,4000)∴ 解得
∴与之间的函数关系式为:y=3005000
(3)当y =7000时 有7000=3005000 解得=40答 :种植时间为40天时,总用水量达到7000米
4.(1)由表中数据知有16名; (2)由表中数据知中位数为1700;众数为1600; (3)这个经理的介绍不能反映该公司员工的月工资实际水平. 用1700元或1600元来介绍更合理些.(说明:该问中只要写对其中一个数据或相应统计量(中位数或众数)也可以)
(4)≈1713(元) 能反映.
5.(1)∵是山坡线AB上任意一点,∴,, ∴, ∵,∴=4,∴
(2)在山坡线AB上,,
①令,得 ;令,得
∴第一级台阶的长度为(百米)(厘米)
同理,令、,可得、
∴第二级台阶的长度为(百米)(厘米)
第三级台阶的长度为(百米)(厘米)
②取点,又取,则
∵
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性)
②另解:连接任意一段台阶的两端点P、Q,如图
∵这种台阶的长度不小于它的高度
∴
当其中有一级台阶的长大于它的高时,
在题设图中,作于H
则,又第一级台阶的长大于它的高
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
(3)
、、、
由图可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值
索道在BC上方时,悬空高度
当时,
∴索道的最大悬空高度为米.
6
2
O
x(时)
y(米)
30
60
乙
甲
50
10000
14000
100
150
O
x(张)
y(元)
P
30米
l
O
(天)
y(米)
4000
1000
30
20
部门经理
小张
这个经理的介绍能反映该公司员工的月工资实际水平吗?
欢迎你来我们公司应聘!我公司员工的月平均工资是2500元,薪水是较高的.
上山方向
长度
高度
上山方向
同课章节目录
