第18章 平行四边形 单元测试(原版+解析版)
文档属性
| 名称 | 第18章 平行四边形 单元测试(原版+解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 14:06:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教版八年级下册数学
单元测评培优卷(原版+解析版)
第18章
平行四边形
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·成都市初三期末)下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
2.(2021·广东八年级期末)如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
3.(2020·温州外国语学校八年级月考)从①;②;③;④.这四个条件中选取两个,使四边形成为平行四边形.下面不能说明是平行四边形的是(
)
A.①②
B.①③
C.②④
D.①④
4.(2021·陕西九年级期末)如图,矩形的对角线,相交于点,,若的周长比的周长大10,则的长为(
).
A.
B.
C.10
D.20
5.(2020·江西新余初三期末)如图,在任意四边形中,,,,分别是,,,上的点,对于四边形的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是(
)
A.当,,,是各边中点,且时,四边形为菱形
B.当,,,是各边中点,且时,四边形为矩形
C.当,,,不是各边中点时,四边形可以为平行四边形
D.当,,,不是各边中点时,四边形不可能为菱形
6.(2020·湖北九年级期末)如图,在中,,,,依据尺规作图的痕迹,则的面积为(
)
A.12
B.
C.
D.
7.(2020·无锡市前洲中学初三月考)如图,在菱形中对角线相交于点,直线交
于点,则的长(
)
A.4
B.4.
8
C.2.
4
D.3.
2
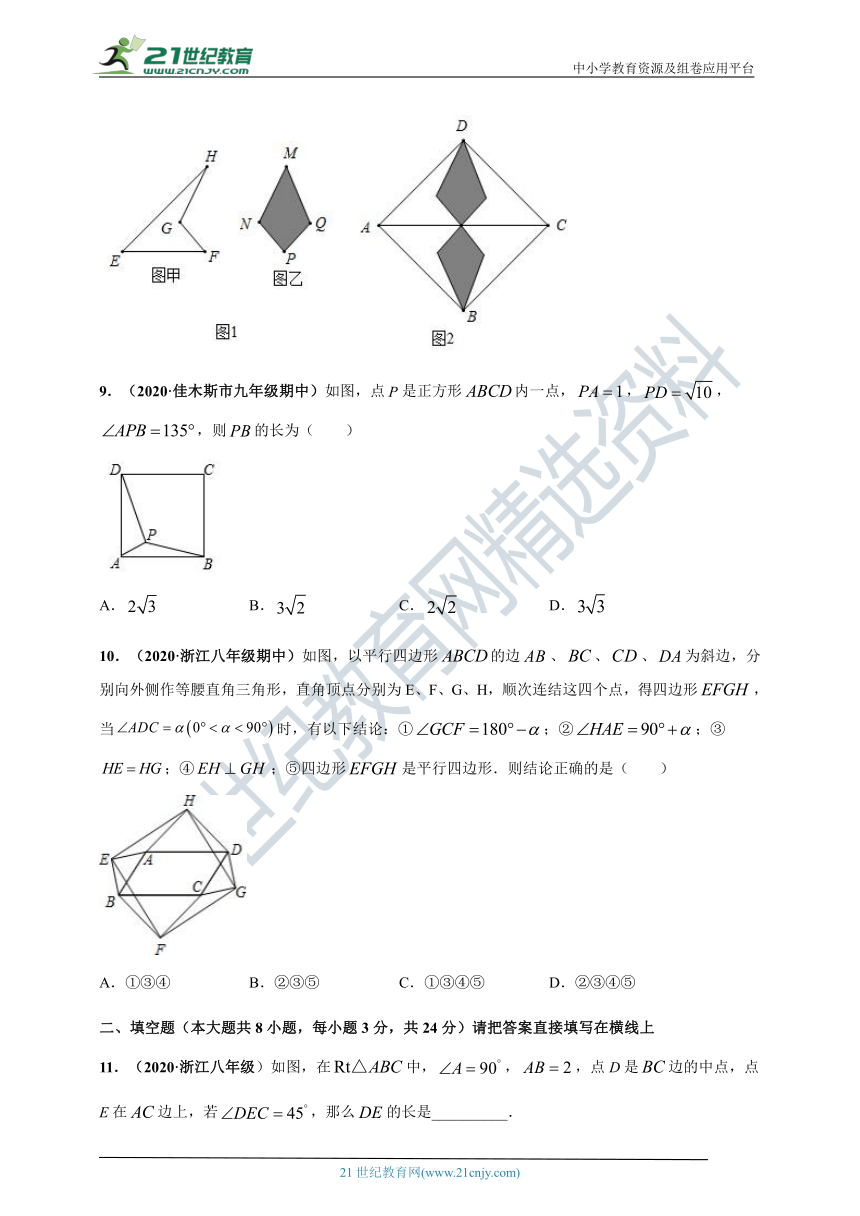
8.(2021·浙江八年级期末)图1中甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD.已知图甲中,,,图乙中
,则图2中正方形的对角线AC长为( )
A.
B.
C.
D.
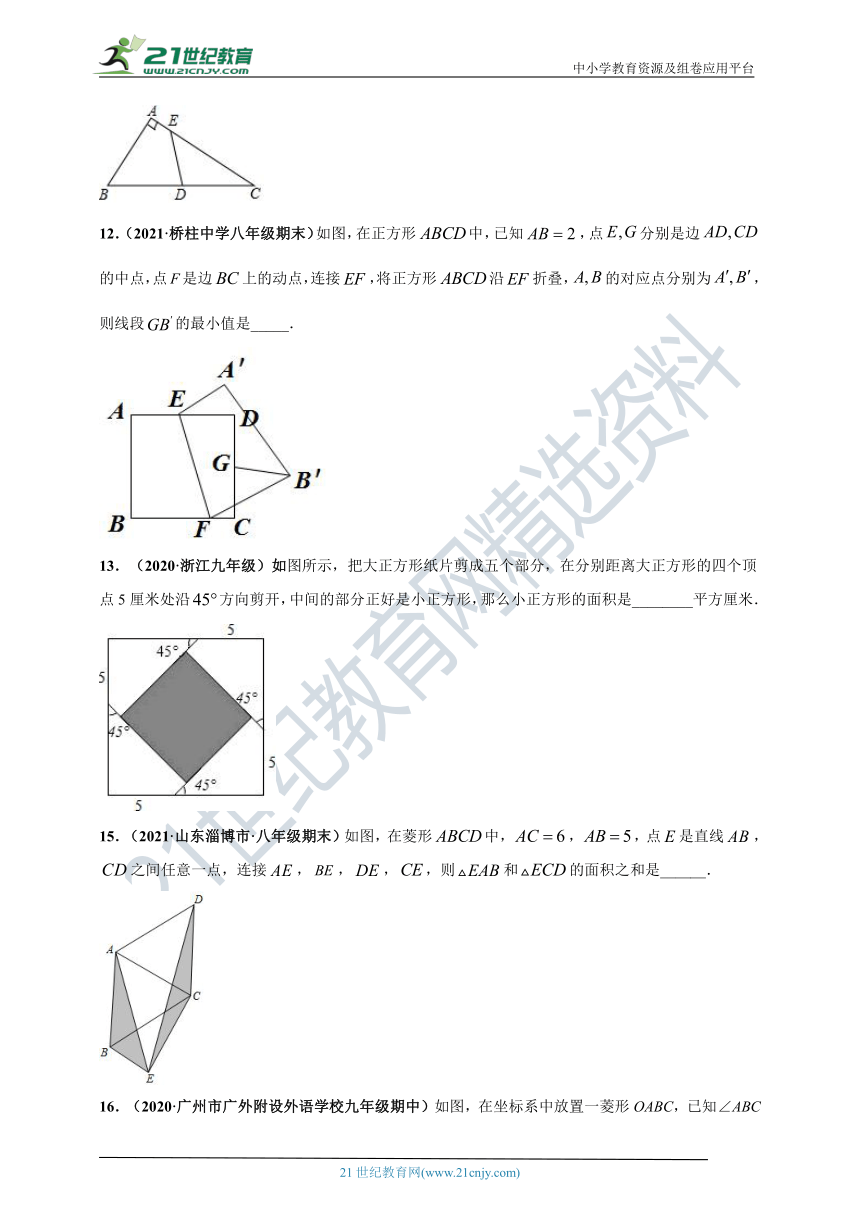
9.(2020·佳木斯市九年级期中)如图,点是正方形内一点,,,,则的长为(
)
A.
B.
C.
D.
10.(2020·浙江八年级期中)如图,以平行四边形的边、、、为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形,当时,有以下结论:①;②;③;④;⑤四边形是平行四边形.则结论正确的是(
)
A.①③④
B.②③⑤
C.①③④⑤
D.②③④⑤
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·浙江八年级)如图,在中,,,点D是边的中点,点E在边上,若,那么的长是__________.
12.(2021·桥柱中学八年级期末)如图,在正方形中,已知,点分别是边的中点,点F是边上的动点,连接,将正方形沿折叠,的对应点分别为,则线段的最小值是_____.
13.(2020·浙江九年级)如图所示,把大正方形纸片剪成五个部分,在分别距离大正方形的四个顶点5厘米处沿方向剪开,中间的部分正好是小正方形,那么小正方形的面积是________平方厘米.
15.(2021·山东淄博市·八年级期末)如图,在菱形中,,,点是直线,之间任意一点,连接,,,,则和的面积之和是______.
16.(2020·广州市广外附设外语学校九年级期中)如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2019次,点B的落点依次为B1,B2,B3,…,则B2019的坐标为_____.
17.(2021·黑龙江九年级期末)如图,在矩形中,,为中点,点为上一动点,将沿所在直线折叠到的位置,连接,则的最小值为__________.
18.(2020·浙江九年级期末)如图,在平行四边形中,,F是的中点,,垂足E在线段上.下列结论①;②;③;④中,一定成立的是_________.(请填序号)
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·广东龙岭初级中学八年级月考)如图,在矩形ABCD中,AB=6,BC=10,点E在边CD上,连接AE,将四边形ABCE沿直线AE折叠,得到多边形,且恰好经过点D.
(1)线段DC′的长度;(2)求ADE的面积.
20.(2021·贵州九年级期末)如图,已知四边形是平行四边形,E是延长线上一点且,连接,.(1)求证:四边形是平行四边形,(2)连接,若,,求的面积.
21.(2020·浙江八年级期末)如图,在四边形中,,,,,,动点N从点D出发,以每秒的速度在射线上运动到C点返回,动点M从点A出发,在线段上,以每秒的速度向点B运动,点M,N分别从点A,D同时出发.当点M运动到点B时,点N随之停止运动,设运动时间为t(秒).(1)当t为何值时,四边形是平行四边形.(2)是否存在点N,使是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
22.(2020·浙江丽水初三期末)如图,在菱形中,是边上的动点,作交于点,在上取点使,连结(1)求的度数;(2)求证:(3)若是的中点,当为何值时,是等腰三角形.
23.(2020·辽宁九年级期中)如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
24.(2020·浙江八年级月考)定义,我们把对角线互相垂直的四边形叫做和美四边形,对角线交点作为和美四边形的中心.
(1)写出一种你学过的和美四边形______;
(2)顺次连接和美四边形四边中点所得四边形是(
)
A.矩形
B,菱形
C.正方形
D.无法确定
(3)如图1,点O是和美四边形的中心,分别是边的中点,连接,记四边形的面积为,用等式表示的数量关系(无需说明理由)
(4)如图2,四边形是和美四边形,若,求的长.
25.(2020·吉林省初三一模)(教材呈现)如图是八年级下册数学教材第117页的部分内容.
结合图①,补全证明过程.
(应用)如图②,直线EF分别交矩形ABCD的边AD、BC于点E、F,将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=3,BC=4,则四边形ABFE的周长为
.
(拓展)如图③,直线EF分别交?ABCD的边AD、BC于点E、F,将?ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=,BC=4,∠C=45°,则EF的长为
.
2020-2021学年人教版八年级下册数学
单元测评培优卷(原版+解析版)
第18章
平行四边形
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·成都市初三期末)下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
【答案】D
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解析】A、一组对边平行,另一组对边相等的四边形有可能是等腰梯形,故A选项错误;
B、对角线互相垂直的四边形也可能是一般四边形,故B选项错误;
C、对角线相等的四边形有可能是等腰梯形,故C选项错误.
D、一组邻边相等的矩形是正方形,故D选项正确.故选D.
【点睛】本题考查特殊平行四边形的判定,需熟练掌握各特殊四边形的特点.
2.(2021·广东八年级期末)如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
【答案】B
【分析】根据三角形中位线定理解答即可.
【详解】解:∵点D和点E分别是BC和BA的中点,
∴DE是△ABC的中位线,∴DE=AC=4=2,故选:B.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
3.(2020·温州外国语学校八年级月考)从①;②;③;④.这四个条件中选取两个,使四边形成为平行四边形.下面不能说明是平行四边形的是(
)
A.①②
B.①③
C.②④
D.①④
【答案】D
【分析】根据平行四边形的判定方法逐项判断即可.
【详解】解:A、选①②,即四边形ABCD满足,,根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD是平行四边形,故本选项不符合题意;
B、选①③,即四边形ABCD满足,,根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD是平行四边形,故本选项不符合题意;
C、选②④,即四边形ABCD满足,,根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD是平行四边形,故本选项不符合题意;
D、选①④,即四边形ABCD满足,,一组对边平行,另一组对边相等,不能判定四边形ABCD是平行四边形,故本选项符合题意.故选:D.
【点睛】本题考查了平行四边形的判定,属于基础题型,熟知平行四边形的判定方法是正确判断的关键.
4.(2021·陕西九年级期末)如图,矩形的对角线,相交于点,,若的周长比的周长大10,则的长为(
).
A.
B.
C.10
D.20
【答案】A
【分析】由矩形的性质和已知条件求出AB=BC,BC=10,即可得出答案.
【详解】解:∵四边形ABCD是矩形,∴AO=CO=DO=BO,AD=BC,∠ABC=90°,AB∥CD,
∴∠BAC=∠ACD=30°,∴AB=BC,
∵△ABC的周长=AB+AC+BC=AB+AO+OC+BC,△AOB的周长=AB+AO+BO,
又∵ABC的周长比△AOB的周长长10,
∴AB+AC+BC-(AB+AO+BO)=BC=10,∴AB=BC=;故选:A.
【点睛】本题考查了矩形的性质、含30°角的直角三角形的性质等知识,熟练掌握矩形的性质,求出BC的长是解题的关键.
5.(2020·江西新余初三期末)如图,在任意四边形中,,,,分别是,,,上的点,对于四边形的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是(
)
A.当,,,是各边中点,且时,四边形为菱形
B.当,,,是各边中点,且时,四边形为矩形
C.当,,,不是各边中点时,四边形可以为平行四边形
D.当,,,不是各边中点时,四边形不可能为菱形
【答案】D
【分析】当E,F,G,H是四边形ABCD各边中点时,连接AC、BD,如图,根据三角形的中位线定理可得四边形EFGH是平行四边形,然后根据菱形的定义和矩形的定义即可对A、B两项进行判断;画出符合题意的平行四边形,但满足,,,不是各边中点即可判断C项;画出符合题意的菱形,但满足,,,不是各边中点即可判断D项,进而可得答案.
【解析】A.当E,F,G,H是四边形ABCD各边中点时,连接AC、BD,如图,则由三角形的中位线定理得:EH=BD,EH∥BD;FG=BD,FG∥BD,所以EH=FG,EH∥FG,即四边形EFGH是平行四边形;
当AC=BD时,∵EH=BD,EF=AC,∴EF=EH,故四边形EFGH为菱形,故A正确;
B.当E,F,G,H是四边形ABCD各边中点,且AC⊥BD时,如上图,由三角形的中位线定理可得:EH∥BD,EF∥AC,所以EH⊥EF,故平行四边形EFGH为矩形,故B正确;
C.如图所示,若EF∥HG,EF=HG,则四边形EFGH为平行四边形,此时E,F,G,H不是四边形ABCD各边中点,故C正确;
D.如图所示,若EF=FG=GH=HE,则四边形EFGH为菱形,此时E,F,G,H不是四边形ABCD各边中点,故D错误;故选:D.
【点睛】本题考查了中点四边形以及特殊四边形的判定等知识,熟练掌握中点四边形的形状、会画出符合题意的反例图形是解题关键.
6.(2020·湖北九年级期末)如图,在中,,,,依据尺规作图的痕迹,则的面积为(
)
A.12
B.
C.
D.
【答案】C
【分析】由作图痕迹可得EF为AB的中垂线,结合判断出△ABE为等边三角形,从而结合边长求出在BC边上的高为,再根据比例关系求得BC的长度,最终计算面积即可.
【详解】设尺规作图所得直线与AB交于F点,根据题意可得EF为AB的中垂线,∴AE=BE,
又∵,∴△ABE为等边三角形,边长AB=CD=4,∴BF=2,BE=4,,∴在BC边上的高为,
又∵,BE=4,∴EC=2,BC=2+4=6,
∴=×6=,故选:C.
【点睛】本题考查平行四边形的性质,中垂线的识别与性质,以及等边三角形的判定与性质,准确根据作图痕迹总结出等边三角形是解题关键.
7.(2020·无锡市前洲中学初三月考)如图,在菱形中对角线相交于点,直线交
于点,则的长(
)
A.4
B.4.
8
C.2.
4
D.3.
2
【答案】D
【分析】根据菱形的性质可得AC⊥DB,AO=,BO=,然后利用勾股定理计算出AB长,再根据菱形的面积公式得到S菱形ABCD=,进而得到△AOB的面积,然后根据直角三角形的面积计算出EO长,再利用勾股定理求出AE即可.
【解析】解:∵四边形ABCD是菱形,
∴AC⊥DB,AO=,BO=
∵AC=8,BD=6,∴AO=4,BO=3,S菱形ABCD=
∴AB=,S△AOB=6,即∴EO=,
在Rt△AOE中,,故选:D.
【点睛】此题主要考查了菱形的性质、面积、以及勾股定理,关键是掌握菱形的两条对角线互相垂直.
8.(2021·浙江八年级期末)图1中甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD.已知图甲中,,,图乙中
,则图2中正方形的对角线AC长为( )
A.
B.
C.
D.
【答案】D
【分析】连接,过点作交于点,根据甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD,可得是等腰直角三角形,则可求得,,根据勾股定理,可得:,,则有,,根据正方形的对角线可求出答案.
【详解】解:如图示,连接,过点作交于点,
∵甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD.
∴根据题意,根据对称性可得是等腰直角三角形,则有:,
∵,,∴,,
又∵,,∴根据勾股定理,可得:,,
则有,∴,
∴正方形的对角线,故选:D.
【点睛】本题考查了正方形的性质,勾股定理,直角三角形的性质,熟悉相关性质是解题的关键.
9.(2020·佳木斯市九年级期中)如图,点是正方形内一点,,,,则的长为(
)
A.
B.
C.
D.
【答案】C
【分析】将绕着点A顺时针旋转90°得到,连接,则是等腰直角三角形,,然后根据勾股定理即可得到结论.
【详解】将绕着点A顺时针旋转90°得到,连接,则是等腰直角三角形
∴∴,∴
∵∴∴故选C.
【点睛】本题考查了正方形的性质,旋转的性质,等腰直角三角形的判定和性质,和勾股定理,正确的作出辅助线是本题的关键.
10.(2020·浙江八年级期中)如图,以平行四边形的边、、、为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形,当时,有以下结论:①;②;③;④;⑤四边形是平行四边形.则结论正确的是(
)
A.①③④
B.②③⑤
C.①③④⑤
D.②③④⑤
【答案】D
【分析】根据平行四边形性质得出∠ABC=∠ADC=α,∠BAD=∠BCD,AB=CD,AD=BC,AD∥BC,AB∥CD,根据等腰直角三角形得出BE=AE=CG=DG,AH=DH=BF=CF,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠EDA=45°,求出∠HAE=∠HDG=∠FCG=∠FBE=90°+α,证△FBE≌△HAE≌△HDG≌△FCG,推出∠BFE=∠GFC,EF=EH=HG=GF,求出∠EFG=90°,根据正方形性质得出即可.
【详解】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=α,∠BAD=∠BCD,AB=CD,AD=BC,AD∥BC,AB∥CD,
∵平行四边形ABCD的边AB、BC、CD、DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,∴BE=AE=CG=DG,AH=DH=BF=CF,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠EDA=45°,∵AB∥CD,∴∠BAD=∠BCD=180°-α,
∴∠EAH=360°-45°-45°-(180°-α)=90°+α,∠GCF=360°-45°-45°-(180°-α)=90°+α,
∴①错误;②正确;∠HDG=45°+45°+α=90°+α,∠FBE=45°+45°+α=90°+α,
∴∠HAE=∠HDG=∠FCG=∠FBE,在△FBE、△HAE、△HDG、△FCG中,
,∴△FBE≌△HAE≌△HDG≌△FCG(SAS),
∴∠BFE=∠GFC,EF=EH=HG=GF,③正确;∴四边形EFGH是菱形,
∵∠BFC=90°=∠BFE+∠EFC=∠GFC+∠CFE,∴∠EFG=90°,
∴四边形EFGH是正方形,⑤正确;∴EH⊥GH,④正确;故选:D.
【点睛】本题考查了等腰直角三角形,全等三角形的性质和判定,正方形的判定,平行四边形的性质,菱形的判定的应用,主要考查学生的推理能力.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·浙江八年级)如图,在中,,,点D是边的中点,点E在边上,若,那么的长是__________.
【答案】
【分析】过D作DF⊥AC于F,得到AB∥DF,求得AF=CF,根据三角形中位线定理得到DF=AB=1,根据等腰直角三角形的性质即可得到结论.
【详解】解:过D作DF⊥AC于F,∴∠DFC=∠A=90°,∴AB∥DF,
∵点D是BC边的中点,∴BD=DC,∴AF=CF,∴DF=AB=1,
∵∠DEC=45°,∴△DEF是等腰直角三角形,∴DE=DF=,故答案为:.
【点睛】本题考查了三角形的中位线定理,平行线的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造等腰直角三角形是解题的关键.
12.(2021·桥柱中学八年级期末)如图,在正方形中,已知,点分别是边的中点,点F是边上的动点,连接,将正方形沿折叠,的对应点分别为,则线段的最小值是_____.
【答案】
【分析】如图,连接EG,EB′.求出EG,EB′的长,可以判定点B′在EG的延长线上时,GB′的值最小,最小值=,即可解决问题.
【详解】解:如图,连接EG,EB′,
∵四边形ABCD是正方形,∴∠A=∠D=90°,AD=DC=AB=2,
∵AE=DE=1,DG=GC=1,∴EG=
==,
由翻折的性质可知,∠A′=∠A=90°,A′E=AE=1,A′B′=AB=2,
∴EB′==
=,
∴当点B′在EG的延长线上时,GB′的值最小,最小值=,故答案为.
【点睛】本题考查正方形的性质,翻折变换,勾股定理等知识,解题的关键是学会用转化的思想思考问题,属于中考填空题中的压轴题.
13.(2020·浙江九年级)如图所示,把大正方形纸片剪成五个部分,在分别距离大正方形的四个顶点5厘米处沿方向剪开,中间的部分正好是小正方形,那么小正方形的面积是________平方厘米.
【答案】50
【分析】先判断出△ECP是等腰直角三角形,进而求出PE,再判断出四边形PEGH是矩形,进而求出GH,即可得出结论.
【详解】解:如图,∵四边形EFGH是正方形,∴∠G=90°,
过点P作PE∥FH交BC于E,∴∠PEC=∠HFC=45°,
∴∠CPE=90°-∠PEC=45°,∴CE=CP=5,∴PE=PC=,
∵∠DPQ=45°,∴∠EPQ=180°-∠CPE-∠DPQ=90°,∵阴影部分是正方形,∴∠PHG=∠EGH=90°,
∴四边形EPHG为矩形,∴GH=PE=,∴S阴影=GH2=()2=50,故答案为:50.
【点睛】此题主要考查了等腰三角形的判定和性质,平行线的性质,矩形的判定和性质,勾股定理,正方形的性质,求出PE是解本题的关键.
15.(2021·山东淄博市·八年级期末)如图,在菱形中,,,点是直线,之间任意一点,连接,,,,则和的面积之和是______.
【答案】12
【分析】连接BD,根据菱形对角线的性质,利用勾股定理计算BD的长,根据两平行线的距离相等,所以△EAB和△ECD的面积和等于菱形ABCD面积的一半,再利用菱形面积等于对角线积的一半计算可得结论.
【详解】如图,连接BD交AC于O,
∵四边形ABCD是菱形,∴AC⊥BD,OA=AC=×6=3,
∵AB=5,由勾股定理得:OB=,∴BD=2OB=8,
∵AB∥CD,∴△EAB和△ECD的高的和等于点C到直线AB的距离,
∴△EAB和△ECD的面积和=×=××AC×BD=.故答案为:12.
【点睛】本题考查菱形的性质,三角形的面积,平行线的性质,熟知平行线的距离相等,得△EAB和△ECD的高的和等于点C到直线AB的距离是解题的关键.
16.(2020·广州市广外附设外语学校九年级期中)如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2019次,点B的落点依次为B1,B2,B3,…,则B2019的坐标为_____.
【答案】(1346,0)
【分析】连接AC,根据条件可以求出AC,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2019=336×6+3,因此点B3向右平移1344(即336×4)即可到达点B2019,根据点B3的坐标就可求出点B2019的坐标.
【详解】解:连接AC,如图所示.∵四边形OABC是菱形,∴OA=AB=BC=OC.
∵∠ABC=60°,∴△ABC是等边三角形.∴AC=AB.∴AC=OA.
∵OA=1,∴AC=1.画出第5次、第6次、第7次翻转后的图形,如图所示.
由图可知:每翻转6次,图形向右平移4.
∵2019=336×6+3,∴点B3向右平移1344(即336×4)到点B2019.
∵B3的坐标为(2,0),∴B2019的坐标为(2+1344,0),∴B2019的坐标为(1346,0).
故答案为:(1346,0).
【点睛】本题考查了菱形的性质、等边三角形的判定与性质等知识,考查了操作、探究、发现规律的能力.发现“每翻转6次,图形向右平移4”是解决本题的关键.
17.(2021·黑龙江九年级期末)如图,在矩形中,,为中点,点为上一动点,将沿所在直线折叠到的位置,连接,则的最小值为__________.
【答案】
【分析】由题意可知当点G在DE上时,此时GD的值最小,根据勾股定理求出DE,根据折叠的性质可知GE=BE,即可求出GD的最小值.
【详解】
解:如图所示,
由EG=EB==,可得当点G在DE上时,此时GD的值最小,
根据折叠的性质,△EBF≌△EGF,∴EG⊥GF,∴EG=EB,
∵E是AB边的中点,AB=5,∴AE=EG=,
∵BC=AD=12,∴Rt△ADE中,DE=,∴GD=.故答案为:.
【点睛】本题主要考查折叠的性质、全等三角形的判定与性质的综合运用;注意掌握并确定点G在何位置时,GD的值最小是解决问题的关键.
18.(2020·浙江九年级期末)如图,在平行四边形中,,F是的中点,,垂足E在线段上.下列结论①;②;③;④中,一定成立的是_________.(请填序号)
【答案】②③④
【分析】如图延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.利用平行四边形的性质,全等三角形的判定和性质一一判断即可解决问题.
【详解】解:如图,延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.
∵四边形ABCD是平行四边形,∴AB∥CH,∴∠A=∠FDH,
在△AFE和△DFH中,,∴△AFE≌△DFH,∴EF=FH,
∵CE⊥AB,AB∥CH,
∴CE⊥CD,∴∠ECH=90°,∴CF=EF=FH,故②正确,
∵DF=CD=AF,∴∠DFC=∠DCF=∠FCB,
∵∠FCB>∠ECF,∴∠DCF>∠ECF,故①错误,
∵FK∥AB,FD∥CK,∴四边形DFKC是平行四边形,
∵AD=2CD,F是AD中点,∴DF=CD,∴四边形DFKC是菱形,∴∠DFC=∠KFC,
∵AE∥FK,∴∠AEF=∠EFK,∵FE=FC,FK⊥EC,∴∠EFK=∠KFC,
∴∠DFE=3∠AEF,故③正确,∵四边形EBCN是平行四边形,∴S△BEC=S△ENC,
∵S△EHC=2S△EFC,S△EHC>S△ENC,∴S△BEC<2S△CEF,故④正确,
故正确的有②③④.故答案为②③④.
【点睛】本题考查平行四边形的性质、全等三角形的判定和性质、直角三角形斜边的中线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·广东龙岭初级中学八年级月考)如图,在矩形ABCD中,AB=6,BC=10,点E在边CD上,连接AE,将四边形ABCE沿直线AE折叠,得到多边形,且恰好经过点D.
(1)线段DC′的长度;(2)求ADE的面积.
【答案】(1)2;(2)
【分析】(1)由矩形的性质可得AD=BC=10,AB=CD=6,∠B=∠C=90°,由折叠的性质可得AB=AB'=6,CE=C'E,B'C'=BC=10,∠B'=∠B=90°,∠C=∠C'=90°,由勾股定理可求B'D的长,可得C'D的长;
(2)设DE=x,则EC′=6-x,利用勾股定理列方程求解,从而可求三角形面积.
【详解】解:(1)∵四边形ABCD是矩形∴AD=BC=10,AB=CD=6,∠B=∠C=90°
∵将四边形ABCE沿直线AE折叠,得到多边形AB′C′E,
∴AB=AB'=6,CE=C'E,B'C'=BC=10,∠B'=∠B=90°,∠C=∠C'=90°
∵B'D=∴C'D=B'C'-B'D=2,
(2)设DE=x,则EC′=6-x,由(1)可知∠C'=90°,C'D=2
∴在Rt△C′DE中,,解得:∴ADE的面积为
【点睛】本题考查了折叠变换,矩形的性质,勾股定理,熟练运用折叠的性质是本题的关键.
20.(2021·贵州九年级期末)如图,已知四边形是平行四边形,E是延长线上一点且,连接,.(1)求证:四边形是平行四边形,(2)连接,若,,求的面积.
【答案】(1)见解析;(2)
【分析】(1)根据四边形是平行四边形,得到,,再根据,得到,利用一组对边平行且相等的四边形是平行四边形去判定.(2)先利用已知条件证四边形是菱形,再在中,利用勾股定理求BO,进而求BC,则可求菱形面积.
【详解】解:(1)∵四边形是平行四边形,∴,,
又∵,∴,,∴四边形是平行四边形.
(2)如图,连接,交于点O,∵,,
∴,由(1)得四边形是平行四边形,
∴是菱形,∴,
∵,∴,
在中,,
∴,∴.
【点睛】本题考查了平行四边形、菱形性质和判定的综合应用,熟练掌握相关知识是解答此题的关键.
21.(2020·浙江八年级期末)如图,在四边形中,,,,,,动点N从点D出发,以每秒的速度在射线上运动到C点返回,动点M从点A出发,在线段上,以每秒的速度向点B运动,点M,N分别从点A,D同时出发.当点M运动到点B时,点N随之停止运动,设运动时间为t(秒).(1)当t为何值时,四边形是平行四边形.(2)是否存在点N,使是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
【答案】(1)5秒或秒;(2)存在,秒或秒或秒
【分析】(1)由题意已知,AB∥CD,要使四边形MNBC是平行四边形,则只需要让BM=CN即可,因为M、N点的速度已知,AB、CD的长度已知,要求时间,用时间=路程÷速度,即可求出时间;
(2)使△BMN是等腰三角形,可分三种情况,即BM=BN、NM=NB、MN=MB;可利用等腰三角形及直角梯形的性质,分别用t表达等腰三角形的两腰长,再利用两腰相等即可求得时间t.
【详解】解:(1)设运动时间为t秒.∵四边形MNCB是平行四边形,∴MB=NC,
当N从D运动到C时,∵BC=13cm,CD=21cm,
∴BM=AB-AM=16-t,CN=21-2t,∴16-t=21-2t,解得t=5,
当N从C运动到D时,∵BM=AB-AM=16-t,CN=2t-21∴16-t=2t-21,解得t=,
∴当t=5秒或秒时,四边形MNCB是平行四边形;
(2)△NMB是等腰三角形有三种情况,
Ⅰ.当NM=NB时,作NH⊥AB于H,则HM=HB,
当N从D运动到C时,∵MH=HB=BM=(16-t),
由AH=DN得2t=(16?t)+t,解得t=秒;
当点N从C向D运动时,观察图象可知,只有由题意:42-2t=(16-t)+t,解得t=秒.
Ⅱ.当MN=MB,当N从D运动到C时,MH=AH-AM=DN-AM=2t-t=t,BM=16-t,
∵MN2=t2+122,∴(16-t)2=122+t2,解得t=(秒);
Ⅲ.当BM=BN,当N从C运动到D时,则BH=AB-AH=AB-DN=16-2t,
∵BM2=BN2=NH2+BH2=122+(16-2t)2,∴(16-t)2=122+(16-2t)2,即3t2-32t+144=0,
∵△<0,∴方程无实根,
综上可知,当t=秒或秒或秒时,△BMN是等腰三角形.
【点睛】本题主要考查了直角梯形的性质、平行四边形的性质、梯形的面积、等腰三角形的性质,特别应该注意要全面考虑各种情况,不要遗漏.
22.(2020·浙江丽水初三期末)如图,在菱形中,是边上的动点,作交于点,在上取点使,连结(1)求的度数;(2)求证:(3)若是的中点,当为何值时,是等腰三角形.
【答案】(1)120°;(2)见解析;(3)2
【分析】(1)由题意可证是等边三角形,可得,可求解;
(2)根据菱形的性质,等边三角形的性质,利用证明可证明结论;
(3)可分三种情况:当时;当时;当时分别进行计算即可求解.
【解析】解:(1),,是等边三角形,
,;
(2)证明:由(1)知,,
四边形为菱形,,,,
,,,,
是等边三角形,,,,
,,,
,;
(3),,
当时,,只有当时,,
此时,为,的中点,;
当时,在运动过程中,到达之前,永远在点下方,
从同一点引出的,再点下方不存在;
当时,点在的中垂线上,即点上,
而运动期间不可能位于线段上,在上不存在,
综上,,即当为2时,是等腰三角形.
【点睛】本题主要考查全等三角形的判定与性质,等腰三角形的性质,等边三角形的判定与性质,菱形的性质等知识的综合运用,注意分类讨论.
23.(2020·辽宁九年级期中)如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
【答案】(1)见解析;(2)四边形EPCF是平行四边形,理由见解析
【分析】(1)由正方形的性质可以得出AB=BC,∠ABP=∠ABC=∠90°,可以得出△PBA≌△FBC,再根据对边平行且相等的四边形是平行四边形就可以得出结论;
(2)由正方形的性质可以得出AB=BC,∠FBC=∠ABC=∠90°,可以得出△PBA≌△FBC,再根据对边平行且相等的四边形是平行四边形就可以得出结论.
【详解】(1)∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠PBA=90°
∵在△PBA和△FBC中,,∴△PBA≌△FBC(SAS),∴PA=FC,∠PAB=∠FCB.
∵PA=PE,∴PE=FC.∵∠PAB+∠APB=90°,∴∠FCB+∠APB=90°,
∵∠EPA=90°,∴∠APB+∠EPA+∠FCP=180°,
即∠EPC+∠PCF=180°,∴EP∥FC,∴四边形EPCF是平行四边形;
(2)结论:四边形EPCF是平行四边形,
∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠CBF=90°,
∵在△PBA和△FBC中,,∴△PBA≌△FBC(SAS),∴PA=FC,∠APB=∠BFC,
∵PA=PE,∴PE=FC,∵∠FCB+∠BFC=90°,∠BPE+∠APB=90°,
∴∠BPE=∠FCB,∴EP∥FC,∴四边形EPCF是平行四边形.
【点睛】本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,平行四边形的判定,解答时灵活运用平行四边形的判定方法是关键.
24.(2020·浙江八年级月考)定义,我们把对角线互相垂直的四边形叫做和美四边形,对角线交点作为和美四边形的中心.
(1)写出一种你学过的和美四边形______;
(2)顺次连接和美四边形四边中点所得四边形是(
)
A.矩形
B,菱形
C.正方形
D.无法确定
(3)如图1,点O是和美四边形的中心,分别是边的中点,连接,记四边形的面积为,用等式表示的数量关系(无需说明理由)
(4)如图2,四边形是和美四边形,若,求的长.
【答案】(1)正方形;(2)A;(3)S1+S3=S2+S4;(4)
【分析】(1)根据正方形的对角线互相垂直解答;(2)根据矩形的判定定理解答;
(3)根据三角形的中线把三角形分为面积相等的两部分解答;
(4)根据和美四边形的定义、勾股定理计算即可.
【详解】解:(1)正方形是学过的和美四边形,故答案为:正方形;
(2)顺次连接和美四边形四边中点所得四边形是矩形,
如图,四边形ACBD中,对角线AB⊥CD,即为“和美四边形”,
点E、F、G、H分别是AC、AD、BD、BC的中点,∴EF∥CD∥HG,且EF=HG=CD,
EH∥FG∥AB,且EH=FG=AB,∴四边形EFGH为平行四边形,
∵AB⊥CD,∴EF⊥EH,∴平行四边形EFGH是矩形;故选:A.
(3)连接AC和BD,由和美四边形的定义可知,AC⊥BD,
则∠AOB=∠BOC=∠COD=∠DOA=90°,
又E、F、G、H分别是边AB、BC、CD、DA的中点,
∴△AOE的面积=△BOE的面积,△BOF的面积=△COF的面积,△COG的面积=△DOG的面积,△DOH的面积=△AOH的面积,
∴S1+S3=△AOE的面积+△COF的面积+△COG的面积+△AOH的面积=S2+S4;
(4)如图,连接AC、BD交于点O,则AC⊥BD,
∵在Rt△AOB中,AO2=AB2-BO2,
Rt△DOC中,DO2=DC2-CO2,AB=4,BC=2,CD=5,
∴可得AD2=AO2+DO2=AB2-BO2+DC2-CO2=AB2+DC2-BC2=42+52-22=37,
即可得.
【点睛】本题考查的是和美四边形的定义、矩形的判定、勾股定理的应用,正确理解和美四边形的定义、掌握矩形的判定定理是解题的关键.
25.(2020·吉林省初三一模)(教材呈现)如图是八年级下册数学教材第117页的部分内容.
结合图①,补全证明过程.
(应用)如图②,直线EF分别交矩形ABCD的边AD、BC于点E、F,将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=3,BC=4,则四边形ABFE的周长为
.
(拓展)如图③,直线EF分别交?ABCD的边AD、BC于点E、F,将?ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=,BC=4,∠C=45°,则EF的长为
.
【答案】【教材呈现】证明见解析;【应用】;【拓展】;
【分析】教材呈现:由“ASA”可证△AOE≌△COF,可得OE=OF,由对角线互相平分的四边形是平行四边形可证四边形AFCE是平行四边形,即可证平行四边形AFCE是菱形;
应用:过点F作FH⊥AD于H,由折叠的性质可得AF=CF,∠AFE=∠EFC,由勾股定理可求BF的长,EF的长,拓展:过点A作AN⊥BC,交CB的延长线于N,过点F作FM⊥AD于M,由等腰直角三角形的性质可求AN=BN=2,由勾股定理可求AE=AF=,再利用勾股定理可求EF的长.
【解析】解:【教材呈现】∵四边形ABCD是矩形,∴AE∥CF,∴∠EAO=∠FCO,
∵EF垂直平分AC,∴AO=CO,∠AOE=∠COF=90°,∴△AOE≌△COF(ASA)∴OE=OF,
又∵AO=CO,∴四边形AFCE是平行四边形,
∵EF⊥AC,∴平行四边形AFCE是菱形;
【应用】如图,过点F作FH⊥AD于H,
∵将矩形ABCD沿EF翻折,使点C的对称点与点A重合,∴AF=CF,∠AFE=∠EFC,
∵AF2=BF2+AB2,∴(4﹣BF)2=BF2+9,∴BF=,∴AF=CF=,
∵AD∥BC,∴∠AEF=∠EFC=∠AFE,∴AE=AF=,
∵∠B=∠BAD=∠AHF=90°,∴四边形ABFH是矩形,
∴AB=FH=3,AH=BF=,∴EH=,∴EF===,
∴四边形ABFE的周长=AB+BF+AE+EF=3+++=,故答案为:.
【拓展】如图,过点A作AN⊥BC,交CB的延长线于N,过点F作FM⊥AD于M,
∵四边形ABCD是平行四边形,∠C=45°,∴∠ABC=135°,∴∠ABN=45°,
∵AN⊥BC,∴∠ABN=∠BAN=45°,∴AN=BN=AB=2,
∵将?ABCD沿EF翻折,使点C的对称点与点A重合,∴AF=CF,∠AFE=∠EFC,
∵AD∥BC,∴∠AEF=∠EFC=∠AFE,∴AE=AF,
∵AF2=AN2+NF2,∴AF2=4+(6﹣AF)2,∴AF=,∴AE=AF=,
∵AN∥MF,AD∥BC,∴四边形ANFM是平行四边形,
∵AN⊥BC,∴四边形ANFM是矩形,∴AN=MF=2,∴AM===,
∴ME=AE﹣AM=,∴EF===,故答案为:.
【点睛】本题是四边形综合题,考查了平行四边形的性质,菱形的性质,折叠的性质,全等三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造直角三角形是本题的关键.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教版八年级下册数学
单元测评培优卷(原版+解析版)
第18章
平行四边形
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·成都市初三期末)下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
2.(2021·广东八年级期末)如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
3.(2020·温州外国语学校八年级月考)从①;②;③;④.这四个条件中选取两个,使四边形成为平行四边形.下面不能说明是平行四边形的是(
)
A.①②
B.①③
C.②④
D.①④
4.(2021·陕西九年级期末)如图,矩形的对角线,相交于点,,若的周长比的周长大10,则的长为(
).
A.
B.
C.10
D.20
5.(2020·江西新余初三期末)如图,在任意四边形中,,,,分别是,,,上的点,对于四边形的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是(
)
A.当,,,是各边中点,且时,四边形为菱形
B.当,,,是各边中点,且时,四边形为矩形
C.当,,,不是各边中点时,四边形可以为平行四边形
D.当,,,不是各边中点时,四边形不可能为菱形
6.(2020·湖北九年级期末)如图,在中,,,,依据尺规作图的痕迹,则的面积为(
)
A.12
B.
C.
D.
7.(2020·无锡市前洲中学初三月考)如图,在菱形中对角线相交于点,直线交
于点,则的长(
)
A.4
B.4.
8
C.2.
4
D.3.
2
8.(2021·浙江八年级期末)图1中甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD.已知图甲中,,,图乙中
,则图2中正方形的对角线AC长为( )
A.
B.
C.
D.
9.(2020·佳木斯市九年级期中)如图,点是正方形内一点,,,,则的长为(
)
A.
B.
C.
D.
10.(2020·浙江八年级期中)如图,以平行四边形的边、、、为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形,当时,有以下结论:①;②;③;④;⑤四边形是平行四边形.则结论正确的是(
)
A.①③④
B.②③⑤
C.①③④⑤
D.②③④⑤
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·浙江八年级)如图,在中,,,点D是边的中点,点E在边上,若,那么的长是__________.
12.(2021·桥柱中学八年级期末)如图,在正方形中,已知,点分别是边的中点,点F是边上的动点,连接,将正方形沿折叠,的对应点分别为,则线段的最小值是_____.
13.(2020·浙江九年级)如图所示,把大正方形纸片剪成五个部分,在分别距离大正方形的四个顶点5厘米处沿方向剪开,中间的部分正好是小正方形,那么小正方形的面积是________平方厘米.
15.(2021·山东淄博市·八年级期末)如图,在菱形中,,,点是直线,之间任意一点,连接,,,,则和的面积之和是______.
16.(2020·广州市广外附设外语学校九年级期中)如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2019次,点B的落点依次为B1,B2,B3,…,则B2019的坐标为_____.
17.(2021·黑龙江九年级期末)如图,在矩形中,,为中点,点为上一动点,将沿所在直线折叠到的位置,连接,则的最小值为__________.
18.(2020·浙江九年级期末)如图,在平行四边形中,,F是的中点,,垂足E在线段上.下列结论①;②;③;④中,一定成立的是_________.(请填序号)
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·广东龙岭初级中学八年级月考)如图,在矩形ABCD中,AB=6,BC=10,点E在边CD上,连接AE,将四边形ABCE沿直线AE折叠,得到多边形,且恰好经过点D.
(1)线段DC′的长度;(2)求ADE的面积.
20.(2021·贵州九年级期末)如图,已知四边形是平行四边形,E是延长线上一点且,连接,.(1)求证:四边形是平行四边形,(2)连接,若,,求的面积.
21.(2020·浙江八年级期末)如图,在四边形中,,,,,,动点N从点D出发,以每秒的速度在射线上运动到C点返回,动点M从点A出发,在线段上,以每秒的速度向点B运动,点M,N分别从点A,D同时出发.当点M运动到点B时,点N随之停止运动,设运动时间为t(秒).(1)当t为何值时,四边形是平行四边形.(2)是否存在点N,使是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
22.(2020·浙江丽水初三期末)如图,在菱形中,是边上的动点,作交于点,在上取点使,连结(1)求的度数;(2)求证:(3)若是的中点,当为何值时,是等腰三角形.
23.(2020·辽宁九年级期中)如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
24.(2020·浙江八年级月考)定义,我们把对角线互相垂直的四边形叫做和美四边形,对角线交点作为和美四边形的中心.
(1)写出一种你学过的和美四边形______;
(2)顺次连接和美四边形四边中点所得四边形是(
)
A.矩形
B,菱形
C.正方形
D.无法确定
(3)如图1,点O是和美四边形的中心,分别是边的中点,连接,记四边形的面积为,用等式表示的数量关系(无需说明理由)
(4)如图2,四边形是和美四边形,若,求的长.
25.(2020·吉林省初三一模)(教材呈现)如图是八年级下册数学教材第117页的部分内容.
结合图①,补全证明过程.
(应用)如图②,直线EF分别交矩形ABCD的边AD、BC于点E、F,将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=3,BC=4,则四边形ABFE的周长为
.
(拓展)如图③,直线EF分别交?ABCD的边AD、BC于点E、F,将?ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=,BC=4,∠C=45°,则EF的长为
.
2020-2021学年人教版八年级下册数学
单元测评培优卷(原版+解析版)
第18章
平行四边形
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·成都市初三期末)下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
【答案】D
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解析】A、一组对边平行,另一组对边相等的四边形有可能是等腰梯形,故A选项错误;
B、对角线互相垂直的四边形也可能是一般四边形,故B选项错误;
C、对角线相等的四边形有可能是等腰梯形,故C选项错误.
D、一组邻边相等的矩形是正方形,故D选项正确.故选D.
【点睛】本题考查特殊平行四边形的判定,需熟练掌握各特殊四边形的特点.
2.(2021·广东八年级期末)如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
【答案】B
【分析】根据三角形中位线定理解答即可.
【详解】解:∵点D和点E分别是BC和BA的中点,
∴DE是△ABC的中位线,∴DE=AC=4=2,故选:B.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
3.(2020·温州外国语学校八年级月考)从①;②;③;④.这四个条件中选取两个,使四边形成为平行四边形.下面不能说明是平行四边形的是(
)
A.①②
B.①③
C.②④
D.①④
【答案】D
【分析】根据平行四边形的判定方法逐项判断即可.
【详解】解:A、选①②,即四边形ABCD满足,,根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD是平行四边形,故本选项不符合题意;
B、选①③,即四边形ABCD满足,,根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD是平行四边形,故本选项不符合题意;
C、选②④,即四边形ABCD满足,,根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD是平行四边形,故本选项不符合题意;
D、选①④,即四边形ABCD满足,,一组对边平行,另一组对边相等,不能判定四边形ABCD是平行四边形,故本选项符合题意.故选:D.
【点睛】本题考查了平行四边形的判定,属于基础题型,熟知平行四边形的判定方法是正确判断的关键.
4.(2021·陕西九年级期末)如图,矩形的对角线,相交于点,,若的周长比的周长大10,则的长为(
).
A.
B.
C.10
D.20
【答案】A
【分析】由矩形的性质和已知条件求出AB=BC,BC=10,即可得出答案.
【详解】解:∵四边形ABCD是矩形,∴AO=CO=DO=BO,AD=BC,∠ABC=90°,AB∥CD,
∴∠BAC=∠ACD=30°,∴AB=BC,
∵△ABC的周长=AB+AC+BC=AB+AO+OC+BC,△AOB的周长=AB+AO+BO,
又∵ABC的周长比△AOB的周长长10,
∴AB+AC+BC-(AB+AO+BO)=BC=10,∴AB=BC=;故选:A.
【点睛】本题考查了矩形的性质、含30°角的直角三角形的性质等知识,熟练掌握矩形的性质,求出BC的长是解题的关键.
5.(2020·江西新余初三期末)如图,在任意四边形中,,,,分别是,,,上的点,对于四边形的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是(
)
A.当,,,是各边中点,且时,四边形为菱形
B.当,,,是各边中点,且时,四边形为矩形
C.当,,,不是各边中点时,四边形可以为平行四边形
D.当,,,不是各边中点时,四边形不可能为菱形
【答案】D
【分析】当E,F,G,H是四边形ABCD各边中点时,连接AC、BD,如图,根据三角形的中位线定理可得四边形EFGH是平行四边形,然后根据菱形的定义和矩形的定义即可对A、B两项进行判断;画出符合题意的平行四边形,但满足,,,不是各边中点即可判断C项;画出符合题意的菱形,但满足,,,不是各边中点即可判断D项,进而可得答案.
【解析】A.当E,F,G,H是四边形ABCD各边中点时,连接AC、BD,如图,则由三角形的中位线定理得:EH=BD,EH∥BD;FG=BD,FG∥BD,所以EH=FG,EH∥FG,即四边形EFGH是平行四边形;
当AC=BD时,∵EH=BD,EF=AC,∴EF=EH,故四边形EFGH为菱形,故A正确;
B.当E,F,G,H是四边形ABCD各边中点,且AC⊥BD时,如上图,由三角形的中位线定理可得:EH∥BD,EF∥AC,所以EH⊥EF,故平行四边形EFGH为矩形,故B正确;
C.如图所示,若EF∥HG,EF=HG,则四边形EFGH为平行四边形,此时E,F,G,H不是四边形ABCD各边中点,故C正确;
D.如图所示,若EF=FG=GH=HE,则四边形EFGH为菱形,此时E,F,G,H不是四边形ABCD各边中点,故D错误;故选:D.
【点睛】本题考查了中点四边形以及特殊四边形的判定等知识,熟练掌握中点四边形的形状、会画出符合题意的反例图形是解题关键.
6.(2020·湖北九年级期末)如图,在中,,,,依据尺规作图的痕迹,则的面积为(
)
A.12
B.
C.
D.
【答案】C
【分析】由作图痕迹可得EF为AB的中垂线,结合判断出△ABE为等边三角形,从而结合边长求出在BC边上的高为,再根据比例关系求得BC的长度,最终计算面积即可.
【详解】设尺规作图所得直线与AB交于F点,根据题意可得EF为AB的中垂线,∴AE=BE,
又∵,∴△ABE为等边三角形,边长AB=CD=4,∴BF=2,BE=4,,∴在BC边上的高为,
又∵,BE=4,∴EC=2,BC=2+4=6,
∴=×6=,故选:C.
【点睛】本题考查平行四边形的性质,中垂线的识别与性质,以及等边三角形的判定与性质,准确根据作图痕迹总结出等边三角形是解题关键.
7.(2020·无锡市前洲中学初三月考)如图,在菱形中对角线相交于点,直线交
于点,则的长(
)
A.4
B.4.
8
C.2.
4
D.3.
2
【答案】D
【分析】根据菱形的性质可得AC⊥DB,AO=,BO=,然后利用勾股定理计算出AB长,再根据菱形的面积公式得到S菱形ABCD=,进而得到△AOB的面积,然后根据直角三角形的面积计算出EO长,再利用勾股定理求出AE即可.
【解析】解:∵四边形ABCD是菱形,
∴AC⊥DB,AO=,BO=
∵AC=8,BD=6,∴AO=4,BO=3,S菱形ABCD=
∴AB=,S△AOB=6,即∴EO=,
在Rt△AOE中,,故选:D.
【点睛】此题主要考查了菱形的性质、面积、以及勾股定理,关键是掌握菱形的两条对角线互相垂直.
8.(2021·浙江八年级期末)图1中甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD.已知图甲中,,,图乙中
,则图2中正方形的对角线AC长为( )
A.
B.
C.
D.
【答案】D
【分析】连接,过点作交于点,根据甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD,可得是等腰直角三角形,则可求得,,根据勾股定理,可得:,,则有,,根据正方形的对角线可求出答案.
【详解】解:如图示,连接,过点作交于点,
∵甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD.
∴根据题意,根据对称性可得是等腰直角三角形,则有:,
∵,,∴,,
又∵,,∴根据勾股定理,可得:,,
则有,∴,
∴正方形的对角线,故选:D.
【点睛】本题考查了正方形的性质,勾股定理,直角三角形的性质,熟悉相关性质是解题的关键.
9.(2020·佳木斯市九年级期中)如图,点是正方形内一点,,,,则的长为(
)
A.
B.
C.
D.
【答案】C
【分析】将绕着点A顺时针旋转90°得到,连接,则是等腰直角三角形,,然后根据勾股定理即可得到结论.
【详解】将绕着点A顺时针旋转90°得到,连接,则是等腰直角三角形
∴∴,∴
∵∴∴故选C.
【点睛】本题考查了正方形的性质,旋转的性质,等腰直角三角形的判定和性质,和勾股定理,正确的作出辅助线是本题的关键.
10.(2020·浙江八年级期中)如图,以平行四边形的边、、、为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形,当时,有以下结论:①;②;③;④;⑤四边形是平行四边形.则结论正确的是(
)
A.①③④
B.②③⑤
C.①③④⑤
D.②③④⑤
【答案】D
【分析】根据平行四边形性质得出∠ABC=∠ADC=α,∠BAD=∠BCD,AB=CD,AD=BC,AD∥BC,AB∥CD,根据等腰直角三角形得出BE=AE=CG=DG,AH=DH=BF=CF,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠EDA=45°,求出∠HAE=∠HDG=∠FCG=∠FBE=90°+α,证△FBE≌△HAE≌△HDG≌△FCG,推出∠BFE=∠GFC,EF=EH=HG=GF,求出∠EFG=90°,根据正方形性质得出即可.
【详解】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=α,∠BAD=∠BCD,AB=CD,AD=BC,AD∥BC,AB∥CD,
∵平行四边形ABCD的边AB、BC、CD、DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,∴BE=AE=CG=DG,AH=DH=BF=CF,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠EDA=45°,∵AB∥CD,∴∠BAD=∠BCD=180°-α,
∴∠EAH=360°-45°-45°-(180°-α)=90°+α,∠GCF=360°-45°-45°-(180°-α)=90°+α,
∴①错误;②正确;∠HDG=45°+45°+α=90°+α,∠FBE=45°+45°+α=90°+α,
∴∠HAE=∠HDG=∠FCG=∠FBE,在△FBE、△HAE、△HDG、△FCG中,
,∴△FBE≌△HAE≌△HDG≌△FCG(SAS),
∴∠BFE=∠GFC,EF=EH=HG=GF,③正确;∴四边形EFGH是菱形,
∵∠BFC=90°=∠BFE+∠EFC=∠GFC+∠CFE,∴∠EFG=90°,
∴四边形EFGH是正方形,⑤正确;∴EH⊥GH,④正确;故选:D.
【点睛】本题考查了等腰直角三角形,全等三角形的性质和判定,正方形的判定,平行四边形的性质,菱形的判定的应用,主要考查学生的推理能力.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·浙江八年级)如图,在中,,,点D是边的中点,点E在边上,若,那么的长是__________.
【答案】
【分析】过D作DF⊥AC于F,得到AB∥DF,求得AF=CF,根据三角形中位线定理得到DF=AB=1,根据等腰直角三角形的性质即可得到结论.
【详解】解:过D作DF⊥AC于F,∴∠DFC=∠A=90°,∴AB∥DF,
∵点D是BC边的中点,∴BD=DC,∴AF=CF,∴DF=AB=1,
∵∠DEC=45°,∴△DEF是等腰直角三角形,∴DE=DF=,故答案为:.
【点睛】本题考查了三角形的中位线定理,平行线的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造等腰直角三角形是解题的关键.
12.(2021·桥柱中学八年级期末)如图,在正方形中,已知,点分别是边的中点,点F是边上的动点,连接,将正方形沿折叠,的对应点分别为,则线段的最小值是_____.
【答案】
【分析】如图,连接EG,EB′.求出EG,EB′的长,可以判定点B′在EG的延长线上时,GB′的值最小,最小值=,即可解决问题.
【详解】解:如图,连接EG,EB′,
∵四边形ABCD是正方形,∴∠A=∠D=90°,AD=DC=AB=2,
∵AE=DE=1,DG=GC=1,∴EG=
==,
由翻折的性质可知,∠A′=∠A=90°,A′E=AE=1,A′B′=AB=2,
∴EB′==
=,
∴当点B′在EG的延长线上时,GB′的值最小,最小值=,故答案为.
【点睛】本题考查正方形的性质,翻折变换,勾股定理等知识,解题的关键是学会用转化的思想思考问题,属于中考填空题中的压轴题.
13.(2020·浙江九年级)如图所示,把大正方形纸片剪成五个部分,在分别距离大正方形的四个顶点5厘米处沿方向剪开,中间的部分正好是小正方形,那么小正方形的面积是________平方厘米.
【答案】50
【分析】先判断出△ECP是等腰直角三角形,进而求出PE,再判断出四边形PEGH是矩形,进而求出GH,即可得出结论.
【详解】解:如图,∵四边形EFGH是正方形,∴∠G=90°,
过点P作PE∥FH交BC于E,∴∠PEC=∠HFC=45°,
∴∠CPE=90°-∠PEC=45°,∴CE=CP=5,∴PE=PC=,
∵∠DPQ=45°,∴∠EPQ=180°-∠CPE-∠DPQ=90°,∵阴影部分是正方形,∴∠PHG=∠EGH=90°,
∴四边形EPHG为矩形,∴GH=PE=,∴S阴影=GH2=()2=50,故答案为:50.
【点睛】此题主要考查了等腰三角形的判定和性质,平行线的性质,矩形的判定和性质,勾股定理,正方形的性质,求出PE是解本题的关键.
15.(2021·山东淄博市·八年级期末)如图,在菱形中,,,点是直线,之间任意一点,连接,,,,则和的面积之和是______.
【答案】12
【分析】连接BD,根据菱形对角线的性质,利用勾股定理计算BD的长,根据两平行线的距离相等,所以△EAB和△ECD的面积和等于菱形ABCD面积的一半,再利用菱形面积等于对角线积的一半计算可得结论.
【详解】如图,连接BD交AC于O,
∵四边形ABCD是菱形,∴AC⊥BD,OA=AC=×6=3,
∵AB=5,由勾股定理得:OB=,∴BD=2OB=8,
∵AB∥CD,∴△EAB和△ECD的高的和等于点C到直线AB的距离,
∴△EAB和△ECD的面积和=×=××AC×BD=.故答案为:12.
【点睛】本题考查菱形的性质,三角形的面积,平行线的性质,熟知平行线的距离相等,得△EAB和△ECD的高的和等于点C到直线AB的距离是解题的关键.
16.(2020·广州市广外附设外语学校九年级期中)如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2019次,点B的落点依次为B1,B2,B3,…,则B2019的坐标为_____.
【答案】(1346,0)
【分析】连接AC,根据条件可以求出AC,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2019=336×6+3,因此点B3向右平移1344(即336×4)即可到达点B2019,根据点B3的坐标就可求出点B2019的坐标.
【详解】解:连接AC,如图所示.∵四边形OABC是菱形,∴OA=AB=BC=OC.
∵∠ABC=60°,∴△ABC是等边三角形.∴AC=AB.∴AC=OA.
∵OA=1,∴AC=1.画出第5次、第6次、第7次翻转后的图形,如图所示.
由图可知:每翻转6次,图形向右平移4.
∵2019=336×6+3,∴点B3向右平移1344(即336×4)到点B2019.
∵B3的坐标为(2,0),∴B2019的坐标为(2+1344,0),∴B2019的坐标为(1346,0).
故答案为:(1346,0).
【点睛】本题考查了菱形的性质、等边三角形的判定与性质等知识,考查了操作、探究、发现规律的能力.发现“每翻转6次,图形向右平移4”是解决本题的关键.
17.(2021·黑龙江九年级期末)如图,在矩形中,,为中点,点为上一动点,将沿所在直线折叠到的位置,连接,则的最小值为__________.
【答案】
【分析】由题意可知当点G在DE上时,此时GD的值最小,根据勾股定理求出DE,根据折叠的性质可知GE=BE,即可求出GD的最小值.
【详解】
解:如图所示,
由EG=EB==,可得当点G在DE上时,此时GD的值最小,
根据折叠的性质,△EBF≌△EGF,∴EG⊥GF,∴EG=EB,
∵E是AB边的中点,AB=5,∴AE=EG=,
∵BC=AD=12,∴Rt△ADE中,DE=,∴GD=.故答案为:.
【点睛】本题主要考查折叠的性质、全等三角形的判定与性质的综合运用;注意掌握并确定点G在何位置时,GD的值最小是解决问题的关键.
18.(2020·浙江九年级期末)如图,在平行四边形中,,F是的中点,,垂足E在线段上.下列结论①;②;③;④中,一定成立的是_________.(请填序号)
【答案】②③④
【分析】如图延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.利用平行四边形的性质,全等三角形的判定和性质一一判断即可解决问题.
【详解】解:如图,延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.
∵四边形ABCD是平行四边形,∴AB∥CH,∴∠A=∠FDH,
在△AFE和△DFH中,,∴△AFE≌△DFH,∴EF=FH,
∵CE⊥AB,AB∥CH,
∴CE⊥CD,∴∠ECH=90°,∴CF=EF=FH,故②正确,
∵DF=CD=AF,∴∠DFC=∠DCF=∠FCB,
∵∠FCB>∠ECF,∴∠DCF>∠ECF,故①错误,
∵FK∥AB,FD∥CK,∴四边形DFKC是平行四边形,
∵AD=2CD,F是AD中点,∴DF=CD,∴四边形DFKC是菱形,∴∠DFC=∠KFC,
∵AE∥FK,∴∠AEF=∠EFK,∵FE=FC,FK⊥EC,∴∠EFK=∠KFC,
∴∠DFE=3∠AEF,故③正确,∵四边形EBCN是平行四边形,∴S△BEC=S△ENC,
∵S△EHC=2S△EFC,S△EHC>S△ENC,∴S△BEC<2S△CEF,故④正确,
故正确的有②③④.故答案为②③④.
【点睛】本题考查平行四边形的性质、全等三角形的判定和性质、直角三角形斜边的中线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·广东龙岭初级中学八年级月考)如图,在矩形ABCD中,AB=6,BC=10,点E在边CD上,连接AE,将四边形ABCE沿直线AE折叠,得到多边形,且恰好经过点D.
(1)线段DC′的长度;(2)求ADE的面积.
【答案】(1)2;(2)
【分析】(1)由矩形的性质可得AD=BC=10,AB=CD=6,∠B=∠C=90°,由折叠的性质可得AB=AB'=6,CE=C'E,B'C'=BC=10,∠B'=∠B=90°,∠C=∠C'=90°,由勾股定理可求B'D的长,可得C'D的长;
(2)设DE=x,则EC′=6-x,利用勾股定理列方程求解,从而可求三角形面积.
【详解】解:(1)∵四边形ABCD是矩形∴AD=BC=10,AB=CD=6,∠B=∠C=90°
∵将四边形ABCE沿直线AE折叠,得到多边形AB′C′E,
∴AB=AB'=6,CE=C'E,B'C'=BC=10,∠B'=∠B=90°,∠C=∠C'=90°
∵B'D=∴C'D=B'C'-B'D=2,
(2)设DE=x,则EC′=6-x,由(1)可知∠C'=90°,C'D=2
∴在Rt△C′DE中,,解得:∴ADE的面积为
【点睛】本题考查了折叠变换,矩形的性质,勾股定理,熟练运用折叠的性质是本题的关键.
20.(2021·贵州九年级期末)如图,已知四边形是平行四边形,E是延长线上一点且,连接,.(1)求证:四边形是平行四边形,(2)连接,若,,求的面积.
【答案】(1)见解析;(2)
【分析】(1)根据四边形是平行四边形,得到,,再根据,得到,利用一组对边平行且相等的四边形是平行四边形去判定.(2)先利用已知条件证四边形是菱形,再在中,利用勾股定理求BO,进而求BC,则可求菱形面积.
【详解】解:(1)∵四边形是平行四边形,∴,,
又∵,∴,,∴四边形是平行四边形.
(2)如图,连接,交于点O,∵,,
∴,由(1)得四边形是平行四边形,
∴是菱形,∴,
∵,∴,
在中,,
∴,∴.
【点睛】本题考查了平行四边形、菱形性质和判定的综合应用,熟练掌握相关知识是解答此题的关键.
21.(2020·浙江八年级期末)如图,在四边形中,,,,,,动点N从点D出发,以每秒的速度在射线上运动到C点返回,动点M从点A出发,在线段上,以每秒的速度向点B运动,点M,N分别从点A,D同时出发.当点M运动到点B时,点N随之停止运动,设运动时间为t(秒).(1)当t为何值时,四边形是平行四边形.(2)是否存在点N,使是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
【答案】(1)5秒或秒;(2)存在,秒或秒或秒
【分析】(1)由题意已知,AB∥CD,要使四边形MNBC是平行四边形,则只需要让BM=CN即可,因为M、N点的速度已知,AB、CD的长度已知,要求时间,用时间=路程÷速度,即可求出时间;
(2)使△BMN是等腰三角形,可分三种情况,即BM=BN、NM=NB、MN=MB;可利用等腰三角形及直角梯形的性质,分别用t表达等腰三角形的两腰长,再利用两腰相等即可求得时间t.
【详解】解:(1)设运动时间为t秒.∵四边形MNCB是平行四边形,∴MB=NC,
当N从D运动到C时,∵BC=13cm,CD=21cm,
∴BM=AB-AM=16-t,CN=21-2t,∴16-t=21-2t,解得t=5,
当N从C运动到D时,∵BM=AB-AM=16-t,CN=2t-21∴16-t=2t-21,解得t=,
∴当t=5秒或秒时,四边形MNCB是平行四边形;
(2)△NMB是等腰三角形有三种情况,
Ⅰ.当NM=NB时,作NH⊥AB于H,则HM=HB,
当N从D运动到C时,∵MH=HB=BM=(16-t),
由AH=DN得2t=(16?t)+t,解得t=秒;
当点N从C向D运动时,观察图象可知,只有由题意:42-2t=(16-t)+t,解得t=秒.
Ⅱ.当MN=MB,当N从D运动到C时,MH=AH-AM=DN-AM=2t-t=t,BM=16-t,
∵MN2=t2+122,∴(16-t)2=122+t2,解得t=(秒);
Ⅲ.当BM=BN,当N从C运动到D时,则BH=AB-AH=AB-DN=16-2t,
∵BM2=BN2=NH2+BH2=122+(16-2t)2,∴(16-t)2=122+(16-2t)2,即3t2-32t+144=0,
∵△<0,∴方程无实根,
综上可知,当t=秒或秒或秒时,△BMN是等腰三角形.
【点睛】本题主要考查了直角梯形的性质、平行四边形的性质、梯形的面积、等腰三角形的性质,特别应该注意要全面考虑各种情况,不要遗漏.
22.(2020·浙江丽水初三期末)如图,在菱形中,是边上的动点,作交于点,在上取点使,连结(1)求的度数;(2)求证:(3)若是的中点,当为何值时,是等腰三角形.
【答案】(1)120°;(2)见解析;(3)2
【分析】(1)由题意可证是等边三角形,可得,可求解;
(2)根据菱形的性质,等边三角形的性质,利用证明可证明结论;
(3)可分三种情况:当时;当时;当时分别进行计算即可求解.
【解析】解:(1),,是等边三角形,
,;
(2)证明:由(1)知,,
四边形为菱形,,,,
,,,,
是等边三角形,,,,
,,,
,;
(3),,
当时,,只有当时,,
此时,为,的中点,;
当时,在运动过程中,到达之前,永远在点下方,
从同一点引出的,再点下方不存在;
当时,点在的中垂线上,即点上,
而运动期间不可能位于线段上,在上不存在,
综上,,即当为2时,是等腰三角形.
【点睛】本题主要考查全等三角形的判定与性质,等腰三角形的性质,等边三角形的判定与性质,菱形的性质等知识的综合运用,注意分类讨论.
23.(2020·辽宁九年级期中)如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
【答案】(1)见解析;(2)四边形EPCF是平行四边形,理由见解析
【分析】(1)由正方形的性质可以得出AB=BC,∠ABP=∠ABC=∠90°,可以得出△PBA≌△FBC,再根据对边平行且相等的四边形是平行四边形就可以得出结论;
(2)由正方形的性质可以得出AB=BC,∠FBC=∠ABC=∠90°,可以得出△PBA≌△FBC,再根据对边平行且相等的四边形是平行四边形就可以得出结论.
【详解】(1)∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠PBA=90°
∵在△PBA和△FBC中,,∴△PBA≌△FBC(SAS),∴PA=FC,∠PAB=∠FCB.
∵PA=PE,∴PE=FC.∵∠PAB+∠APB=90°,∴∠FCB+∠APB=90°,
∵∠EPA=90°,∴∠APB+∠EPA+∠FCP=180°,
即∠EPC+∠PCF=180°,∴EP∥FC,∴四边形EPCF是平行四边形;
(2)结论:四边形EPCF是平行四边形,
∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠CBF=90°,
∵在△PBA和△FBC中,,∴△PBA≌△FBC(SAS),∴PA=FC,∠APB=∠BFC,
∵PA=PE,∴PE=FC,∵∠FCB+∠BFC=90°,∠BPE+∠APB=90°,
∴∠BPE=∠FCB,∴EP∥FC,∴四边形EPCF是平行四边形.
【点睛】本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,平行四边形的判定,解答时灵活运用平行四边形的判定方法是关键.
24.(2020·浙江八年级月考)定义,我们把对角线互相垂直的四边形叫做和美四边形,对角线交点作为和美四边形的中心.
(1)写出一种你学过的和美四边形______;
(2)顺次连接和美四边形四边中点所得四边形是(
)
A.矩形
B,菱形
C.正方形
D.无法确定
(3)如图1,点O是和美四边形的中心,分别是边的中点,连接,记四边形的面积为,用等式表示的数量关系(无需说明理由)
(4)如图2,四边形是和美四边形,若,求的长.
【答案】(1)正方形;(2)A;(3)S1+S3=S2+S4;(4)
【分析】(1)根据正方形的对角线互相垂直解答;(2)根据矩形的判定定理解答;
(3)根据三角形的中线把三角形分为面积相等的两部分解答;
(4)根据和美四边形的定义、勾股定理计算即可.
【详解】解:(1)正方形是学过的和美四边形,故答案为:正方形;
(2)顺次连接和美四边形四边中点所得四边形是矩形,
如图,四边形ACBD中,对角线AB⊥CD,即为“和美四边形”,
点E、F、G、H分别是AC、AD、BD、BC的中点,∴EF∥CD∥HG,且EF=HG=CD,
EH∥FG∥AB,且EH=FG=AB,∴四边形EFGH为平行四边形,
∵AB⊥CD,∴EF⊥EH,∴平行四边形EFGH是矩形;故选:A.
(3)连接AC和BD,由和美四边形的定义可知,AC⊥BD,
则∠AOB=∠BOC=∠COD=∠DOA=90°,
又E、F、G、H分别是边AB、BC、CD、DA的中点,
∴△AOE的面积=△BOE的面积,△BOF的面积=△COF的面积,△COG的面积=△DOG的面积,△DOH的面积=△AOH的面积,
∴S1+S3=△AOE的面积+△COF的面积+△COG的面积+△AOH的面积=S2+S4;
(4)如图,连接AC、BD交于点O,则AC⊥BD,
∵在Rt△AOB中,AO2=AB2-BO2,
Rt△DOC中,DO2=DC2-CO2,AB=4,BC=2,CD=5,
∴可得AD2=AO2+DO2=AB2-BO2+DC2-CO2=AB2+DC2-BC2=42+52-22=37,
即可得.
【点睛】本题考查的是和美四边形的定义、矩形的判定、勾股定理的应用,正确理解和美四边形的定义、掌握矩形的判定定理是解题的关键.
25.(2020·吉林省初三一模)(教材呈现)如图是八年级下册数学教材第117页的部分内容.
结合图①,补全证明过程.
(应用)如图②,直线EF分别交矩形ABCD的边AD、BC于点E、F,将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=3,BC=4,则四边形ABFE的周长为
.
(拓展)如图③,直线EF分别交?ABCD的边AD、BC于点E、F,将?ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=,BC=4,∠C=45°,则EF的长为
.
【答案】【教材呈现】证明见解析;【应用】;【拓展】;
【分析】教材呈现:由“ASA”可证△AOE≌△COF,可得OE=OF,由对角线互相平分的四边形是平行四边形可证四边形AFCE是平行四边形,即可证平行四边形AFCE是菱形;
应用:过点F作FH⊥AD于H,由折叠的性质可得AF=CF,∠AFE=∠EFC,由勾股定理可求BF的长,EF的长,拓展:过点A作AN⊥BC,交CB的延长线于N,过点F作FM⊥AD于M,由等腰直角三角形的性质可求AN=BN=2,由勾股定理可求AE=AF=,再利用勾股定理可求EF的长.
【解析】解:【教材呈现】∵四边形ABCD是矩形,∴AE∥CF,∴∠EAO=∠FCO,
∵EF垂直平分AC,∴AO=CO,∠AOE=∠COF=90°,∴△AOE≌△COF(ASA)∴OE=OF,
又∵AO=CO,∴四边形AFCE是平行四边形,
∵EF⊥AC,∴平行四边形AFCE是菱形;
【应用】如图,过点F作FH⊥AD于H,
∵将矩形ABCD沿EF翻折,使点C的对称点与点A重合,∴AF=CF,∠AFE=∠EFC,
∵AF2=BF2+AB2,∴(4﹣BF)2=BF2+9,∴BF=,∴AF=CF=,
∵AD∥BC,∴∠AEF=∠EFC=∠AFE,∴AE=AF=,
∵∠B=∠BAD=∠AHF=90°,∴四边形ABFH是矩形,
∴AB=FH=3,AH=BF=,∴EH=,∴EF===,
∴四边形ABFE的周长=AB+BF+AE+EF=3+++=,故答案为:.
【拓展】如图,过点A作AN⊥BC,交CB的延长线于N,过点F作FM⊥AD于M,
∵四边形ABCD是平行四边形,∠C=45°,∴∠ABC=135°,∴∠ABN=45°,
∵AN⊥BC,∴∠ABN=∠BAN=45°,∴AN=BN=AB=2,
∵将?ABCD沿EF翻折,使点C的对称点与点A重合,∴AF=CF,∠AFE=∠EFC,
∵AD∥BC,∴∠AEF=∠EFC=∠AFE,∴AE=AF,
∵AF2=AN2+NF2,∴AF2=4+(6﹣AF)2,∴AF=,∴AE=AF=,
∵AN∥MF,AD∥BC,∴四边形ANFM是平行四边形,
∵AN⊥BC,∴四边形ANFM是矩形,∴AN=MF=2,∴AM===,
∴ME=AE﹣AM=,∴EF===,故答案为:.
【点睛】本题是四边形综合题,考查了平行四边形的性质,菱形的性质,折叠的性质,全等三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造直角三角形是本题的关键.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
