湘教版八年级下学期复习专题9菱形的性质与判定(含解析)
文档属性
| 名称 | 湘教版八年级下学期复习专题9菱形的性质与判定(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下学期复习专题9菱形的性质与判定
一、单选题
1.如图,若菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是(???
)
A.?20?????????????????????????????????????????B.?24?????????????????????????????????????????C.?40?????????????????????????????????????????D.?48
2.菱形具有而一般平行四边形不具有的性质是(
??)
A.?对边相等????????????????????B.?对角相等????????????????????C.?对角线互相垂直????????????????????D.?对角线互相平分
3.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是(??
)
A.?18???????????????????????????????????B.?18
???????????????????????????????????C.?9
???????????????????????????????????D.?6
4.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是(???
)
A.??????????????????????????????????????????B.?1?????????????????????????????????????????C.??????????????????????????????????????????D.?2
5.如图,已知菱形ABCD的对角线交于点O,DB=6,AD=5,则菱形ABCD的面积为(???
)
A.?20?????????????????????????????????????????B.?24?????????????????????????????????????????C.?30?????????????????????????????????????????D.?36
6.下列给出的条件中,能判定一个四边形是菱形的是(???
)
A.?一组对边平行且相等,有一个角是直角
B.?两组对边分别相等,并且有一条对角线平分一组内角
C.?两条对角线互相平分,并且有一组邻角相等
D.?一组对边平行,一组对边相等,并且对角线互相垂直
7.如图,四边形
是平行四边形,要使它变成菱形,需要添加的条件是(
??)
A.?AC=BD??????????????????????????????B.?AD=BC??????????????????????????????C.?AB=BC??????????????????????????????D.?AB=CD
8.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
A.?四边形ABCD是梯形???????????????B.?四边形ABCD是菱形?????????????C.?对角线AC=BD?????????????D.?AD=BC
9.在四边形ABCD中,对角线AC、BD相交于点O,给出下列条件:①AB∥CD;
②AB=CD;
③OA=OC;④OB=OD;
⑤AC⊥BD;⑥AC平分∠BAD.则下列各组组合中,不能推出四边形ABCD为菱形的是(??
)
A.?①②④????????????????????????????????B.?③④⑤????????????????????????????????C.?①②⑤????????????????????????????????D.?①②⑥
10.一个菱形的周长为8cm,高为1cm,这个菱形两邻角度数之比为( )
A.?3:1?????????????????????????????????????????B.?4:1?????????????????????????????????C.?5:1????????????????????????????????D.?6:1
二、填空题
11.已知菱形两条对角线的长分别为5cm和12cm,则这个菱形的面积是cm2________.
12.菱形的面积为24,一条对角线长为6,则它的周长是________.
13.如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF=________°.
14.如图,ABCD是对角线互相垂直的四边形,且0B=OD,请你添加一个适当的条件:
________使ABCD成为菱形.(只需添加一个即可)
15.如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是________.
三、解答题
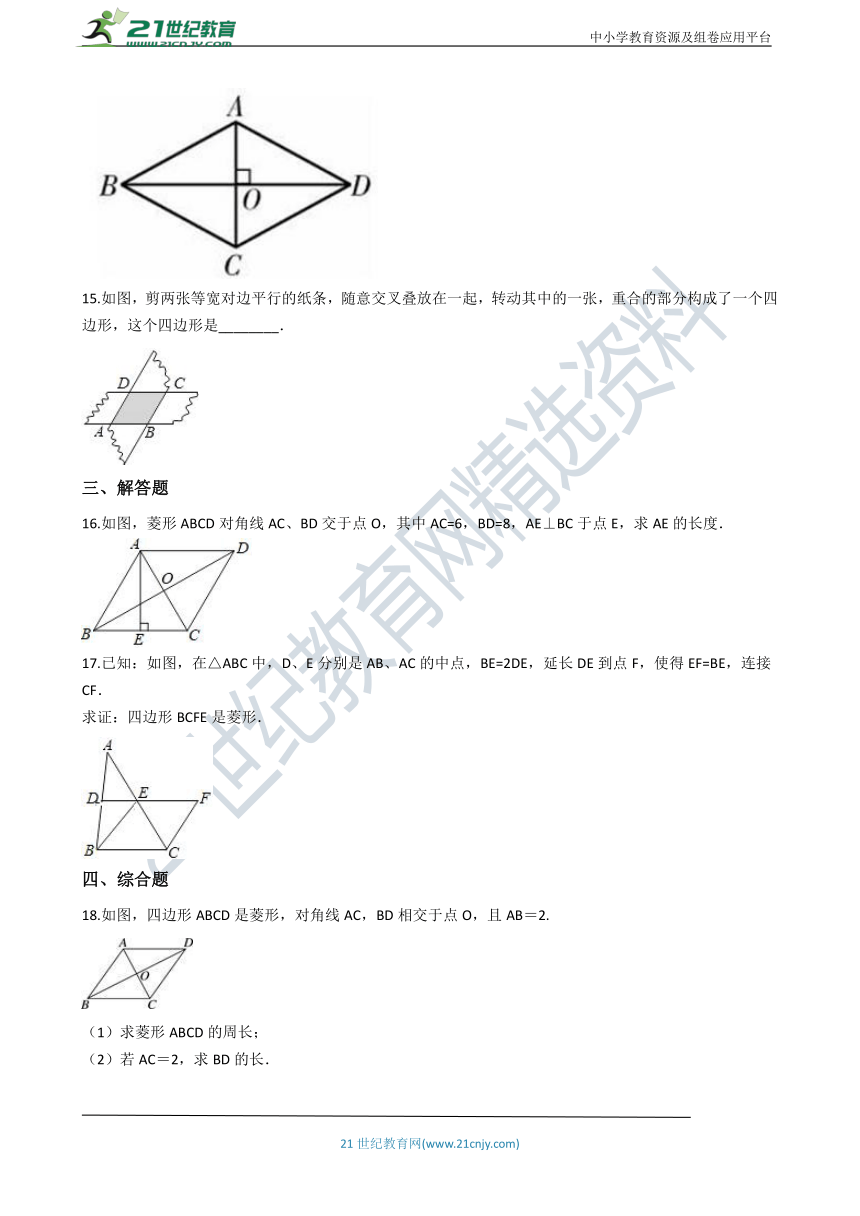
16.如图,菱形ABCD对角线AC、BD交于点O,其中AC=6,BD=8,AE⊥BC于点E,求AE的长度.
17.已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
求证:四边形BCFE是菱形.
四、综合题
18.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=2.
(1)求菱形ABCD的周长;
(2)若AC=2,求BD的长.
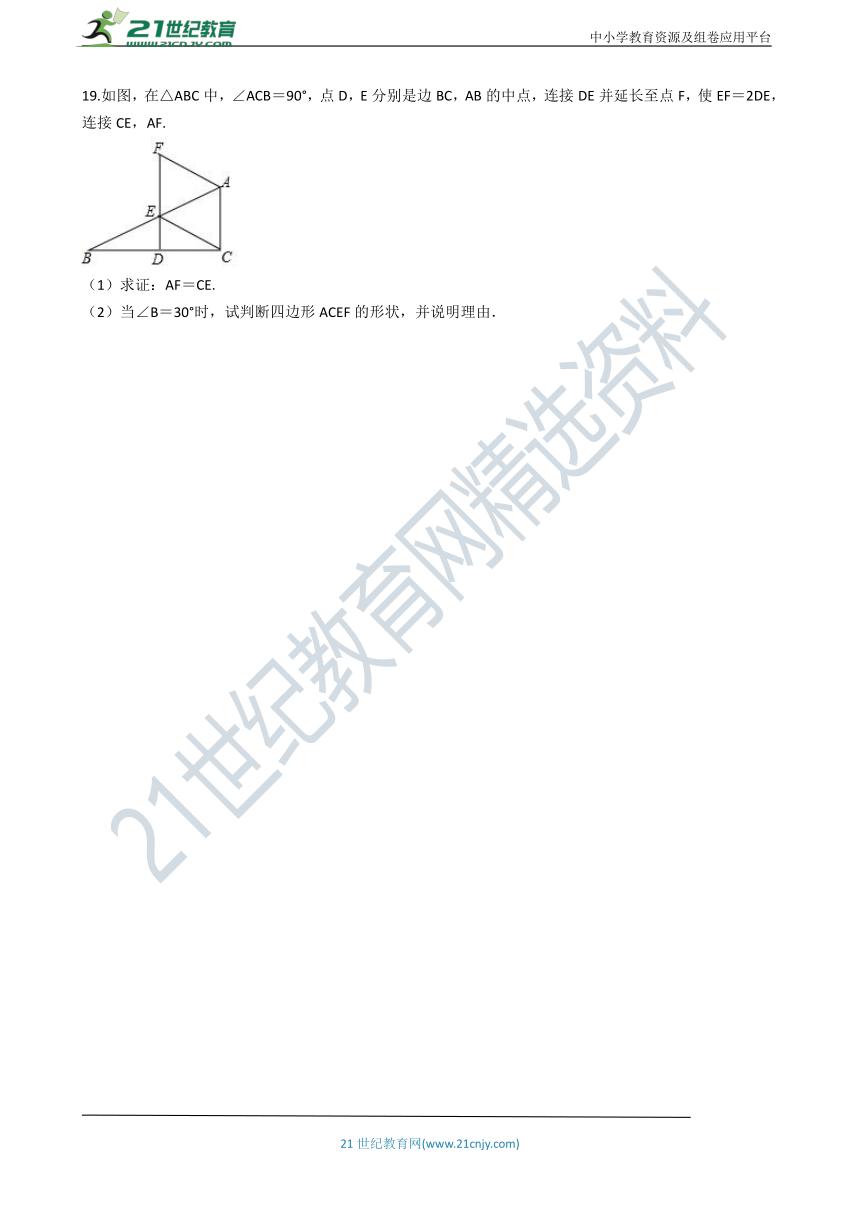
19.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB的中点,连接DE并延长至点F,使EF=2DE,连接CE,AF.
(1)求证:AF=CE.
(2)当∠B=30°时,试判断四边形ACEF的形状,并说明理由.
答案解析部分
一、单选题
1.【答案】
A
解:∵四边形ABCD中菱形,
∴AC⊥BD且AC与BD互相平分,
∴AB==5,
∵AB=BC=CD=DA,
∴菱形ABCD的周长是4×5=20.
故答案为:A
2.【答案】
C
解:∵菱形具有的性质是:对边相等,对角相等,对角线互相垂直且平分;平行四边形具有的性质是:对边相等,对角相等,对角线互相平分;
∴菱形具有而一般平行四边形不具有的性质是:对角线互相垂直.
故答案为:C.
3.【答案】
D
解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∵四边形ABCD是菱形,
∴BD⊥AC于O,AO=
AC=
×6=3,
Rt△AOB中,∠OAB=30°,
∴OB=
,
∴BD=2OB=2
,
∴菱形ABCD的面积=
=
=6
,
故答案为:D
4.【答案】
B
解:做点N关于AC的对称点,连接MN,与AC相交于一点,当点P位于此位置时,MP+PN是最小的,
即MN=AD,
所以MP+PN=1.
故答案为:B
5.【答案】
B
解:∵OD=
BD=3,
∴AO=
=4
∴AC=8,
故可得菱形ABCD的面积为
×8×6=24.
故答案为:B.
6.【答案】
B
解:A选项一组对边平行且相等,可以判断这是个平行四边形,有一个角是直角的平行四边形可以判定是矩形,所以不对;
B选项两组对边分别相等,可以判断这是个平行四边形,有一条对角线平分一组内角的平行四边形可以判定是菱形,所以正确;
C选项两条对角线互相平分,可以判断这是个平行四边形,一组邻角相等可以判断这两个角都是直角,可以判定是矩形,所以不对;
D选项一组对边平行,一组对边相等,不能判断是个平行四边形,即使有对角线互相垂直也不能判定是菱形,所以不对。
故答案为:B
7.【答案】
C
解:A.添加AC=BD可证明平行四边形ABCD是矩形,不能使它变成菱形,故此选项错误;
B.添加AD=BC不能证明平行四边形ABCD是菱形,故此选项错误;
C.添加AB=BC可证明平行四边形ABCD是菱形,故此选项正确;
D.添加AB=CD不能可证明平行四边形ABCD是变成菱形,故此选项错误;
故答案为:C.
8.【答案】
D
解:∵在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,
∴EF∥AD,HG∥AD,
∴EF∥HG;
同理,HE∥GF,
∴四边形EFGH是平行四边形;
A、若四边形ABCD是梯形时,AD≠CD,则GH≠FE,这与平行四边形EFGH的对边GH=FE相矛盾;故本选项错误;
B、若四边形ABCD是菱形时,点EFGH四点共线;故本选项错误;
C、若对角线AC=BD时,四边形ABCD可能是等腰梯形,证明同A选项;故本选项错误;
D、当AD=BC时,GH=GF;所以平行四边形EFGH是菱形;故本选项正确;
故选:D.
9.【答案】
A
解:∵AB=CD;AB∥CD,
∴四边形ABCD是平行四边形,
如果加上条件⑤AC⊥BD可利用对角线互相垂直的平行四边形是菱形进行判定;故C不符合题意,
如果加上条件⑥AC平分∠BAD可证明邻边相等,根据邻边相等的平行四边形是菱形进行判定;故D不符合题意,
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
如果加上条件⑤,根据对角线垂直的平行四边形是菱形进行判定;故B不符合题意,
故选:A.
10.【答案】
C
解:如图:∵菱形的周长是8cm,
∴AD=2cm,
∵高是1cm,
∴DE=1m,
∴在Rt△DAE中,sin∠A==
,
∴∠A=30°,
∴∠B=180°﹣∠A=150°,
∴这个菱形两邻角的度数比为5:1.
故选:C.
二、填空题
11.【答案】
30
解:菱形的面积=
×5×12=30(cm2).
故答案为:30.
12.【答案】
20
解:如下图所示:
∵S菱形=·AC·BD=24,令AC=6,
∴BD=8,
∴BO=4,AO=3,
在Rt△ABO中,AB2=AO2+BO2
,
即AB2=32+42
,
∴AB=5,
∴菱形的周长=5×4=20.
故答案为:20.
13.【答案】
75
解:如下图,连接BD,BF,
∵∠BAD=70°,
∴∠ADC=110°
,
又∵EF垂直平分AB,AC垂直平分BD,
∴AF=BF,BF=DF,
∴AF=DF,
∴∠FAD=∠FDA=35°,
∴∠CDF=110°-35°=75°.
故答案为:75°.
14.【答案】
答案不唯一,如
或
或
或
等
解:添加:OA=OC,
理由:∵OA=OC,OB=OC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
故答案为:OB=OD(答案不唯一)
15.【答案】
菱形
解:过点D分别作AB,BC边上的高为AE,AF,
∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);
∵DE⊥AB,DF⊥BC,
∴DE=DF(两纸条相同,纸条宽度相同),
∵S平行四边形ABCD=AB?ED=BC?DF,
∴AB=CB,
∴四边形ABCD是菱形,
故答案为:菱形.
三、解答题
16.【答案】
解:∵四边形ABCD是菱形,
∴CO=
AC=3,BO=
BD=4,AO⊥BO,
∴BC=
=5,
∴S菱形ABCD=
AC?BD=
×6×8=24,
∵S菱形ABCD=BC×AE,
∴BC×AE=24,
∴AE=
17.【答案】
证明:∵BE=2DE,EF=BE,
∴EF=2DE.
∵D、E分别是AB、AC的中点,
∴BC=2DE且DE∥BC.
∴EF=BC.
又EF∥BC,
∴四边形BCFE是平行四边形.
又EF=BE,
∴四边形BCFE是菱形
四、综合题
18.【答案】
(1)∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∵AB=2,
∴菱形ABCD的周长=4×2=8
(2)解:
∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO
∵AC=2,
∴AO=CO=1
∵BO=
,
∴BD=2BO=
19.【答案】
(1)证明:∵点D、E分别是边BC、AB的中点,∴DE∥AC且AC=2DE,
∵EF=2DE,∴EF=AC
∴四边形ACEF是平行四边形
∴AF=CE
(2)解:四边形ACEF是菱形。理由是:
∵∠ACB=90°,点E是AB的中点,
∴CE=AE,
∵∠B=30°,∠ACB=90°,
∴AC=AE,
∴AC=CE,
∴四边形ACEF是菱形.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下学期复习专题9菱形的性质与判定
一、单选题
1.如图,若菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是(???
)
A.?20?????????????????????????????????????????B.?24?????????????????????????????????????????C.?40?????????????????????????????????????????D.?48
2.菱形具有而一般平行四边形不具有的性质是(
??)
A.?对边相等????????????????????B.?对角相等????????????????????C.?对角线互相垂直????????????????????D.?对角线互相平分
3.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是(??
)
A.?18???????????????????????????????????B.?18
???????????????????????????????????C.?9
???????????????????????????????????D.?6
4.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是(???
)
A.??????????????????????????????????????????B.?1?????????????????????????????????????????C.??????????????????????????????????????????D.?2
5.如图,已知菱形ABCD的对角线交于点O,DB=6,AD=5,则菱形ABCD的面积为(???
)
A.?20?????????????????????????????????????????B.?24?????????????????????????????????????????C.?30?????????????????????????????????????????D.?36
6.下列给出的条件中,能判定一个四边形是菱形的是(???
)
A.?一组对边平行且相等,有一个角是直角
B.?两组对边分别相等,并且有一条对角线平分一组内角
C.?两条对角线互相平分,并且有一组邻角相等
D.?一组对边平行,一组对边相等,并且对角线互相垂直
7.如图,四边形
是平行四边形,要使它变成菱形,需要添加的条件是(
??)
A.?AC=BD??????????????????????????????B.?AD=BC??????????????????????????????C.?AB=BC??????????????????????????????D.?AB=CD
8.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
A.?四边形ABCD是梯形???????????????B.?四边形ABCD是菱形?????????????C.?对角线AC=BD?????????????D.?AD=BC
9.在四边形ABCD中,对角线AC、BD相交于点O,给出下列条件:①AB∥CD;
②AB=CD;
③OA=OC;④OB=OD;
⑤AC⊥BD;⑥AC平分∠BAD.则下列各组组合中,不能推出四边形ABCD为菱形的是(??
)
A.?①②④????????????????????????????????B.?③④⑤????????????????????????????????C.?①②⑤????????????????????????????????D.?①②⑥
10.一个菱形的周长为8cm,高为1cm,这个菱形两邻角度数之比为( )
A.?3:1?????????????????????????????????????????B.?4:1?????????????????????????????????C.?5:1????????????????????????????????D.?6:1
二、填空题
11.已知菱形两条对角线的长分别为5cm和12cm,则这个菱形的面积是cm2________.
12.菱形的面积为24,一条对角线长为6,则它的周长是________.
13.如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF=________°.
14.如图,ABCD是对角线互相垂直的四边形,且0B=OD,请你添加一个适当的条件:
________使ABCD成为菱形.(只需添加一个即可)
15.如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是________.
三、解答题
16.如图,菱形ABCD对角线AC、BD交于点O,其中AC=6,BD=8,AE⊥BC于点E,求AE的长度.
17.已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
求证:四边形BCFE是菱形.
四、综合题
18.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=2.
(1)求菱形ABCD的周长;
(2)若AC=2,求BD的长.
19.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB的中点,连接DE并延长至点F,使EF=2DE,连接CE,AF.
(1)求证:AF=CE.
(2)当∠B=30°时,试判断四边形ACEF的形状,并说明理由.
答案解析部分
一、单选题
1.【答案】
A
解:∵四边形ABCD中菱形,
∴AC⊥BD且AC与BD互相平分,
∴AB==5,
∵AB=BC=CD=DA,
∴菱形ABCD的周长是4×5=20.
故答案为:A
2.【答案】
C
解:∵菱形具有的性质是:对边相等,对角相等,对角线互相垂直且平分;平行四边形具有的性质是:对边相等,对角相等,对角线互相平分;
∴菱形具有而一般平行四边形不具有的性质是:对角线互相垂直.
故答案为:C.
3.【答案】
D
解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∵四边形ABCD是菱形,
∴BD⊥AC于O,AO=
AC=
×6=3,
Rt△AOB中,∠OAB=30°,
∴OB=
,
∴BD=2OB=2
,
∴菱形ABCD的面积=
=
=6
,
故答案为:D
4.【答案】
B
解:做点N关于AC的对称点,连接MN,与AC相交于一点,当点P位于此位置时,MP+PN是最小的,
即MN=AD,
所以MP+PN=1.
故答案为:B
5.【答案】
B
解:∵OD=
BD=3,
∴AO=
=4
∴AC=8,
故可得菱形ABCD的面积为
×8×6=24.
故答案为:B.
6.【答案】
B
解:A选项一组对边平行且相等,可以判断这是个平行四边形,有一个角是直角的平行四边形可以判定是矩形,所以不对;
B选项两组对边分别相等,可以判断这是个平行四边形,有一条对角线平分一组内角的平行四边形可以判定是菱形,所以正确;
C选项两条对角线互相平分,可以判断这是个平行四边形,一组邻角相等可以判断这两个角都是直角,可以判定是矩形,所以不对;
D选项一组对边平行,一组对边相等,不能判断是个平行四边形,即使有对角线互相垂直也不能判定是菱形,所以不对。
故答案为:B
7.【答案】
C
解:A.添加AC=BD可证明平行四边形ABCD是矩形,不能使它变成菱形,故此选项错误;
B.添加AD=BC不能证明平行四边形ABCD是菱形,故此选项错误;
C.添加AB=BC可证明平行四边形ABCD是菱形,故此选项正确;
D.添加AB=CD不能可证明平行四边形ABCD是变成菱形,故此选项错误;
故答案为:C.
8.【答案】
D
解:∵在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,
∴EF∥AD,HG∥AD,
∴EF∥HG;
同理,HE∥GF,
∴四边形EFGH是平行四边形;
A、若四边形ABCD是梯形时,AD≠CD,则GH≠FE,这与平行四边形EFGH的对边GH=FE相矛盾;故本选项错误;
B、若四边形ABCD是菱形时,点EFGH四点共线;故本选项错误;
C、若对角线AC=BD时,四边形ABCD可能是等腰梯形,证明同A选项;故本选项错误;
D、当AD=BC时,GH=GF;所以平行四边形EFGH是菱形;故本选项正确;
故选:D.
9.【答案】
A
解:∵AB=CD;AB∥CD,
∴四边形ABCD是平行四边形,
如果加上条件⑤AC⊥BD可利用对角线互相垂直的平行四边形是菱形进行判定;故C不符合题意,
如果加上条件⑥AC平分∠BAD可证明邻边相等,根据邻边相等的平行四边形是菱形进行判定;故D不符合题意,
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
如果加上条件⑤,根据对角线垂直的平行四边形是菱形进行判定;故B不符合题意,
故选:A.
10.【答案】
C
解:如图:∵菱形的周长是8cm,
∴AD=2cm,
∵高是1cm,
∴DE=1m,
∴在Rt△DAE中,sin∠A==
,
∴∠A=30°,
∴∠B=180°﹣∠A=150°,
∴这个菱形两邻角的度数比为5:1.
故选:C.
二、填空题
11.【答案】
30
解:菱形的面积=
×5×12=30(cm2).
故答案为:30.
12.【答案】
20
解:如下图所示:
∵S菱形=·AC·BD=24,令AC=6,
∴BD=8,
∴BO=4,AO=3,
在Rt△ABO中,AB2=AO2+BO2
,
即AB2=32+42
,
∴AB=5,
∴菱形的周长=5×4=20.
故答案为:20.
13.【答案】
75
解:如下图,连接BD,BF,
∵∠BAD=70°,
∴∠ADC=110°
,
又∵EF垂直平分AB,AC垂直平分BD,
∴AF=BF,BF=DF,
∴AF=DF,
∴∠FAD=∠FDA=35°,
∴∠CDF=110°-35°=75°.
故答案为:75°.
14.【答案】
答案不唯一,如
或
或
或
等
解:添加:OA=OC,
理由:∵OA=OC,OB=OC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
故答案为:OB=OD(答案不唯一)
15.【答案】
菱形
解:过点D分别作AB,BC边上的高为AE,AF,
∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);
∵DE⊥AB,DF⊥BC,
∴DE=DF(两纸条相同,纸条宽度相同),
∵S平行四边形ABCD=AB?ED=BC?DF,
∴AB=CB,
∴四边形ABCD是菱形,
故答案为:菱形.
三、解答题
16.【答案】
解:∵四边形ABCD是菱形,
∴CO=
AC=3,BO=
BD=4,AO⊥BO,
∴BC=
=5,
∴S菱形ABCD=
AC?BD=
×6×8=24,
∵S菱形ABCD=BC×AE,
∴BC×AE=24,
∴AE=
17.【答案】
证明:∵BE=2DE,EF=BE,
∴EF=2DE.
∵D、E分别是AB、AC的中点,
∴BC=2DE且DE∥BC.
∴EF=BC.
又EF∥BC,
∴四边形BCFE是平行四边形.
又EF=BE,
∴四边形BCFE是菱形
四、综合题
18.【答案】
(1)∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∵AB=2,
∴菱形ABCD的周长=4×2=8
(2)解:
∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO
∵AC=2,
∴AO=CO=1
∵BO=
,
∴BD=2BO=
19.【答案】
(1)证明:∵点D、E分别是边BC、AB的中点,∴DE∥AC且AC=2DE,
∵EF=2DE,∴EF=AC
∴四边形ACEF是平行四边形
∴AF=CE
(2)解:四边形ACEF是菱形。理由是:
∵∠ACB=90°,点E是AB的中点,
∴CE=AE,
∵∠B=30°,∠ACB=90°,
∴AC=AE,
∴AC=CE,
∴四边形ACEF是菱形.
21世纪教育网(www.21cnjy.com)
同课章节目录
