专题3一次函数—3.3一次函数应用题3其它问题-2021届鲁教版(五四制)九年级数学专题复习训练(word版含解析)
文档属性
| 名称 | 专题3一次函数—3.3一次函数应用题3其它问题-2021届鲁教版(五四制)九年级数学专题复习训练(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 634.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 07:24:04 | ||
图片预览



文档简介
一次函数应用题-其它费用
【经典例题1】某市电力公司采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.55元计算费用,每月用电超过100度时,超过部分按每度0.60元计算.
(1)设每月用电x度时,应交电费y元,写出y与x之间的函数关系式,并写出自变量的取值范围;
(2)小王家一月份用了115度电,应交电费多少元?
(3)小王家三月份交纳电费49.5元,求小王家三月份用了多少度电?
练习1-1为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量/t 单价/(元/t)
不大于10t部分 1.5
大于10t且不大于mt部分20≤m≤50 2
大于mt部分 3
(1)若某用户六月份用水量为18t,求其应缴纳的水费;
(2)记该用户六月份用水量为xt,缴纳水费y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40t,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
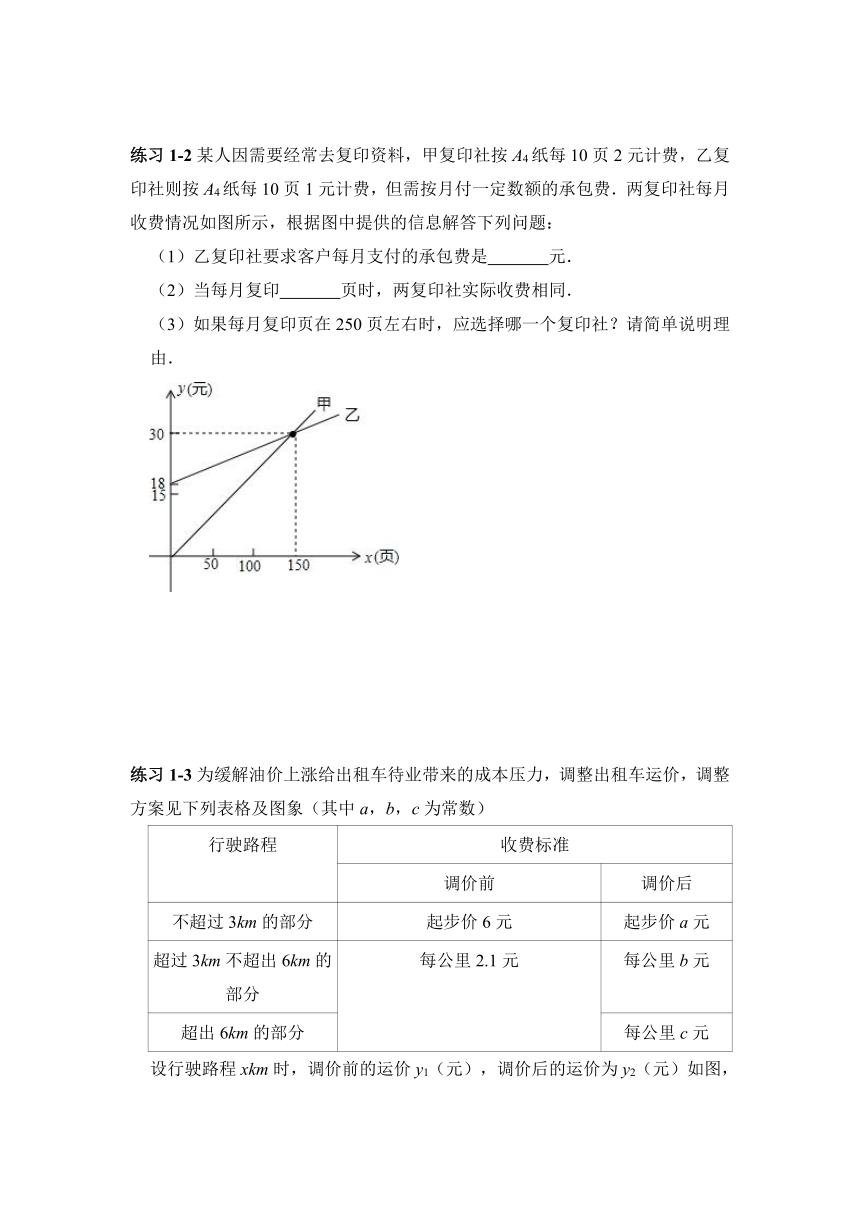
练习1-2某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页1元计费,但需按月付一定数额的承包费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的承包费是 元.
(2)当每月复印 页时,两复印社实际收费相同.
(3)如果每月复印页在250页左右时,应选择哪一个复印社?请简单说明理由.
练习1-3为缓解油价上涨给出租车待业带来的成本压力,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 收费标准
调价前 调价后
不超过3km的部分 起步价6元 起步价a元
超过3km不超出6km的部分 每公里2.1元 每公里b元
超出6km的部分
每公里c元
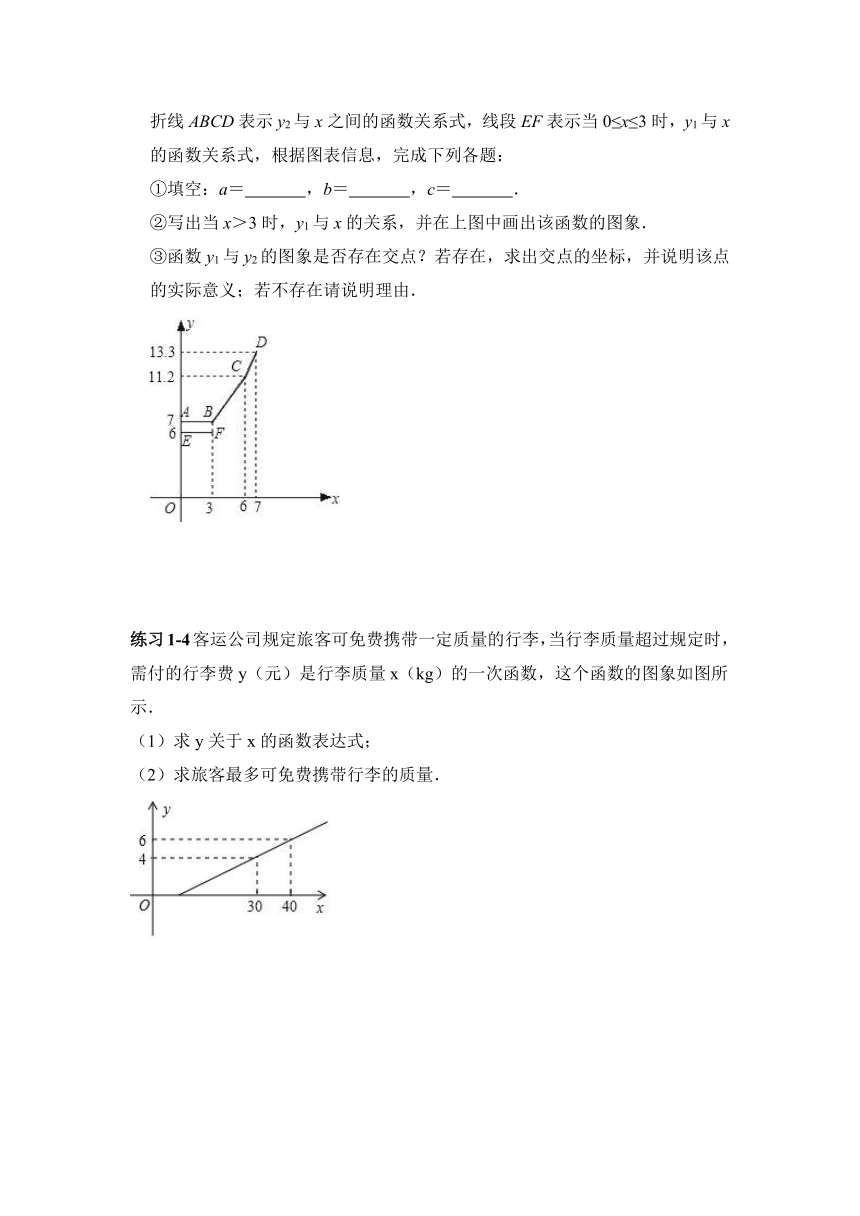
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
①填空:a= ,b= ,c= .
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.
练习1-4客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,这个函数的图象如图所示.
(1)求y关于x的函数表达式;
(2)求旅客最多可免费携带行李的质量.
时间优化问题
【经典例题2】小碚向某校食堂王经理建议食堂就餐情况,经调查发现就餐时,有520人排队吃饭就餐,就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加,食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12人,每个打饭窗口1每分钟打饭菜10人.已知食堂的前a分钟只开放了两个打饭窗口;某一天食堂排队等候的学生数y(人)与打饭菜时间x(分钟)的关系如图所示.
(1)求a的值;
(2)求排队到第16分钟时,食堂排队等候打饭菜的学生人数;
(3)若要在开始打饭菜后8分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃,那么小碚应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口?
练习2-1为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时?
练习2-2如图1是一个由两个圆柱形构成的容器,最下面的圆柱形底面半径R1=8m.匀速地向空容器内注水,水面高度h(单位:米)与时间t(单位:小时)的关系如图2所示.
(1)求水面高度h与时间t的函数关系式;
(2)求注水的速度(单位:立方米每小时),并求容器内水的体积V与注水时间t的函数关系式;
(3)求上面圆柱的底面半径(壁厚忽略不计).
练习2-3一个容积为200升的水箱,安装有A、B两个水管,加水过程中A水管始终打开,B水管可随时打开或关闭,两水管匀速为水箱加水,且水流速度为定值,当水箱加满时,加水过程结束.
(1)如图是某次加水过程中水箱中水量y(升)与时间x(分)之间的函数图象.
①分别求A、B两水管的水流速度.
②求y与x的函数关系式,
(2)当水箱中无水时,13分钟将水箱加满,求A水管打开后几分钟打开B水管.
练习2-4实验室里,水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计).现三个容器中,只有甲中有水,水位高2cm,如图①所示.若每分钟同时向乙、丙容器中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.
(1)乙、丙两容器的底面积之比为 .
(2)图②中a的值为 ,b的值为 .
(3)注水多少分钟后,乙比甲的水位高2cm?
练习2-5如图所示的是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图Z12-6-2所示.
(图1) (图2)
(1)若乙槽底面积为48平方厘米(壁厚不计),则乙槽中铁块的体积是__cm3;
(2)若乙槽中铁块的体积为98 cm3(壁厚不计),则甲槽底面积是____cm2.
其它问题
【经典例题3】根据国家颁布的“养老保险执行标准”绘制出我市行政事业人员的养老保险个人月缴费y(元)随个人月工资x(元)变化的图象如图~所示,请你根据图象解答下面的问题:
(1)教数学的张老师是中学一级教师,月工资是1568元,张老师每月应缴纳养老保险多少元?
(2)教英语的陈老师是位高级教师,他每月要缴纳养老保险140.21元,求陈老师的每月工资是多少元?
练习3-1(2020?陕西)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式;
(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?
练习3-2已知贺兰山山区的平均气温与该山区的海拔高度的关系见下表:
海拔高度(米) 0 100 200 300 400 500 …
平均气温(℃) 22 21.5 21 20.5 20 19.5 …
(1)平均气温y(℃)是海拔高度x(米)的什么函数?写出y与x之间的函数关系式.
(2)若某种植物适宜生长在18℃~20℃(包括18℃,也包括20℃)的山区,请问该植物适宜种植在海拔为多少米的山区?
练习3-3(2020·广东高州·)空气中传播的速度与气温之间的关系式为;当时,某人看到烟花燃放后才听到声音,则此人与燃放烟花所在地的距离为_________.
练习3-4药品研究所开发一种抗菌素新药,经过多年的动物实验之后,首次用于临床人体试验,测得成人服药后血液中药物浓度(微克/毫升)与服药后时间(时)之间的函数关系如图所示,下列说法正确的是( )
A.当,随增大而减小
B.当,随增大而增大
C.若点和点都在函数图象上,则
D.若血液中药物浓度达到6微克/毫升及以上浓度为有效治疗,则当为有效治疗时间
一次函数应用题-其它费用
【经典例题1】某市电力公司采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.55元计算费用,每月用电超过100度时,超过部分按每度0.60元计算.
(1)设每月用电x度时,应交电费y元,写出y与x之间的函数关系式,并写出自变量的取值范围;
(2)小王家一月份用了115度电,应交电费多少元?
(3)小王家三月份交纳电费49.5元,求小王家三月份用了多少度电?
【解】:(1)由题意可得,
当0<x≤100时,y=0.55x,
当x>100时,y=0.55×100+(x﹣100)×0.6=0.6x﹣5,
由上可得,y与x之间的函数关系式是y=;
(2)当x=115时,y=0.6×115﹣5=64(元),
答:小王家一月份用了115度电,应交电费64元;
(3)∵100×0.55=55>49.5,
∴小王家三月份用电在100度以内,
当y=49.5时,49.5=0.55x,
解得,x=90,
答:小王家三月份用了90度电.
练习1-1为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量/t 单价/(元/t)
不大于10t部分 1.5
大于10t且不大于mt部分20≤m≤50 2
大于mt部分 3
(1)若某用户六月份用水量为18t,求其应缴纳的水费;
(2)记该用户六月份用水量为xt,缴纳水费y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40t,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
【解析】(1)六月份应缴纳的水费为:1.5×10+2×8=31(元);
(2)当0≤x≤10时,y=1.5x,
当10<x≤m时,y=10×1.5+2(x﹣10)=2x﹣5,
当x>m时,y=15+2(m﹣10)+3(x﹣m)=3x﹣m﹣5;
(3)①若所付费用在第2个阶段,40≤m且20≤m≤50,即40≤m≤50时,y=2×40﹣5=75元,满足条件,
②若所付费用到了第3个阶段,y=3×40﹣m﹣5=115﹣m,则70≤115﹣m≤90,
解得:25≤m≤45,
结合①可得25≤m≤45,
综上得,25≤m≤50.
练习1-2某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页1元计费,但需按月付一定数额的承包费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的承包费是 元.
(2)当每月复印 页时,两复印社实际收费相同.
(3)如果每月复印页在250页左右时,应选择哪一个复印社?请简单说明理由.
【解析】(1)由图可知,x=0时,y=18,
所以,乙复印社要求客户每月支付的承包费是18元;
(2)∵两函数图象的交点为(150,30),
∴当每月复印150页时,两复印社实际收费相同;
(3)选择乙.
理由是:当复印页少于150页时,甲的收费较低,
当复印页等于150页时,两复印社收费相同,
当复印页超过150页时,乙的收费较低,
∵250>150,
∴当复印页超过150页时,乙的收费较低.
故答案为:(1)18,(2)150.
练习1-3为缓解油价上涨给出租车待业带来的成本压力,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 收费标准
调价前 调价后
不超过3km的部分 起步价6元 起步价a元
超过3km不超出6km的部分 每公里2.1元 每公里b元
超出6km的部分
每公里c元
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
①填空:a= ,b= ,c= .
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.
【解析】①由图可知,a=7元,
b=(11.2﹣7)÷(6﹣3)=1.4元,
c=(13.3﹣11.2)÷(7﹣6)=2.1元;
②由图得,当x>3时,y1与x的关系式是:
y1=6+(x﹣3)×2.1,
整理得,y1=2.1x﹣0.3;
③由图得,当3<x<6时,y2与x的关系式是:
y2=7+(x﹣3)×1.4,
整理得,y2=1.4x+2.8;
所以,当y1=y2时,交点存在,
即,2.1x﹣0.3=1.4x+2.8,
解得,x=,y=9;
所以,函数y1与y2的图象存在交点(,9);
其意义为:当x<时,是方案调价前合算,当x>时,方案调价后合算;
练习1-4客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,这个函数的图象如图所示.
(1)求y关于x的函数表达式;
(2)求旅客最多可免费携带行李的质量.
【答案】(1)(2)
【解析】
(1)根据(30,4)、(40,6)利用待定系数法,即可求出当行李的质量x超过规定时,y与x之间的函数表达式;
(2)令y=0,求出x值,此题得解.
解:(1)设y与x的函数表达式为y=kx+b,
由题意可得:
解得:
∴(x>10);
(2)当y=0,,
∴x=10,
∴旅客最多可免费携带行李的质量为10kg.
【点睛】
本题主要考查求一次函数解析式,熟练掌握利用待定系数法求解函数表达式是解题的关键.
时间优化问题
【经典例题2】小碚向某校食堂王经理建议食堂就餐情况,经调查发现就餐时,有520人排队吃饭就餐,就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加,食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12人,每个打饭窗口1每分钟打饭菜10人.已知食堂的前a分钟只开放了两个打饭窗口;某一天食堂排队等候的学生数y(人)与打饭菜时间x(分钟)的关系如图所示.
(1)求a的值;
(2)求排队到第16分钟时,食堂排队等候打饭菜的学生人数;
(3)若要在开始打饭菜后8分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃,那么小碚应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口?
【解析】(1)由图象知,520+12a﹣2×10a=424,
∴a=12;
(2)设当12≤x≤20时,y与x之间的函数关系式为y=kx+b,
由题意,得,
解得:,
∴y=﹣53x+1060,
当x=16时,y=212,
即排队到第16分钟时,食堂排队等候打饭菜的学生有212人.
(3)设需同时开放n个打饭窗口,
由题意知10n×8≥520+12×8
解得:n≥7.7,
∵n为整数,
∴n最小=8.
答:至少需要同时开放8个打饭窗口.
练习2-1为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时?
【解析】(1)设y与t的函数解析式为y=kt+b,
,
解得,,
即y与t的函数关系式是y=140t+100,
同时打开甲、乙两个进水口的注水速度是:(380﹣100)÷2=140(m3/h);
(2)∵单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.
∴甲进水口进水的速度是乙进水口进水速度的,
∵同时打开甲、乙两个进水口的注水速度是140m3/h,
∴甲进水口的进水速度为:140÷(+1)×=60(m3/h),
480÷60=8(h),
即单独打开甲进水口注满游泳池需8h.
练习2-2如图1是一个由两个圆柱形构成的容器,最下面的圆柱形底面半径R1=8m.匀速地向空容器内注水,水面高度h(单位:米)与时间t(单位:小时)的关系如图2所示.
(1)求水面高度h与时间t的函数关系式;
(2)求注水的速度(单位:立方米每小时),并求容器内水的体积V与注水时间t的函数关系式;
(3)求上面圆柱的底面半径(壁厚忽略不计).
【解析】(1)当0≤t≤1时,设水面高度h与时间t的函数关系式:h=kt,且过(1,1)
∴1=k
∴当0≤t≤1时,设水面高度h与时间t的函数关系式:h=t
当1<t≤2时,设水面高度h与时间t的函数关系式:h=mt+n,且过(1,1),(2,5)
∴
解得:
∴当1<t≤2时,设水面高度h与时间t的函数关系式:h=4t﹣3
(2)由图2可知,注满下面圆柱所花的时间是1小时,下面圆柱的高度是1米,
设注水的速度为x立方米/每小时,
∴π×82×1=1×x
∴x=64π
∴注水的速度为64π立方米/每小时,
∴容器内水的体积V与注水时间t的函数关系式:V=64πt
(3)设上面圆柱的底面半径为ym
∵π×y2×(5﹣1)=64π×1
∴y=4
∴上面圆柱的底面半径为4m
练习2-3一个容积为200升的水箱,安装有A、B两个水管,加水过程中A水管始终打开,B水管可随时打开或关闭,两水管匀速为水箱加水,且水流速度为定值,当水箱加满时,加水过程结束.
(1)如图是某次加水过程中水箱中水量y(升)与时间x(分)之间的函数图象.
①分别求A、B两水管的水流速度.
②求y与x的函数关系式,
(2)当水箱中无水时,13分钟将水箱加满,求A水管打开后几分钟打开B水管.
【解析】(1)①A水管的水流速度为:40÷8=5(升/分),
B水管的水流速度为:(200﹣40﹣8×5)÷(16﹣8)=160÷8=15(升/分);
②根据题意得
当0≤x≤8时,y=5x;
当8<x≤16时,y=40+20(x﹣8)=20x﹣120.
(2)设先打开A水管a分钟后再打开B水管,
两水管共13分钟将水箱加满,
∴5a+(5+15)(13﹣a)=200,
解得a=4.
即A水管打开4几分钟打开B水管,共13分钟将水箱加满.
练习2-4实验室里,水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计).现三个容器中,只有甲中有水,水位高2cm,如图①所示.若每分钟同时向乙、丙容器中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.
(1)乙、丙两容器的底面积之比为 .
(2)图②中a的值为 ,b的值为 .
(3)注水多少分钟后,乙比甲的水位高2cm?
【解析】(1)观察图象可知:乙、丙两容器的底面积之比为3:1.
故答案为3:1.
(2)∵乙、丙两容器的底面积之比为3:1,丙容器注入2分钟到达6cm,
∴乙容器的水位达到6cm所需时间为:2+2=4(min),
b=(10﹣2+10×3+10)÷6=8(min).
故答案为:4;8.
(3)①当2≤x≤4时,设乙容器水位高度h与时间t的函数关系式为h=kt+b(k≠0),
∵图象经过(2,2)、(4,6)两点,
∴,解得,
∴h=2t﹣2(2≤x≤4).
当h=4时,则2t﹣2=4,解得t=3;
②设t分钟后,甲容器水位为4cm,根据题意得
2+6(t﹣4)=4,
解得.
答:注水3分钟或分钟后,乙比甲的水位高2cm.
练习2-5如图所示的是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图Z12-6-2所示.
(图1) (图2)
(1)若乙槽底面积为48平方厘米(壁厚不计),则乙槽中铁块的体积是__cm3;
(2)若乙槽中铁块的体积为98 cm3(壁厚不计),则甲槽底面积是____cm2.
【解析】(1)由图象知:当水槽中没有没过铁块时4分钟水面上升了12cm,
即1分钟上升3cm,当水面没过铁块时,2分钟上升了5cm,
即1分钟上升2.5cm,
设铁块的底面积为a cm2,则乙水槽中没有没过铁块时每分钟进入水体积分别为:2.5×48cm3,没过铁块时每分钟进入水体积为3×(48-a)cm3,
∴1×3×(48-a)=1×2.5×48,解得a=8,
∴铁块的体积为:8×14=112(cm3);
(2)∵铁块的底面积为98÷14=7(cm2),设乙水槽底面积为b,根据乙水槽中没有没过铁块时每分钟进入水体积与没过铁块时每分钟进入水体积相等,得为1×3×(b-7)=1×2.5×b,解得b=42,
乙水槽每分钟进水105cm3,甲水槽每分钟降低2cm,甲水槽底面积为105÷2=52.5 cm2.
其它问题
【经典例题3】根据国家颁布的“养老保险执行标准”绘制出我市行政事业人员的养老保险个人月缴费y(元)随个人月工资x(元)变化的图象如图~所示,请你根据图象解答下面的问题:
(1)教数学的张老师是中学一级教师,月工资是1568元,张老师每月应缴纳养老保险多少元?
(2)教英语的陈老师是位高级教师,他每月要缴纳养老保险140.21元,求陈老师的每月工资是多少元?
【解析】(1)由题意,设y=kx+b(x≥557).
∵(557,38.99),(1986,139.02)在此函数的图象上,
∴,
解得.
∴y=0.07x.
当x=1568时,y=0.07×1568=109.76.
故张老师每月应缴纳养老保险109.76元;
(2)∵y=0.07x,
∴当y=140.21时,0.07x=140.21,
解得x=2003.
故陈老师的每月工资是2003元.
练习3-1(2020?陕西)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式;
(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?
【解析】(1)当0≤x≤15时,设y=kx(k≠0),
则:20=15k,
解得k,
∴y;
当15<x≤60时,设y=k′x+b(k≠0),
则:,
解得,
∴y,
∴;
(2)当y=80时,80,解得x=33,
33﹣15=18(天),
∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.
练习3-2已知贺兰山山区的平均气温与该山区的海拔高度的关系见下表:
海拔高度(米) 0 100 200 300 400 500 …
平均气温(℃) 22 21.5 21 20.5 20 19.5 …
(1)平均气温y(℃)是海拔高度x(米)的什么函数?写出y与x之间的函数关系式.
(2)若某种植物适宜生长在18℃~20℃(包括18℃,也包括20℃)的山区,请问该植物适宜种植在海拔为多少米的山区?
【答案】(1)一次函数,y=x+22(2)植物适宜种在海拔为400米到800米的山区
【解析】
(1)分析数据可知:高度每增加100米,温度下降0.5℃,据此得知函数为一次函数,设一次函数解析式为:,将表中的两组值代入即可得出答案;
(2)取y=18,20,分别求出高度x的值,再回答问题.
解:(1)根据数据可知高度每增加100米,温度下降0.5℃,得出为一次函数;
设此一次函数解析式为:,
将代入解析式,得
,
解得:,
y与x之间的函数关系式为:;
(2)∵中,,
所以随的增大而减小.
当时,,;
当时,,,
所以
即该植物适宜种植在海拔为400米至800米(包括400米和800米)的山区.
【点睛】
此题考查一次函数的应用,正确表示函数关系式是关键.难度不大.
练习3-3(2020·广东高州·)空气中传播的速度与气温之间的关系式为;当时,某人看到烟花燃放后才听到声音,则此人与燃放烟花所在地的距离为_________.
【答案】1721
【解析】
把气温代入函数关系式求出音速,再根据路程=速度×时间计算即可得解.
解:当x=22时,
344.2×5=1721(米).
答:此人与燃放烟花所在地距离是1721米.
故答案为:
【点睛】
本题考查了一次函数的应用.掌握读懂题目信息,已知自变量的值,求相应的函数值是解题的关键.
练习3-4药品研究所开发一种抗菌素新药,经过多年的动物实验之后,首次用于临床人体试验,测得成人服药后血液中药物浓度(微克/毫升)与服药后时间(时)之间的函数关系如图所示,下列说法正确的是( )
A.当,随增大而减小
B.当,随增大而增大
C.若点和点都在函数图象上,则
D.若血液中药物浓度达到6微克/毫升及以上浓度为有效治疗,则当为有效治疗时间
【答案】C
【解析】
结合图像可判断A,B,求出两段函数表达式,即可判断C,再求出当y≥6时的x范围可判断D.
解:A:当,随增大而增大,选项错误;
B:当时,随增大而增大,当时,随增大而减小,选项错误;
C:设当0≤x≤3时,设y=kx,
∴3k=8,解得:k=,
∴y=x,
当3<x≤14时,设y=ax+b,
∴,解得:,
∴;
∴当x=2时,;当x=5时,,,选项正确;
D:y=x中,令y=6,解得:x=,
中,令y=6,解得:x=,
∴当为有效治疗时间,选项错误.
故选:C.
【点睛】
本题主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
【经典例题1】某市电力公司采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.55元计算费用,每月用电超过100度时,超过部分按每度0.60元计算.
(1)设每月用电x度时,应交电费y元,写出y与x之间的函数关系式,并写出自变量的取值范围;
(2)小王家一月份用了115度电,应交电费多少元?
(3)小王家三月份交纳电费49.5元,求小王家三月份用了多少度电?
练习1-1为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量/t 单价/(元/t)
不大于10t部分 1.5
大于10t且不大于mt部分20≤m≤50 2
大于mt部分 3
(1)若某用户六月份用水量为18t,求其应缴纳的水费;
(2)记该用户六月份用水量为xt,缴纳水费y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40t,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
练习1-2某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页1元计费,但需按月付一定数额的承包费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的承包费是 元.
(2)当每月复印 页时,两复印社实际收费相同.
(3)如果每月复印页在250页左右时,应选择哪一个复印社?请简单说明理由.
练习1-3为缓解油价上涨给出租车待业带来的成本压力,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 收费标准
调价前 调价后
不超过3km的部分 起步价6元 起步价a元
超过3km不超出6km的部分 每公里2.1元 每公里b元
超出6km的部分
每公里c元
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
①填空:a= ,b= ,c= .
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.
练习1-4客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,这个函数的图象如图所示.
(1)求y关于x的函数表达式;
(2)求旅客最多可免费携带行李的质量.
时间优化问题
【经典例题2】小碚向某校食堂王经理建议食堂就餐情况,经调查发现就餐时,有520人排队吃饭就餐,就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加,食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12人,每个打饭窗口1每分钟打饭菜10人.已知食堂的前a分钟只开放了两个打饭窗口;某一天食堂排队等候的学生数y(人)与打饭菜时间x(分钟)的关系如图所示.
(1)求a的值;
(2)求排队到第16分钟时,食堂排队等候打饭菜的学生人数;
(3)若要在开始打饭菜后8分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃,那么小碚应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口?
练习2-1为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时?
练习2-2如图1是一个由两个圆柱形构成的容器,最下面的圆柱形底面半径R1=8m.匀速地向空容器内注水,水面高度h(单位:米)与时间t(单位:小时)的关系如图2所示.
(1)求水面高度h与时间t的函数关系式;
(2)求注水的速度(单位:立方米每小时),并求容器内水的体积V与注水时间t的函数关系式;
(3)求上面圆柱的底面半径(壁厚忽略不计).
练习2-3一个容积为200升的水箱,安装有A、B两个水管,加水过程中A水管始终打开,B水管可随时打开或关闭,两水管匀速为水箱加水,且水流速度为定值,当水箱加满时,加水过程结束.
(1)如图是某次加水过程中水箱中水量y(升)与时间x(分)之间的函数图象.
①分别求A、B两水管的水流速度.
②求y与x的函数关系式,
(2)当水箱中无水时,13分钟将水箱加满,求A水管打开后几分钟打开B水管.
练习2-4实验室里,水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计).现三个容器中,只有甲中有水,水位高2cm,如图①所示.若每分钟同时向乙、丙容器中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.
(1)乙、丙两容器的底面积之比为 .
(2)图②中a的值为 ,b的值为 .
(3)注水多少分钟后,乙比甲的水位高2cm?
练习2-5如图所示的是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图Z12-6-2所示.
(图1) (图2)
(1)若乙槽底面积为48平方厘米(壁厚不计),则乙槽中铁块的体积是__cm3;
(2)若乙槽中铁块的体积为98 cm3(壁厚不计),则甲槽底面积是____cm2.
其它问题
【经典例题3】根据国家颁布的“养老保险执行标准”绘制出我市行政事业人员的养老保险个人月缴费y(元)随个人月工资x(元)变化的图象如图~所示,请你根据图象解答下面的问题:
(1)教数学的张老师是中学一级教师,月工资是1568元,张老师每月应缴纳养老保险多少元?
(2)教英语的陈老师是位高级教师,他每月要缴纳养老保险140.21元,求陈老师的每月工资是多少元?
练习3-1(2020?陕西)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式;
(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?
练习3-2已知贺兰山山区的平均气温与该山区的海拔高度的关系见下表:
海拔高度(米) 0 100 200 300 400 500 …
平均气温(℃) 22 21.5 21 20.5 20 19.5 …
(1)平均气温y(℃)是海拔高度x(米)的什么函数?写出y与x之间的函数关系式.
(2)若某种植物适宜生长在18℃~20℃(包括18℃,也包括20℃)的山区,请问该植物适宜种植在海拔为多少米的山区?
练习3-3(2020·广东高州·)空气中传播的速度与气温之间的关系式为;当时,某人看到烟花燃放后才听到声音,则此人与燃放烟花所在地的距离为_________.
练习3-4药品研究所开发一种抗菌素新药,经过多年的动物实验之后,首次用于临床人体试验,测得成人服药后血液中药物浓度(微克/毫升)与服药后时间(时)之间的函数关系如图所示,下列说法正确的是( )
A.当,随增大而减小
B.当,随增大而增大
C.若点和点都在函数图象上,则
D.若血液中药物浓度达到6微克/毫升及以上浓度为有效治疗,则当为有效治疗时间
一次函数应用题-其它费用
【经典例题1】某市电力公司采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.55元计算费用,每月用电超过100度时,超过部分按每度0.60元计算.
(1)设每月用电x度时,应交电费y元,写出y与x之间的函数关系式,并写出自变量的取值范围;
(2)小王家一月份用了115度电,应交电费多少元?
(3)小王家三月份交纳电费49.5元,求小王家三月份用了多少度电?
【解】:(1)由题意可得,
当0<x≤100时,y=0.55x,
当x>100时,y=0.55×100+(x﹣100)×0.6=0.6x﹣5,
由上可得,y与x之间的函数关系式是y=;
(2)当x=115时,y=0.6×115﹣5=64(元),
答:小王家一月份用了115度电,应交电费64元;
(3)∵100×0.55=55>49.5,
∴小王家三月份用电在100度以内,
当y=49.5时,49.5=0.55x,
解得,x=90,
答:小王家三月份用了90度电.
练习1-1为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量/t 单价/(元/t)
不大于10t部分 1.5
大于10t且不大于mt部分20≤m≤50 2
大于mt部分 3
(1)若某用户六月份用水量为18t,求其应缴纳的水费;
(2)记该用户六月份用水量为xt,缴纳水费y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40t,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
【解析】(1)六月份应缴纳的水费为:1.5×10+2×8=31(元);
(2)当0≤x≤10时,y=1.5x,
当10<x≤m时,y=10×1.5+2(x﹣10)=2x﹣5,
当x>m时,y=15+2(m﹣10)+3(x﹣m)=3x﹣m﹣5;
(3)①若所付费用在第2个阶段,40≤m且20≤m≤50,即40≤m≤50时,y=2×40﹣5=75元,满足条件,
②若所付费用到了第3个阶段,y=3×40﹣m﹣5=115﹣m,则70≤115﹣m≤90,
解得:25≤m≤45,
结合①可得25≤m≤45,
综上得,25≤m≤50.
练习1-2某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页1元计费,但需按月付一定数额的承包费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的承包费是 元.
(2)当每月复印 页时,两复印社实际收费相同.
(3)如果每月复印页在250页左右时,应选择哪一个复印社?请简单说明理由.
【解析】(1)由图可知,x=0时,y=18,
所以,乙复印社要求客户每月支付的承包费是18元;
(2)∵两函数图象的交点为(150,30),
∴当每月复印150页时,两复印社实际收费相同;
(3)选择乙.
理由是:当复印页少于150页时,甲的收费较低,
当复印页等于150页时,两复印社收费相同,
当复印页超过150页时,乙的收费较低,
∵250>150,
∴当复印页超过150页时,乙的收费较低.
故答案为:(1)18,(2)150.
练习1-3为缓解油价上涨给出租车待业带来的成本压力,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 收费标准
调价前 调价后
不超过3km的部分 起步价6元 起步价a元
超过3km不超出6km的部分 每公里2.1元 每公里b元
超出6km的部分
每公里c元
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
①填空:a= ,b= ,c= .
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.
【解析】①由图可知,a=7元,
b=(11.2﹣7)÷(6﹣3)=1.4元,
c=(13.3﹣11.2)÷(7﹣6)=2.1元;
②由图得,当x>3时,y1与x的关系式是:
y1=6+(x﹣3)×2.1,
整理得,y1=2.1x﹣0.3;
③由图得,当3<x<6时,y2与x的关系式是:
y2=7+(x﹣3)×1.4,
整理得,y2=1.4x+2.8;
所以,当y1=y2时,交点存在,
即,2.1x﹣0.3=1.4x+2.8,
解得,x=,y=9;
所以,函数y1与y2的图象存在交点(,9);
其意义为:当x<时,是方案调价前合算,当x>时,方案调价后合算;
练习1-4客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,这个函数的图象如图所示.
(1)求y关于x的函数表达式;
(2)求旅客最多可免费携带行李的质量.
【答案】(1)(2)
【解析】
(1)根据(30,4)、(40,6)利用待定系数法,即可求出当行李的质量x超过规定时,y与x之间的函数表达式;
(2)令y=0,求出x值,此题得解.
解:(1)设y与x的函数表达式为y=kx+b,
由题意可得:
解得:
∴(x>10);
(2)当y=0,,
∴x=10,
∴旅客最多可免费携带行李的质量为10kg.
【点睛】
本题主要考查求一次函数解析式,熟练掌握利用待定系数法求解函数表达式是解题的关键.
时间优化问题
【经典例题2】小碚向某校食堂王经理建议食堂就餐情况,经调查发现就餐时,有520人排队吃饭就餐,就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加,食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12人,每个打饭窗口1每分钟打饭菜10人.已知食堂的前a分钟只开放了两个打饭窗口;某一天食堂排队等候的学生数y(人)与打饭菜时间x(分钟)的关系如图所示.
(1)求a的值;
(2)求排队到第16分钟时,食堂排队等候打饭菜的学生人数;
(3)若要在开始打饭菜后8分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃,那么小碚应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口?
【解析】(1)由图象知,520+12a﹣2×10a=424,
∴a=12;
(2)设当12≤x≤20时,y与x之间的函数关系式为y=kx+b,
由题意,得,
解得:,
∴y=﹣53x+1060,
当x=16时,y=212,
即排队到第16分钟时,食堂排队等候打饭菜的学生有212人.
(3)设需同时开放n个打饭窗口,
由题意知10n×8≥520+12×8
解得:n≥7.7,
∵n为整数,
∴n最小=8.
答:至少需要同时开放8个打饭窗口.
练习2-1为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时?
【解析】(1)设y与t的函数解析式为y=kt+b,
,
解得,,
即y与t的函数关系式是y=140t+100,
同时打开甲、乙两个进水口的注水速度是:(380﹣100)÷2=140(m3/h);
(2)∵单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.
∴甲进水口进水的速度是乙进水口进水速度的,
∵同时打开甲、乙两个进水口的注水速度是140m3/h,
∴甲进水口的进水速度为:140÷(+1)×=60(m3/h),
480÷60=8(h),
即单独打开甲进水口注满游泳池需8h.
练习2-2如图1是一个由两个圆柱形构成的容器,最下面的圆柱形底面半径R1=8m.匀速地向空容器内注水,水面高度h(单位:米)与时间t(单位:小时)的关系如图2所示.
(1)求水面高度h与时间t的函数关系式;
(2)求注水的速度(单位:立方米每小时),并求容器内水的体积V与注水时间t的函数关系式;
(3)求上面圆柱的底面半径(壁厚忽略不计).
【解析】(1)当0≤t≤1时,设水面高度h与时间t的函数关系式:h=kt,且过(1,1)
∴1=k
∴当0≤t≤1时,设水面高度h与时间t的函数关系式:h=t
当1<t≤2时,设水面高度h与时间t的函数关系式:h=mt+n,且过(1,1),(2,5)
∴
解得:
∴当1<t≤2时,设水面高度h与时间t的函数关系式:h=4t﹣3
(2)由图2可知,注满下面圆柱所花的时间是1小时,下面圆柱的高度是1米,
设注水的速度为x立方米/每小时,
∴π×82×1=1×x
∴x=64π
∴注水的速度为64π立方米/每小时,
∴容器内水的体积V与注水时间t的函数关系式:V=64πt
(3)设上面圆柱的底面半径为ym
∵π×y2×(5﹣1)=64π×1
∴y=4
∴上面圆柱的底面半径为4m
练习2-3一个容积为200升的水箱,安装有A、B两个水管,加水过程中A水管始终打开,B水管可随时打开或关闭,两水管匀速为水箱加水,且水流速度为定值,当水箱加满时,加水过程结束.
(1)如图是某次加水过程中水箱中水量y(升)与时间x(分)之间的函数图象.
①分别求A、B两水管的水流速度.
②求y与x的函数关系式,
(2)当水箱中无水时,13分钟将水箱加满,求A水管打开后几分钟打开B水管.
【解析】(1)①A水管的水流速度为:40÷8=5(升/分),
B水管的水流速度为:(200﹣40﹣8×5)÷(16﹣8)=160÷8=15(升/分);
②根据题意得
当0≤x≤8时,y=5x;
当8<x≤16时,y=40+20(x﹣8)=20x﹣120.
(2)设先打开A水管a分钟后再打开B水管,
两水管共13分钟将水箱加满,
∴5a+(5+15)(13﹣a)=200,
解得a=4.
即A水管打开4几分钟打开B水管,共13分钟将水箱加满.
练习2-4实验室里,水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计).现三个容器中,只有甲中有水,水位高2cm,如图①所示.若每分钟同时向乙、丙容器中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.
(1)乙、丙两容器的底面积之比为 .
(2)图②中a的值为 ,b的值为 .
(3)注水多少分钟后,乙比甲的水位高2cm?
【解析】(1)观察图象可知:乙、丙两容器的底面积之比为3:1.
故答案为3:1.
(2)∵乙、丙两容器的底面积之比为3:1,丙容器注入2分钟到达6cm,
∴乙容器的水位达到6cm所需时间为:2+2=4(min),
b=(10﹣2+10×3+10)÷6=8(min).
故答案为:4;8.
(3)①当2≤x≤4时,设乙容器水位高度h与时间t的函数关系式为h=kt+b(k≠0),
∵图象经过(2,2)、(4,6)两点,
∴,解得,
∴h=2t﹣2(2≤x≤4).
当h=4时,则2t﹣2=4,解得t=3;
②设t分钟后,甲容器水位为4cm,根据题意得
2+6(t﹣4)=4,
解得.
答:注水3分钟或分钟后,乙比甲的水位高2cm.
练习2-5如图所示的是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图Z12-6-2所示.
(图1) (图2)
(1)若乙槽底面积为48平方厘米(壁厚不计),则乙槽中铁块的体积是__cm3;
(2)若乙槽中铁块的体积为98 cm3(壁厚不计),则甲槽底面积是____cm2.
【解析】(1)由图象知:当水槽中没有没过铁块时4分钟水面上升了12cm,
即1分钟上升3cm,当水面没过铁块时,2分钟上升了5cm,
即1分钟上升2.5cm,
设铁块的底面积为a cm2,则乙水槽中没有没过铁块时每分钟进入水体积分别为:2.5×48cm3,没过铁块时每分钟进入水体积为3×(48-a)cm3,
∴1×3×(48-a)=1×2.5×48,解得a=8,
∴铁块的体积为:8×14=112(cm3);
(2)∵铁块的底面积为98÷14=7(cm2),设乙水槽底面积为b,根据乙水槽中没有没过铁块时每分钟进入水体积与没过铁块时每分钟进入水体积相等,得为1×3×(b-7)=1×2.5×b,解得b=42,
乙水槽每分钟进水105cm3,甲水槽每分钟降低2cm,甲水槽底面积为105÷2=52.5 cm2.
其它问题
【经典例题3】根据国家颁布的“养老保险执行标准”绘制出我市行政事业人员的养老保险个人月缴费y(元)随个人月工资x(元)变化的图象如图~所示,请你根据图象解答下面的问题:
(1)教数学的张老师是中学一级教师,月工资是1568元,张老师每月应缴纳养老保险多少元?
(2)教英语的陈老师是位高级教师,他每月要缴纳养老保险140.21元,求陈老师的每月工资是多少元?
【解析】(1)由题意,设y=kx+b(x≥557).
∵(557,38.99),(1986,139.02)在此函数的图象上,
∴,
解得.
∴y=0.07x.
当x=1568时,y=0.07×1568=109.76.
故张老师每月应缴纳养老保险109.76元;
(2)∵y=0.07x,
∴当y=140.21时,0.07x=140.21,
解得x=2003.
故陈老师的每月工资是2003元.
练习3-1(2020?陕西)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式;
(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?
【解析】(1)当0≤x≤15时,设y=kx(k≠0),
则:20=15k,
解得k,
∴y;
当15<x≤60时,设y=k′x+b(k≠0),
则:,
解得,
∴y,
∴;
(2)当y=80时,80,解得x=33,
33﹣15=18(天),
∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.
练习3-2已知贺兰山山区的平均气温与该山区的海拔高度的关系见下表:
海拔高度(米) 0 100 200 300 400 500 …
平均气温(℃) 22 21.5 21 20.5 20 19.5 …
(1)平均气温y(℃)是海拔高度x(米)的什么函数?写出y与x之间的函数关系式.
(2)若某种植物适宜生长在18℃~20℃(包括18℃,也包括20℃)的山区,请问该植物适宜种植在海拔为多少米的山区?
【答案】(1)一次函数,y=x+22(2)植物适宜种在海拔为400米到800米的山区
【解析】
(1)分析数据可知:高度每增加100米,温度下降0.5℃,据此得知函数为一次函数,设一次函数解析式为:,将表中的两组值代入即可得出答案;
(2)取y=18,20,分别求出高度x的值,再回答问题.
解:(1)根据数据可知高度每增加100米,温度下降0.5℃,得出为一次函数;
设此一次函数解析式为:,
将代入解析式,得
,
解得:,
y与x之间的函数关系式为:;
(2)∵中,,
所以随的增大而减小.
当时,,;
当时,,,
所以
即该植物适宜种植在海拔为400米至800米(包括400米和800米)的山区.
【点睛】
此题考查一次函数的应用,正确表示函数关系式是关键.难度不大.
练习3-3(2020·广东高州·)空气中传播的速度与气温之间的关系式为;当时,某人看到烟花燃放后才听到声音,则此人与燃放烟花所在地的距离为_________.
【答案】1721
【解析】
把气温代入函数关系式求出音速,再根据路程=速度×时间计算即可得解.
解:当x=22时,
344.2×5=1721(米).
答:此人与燃放烟花所在地距离是1721米.
故答案为:
【点睛】
本题考查了一次函数的应用.掌握读懂题目信息,已知自变量的值,求相应的函数值是解题的关键.
练习3-4药品研究所开发一种抗菌素新药,经过多年的动物实验之后,首次用于临床人体试验,测得成人服药后血液中药物浓度(微克/毫升)与服药后时间(时)之间的函数关系如图所示,下列说法正确的是( )
A.当,随增大而减小
B.当,随增大而增大
C.若点和点都在函数图象上,则
D.若血液中药物浓度达到6微克/毫升及以上浓度为有效治疗,则当为有效治疗时间
【答案】C
【解析】
结合图像可判断A,B,求出两段函数表达式,即可判断C,再求出当y≥6时的x范围可判断D.
解:A:当,随增大而增大,选项错误;
B:当时,随增大而增大,当时,随增大而减小,选项错误;
C:设当0≤x≤3时,设y=kx,
∴3k=8,解得:k=,
∴y=x,
当3<x≤14时,设y=ax+b,
∴,解得:,
∴;
∴当x=2时,;当x=5时,,,选项正确;
D:y=x中,令y=6,解得:x=,
中,令y=6,解得:x=,
∴当为有效治疗时间,选项错误.
故选:C.
【点睛】
本题主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
同课章节目录
