专题9圆—9.1垂径定理-2021年鲁教版(五四制)九年级数学专题复习训练(word版含答案)
文档属性
| 名称 | 专题9圆—9.1垂径定理-2021年鲁教版(五四制)九年级数学专题复习训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 07:16:18 | ||
图片预览



文档简介
垂径定理
【知识梳理】
1.圆有关的概念:
(1)圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中,定点为圆心,定长为半径.
(2)圆心角:顶点在圆心的角叫做圆心角.
(3)圆周角:顶点在圆上,两边分别与圆还有另一个交点的角叫做圆周角.
(4)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧称为优弧,小于半圆的弧称为劣弧.
(5)弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径.
2.圆的有关的性质:
(1)圆心角、弦和弧三者之间的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦心距中有一组量相等,那么它们所对应的其余各组量分别相等;
(2)垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧;(基本用法图)
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
垂径定理及其推论可概括为:
过圆心
垂直于弦
直径 平分弦 知二推三
平分弦所对的优弧
平分弦所对的劣弧
(3)圆心角定理:圆心角的度数等于它所对弧的度数;
垂径定理:(三种基本图形)
【经典例题1】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为( )
A. B.8 C. D.
【解析】∵OD⊥弦AB,AB=8,
∴AC=AB=×8=4,
设⊙O的半径OA=r,
∴OC=OD-CD=r-2,
在Rt△OAC中,r2=(r-2)2+42,
解得:r=5,
连结BE,如图,
∵OD=5,CD=2,∴OC=3,
∵AE是直径,∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=.
练习1-1如图,AB是⊙O的弦,直径CD交AB于点E,若AE=EB=3,∠C=15°,则OE的长为 .
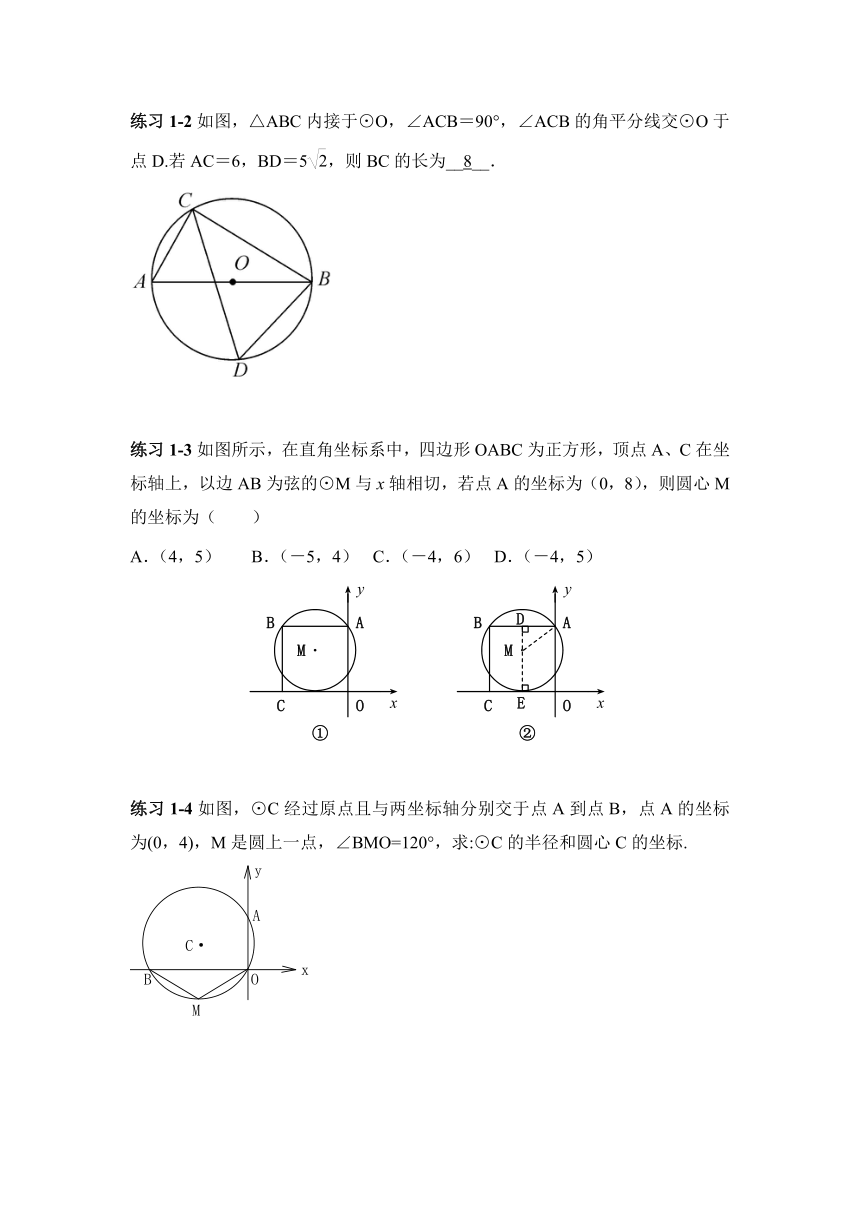
练习1-2如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于点D.若AC=6,BD=5,则BC的长为__8__.
练习1-3如图所示,在直角坐标系中,四边形OABC为正方形,顶点A、C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A的坐标为(0,8),则圆心M的坐标为( )
A.(4,5) B.(-5,4) C.(-4,6) D.(-4,5)
练习1-4如图,⊙C经过原点且与两坐标轴分别交于点A到点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°,求:⊙C的半径和圆心C的坐标.
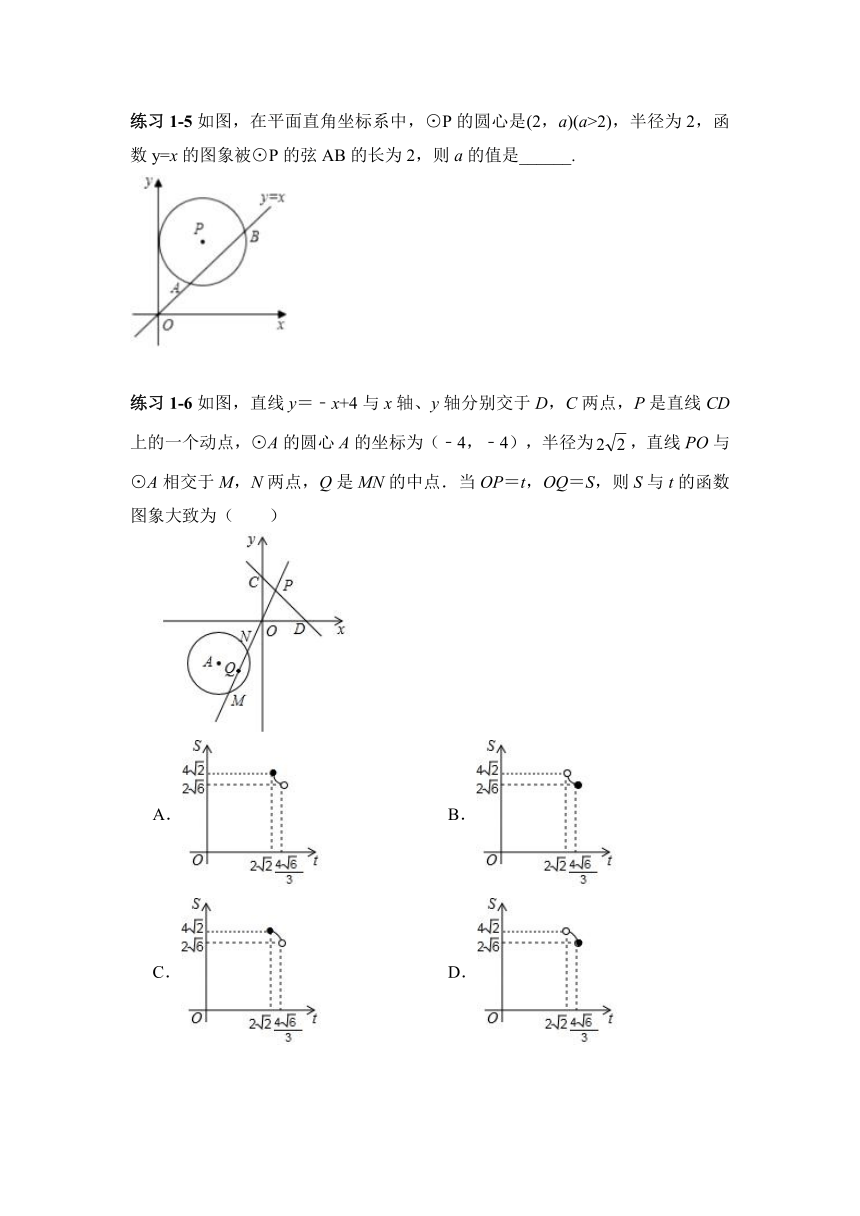
练习1-5如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P的弦AB的长为2,则a的值是______.
练习1-6如图,直线y=﹣x+4与x轴、y轴分别交于D,C两点,P是直线CD上的一个动点,⊙A的圆心A的坐标为(﹣4,﹣4),半径为,直线PO与⊙A相交于M,N两点,Q是MN的中点.当OP=t,OQ=S,则S与t的函数图象大致为( )
A. B.
C. D.
练习1-7如图,坐标平面上,A、B两点分别为圆P与x轴、y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A、B、C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?( )
A.﹣2 B.﹣2 C.﹣8 D.﹣7
练习1-8(2020?鸡西)在半径为的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP= .
练习1-9(2020?青海)已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB与CD之间的距离为 cm.
练习1-10如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
练习1-11如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为点E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为________.
垂径定理应用
【经典例题1】木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.
(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为 .
【解析】(1)如图1,连接OC、OA,作AD⊥OC,垂足为D.则OD=r﹣8
在Rt△AOD中,r2=(r﹣8)2+122
解得:r=13;
答:该圆的半径r为13;
(2)①如图2,易知,0<r≤8时,r=a;
②当r>8时,
如图1:连接OC,连接OA,过点A作AD⊥OC于点D,
∵BC与⊙O相切于点C,
∴OC⊥BC,
则四边形ABCD是矩形,即AD=BC,CD=AB.
在Rt△AOD中,OA2=OD2+AD2,
即:r2=(r﹣8)2+a2,
整理得:r=a2+4.
故答案为:0<r≤8时,r=a;当r>8时,r=a 2+4.
练习2-1图1是某奢侈品牌的香水瓶.从正面看上去(如图2),它可以近似看作⊙O割去两个弓形后余下的部分与矩形ABCD组合而成的图形(点B、C在⊙O上),其中BC∥EF;从侧面看,它是扁平的,厚度为1.3cm.
(1)已知⊙O的半径为2.6cm,BC=2cm,AB=3.02cm,EF=3.12cm,求香水瓶的高度h.
(2)用一张长22cm、宽19cm的矩形硬纸板按照如图3进行裁剪,将实线部分折叠制作成一个底面积为SMNPQ=9cm2的有盖盒子(接缝处忽略不计).请你计算这个盒子的高度,并且判断上述香水瓶能否装入这个盒子里.
练习2-2如图1是一个用铁丝围成的篮筐,我们来仿制一个类似的柱体形篮筐.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
【经典例题3】如图,AB是⊙O的直径,AB=6,OD⊥AB,弧BC为30°,P是直径AB上的点,则PD+PC的最小值是__.?
答案:
练习3-1如图,AB是⊙O的直径,AB=8,弧AB=2弧AD=6弧AC,M是AB上一动点,则CM+DM的最小值是___.?
A.8 B.6 C.2+ D.
答案:D
练习3-2如图,CD是⊙O的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当CD=6时,AP+BP的最小值为_____.
答案:
练习3-3如图 6,AB 是⊙O 的直径,AB=8,点 M 在⊙O 上,∠MAB=20°,N 是弧 MB 的中点,P 是直径 AB 上的一动点,若 MN=1,则△PMN 周长的最小值为( ).
A.4 B.5 C.6 D.7
练习3-4如图,AB为☉O的直径,BC,CD是☉O的切线,切点分别为点B,D,点E为线段OB上的一个动点,连接OD,CE,DE,已知AB=2,BC=2,当CE+DE的值最小时,则的值为( )
B. C. D.
【经典例题1】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为( )
A. B.8 C. D.
练习1-1
【解析】如图,连接OA.
∵AE=EB,∴CD⊥AB,
∴弧AD=弧BD,
∴∠BOD=∠AOD=2∠ACD=30°,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∵AE=3,
∴OE=AE?tan60°=,
故选:D.
练习1-2
【解析】连接AD,
∵∠ACB=90°,
∴AB是⊙O的直径.
∵ACB的角平分线交⊙O于D,
∴∠ACD=∠BCD=45°,
∴AD=BD=.
∵AB是⊙O的直径,
∴△ABD是等腰直角三角形,
∴AB=.
∵AC=6,
∴BC=.
故答案为:8.
练习1-3
【解析】过点M作MD⊥AB于D,连接AM,设M的半径为R,
∵四边形OABC为正方形,顶点A,C在坐标轴上,以边AB为弦的M与x轴相切,点A的坐标为(0,8),
∴DA=4,AB=8,DM=8?R,AM=R,
又∵△ADM是直角三角形,
根据勾股定理可得AM2=DM2+AD2,
∴R2=(8?R)2+42,
解得R=5,
∴M(?4,5).
故选D.
练习1-4
【解析】连接AB,OC,
∵∠AOB=90°,
∴AB为C的直径,
∵∠BMO=120°,
∴∠BCO=120°,∠BAO=60°,
∵AC=OC,∠BAO=60°,
∴△AOC是等边三角形,
∴C的半径=OA=4;
过C作CD⊥OB于D,则OD=OB,
∵∠BAO=60°,
∴∠ABO=30°,
∴OD=,CD=BC=×4=2,
∴D点坐标为(?,0),
∴C点坐标为(?,2).
故答案为:r=4,C(?,2).
练习1-5
【解析】过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
∵PE⊥AB,AB=2,半径为2,
∴AE=12AB=1,PA=2,
根据勾股定理得:PE=,
∵点A在直线y=x上,∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴△OCD是等腰直角三角形,∴OC=CD=2,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=,∴PD=×=.
∵⊙P的圆心是(2,a),
∴a=PD+DC=2+.
故答案为:2+.
练习1-6
【解析】连接AO,并延长交直线CD于G,连接AQ,
∵Q是MN的中点.
∴AQ⊥MN,
∵A的坐标为(﹣4,﹣4),
∴直线AO:y=x,AO=4,
∵直线CD:y=﹣x+4,
∴AO⊥CD,
∴∠AQO=∠OGP=90°,
∵∠AOQ=∠POG,
∴∠AOQ∽△POG,
∴,
当x=0时,y=4,当y=0时,x=4,
∴OC=OD=4,
∴OG=CD=2,
∵OP=t,OQ=S,
∴,
S=,
故选项C、D不正确;
当OP=2时,即S=OQ=4,t=2,直线OP过圆心A,此时Q与A重合,此种情况成立,
故选项B不正确;
故选:A.
练习1-7
【解析】连接AC,
由题意得,BC=OB+OC=9,
∵直线L通过P点且与AB垂直,
∴直线L是线段AB的垂直平分线,
∴AC=BC=9,
在Rt△AOC中,AO==2,
∵a<0,
∴a=﹣2,
故选:A.
练习1-8
【解析】作OE⊥AB于E,OF⊥CD于F,连结OD、OB,
则AE=BE=AB=2,DF=CF=CD=2,
如图1,
在Rt△OBE中,∵OB=,BE=2,
∴OE==1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
∴PE=PF=1,
∴PA=PC=1,
∴S△APC==;
如图2,
同理:S△APC==;
如图3,
同理:S△APC==;
故答案为:或或.
练习1-9
【解析】作OE⊥AB于E,延长EO交CD于F,连接OA、OC,如图,
∵AB∥CD,OE⊥AB,
∴OF⊥CD,
∴AE=BE=AB=4cm,CF=DF=CD=3cm,
在Rt△OAE中,OE===3cm,
在Rt△OCF中,OF===4cm,
当点O在AB与CD之间时,如图1,EF=OF+OE=4+3=7cm;
当点O不在AB与CD之间时,如图2,EF=OF﹣OE=4﹣3=1cm;
综上所述,AB与CD之间的距离为1cm或7cm.
故答案为1或7.
练习1-10
【解析】∵四边形OCDB是平行四边形,B(16,0),
∴CD∥OA,CD=OB=16,
过点M作MF⊥CD于点F,则CF=CD=8,
过点C作CE⊥OA于点E,
∵A(20,0),
∴OE=OM﹣ME=OM﹣CF=10﹣8=2.
连接MC,则MC=OA=10,
∴在Rt△CMF中,由勾股定理得MF==6
∴点C的坐标为(2,6)
故答案为:(2,6).
练习1-11
【解析】连接BC,如图,
∵AB是半圆的直径,
∴∠ACB=90°,
在Rt△ABC中,BC=
∵OD⊥AC,
∴AE=CE=AC=4,
在Rt△BCE中,BE=,
∴sinα=.
垂径定理应用
练习2-1
【解析】(1)作OG⊥BC于G,延长GO交EF于H,连接BO、EO.
∵EF∥BC,
∴OH⊥EF,
∴BG=BC,EH=EF
∴GO==2.4;OH==2.08,
∴h=2.4+2.08+3.02=7.5cm.
(2)设盒子的高为xcm.
由题意:(22﹣2x)?=9
解得x=8或12.5(舍弃),
∴MQ=6,MN=1.5
∵2.6×2=5.2<6;1.3<1.5;7.5<8,
∴能装入盒子.
练习2-2
【解析】(1)在Rt△D2EC2中,∵∠D2EC2=90°,EC2=ED2=r,EF⊥C2D2,
∴EH2=r,FH2=r﹣r,
∴d=(r﹣r)=r,
(2)假设CnDn与点E间的距离能等于d,由题意?r=r,
这个方程n没有整数解,
所以假设不成立.
∵r÷r=2+2≈4.8,
∴直角三角形△C2ED2最多分成5份,
∴n=6,此时CnDn与点E间的距离=r﹣4×r=r.
【经典例题3】如图,AB是⊙O的直径,AB=6,OD⊥AB,弧BC为30°,P是直径AB上的点,则PD+PC的最小值是__.?
答案:
练习3-1如图,AB是⊙O的直径,AB=8,弧AB=2弧AD=6弧AC,M是AB上一动点,则CM+DM的最小值是___.?
A.8 B.6 C.2+ D.
答案:D
练习3-2如图,CD是⊙O的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当CD=6时,AP+BP的最小值为_____.
答案:
练习3-3如图 6,AB 是⊙O 的直径,AB=8,点 M 在⊙O 上,∠MAB=20°,N 是弧 MB 的中点,P 是直径 AB 上的一动点,若 MN=1,则△PMN 周长的最小值为( ).
A.4 B.5 C.6 D.7
【解析】作 N 关于 AB 的对称点 N′,连接 MN′,NN′,ON′,ON.
∵N 关于 AB 的对称点 N′,
∴MN′与 AB 的交点 P′即为△PMN 周长的最小时的点,
∵N 是弧 MB 的中点,
∴∠A=∠NOB=∠MON=20°,
∴∠MON′=60°,
∴△MON′为等边三角形,
∴MN′=OM=4,
∴△PMN 周长的最小值为 4+1=5. 故选 B.
练习3-4如图,AB为☉O的直径,BC,CD是☉O的切线,切点分别为点B,D,点E为线段OB上的一个动点,连接OD,CE,DE,已知AB=2,BC=2,当CE+DE的值最小时,则的值为( )
B. C. D.
答案:A
【知识梳理】
1.圆有关的概念:
(1)圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中,定点为圆心,定长为半径.
(2)圆心角:顶点在圆心的角叫做圆心角.
(3)圆周角:顶点在圆上,两边分别与圆还有另一个交点的角叫做圆周角.
(4)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧称为优弧,小于半圆的弧称为劣弧.
(5)弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径.
2.圆的有关的性质:
(1)圆心角、弦和弧三者之间的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦心距中有一组量相等,那么它们所对应的其余各组量分别相等;
(2)垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧;(基本用法图)
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
垂径定理及其推论可概括为:
过圆心
垂直于弦
直径 平分弦 知二推三
平分弦所对的优弧
平分弦所对的劣弧
(3)圆心角定理:圆心角的度数等于它所对弧的度数;
垂径定理:(三种基本图形)
【经典例题1】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为( )
A. B.8 C. D.
【解析】∵OD⊥弦AB,AB=8,
∴AC=AB=×8=4,
设⊙O的半径OA=r,
∴OC=OD-CD=r-2,
在Rt△OAC中,r2=(r-2)2+42,
解得:r=5,
连结BE,如图,
∵OD=5,CD=2,∴OC=3,
∵AE是直径,∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=.
练习1-1如图,AB是⊙O的弦,直径CD交AB于点E,若AE=EB=3,∠C=15°,则OE的长为 .
练习1-2如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于点D.若AC=6,BD=5,则BC的长为__8__.
练习1-3如图所示,在直角坐标系中,四边形OABC为正方形,顶点A、C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A的坐标为(0,8),则圆心M的坐标为( )
A.(4,5) B.(-5,4) C.(-4,6) D.(-4,5)
练习1-4如图,⊙C经过原点且与两坐标轴分别交于点A到点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°,求:⊙C的半径和圆心C的坐标.
练习1-5如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P的弦AB的长为2,则a的值是______.
练习1-6如图,直线y=﹣x+4与x轴、y轴分别交于D,C两点,P是直线CD上的一个动点,⊙A的圆心A的坐标为(﹣4,﹣4),半径为,直线PO与⊙A相交于M,N两点,Q是MN的中点.当OP=t,OQ=S,则S与t的函数图象大致为( )
A. B.
C. D.
练习1-7如图,坐标平面上,A、B两点分别为圆P与x轴、y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A、B、C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?( )
A.﹣2 B.﹣2 C.﹣8 D.﹣7
练习1-8(2020?鸡西)在半径为的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP= .
练习1-9(2020?青海)已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB与CD之间的距离为 cm.
练习1-10如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
练习1-11如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为点E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为________.
垂径定理应用
【经典例题1】木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.
(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为 .
【解析】(1)如图1,连接OC、OA,作AD⊥OC,垂足为D.则OD=r﹣8
在Rt△AOD中,r2=(r﹣8)2+122
解得:r=13;
答:该圆的半径r为13;
(2)①如图2,易知,0<r≤8时,r=a;
②当r>8时,
如图1:连接OC,连接OA,过点A作AD⊥OC于点D,
∵BC与⊙O相切于点C,
∴OC⊥BC,
则四边形ABCD是矩形,即AD=BC,CD=AB.
在Rt△AOD中,OA2=OD2+AD2,
即:r2=(r﹣8)2+a2,
整理得:r=a2+4.
故答案为:0<r≤8时,r=a;当r>8时,r=a 2+4.
练习2-1图1是某奢侈品牌的香水瓶.从正面看上去(如图2),它可以近似看作⊙O割去两个弓形后余下的部分与矩形ABCD组合而成的图形(点B、C在⊙O上),其中BC∥EF;从侧面看,它是扁平的,厚度为1.3cm.
(1)已知⊙O的半径为2.6cm,BC=2cm,AB=3.02cm,EF=3.12cm,求香水瓶的高度h.
(2)用一张长22cm、宽19cm的矩形硬纸板按照如图3进行裁剪,将实线部分折叠制作成一个底面积为SMNPQ=9cm2的有盖盒子(接缝处忽略不计).请你计算这个盒子的高度,并且判断上述香水瓶能否装入这个盒子里.
练习2-2如图1是一个用铁丝围成的篮筐,我们来仿制一个类似的柱体形篮筐.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
【经典例题3】如图,AB是⊙O的直径,AB=6,OD⊥AB,弧BC为30°,P是直径AB上的点,则PD+PC的最小值是__.?
答案:
练习3-1如图,AB是⊙O的直径,AB=8,弧AB=2弧AD=6弧AC,M是AB上一动点,则CM+DM的最小值是___.?
A.8 B.6 C.2+ D.
答案:D
练习3-2如图,CD是⊙O的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当CD=6时,AP+BP的最小值为_____.
答案:
练习3-3如图 6,AB 是⊙O 的直径,AB=8,点 M 在⊙O 上,∠MAB=20°,N 是弧 MB 的中点,P 是直径 AB 上的一动点,若 MN=1,则△PMN 周长的最小值为( ).
A.4 B.5 C.6 D.7
练习3-4如图,AB为☉O的直径,BC,CD是☉O的切线,切点分别为点B,D,点E为线段OB上的一个动点,连接OD,CE,DE,已知AB=2,BC=2,当CE+DE的值最小时,则的值为( )
B. C. D.
【经典例题1】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为( )
A. B.8 C. D.
练习1-1
【解析】如图,连接OA.
∵AE=EB,∴CD⊥AB,
∴弧AD=弧BD,
∴∠BOD=∠AOD=2∠ACD=30°,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∵AE=3,
∴OE=AE?tan60°=,
故选:D.
练习1-2
【解析】连接AD,
∵∠ACB=90°,
∴AB是⊙O的直径.
∵ACB的角平分线交⊙O于D,
∴∠ACD=∠BCD=45°,
∴AD=BD=.
∵AB是⊙O的直径,
∴△ABD是等腰直角三角形,
∴AB=.
∵AC=6,
∴BC=.
故答案为:8.
练习1-3
【解析】过点M作MD⊥AB于D,连接AM,设M的半径为R,
∵四边形OABC为正方形,顶点A,C在坐标轴上,以边AB为弦的M与x轴相切,点A的坐标为(0,8),
∴DA=4,AB=8,DM=8?R,AM=R,
又∵△ADM是直角三角形,
根据勾股定理可得AM2=DM2+AD2,
∴R2=(8?R)2+42,
解得R=5,
∴M(?4,5).
故选D.
练习1-4
【解析】连接AB,OC,
∵∠AOB=90°,
∴AB为C的直径,
∵∠BMO=120°,
∴∠BCO=120°,∠BAO=60°,
∵AC=OC,∠BAO=60°,
∴△AOC是等边三角形,
∴C的半径=OA=4;
过C作CD⊥OB于D,则OD=OB,
∵∠BAO=60°,
∴∠ABO=30°,
∴OD=,CD=BC=×4=2,
∴D点坐标为(?,0),
∴C点坐标为(?,2).
故答案为:r=4,C(?,2).
练习1-5
【解析】过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
∵PE⊥AB,AB=2,半径为2,
∴AE=12AB=1,PA=2,
根据勾股定理得:PE=,
∵点A在直线y=x上,∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴△OCD是等腰直角三角形,∴OC=CD=2,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=,∴PD=×=.
∵⊙P的圆心是(2,a),
∴a=PD+DC=2+.
故答案为:2+.
练习1-6
【解析】连接AO,并延长交直线CD于G,连接AQ,
∵Q是MN的中点.
∴AQ⊥MN,
∵A的坐标为(﹣4,﹣4),
∴直线AO:y=x,AO=4,
∵直线CD:y=﹣x+4,
∴AO⊥CD,
∴∠AQO=∠OGP=90°,
∵∠AOQ=∠POG,
∴∠AOQ∽△POG,
∴,
当x=0时,y=4,当y=0时,x=4,
∴OC=OD=4,
∴OG=CD=2,
∵OP=t,OQ=S,
∴,
S=,
故选项C、D不正确;
当OP=2时,即S=OQ=4,t=2,直线OP过圆心A,此时Q与A重合,此种情况成立,
故选项B不正确;
故选:A.
练习1-7
【解析】连接AC,
由题意得,BC=OB+OC=9,
∵直线L通过P点且与AB垂直,
∴直线L是线段AB的垂直平分线,
∴AC=BC=9,
在Rt△AOC中,AO==2,
∵a<0,
∴a=﹣2,
故选:A.
练习1-8
【解析】作OE⊥AB于E,OF⊥CD于F,连结OD、OB,
则AE=BE=AB=2,DF=CF=CD=2,
如图1,
在Rt△OBE中,∵OB=,BE=2,
∴OE==1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
∴PE=PF=1,
∴PA=PC=1,
∴S△APC==;
如图2,
同理:S△APC==;
如图3,
同理:S△APC==;
故答案为:或或.
练习1-9
【解析】作OE⊥AB于E,延长EO交CD于F,连接OA、OC,如图,
∵AB∥CD,OE⊥AB,
∴OF⊥CD,
∴AE=BE=AB=4cm,CF=DF=CD=3cm,
在Rt△OAE中,OE===3cm,
在Rt△OCF中,OF===4cm,
当点O在AB与CD之间时,如图1,EF=OF+OE=4+3=7cm;
当点O不在AB与CD之间时,如图2,EF=OF﹣OE=4﹣3=1cm;
综上所述,AB与CD之间的距离为1cm或7cm.
故答案为1或7.
练习1-10
【解析】∵四边形OCDB是平行四边形,B(16,0),
∴CD∥OA,CD=OB=16,
过点M作MF⊥CD于点F,则CF=CD=8,
过点C作CE⊥OA于点E,
∵A(20,0),
∴OE=OM﹣ME=OM﹣CF=10﹣8=2.
连接MC,则MC=OA=10,
∴在Rt△CMF中,由勾股定理得MF==6
∴点C的坐标为(2,6)
故答案为:(2,6).
练习1-11
【解析】连接BC,如图,
∵AB是半圆的直径,
∴∠ACB=90°,
在Rt△ABC中,BC=
∵OD⊥AC,
∴AE=CE=AC=4,
在Rt△BCE中,BE=,
∴sinα=.
垂径定理应用
练习2-1
【解析】(1)作OG⊥BC于G,延长GO交EF于H,连接BO、EO.
∵EF∥BC,
∴OH⊥EF,
∴BG=BC,EH=EF
∴GO==2.4;OH==2.08,
∴h=2.4+2.08+3.02=7.5cm.
(2)设盒子的高为xcm.
由题意:(22﹣2x)?=9
解得x=8或12.5(舍弃),
∴MQ=6,MN=1.5
∵2.6×2=5.2<6;1.3<1.5;7.5<8,
∴能装入盒子.
练习2-2
【解析】(1)在Rt△D2EC2中,∵∠D2EC2=90°,EC2=ED2=r,EF⊥C2D2,
∴EH2=r,FH2=r﹣r,
∴d=(r﹣r)=r,
(2)假设CnDn与点E间的距离能等于d,由题意?r=r,
这个方程n没有整数解,
所以假设不成立.
∵r÷r=2+2≈4.8,
∴直角三角形△C2ED2最多分成5份,
∴n=6,此时CnDn与点E间的距离=r﹣4×r=r.
【经典例题3】如图,AB是⊙O的直径,AB=6,OD⊥AB,弧BC为30°,P是直径AB上的点,则PD+PC的最小值是__.?
答案:
练习3-1如图,AB是⊙O的直径,AB=8,弧AB=2弧AD=6弧AC,M是AB上一动点,则CM+DM的最小值是___.?
A.8 B.6 C.2+ D.
答案:D
练习3-2如图,CD是⊙O的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当CD=6时,AP+BP的最小值为_____.
答案:
练习3-3如图 6,AB 是⊙O 的直径,AB=8,点 M 在⊙O 上,∠MAB=20°,N 是弧 MB 的中点,P 是直径 AB 上的一动点,若 MN=1,则△PMN 周长的最小值为( ).
A.4 B.5 C.6 D.7
【解析】作 N 关于 AB 的对称点 N′,连接 MN′,NN′,ON′,ON.
∵N 关于 AB 的对称点 N′,
∴MN′与 AB 的交点 P′即为△PMN 周长的最小时的点,
∵N 是弧 MB 的中点,
∴∠A=∠NOB=∠MON=20°,
∴∠MON′=60°,
∴△MON′为等边三角形,
∴MN′=OM=4,
∴△PMN 周长的最小值为 4+1=5. 故选 B.
练习3-4如图,AB为☉O的直径,BC,CD是☉O的切线,切点分别为点B,D,点E为线段OB上的一个动点,连接OD,CE,DE,已知AB=2,BC=2,当CE+DE的值最小时,则的值为( )
B. C. D.
答案:A
同课章节目录
